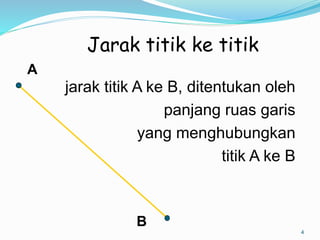
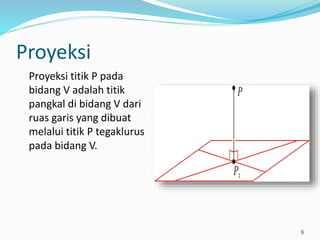
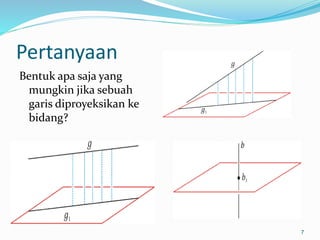
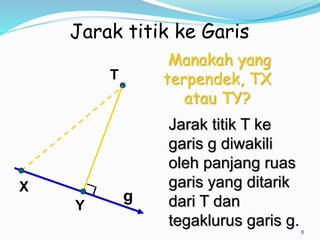
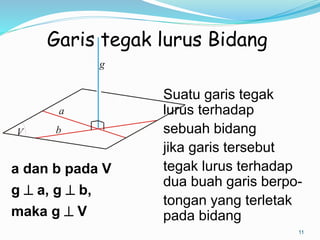
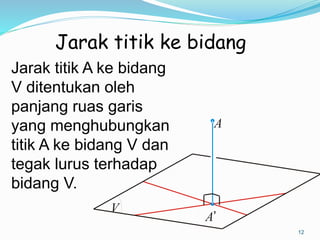
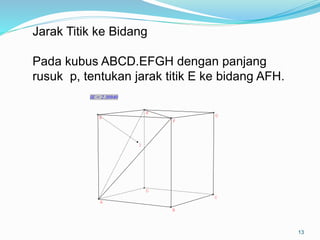
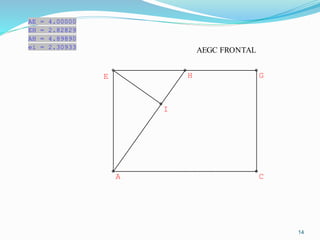
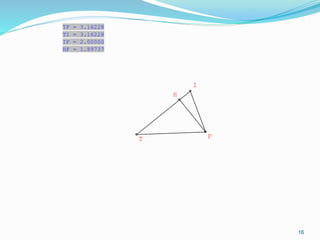
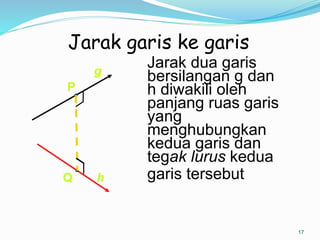
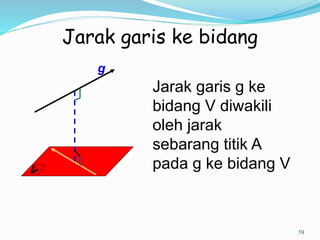
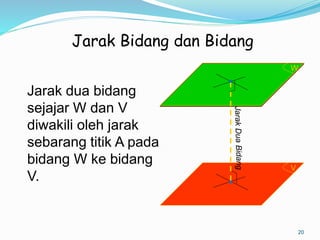
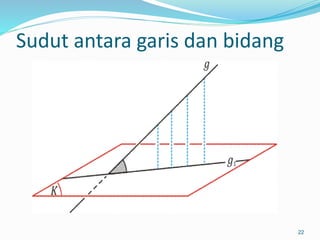
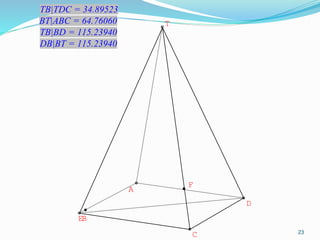
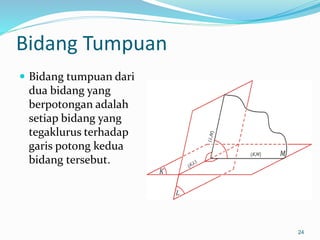
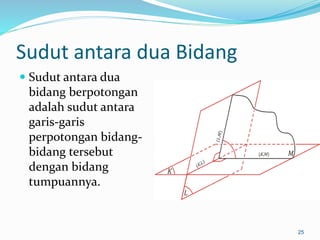
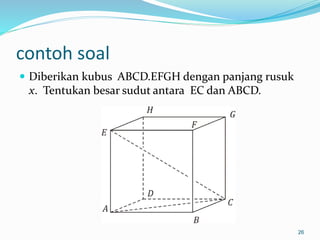
Dokumen ini membahas mengenai prinsip dasar dalam menentukan jarak dan sudut antara berbagai elemen geometri dalam ruang tiga dimensi, seperti titik, garis, dan bidang. Meliputi metode perhitungan jarak titik ke titik, garis ke garis, serta aspek proyeksi, termasuk penerapan teorema Pythagoras dan trigonometri. Terdapat juga contoh soal untuk praktik dalam memahami konsep-konsep tersebut.

1. 1
Jarak dan Sudut
Disampaikan pada
Diklat SMA Tahap 1
Di PPPPTK Matematika
14-26 Juni 2012

2. 2
Menentukan
jarak antara unsur-unsur dalam
ruang dimensi tiga

3. 3
Bagaimana menentukan jarak antara:
 titik ke titik
 titik ke garis
 titik ke bidang
 garis ke garis
 garis ke bidang
 bidang ke bidang
Senjata:
T. Pythagoras
Trigonometri
Kesebangunan
…

4. 4
Jarak titik ke titik
jarak titik A ke B, ditentukan oleh
panjang ruas garis
yang menghubungkan
titik A ke B
A
B

5. 5
A
B
C
D
E
F
G
H
AC = 5.65685
FD = 6.92820
Contoh:
Jarak titik A ke C
Jarak titik F ke D

6. Proyeksi
Proyeksi titik P pada
bidang V adalah titik
pangkal di bidang V dari
ruas garis yang dibuat
melalui titik P tegaklurus
pada bidang V.
6

7. Pertanyaan
Bentuk apa saja yang
mungkin jika sebuah
garis diproyeksikan ke
bidang?
7

8. 8
Jarak titik ke Garis
T
g
Jarak titik T ke
garis g diwakili
oleh panjang ruas
garis yang ditarik
dari T dan
tegaklurus garis g.
Y
X
Manakah yang
terpendek, TX
atau TY?

9. 9
A
B
C
D
E
F
G
H
I
J
FI = 2.82843
CJ = 3.65148
G
E
B
I
LUKIS SEGITIGA EBG DALAM BIDANG FRONTAL
Pada kubus ABCD.EFGH, dengan panjang rusuk
p, tentukan:
a. Jarak titik G ke garis BE.
b. Jarak C ke garis GI

10. 10
G
I
C
J
IC = 4.89898
GI = 4.89898
CJ = 3.65148

11. 11
Garis tegak lurus Bidang
Suatu garis tegak
lurus terhadap
sebuah bidang
jika garis tersebut
tegak lurus terhadap
dua buah garis berpo-
tongan yang terletak
pada bidang
a dan b pada V
g  a, g  b,
maka g  V
V
a
b
g

12. 12
Jarak titik ke bidang
Jarak titik A ke bidang
V ditentukan oleh
panjang ruas garis
yang menghubungkan
titik A ke bidang V dan
tegak lurus terhadap
bidang V.
V
A
A’

13. A
B
C
D
E
F
G
H
I
IE = 2.30940
13
Jarak Titik ke Bidang
Pada kubus ABCD.EFGH dengan panjang
rusuk p, tentukan jarak titik E ke bidang AFH.

14. 14
A C
G
E H
I
AE = 4.00000
EH = 2.82829
AH = 4.89890
ei = 2.30933
AEGC FRONTAL

15. A
B
C
D
T
E
F
G
H
AE = 1.89737
FH = 1.89737
15
Pada limas
segiempat T.ABCD,
tentukan jarak A ke
bidang TDC.

16. I
T F
H
TF = 3.16228
TI = 3.16228
IF = 2.00000
HF = 1.89737
16

17. 17
Jarak garis ke garis
Jarak dua garis
bersilangan g dan
h diwakili oleh
panjang ruas garis
yang
menghubungkan
kedua garis dan
tegak lurus kedua
garis tersebut
P
Q
g
h

18. 18
A
B C
D
T
E
F
Jarak AB ke CT diwakili
oleh EF

19. 19
Jarak garis ke bidang
Jarak garis g ke
bidang V diwakili
oleh jarak
sebarang titik A
pada g ke bidang V
g

20. 20
V
W
Jarak Bidang dan Bidang
Jarak dua bidang
sejajar W dan V
diwakili oleh jarak
sebarang titik A pada
bidang W ke bidang
V.
W

21. Sudut antara garis dan bidang
Jika garis g tidak tegak lurus bidang V,
maka sudut antara garis g dan bidang V
adalah sudut lancip yang dibentuk oleh
garis g dan proyeksi garis g pada bidang
V.
21
( , ) ( , ')
g V g g 
   

22. Sudut antara garis dan bidang
22

23. 23
A
B
C
D
T
E
F
TB|TDC = 34.89523
BT|ABC = 64.76060
TB|BD = 115.23940
DB|BT = 115.23940

24. Bidang Tumpuan
 Bidang tumpuan dari
dua bidang yang
berpotongan adalah
setiap bidang yang
tegaklurus terhadap
garis potong kedua
bidang tersebut.
24

25. Sudut antara dua Bidang
 Sudut antara dua
bidang berpotongan
adalah sudut antara
garis-garis
perpotongan bidang-
bidang tersebut
dengan bidang
tumpuannya.
25

26. contoh soal
 Diberikan kubus ABCD.EFGH dengan panjang rusuk
x. Tentukan besar sudut antara EC dan ABCD.
26

27. Soal 0
Tentukan banyak garis lurus yang memotong tiga buah
garis yang saling bersilangan.
27

28. Soal 1.
 Diberikan kubus ABCD.EFGH dengan panjang rusuk 1
satuan. Titik P dan Q berturut-turut merupakan titik
tengah rusuk GC dan GH.
Tentukan jarak F ke bidang BPQE
28

29. Soal 2
 Titik P di pertengahan rusuk BC dan titik Q di
pertengahan rusuk OH pada kubus ABCE.EFGH yang
panjang rusuknya a cm. Jika R merupakan proyeksi Q
pada bidang ABCD, tentukan:
a. panjang PC
b. Panjang PQ
c. sin , jika  sudut antara PQ dengan bidang ABCD
29

30. Sekian dan Terima Kasih
30