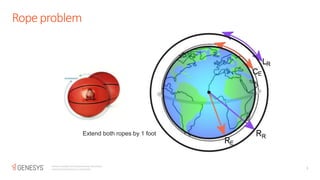
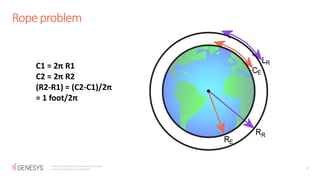
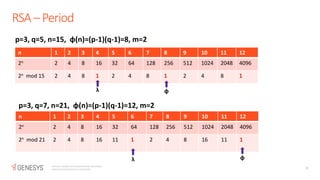
The document discusses the RSA encryption algorithm. It begins by explaining how to generate the public and private keys, including choosing two prime numbers p and q, computing phi(n) as (p-1)(q-1), and selecting the public and private exponents e and d. It then explains how RSA encryption and decryption work using these keys. The document also discusses some ways RSA can be broken, such as with a quantum computer using Shor's algorithm to find the prime factors of n through periodicity. It provides examples to illustrate RSA key generation and encryption/decryption.

1. DeepDiveintoRSA

2. Astory
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited. 2
Bjarne Stroustrup Linus Torvalds
Dennis Ritchie

3. Ropeproblem
3
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
Extend both ropes by 1 foot

4. Ropeproblem
4
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
C1 = 2π R1
C2 = 2π R2
(R2-R1) = (C2-C1)/2π
= 1 foot/2π

5. Ropeproblem
5
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

6. RSA– Keygeneration
◦ Choose two primes p and q of approximately equal size so that their product n = pq is
of the required length (1024, 2048…).
◦ Compute φ(n) = (p-1)(q-1).
◦ Choose a public exponent e, 1 < e < φ(n), which is coprime to φ(n), that is, gcd(e,
φ(n))=1. coprime {4, 9}, {8, 21}
◦ Compute a private exponent d that satisfies the congruence ed ≡ 1 (mod φ(n)).
ed = 1+φ(n)*k
◦ Make the public key (n, e) available to others. Keep the private values d, p, q, and
φ(n) secret.
6
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

7. RSA– Encryption
◦ Encryption c = me mod n, 1 < m < n-1
◦ Decryption m = cd mod n
◦ m = RSAPUBLIC(RSAPRIVATE(m))
7
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

8. RSA– Period
8
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
p=3, q=5, n=15, φ(n)=(p-1)(q-1)=8, m=2
n 1 2 3 4 5 6 7 8 9 10 11 12
2n 2 4 8 16 32 64 128 256 512 1024 2048 4096
2n mod 15 2 4 8 2 4 8 2 4 8
p=3, q=7, n=21, φ(n)=(p-1)(q-1)=12, m=2
n 1 2 3 4 5 6 7 8 9 10 11 12
2n 2 4 8 16 32 64 128 256 512 1024 2048 4096
2n mod 21 2 4 8 16 11 2 4 8 16 11
φ
φλ
λ

9. RSA -φ(n)
◦ φ(n) - how many positive integers less than n and coprime to n.
E.g. φ(12)=4 as the 4 integers {1,5,7,11}
◦ For any prime p, φ(p)=p−1, since all numbers less than p are coprime to it.
E.g. φ(7)=6 as the 6 integers {1,2,3,4,5,6}
◦ If m and n are coprime, then φ(m)φ(n)=φ(mn).
Now we understand what is ‘Compute φ(n) = (p-1)(q-1)’
9
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

10. RSA- Pattern
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
p=7, φ(p)=6, m=2
i 1 2 3 4 5 6
i*m 2 4 6 8 10 12
i*m mod p 2 4 6 3 5
p=12, φ(p)=4, m=5 (m coprime to p)
i 1 5 7 11
i*m 5 25 35 55
i*m mod p 5 1 11

11. RSA- Fermat’sLittleTheorem
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
p=7, φ(p)=6, m=2
i 1 2 3 4 5 6
i*m 2 4 6 8 10 12
i*m mod p 2 4 6 3 5
m*2m*3m…*(p-1)m ≡ 1*2*3…*(p-1)(mod p) =>
(mp-1)*1*2*3…*(p-1) ≡ 1*2*3…*(p-1)(mod p) =>
mp-1 ≡ 1 (mod p) => mφ(n) ≡ 1 (mod p)

12. RSA -Proof
◦ Encryption c = me mod n
◦ Decryption m = cd mod n
◦ ed = 1+kφ(n)
◦ cd ≡ med
≡ m1+kφ(n)
≡ m.(mφ(n))k
≡ m.1k ,since mφ(n) ≡ 1 (mod n)
≡ m (mod n).
12
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

13. RSA -Breaking
◦ me mod n with small e, m is not secure (if me < n)
◦ Today almost in all public keys (e,n), e=3, 17 and 65537, why?
c1 = m3 mod n1, c2 = m3 mod n2, c3 = m3 mod n3
m can be revealed by Chinese remainder theorem
c1* c2* c3 = m3 mod (n1* n2* n3) = m3 (if m3 < n1* n2* n3 )
◦ RSA without padding is vulnerable
13
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

14. RSA -Breaking
◦ Brute force - Check all odd numbers starting below the square root of n.
◦ Euclidean Algorithm – if you can find two n1 and n2 have a common factor. In the real
world, about two out of 1000 secure web sites RSA moduli do have common factors,
and thus are susceptible to cracking (http://eprint.iacr.org/2012/064.pdf)
◦ Shor's algorithm -Key is to find ‘Period’ which requires a quantum computer
◦ https://en.wikipedia.org/wiki/RSA_Factoring_Challenge
14
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

15. RSA -Quantumsuperposition
15
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

16. RSA -Quantumentanglement
16
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.

17. RSA -Quantumcomputer
◦ Qubits – Superposition and Entanglement (n qubits can represent 2n state)
◦ Qubits – State is described in probability amplitude (0.5, 0.866…), (0.5, -0.866…)
17
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
Bloch sphere

18. RSA -Shor'salgorithm
18
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.
Quantum Fourier Transform analogy

19. Questions?
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited. 19

20. Copyright ©2017 Genesys.
2001 Junipero Serra Blvd., Daly City, CA 94014
All Rights reserved. Genesys and the Genesys logo are registered trademarks of Genesys. All other company names and logos may be registered
trademarks or trademarks of their respective companies.
Thank You
Visit www.genesys.com or call +1.855.821.0932 for more information
Genesys confidential and proprietary information.
Unauthorized disclosure is prohibited.