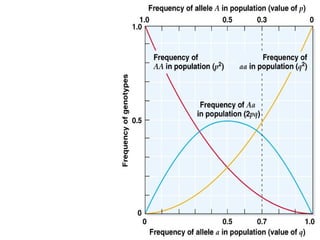
Population genetics studies how allele and gene frequencies change over time in a population. It examines genotypic and allelic frequencies to determine how common certain combinations and individual alleles are. The Hardy-Weinberg principle states that allele and genotype frequencies will remain in equilibrium in a large, randomly mating population with no evolutionary influences. Factors like mutation, genetic drift, migration and selection can cause frequencies to change from this equilibrium over time. Population variation is quantified by measuring heterozygosity and the proportion of polymorphic loci between individuals.

1. Population Genetics
By:
Quidez Dean Adrian

2. Mendelain populations and the gene pool
Inheritance and maintenance of alleles and genes
within a population of randomly breeding individuals
Study of how often or frequent genes and/or alleles
appear in the population
Genotypic frequencies – how often do certain allelic
combinations appear
Allelic frequencies - how often does an individual allele
appear

3. Genotypic frequencies
BB
frequency a particular
genotype appears
(combination of alleles)
for moths at right
Bb
out of 497 moths collected
BB appears 452 times
Bb appears 43 times
bb appears 2 times
Bb
Frequencies
BB 452 ÷ 492 = 0.909
Bb 43 ÷ 492 = 0.087
bb 2 ÷ 492 = 0.004
Total 1.000 bb

4. What about alleles that do show simple dominant -
recessive relationship?
How does genotypic frequency really demonstrate
flux or change in frequencies of the dominant
allele?
What if there are multiple alleles?
Allelic frequencies

5. Allelic frequency
BB
Allelic frequency = Number
of copies of a given allele
divided by sum of counts of
all alleles Bb
BB appears 452 times
Bb appears 43 times
bb appears 2 times
492 moths Bb
994 alleles
Frequencies
B (904 + 43) ÷ 994 = 0.953
b (43 + 4) ÷ 994 = 0.047 bb
Total 1.000

6. Can also calculate it from the genotypic frequencies
BB was 0.909
Bb was 0.087
bb was 0.004
Therefore frequency of B = Frequency of BB + ½
frequency of Bb
f(B) = .909 + ½ 0.087 = .909 + .0435 = .9525
F(b) = 0.004 + ½ 0.087 = 0.004 + 0.0435 = 0.047
What about multiple alleles?

7. Genotype Number
A1A1 4
A1A2 41
A2A2 84
A1A3 25
A2A3 88
A3A3 32
Total 274
f(A1) = Total number of A1 in population divided by total
number of alleles

8. Genotype Number
A1A1 4
A1A2 41
A2A2 84
A1A3 25
A2A3 88
A3A3 32
Total 274
f(A1) = Total number of A1 in population divided by total
number of alleles

9. Genotype Number Number of A1
A1A1 4 2X4
A1A2 41 41
A2A2 84
A1A3 25 25
A2A3 88
A3A3 32
Total 274
f(A1) = ((2 X 4) + 41 + 25) ÷ (2 X 274)
= (8 +41 + 25) ÷ 548
= 74 ÷ 548
= 0.135

10. Allelic frequencies at X linked locus
same principle
However remember for humans that males only have one X
So that
F(one allele = 2 X the homzygous genotype) + the number of
heterozygotes + the males with the phenotype all divided by the
number of alleles in the population (2 X females) plus males.

11. Hardy – Weinberg “law”
Frequencies of alleles and genotypes within a
population will remain in a particular balance or
equilibrium that is described by the equation
Consider a monohybrid cross, Aa X Aa
Frequency of A in population will be defined as p
Frequency of a in population will be defined as q

12. Gametes A (p) a (q)
A (p) AA(pp) Aa(pq)
a (q) Aa(pq) aa(qq)
Frequency of AA offspring is then p2
Frequency of aa offspring is then q2
Frequency of Aa offspring then 2pq
Frequency of an allele being present is = 1

13. p2 + 2pq + q2 = 1
Where p = frequency of “dominant” allele
and q = frequency of “recessive” allele
For the moth example
(0.9525)2 + (2 X (0.953 X 0.047)) + (0.047)2
0.907 + (2 x 0.045) + .002
.907 + .09 + .002 = .999
Is this good enough?

14. Can be extended to more than two alleles
Two alleles
(p + q)2 = 1
Three alleles
(p + q + r)2 = 1
And X – linked alleles
Can be used to det4ermine frequencies of one
allele if the presence of one allele is known

15. Conditions or assumptions for the Hardy –
Weinberg law to be true
Infinitely large population (?)
Randomly mating population (with respect to trait)
No mutation (with respect to locus or trait)
No migration (with respect to locus or trait)
No natural selection (with respect to locus or trait)
Frequencies of alleles do not change over time

17. Population variation
How is it quantitated?
Proportion of polymorphic loci
Heterozygosity

18. Population variation
Variation at many loci
How is it detected?
PCR
Sequencing
Protein electrophoresis
VNTRs
SNTRs
Synonymous vs. non-synonymous variations or
chnages

19. How is population variation of loci obtained
Random events
Mutation
Gain and loss of genes from the gene pool
Founder effect
Bottleneck effect
Random genetic drift
Selection
Migration

20. Mutations may be lost or fixed within a
population

22. Selection and speciation
Selection coefficient
Heterozygote superiority

23. Selection against recessive lethal

24. Fitness

26. Terms
Mendelian population
Gene pool
Genotypic frequencies
Hardy-Weinberg law
Genetic drift
Random mating
Cline
Random genetic drift