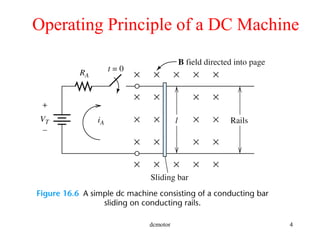
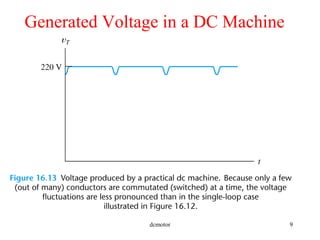
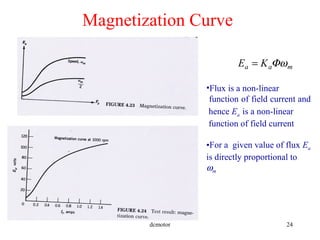
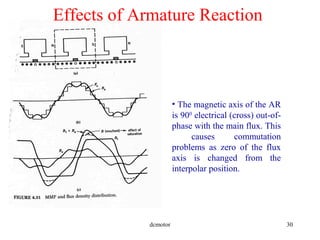
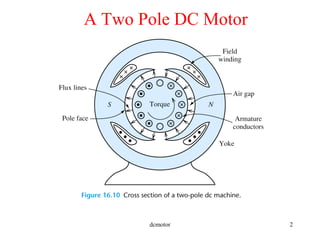
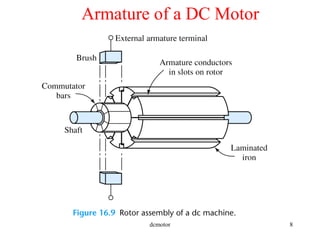
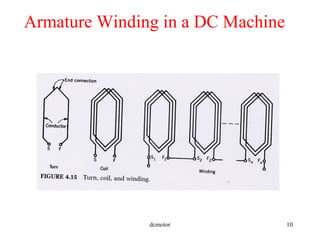
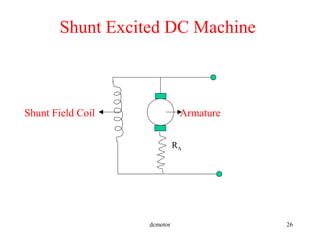
The document discusses the basics of DC motors and generators. It covers topics like: - The operating principles of DC machines and how they work as motors and generators. - Fleming's left and right hand rules for determining the direction of motion, induced voltage, and magnetic fields. - Components of DC machines like the armature, field coils, commutators, and different winding configurations. 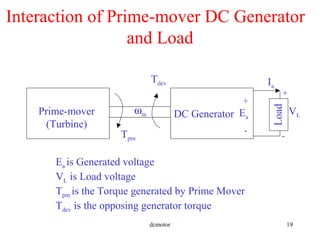- How torque, speed, input power, and output power are related in DC motors and generators. 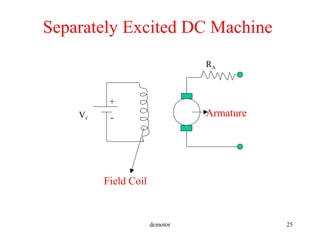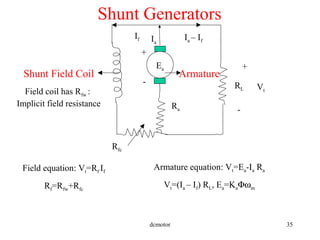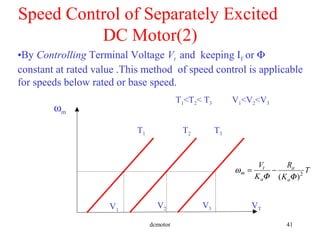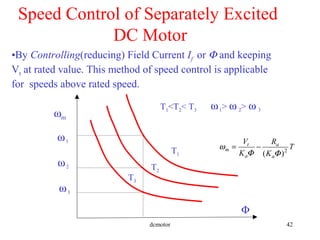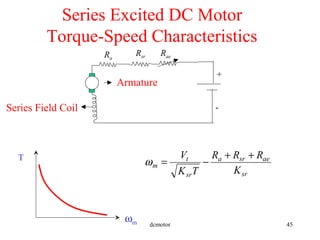- Characteristics and speed control methods for separately excited, series, and shunt DC machines. 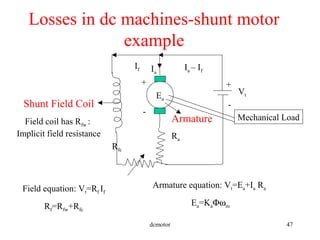- Losses that occur in DC machines and examples of calculations related to voltage, current, torque

1. dcmotor 1
Basics of a Electric Motor

2. dcmotor 2
A Two Pole DC Motor

3. dcmotor 3
A Four Pole DC Motor

4. dcmotor 4
Operating Principle of a DC Machine

5. dcmotor 5
FORE FINGER = MAGNETIC FIELD
900
900
900
MIDDLE FINGER= CURRENT
THUM
B
=
M
OTION
FORCE = B IAl
Fleming’s Left Hand Rule Or
Motor Rule

6. dcmotor 6
FORE FINGER = MAGNETIC FIELD
900
900
900
MIDDLE FINGER = INDUCED
VOLTAGE
TH
U
M
B
=
M
O
TIO
N
VOLTAGE = B l u
Fleming’s Right Hand Rule Or
Generator Rule

7. dcmotor 7
Action of a Commutator

8. dcmotor 8
Armature of a DC Motor

9. dcmotor 9
Generated Voltage in a DC Machine

10. dcmotor 10
Armature Winding in a DC Machine

11. dcmotor 11
Lap Winding of a DC Machine
• Used in high current
low voltage circuits
•Number of parallel paths
equals number of brushes
or poles

12. dcmotor 12
Wave Winding of a DC Machine
• Used in high voltage
low current circuits
•Number of parallel paths
always equals 2

13. dcmotor 13
Magnetic circuit of a 4 pole DC Machine

14. dcmotor 14
Magnetic circuit of a 2 pole DC Machine

15. dcmotor 15
Summary of a DC Machine
• Basically consists of
1. An electromagnetic or permanent magnetic structure called
field which is static
2. An Armature which rotates
• The Field produces a magnetic medium
• The Armature produces voltage and torque under the action
of the magnetic field

16. dcmotor 16
Deriving the induced voltage in a
DC Machine

17. dcmotor 17
Deriving the electromagnetic torque in a
DC Machine

18. dcmotor 18
Voltage and Torque developed in a
DC Machine
•Induced EMF, Ea = KaΦωm (volts)
•Developed Torque, Tdev = KaΦIa (Newton-meter
or Nm)
where ωm is the speed of the armature in rad/sec.,
Φ is the flux per pole in weber (Wb)
Ia is theArmature current
Ka is the machine constant

19. dcmotor 19
Interaction of Prime-mover DC Generator
and Load
Prime-mover
(Turbine)
DC Generator
Load
Ia
Tdev
ωm Ea
+
-
VL
+
-Tpm
Ea is Generated voltage
VL is Load voltage
Tpm is the Torque generated by Prime Mover
Tdev is the opposing generator torque

20. dcmotor 20
Interaction of the DC Motor
and Mechanical Load
DC Motor
Mechanical
Load
(Pump,
Compressor)
Tload
ωmEa
+
- Tdev
Ea is Back EMF
VT is Applied voltage
Tdev is the Torque developed by DC Motor
Tload is the opposing load torque
Ia
VT
+
--

21. dcmotor 21
Power Developed in a DC Machine
•Input mechanical power to dc generator
= Tdev ωm= KaΦIaωm =Ea Ia
= Output electric power to load
•Input electrical power to dc motor
= Ea Ia=KaΦ ωm Ia = Tdev ωm
= Output mechanical power to load
Neglecting Losses,

22. dcmotor 22
Equivalence of motor and generator
•In every generator there is a motor (Tdev opposes Tpm)
•In every motor there is a generator (Ea opposes VT)

23. dcmotor 23
Example of winding specific motor and
generator
Worked out on greenboard

24. dcmotor 24
Magnetization Curve
maa KE ωΦ=
•Flux is a non-linear
function of field current and
hence Ea is a non-linear
function of field current
•For a given value of flux Ea
is directly proportional to
ωm

25. dcmotor 25
Field Coil
Armature
RA
Vf
Separately Excited DC Machine
+
-

26. dcmotor 26
Shunt Field Coil Armature
RA
Shunt Excited DC Machine

27. dcmotor 27
Series Field Coil
Armature
RA
Series Excited DC Machine

28. dcmotor 28
Shunt Field Coil Armature
RA
Compound Excited DC Machine
Series Field Coil
•If the shunt and series field aid each other it is called a cumulatively
excited machine
•If the shunt and series field oppose each other it is called a differentially
excited machine

29. dcmotor 29
Armature Reaction(AR)
• AR is the magnetic field produced by the
armature current
•AR aids the main flux in one half of the
pole and opposes the main flux in the
other half of the pole
•However due to saturation of the pole
faces the net effect of AR is demagnetizing

30. dcmotor 30
Effects of Armature Reaction
• The magnetic axis of the AR
is 900
electrical (cross) out-of-
phase with the main flux. This
causes commutation
problems as zero of the flux
axis is changed from the
interpolar position.

31. dcmotor 31
Minimizing Armature Reaction
•Since AR reduces main flux, voltage in
generators and torque in motors reduces
with it. This is particularly objectionable
in steel rolling mills that require sudden
torque increase.
•Compensating windings put on pole
faces can effectively negate the effect
of AR. These windings are connected
in series with armature winding.

32. dcmotor 32
Minimizing commutation problems
•Smooth transfer of current during
commutation is hampered by
a) coil inductance and
b) voltage due to AR flux in the
interpolar axis. This voltage is called
reactance voltage.
•Can be minimized using interpoles.
They
produce an opposing field that cancels
out the AR in the interpolar region. Thus
this winding is also connected in series
with the armature winding.
Note: The UVic lab motors have
interpoles in them. This should be
connected in series with the armature
winding for experiments.

33. dcmotor 33
Question:
Can interpoles be
replaced by compensating
windings and vice-versa?
Why or why not?

34. dcmotor 34
Field Coil
Armature
Ra
Vf
Separately Excited DC Generator
+
-
Rf
Vt
+
-
Field equation: Vf=RfIf
If
Ia
+
-
Ea
Armature equation: Vt=Ea-IaRa
Vt=IaRL, Ea=KaΦωm
RL

35. dcmotor 35
Shunt Generators
Field equation: Vt=Rf If
Rf=Rfw+Rfc
Armature equation: Vt=Ea-Ia Ra
Vt=(Ia – If) RL, Ea=KaΦωm
Shunt Field Coil Armature
Ra
RL
If Ia
Ia – If
Vt
+
-
Rfc
Ea
+
-
Field coil has Rfw :
Implicit field resistance

36. dcmotor 36
Voltage build-up of shunt generators

37. dcmotor 37
Example on shunt generators’ buildup
For proper voltage build-up the
following are required:
• Residual magnetism
• Field MMF should aid residual
magnetism
•Field circuit resistance should be less
than critical
field circuit resistance

38. dcmotor 38
Field Coil
Armature
Ra
Vf
Separately Excited DC Motor
+
-
Rf
Vt
+
-
If
Ia
+
-
Ea
Armature equation: Ea=Vt-IaRa
Ea=KaΦωm
Field equation: Vf=RfIf

39. dcmotor 39
Field Coil
Armature
RA
Vf
Separately Excited DC Motor
Torque-speed Characteristics
+
-
ωm
T
T
K
R
K
V
a
a
a
t
m 2
)( ΦΦ
ω −=
Mechanical Load
+
-

40. dcmotor 40
Separately excited DC Motor-Example I
A dc motor has Ra =2 Ω, Ia=5 A, Ea = 220V, Nm = 1200 rpm.
Determine i) voltage applied to the armature, developed torque,
developed power . ii) Repeat with Nm = 1500 rpm. Assume same
Ia.
Solution on Greenboard

41. dcmotor 41
Speed Control of Separately Excited
DC Motor(2)
•By Controlling Terminal Voltage Vt and keeping If or Φ
constant at rated value .This method of speed control is applicable
for speeds below rated or base speed.
ωm
VT
T1 T2 T3
T1<T2< T3
T
K
R
K
V
a
a
a
t
m 2
)( ΦΦ
ω −=
V1<V2<V3
V1
V2 V3

42. dcmotor 42
Speed Control of Separately Excited
DC Motor
•By Controlling(reducing) Field Current If or Φ and keeping
Vt at rated value. This method of speed control is applicable
for speeds above rated speed.
ωm
T1
T2
T3
T1<T2< T3
Φ
T
K
R
K
V
a
a
a
t
m 2
)( ΦΦ
ω −=
ω1
ω1> ω 2> ω 3
ω2
ω3

43. dcmotor 43
Regions of operation of a Separately
Excited DC Motor

44. dcmotor 44
A separately excited dc motor with negligible armature resistance
operates at 1800 rpm under no-load with Vt =240V(rated voltage).
The rated speed of the motor is 1750 rpm.
i) Determine Vt if the motor has to operate at 1200 rpm under no-load.
ii) Determine Φ(flux/pole) if the motor has to operate at 2400 rpm
under no-load; given that K = 400/π.
iii) Determine the rated flux per pole of the machine.
Separately excited dc motor –Example 2
Solution on Greenboard

45. dcmotor 45
Series Field Coil
Armature
Ra
Series Excited DC Motor
Torque-Speed Characteristics
ωm
T
sr
aesra
sr
t
m
K
RRR
TK
V ++
−=ω
Rsr Rae
-
+

46. dcmotor 46
Losses in dc machines

47. dcmotor 47
Losses in dc machines-shunt motor
example
Field equation: Vt=Rf If
Rf=Rfw+Rfc
Armature equation: Vt=Ea+Ia Ra
Ea=KaΦωm
Shunt Field Coil
Armature
Ra
If Ia
Ia – If
Vt
+
-
Rfc
Ea
+
-
Field coil has Rfw :
Implicit field resistance
Mechanical Load