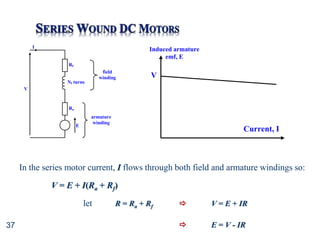
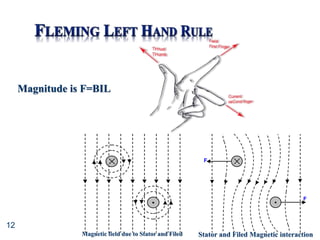
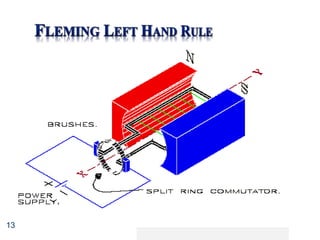
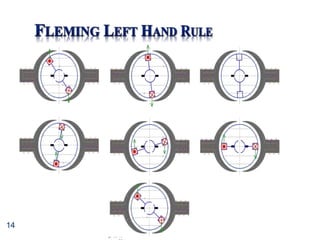
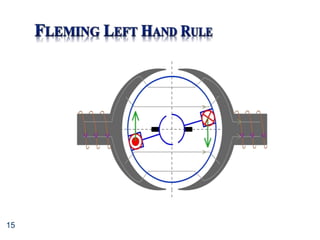
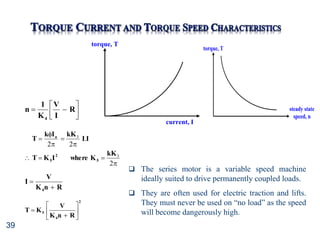
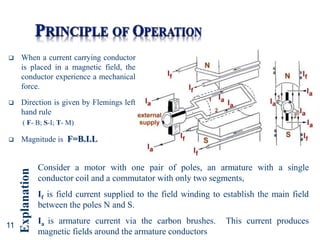
This document provides information about direct current (DC) motors, including: - The three main types of DC motors: shunt wound, series wound, and separately excited and their characteristics. - The principles of operation, construction, and torque-speed characteristics of DC motors. - How to calculate torque, speed, induced emf, and other parameters for DC motors. - Applications of the different DC motor types. 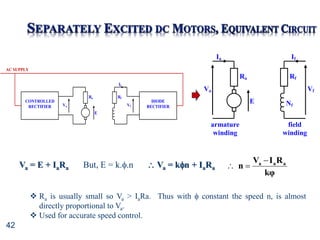- Circuit diagrams and equations for analyzing DC motor performance.

1. 1

2. 2
After completing this unit you:
 Will learn about the operation of direct current motors, different types of
DC motors and their applications
 Should be able to calculate
 Analyse the performance and principle of operation of DC motors.
 Calculate the torque speed characteristics for: -
 Shunt wound DC motors
 Series wound DC motors
 Separately excited DC motors

3. 3
 DC Motor Construction
 Principle of Operation
 Induced emf in the Armature
 Torque
 Armature Terminal Voltage
 Methods of Connection
 Shunt Wound DC Motor
 Series Wound DC Motor
 Separately Excited DC Motor

4. 4

5. 5

6. 6
Electric machines can be classified in terms of their energy
conversion characteristics.
Generators convert mechanical energy from a prime mover
(e.g., an internal combustion engine) to electrical form.
Examples of generators are those used in power-generating plants, or
automotive alternator.
Motors convert electrical energy to mechanical form.
Electric motors provide forces and torques to generate motion in countless
industrial applications.
For Example Machine tools, robots, punches, presses, mills, and propulsion
systems for electric vehicles are but a few examples of the application of electric
machines in engineering.

7. 7
Distinction can be made between different types of windings characterized by the nature of
the current they carry.
 If the current serves the purpose of providing a magnetic field and is independent of
the load, (it is called a magnetizing, or excitation, current) the winding is termed a
field winding.
(nearly always DC and are of relatively low power, since their only purpose is to
magnetize the core).
 However, if the winding carries only the load current, it is called an armature.
In DC and AC synchronous machines, separate windings exist to carry field and armature
currents.

8. 8
A Motor/Generator are made of
 Stator: This is the stationary part
 Rotor: This is the rotating part
Separated by an air gap

9. 9
 The rotor and stator each consist of
 Magnetic core,
 Electrical insulation, and
 Windings necessary to establish a magnetic flux (unless this is created by a permanent
magnet).
 The rotor is mounted on a bearing-supported shaft, which can be connected to:
 Mechanical loads (functioning as a motor), or
 A prime mover (functioning as a generator) by means of belts, pulleys, chains, or other
mechanical couplings.
 The windings carry electric currents that generate magnetic fields
(by virtue of Faraday’s law)

10. Brushes
Electrical
connector
between
armature and
power
Pressure is
adjusted using
the spring
Commutator
Mechanical
rectifier
converts ac to
dc
Made of copper
segment
insulated by
mica
Rotor:
Armature
conductor are
connected to the
Commutator
Stator
Produces an
external flux
+ + + =
DC Machine

11. 11
 When a current carrying conductor
is placed in a magnetic field, the
conductor experience a mechanical
force.
 Direction is given by Flemings left
hand rule
( F- B; S-I; T- M)
 Magnitude is F=B.I.L
Consider a motor with one pair of poles, an armature with a single
conductor coil and a commutator with only two segments,
If is field current supplied to the field winding to establish the main field
between the poles N and S.
Ia is armature current via the carbon brushes. This current produces
magnetic fields around the armature conductors
Explanation

12. 12
Magnitude is F=BIL
Magnetic field due to Stator and Filed
F
F
Stator and Filed Magnetic interaction

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18

19. 19

20. 20

21. 21

22. 22

23. 23

24. 24

25. 25

26.  As the coil rotates an emf is induced in each conductor which opposes the externally
supplied armature current, Ia.
 The external supply must overcome this emf if the machine is to continue motoring and
deliver mechanical power through its shaft.
 Faraday’s Law states that the
emf induced in a conductor = rate of change of flux linkages
 Taken over a period of time
Average emf induced in conductor = total flux linkage
total time of linkage
Therefore, if the coil rotating at n rev sec-1
Each conductor will be close to a particular pole 2n times per rotation
Each conductor will link with its magnetic flux for sec per rotation
26 





2n
1
So, When conductor 1 is close to N-pole:
Total flux emanating from that pole = 
Average emf induced in conductor1 = total flux linkage
total time of linkage
Volts
2nφ
2n
1
φ









27. 27
 Number of poles affects the induced emf
 Machines have several pairs of poles.
 For a machine with p pole pairs, the average emf in each conductor is given by:
 average emf induced = total flux per pole
in a conductor total time conductor is under a pole
Volts
2pnφ
2n
1
p
1
φ











Total emf induced = average emf induced  number of armatur
in armature winding in one conductor conductors in series
E = 2pn As
The number of poles (2p) and the number of armature conductors in series (As) are constant
for a particular machine. Therefore k = 2p As
E = kn Volts
Since the angular velocity,  = 2n Volts
φω
2π
k
E 

28. 28
Electrical power delivered = Armature emf  Armature current
to the armature
Pa = E  Ia
This power creates the torque to make the armature rotate.
Electrical torque developed = Electrical power delivered to the armature
in the armature Angular velocity
Remember: Power is the rate at which work is done; Work done in 1 s = force × distance
Power = work done / time taken
meters
Newton
I
φ
2π
k
ω
I
ω
φ
2π
k
ω
P
T a
a
a
e 









1
Mechanical torque|at the shaft = Electrical torque - “Lost” torque|due to frictional and other losses
The “lost” torque is small and will be ignored

29. 29
 The figure represents an equivalent circuit of an armature
 E is the induced emf
 Ra is the armature resistance
 The armature terminal voltage is given by:
Va = E + IaRa
E
Ra
Ia
Va

30. 30
The field and armature windings may be connected to:
 Independent supplies - separately excited
 Common supply - self excited
 Shunt wound: The field and armature windings are connected in
parallel
 Series wound: The field and armature windings are in series
 Compound wound: Has two field windings;
o One connected parallel with the armature and
o Other in series with the armature

31. 31
Field Winding:
S
N
I
S
iN
φ
f
f


Where, S is the reluctance,
N is the number of turns in the coil and
i is the coil current.
Armature Winding:
Armature terminal voltage, V = E + IaRa
V = kn + IaRa
with  constant, let K1 = k V = K1n + IaRa
1
a
a
K
R
I
V
n
speed
state
steady
The




V : External supply voltage
Rf :field winding resistance
are normally constant,
hence keeping If and
hence  constant.

32. 32
V/K1
speed, n
armature current, Ia
K
R
I
V
n
1
a
a


From Last Slide

33. 33
slide)
last
(from
K
R
I
V
n
1
a
a


2π
kφ
K
constant,
φ
With 2 
a
e I
φ
2π
k
T
Using 
torque, T
armature current, Ia
a
a
2 I
φ
2π
k
T
or
I
K
T 





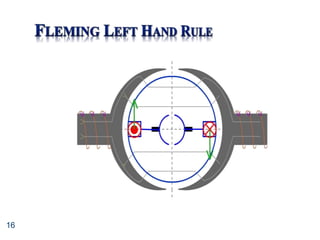
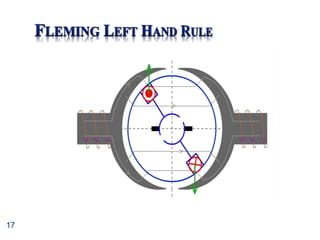
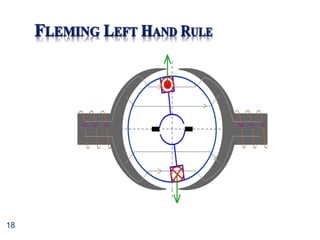
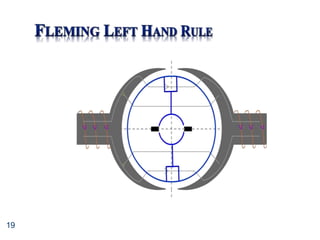
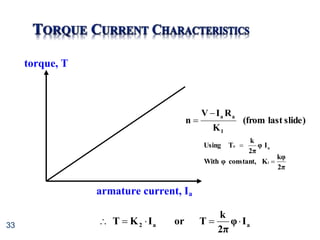
34. 34
K
R
I
V
n
1
a
a


n]
K
-
[V
R
K
T 1
a
2

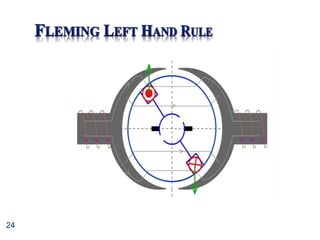
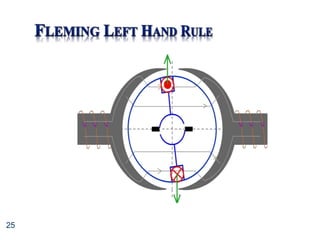
We had:
a
a
R
n
K
V
I 1


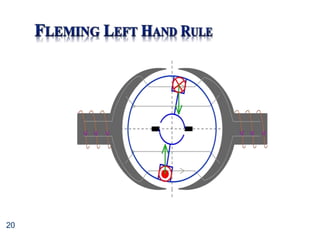
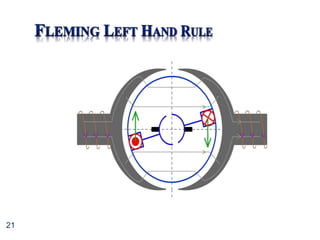
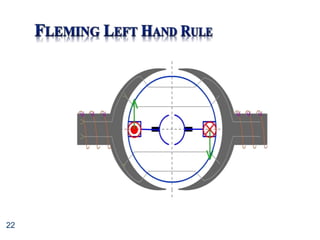
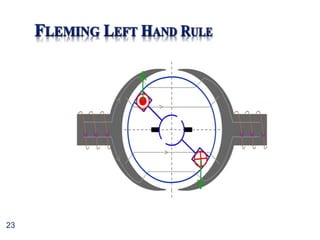
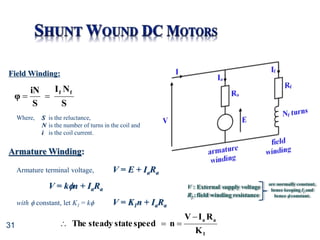
The torque-speed curve shows that shunt motors can be used to drive fairly constant
speed from no load to full torque
Therefore, ideal for use with machine tools, pumps, compressors etc.

35. 35
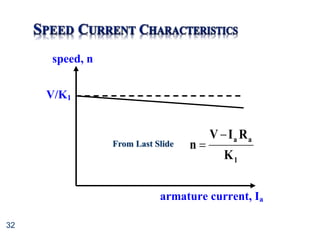
 A 220V dc shunt motor has an armature resistance of 0.8 and field winding
resistance of 220. The motor field characteristic [k versus field current] is
shown in Figure
a) Calculate the field current
If the motor drives a constant load torque of 17.5Nm, calculate
b) armature current
c) speed
Field current
(A)
0.5 1.5
0.0 1.0
2
4
6
k (Vs/rev)

36. 36
5
.
5
16
220 

n
Speed = 37.1 rev sec-1
= 2225 rev min-1.

37. 37
In the series motor current, I flows through both field and armature windings so:
V = E + I(Ra + Rf)
let R = Ra + Rf  V = E + IR
 E = V - IR
E
Ra
V
I
Nf turns
Rf
armature
winding
field
winding V
Induced armature
emf, E
Current, I

38. 38








 R
I
V
K
n
4
1
All dc motors, flux,   field winding current
For Series wound motor   I;  = K3I
N.B. this assumption only applies for low currents.
E = kn
E = kK3In
E = K4In where K4 = kK3
 V = K4.I.n + I.R
steady state
speed, n
current, I
E
Ra
V
I
Nf turns
Rf
armature
winding
field
winding

39. 39
torque, T
current, I
torque, T
steady state
speed, n







 R
I
V
K
1
n
4









2
.
2
2
3
3
kK
K
where
I
K
T
I
I
kK
I
k
T
5
2
5
a
R
n
K
V
I
4 

2
4
5
R
n
K
V
K
T 







 The series motor is a variable speed machine
ideally suited to drive permanently coupled loads.
 They are often used for electric traction and lifts.
They must never be used on “no load” as the speed
will become dangerously high.

40. 40
A 220V dc series motor has armature and field resistances of 0.2 and 0.5
respectively. When running at 1000 rev min-1 the motor draws 10A from the
supply. Calculate the torque delivered.

41. 41
CONTROLLED
RECTIFIER
E
Ra
Va
Rf
If
DIODE
RECTIFIER
Vf
AC SUPPLY
For accurate speed control it is advisable to use a separately excited motor
i.e. Armature and Field Windings supplied through independent dc
rectifiers
 The diode rectifier supplies constant field current maintaining a fixed value of flux, .
 The controlled rectifier (supplying the armature winding) provides a fully variable
armature terminal voltage, Va.

42. 42
E
Ra
Va
Rf
If
Vf
Ia
Nf
armature
winding
field
winding
Va = E + IaRa But, E = k..n  Va = kn + IaRa
kφ
R
I
V
n a
a
a 


CONTROLLED
RECTIFIER
E
Ra
Va
Rf
If
DIODE
RECTIFIER
Vf
AC SUPPLY
 Ra is usually small so Va > IaRa. Thus with  constant the speed n, is almost
directly proportional to Va.
 Used for accurate speed control.

43. 43
Today we learnt about
 DC motors
 The three types of DC motors
 Shunt wound DC motors
 Series wound DC motors
 Separately excited DC motor
 and their applications
 We also touched on how to:
 Analyse the performance and principle of operation of DC motors.
 Calculate the torque speed characteristics for the three
different types

44. 44
Q1 A 240V dc shunt motor has armature and field resistances 0.2  and 320  respectively. The motor
drives a load at a speed of 950 rev min-1 and the armature current is 50A. Assuming that the flux is
directly proportional to the field current, calculate the additional resistance necessary in the field
circuit to increase the speed to 1100 rev min-1 while maintaining the armature current constant.
Calculate the speed of the machine with the original field current and an armature current of 90A.
50.5 , 917 rev min-1
Q2 A 230V dc shunt motor has armature and field resistances of 0.3  and 140  respectively. Calculate
the induced emf and the torque developed by the motor when it runs at a speed of 800 rev min-1 and
the armature current is 2A.
To drive a larger load at 1000 rev min-1 an additional resistance, R is connected in series with the
field winding. In this situation the armature current is 30A. Calculate the new induced emf and
torque and the value of R. Assume that the flux is directly proportional to the field current.
229.4V, 5.48Nm; 221V, 63.3Nm, 41.7 
Q3 A 240V dc series motor has armature and field resistances of 0.5  and 1  respectively. When
running at 1200 rev min-1 the motor draws 15A from the supply. Calculate the torque delivered.
A 2  resistor is connected in series with the motor. The torque is adjusted so that the armature
current remains unchanged. Calculate the new speed and torque. 26Nm; 1034 rev min-1;
26Nm
Q4 A 550V dc series motor with an armature resistance of 0.35  and and field resistance of 0.15 
drives a load at a speed of 750 rev min-1. The supply current is 74A. Calculate the load torque.
The load torque is doubled and the supply current rises to 110A. Calculate the new speed and power
output. 483.3Nm; 537.8 rev min-1; 54.45 kW