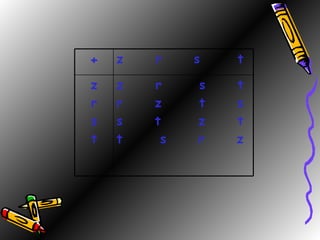
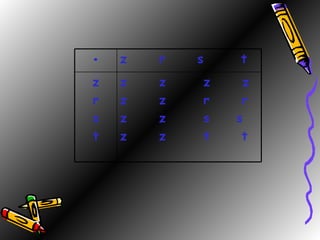
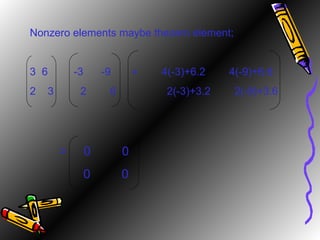
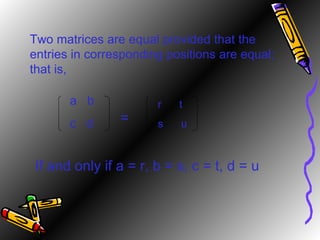The document defines a ring as a set equipped with two binary operations, addition and multiplication, that satisfy certain properties like closure, associativity, identity elements, and distributivity. It provides examples of rings like the integers Z, even integers, and a set of four elements with a specified addition and multiplication tables. The document also discusses the ring of 2x2 matrices over the real numbers with matrix addition and multiplication defined entry-wise.

1. Definition of Rings and Examples By: John Wilson Calalo and Daryl Sacay

2. A ring is a none empty set R equipped with two operations that satisfy the following axioms. For all a, b, c, є R:

3. 1. If a є R and b є R, then a+b є R [closure for addition] 2. a + (b + c) = (a + b) + c [associative addition] 3. a + b = b + a [commutative addition] 4. There is an element O R in R such that a + O R = a O R + a for every a є R [additive identity or zero element]

4. 5. For each a є R, the equation a + x = O R has a solution in R. 6. If a є R and b є R, then ab є R. [closure for multiplication] 7. A (bc) = (ab) c [associative multiplication] 8. A (b + c) = ab + ac and (a + b) c = ac + bc [distributive laws]

5. Commutative Ring is a ring R that satisfies this axiom: • ab = ba for all a, b [commutative multiplication]

6. Example: The set of integers Z, with the usual addition and multiplication, is a commutative ring with identity.

7. Let E be the set of even integers with the usual addition and multiplication

8. The set of odd integers with the usual addition and multiplication is not a ring.

9. The set T= {r, s, t, z} equipped w/ the addition and multiplication defined by the following tables is a ring.

10. z r s t r z t s s t z t t s r z z r s t z r s t +

11. z z z z z z r r z z s s z z t t z r s t z r s t •

12. Let  (R) be the set of all 2x2 matrices over the real numbers, that is,  (R) consist of all arrays a b c d

13. Two matrices are equal provided that the entries in corresponding positions are equal; that is, a b c d = r t s u If and only if a = r, b = s, c = t, d = u

14. For example, 4 0 2+2 0 but 1 3 ≠ 3 5 -3 1 1-4 1 5 2 1 2

15. Multiplication of Matrices is defined by: a b c d = w x y z aw=by ax=bz cw=dy cx=dz

16. For example, 3 1 -5 2.1+3.6 2(-5) +3.7 0 -4 6 7 0.1=(-4)6 0(-5)+(-4)(7)

17. The multiplicative identity element is the matrix I = 1 0 0 1

18. For instance a b 1 0 = a.1+b.0 a.0+b.1 c d 0 1 c.1+d.0 c.0+d.1 = a b c d

19. Nonzero elements maybe thezero element; 6 -3 -9 = 4(-3)+6.2 4(-9)+6.6 2 3 2 6 2(-3)+3.2 2(-9)+3.6 = 0 0 0 0