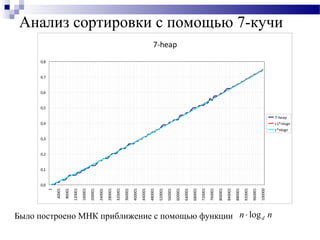
Документ охватывает тему d-куч, включая их структуру, основные операции и применения. Описаны основные характеристики d-куч, такие как хранение, алгоритмы вставки, удаления и уменьшения ключа, а также результаты экспериментов. Также приведены примеры реализации операций с d-кучами, включая сложности выполнения различных задач.









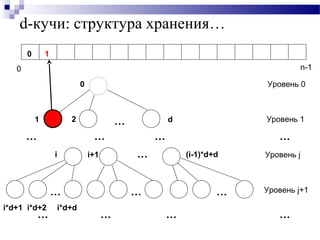


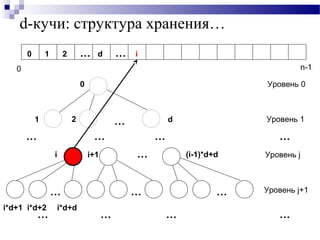

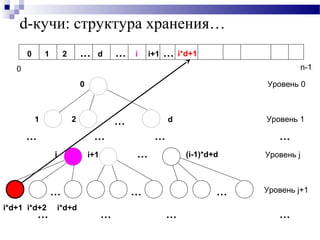
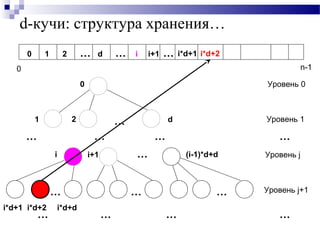
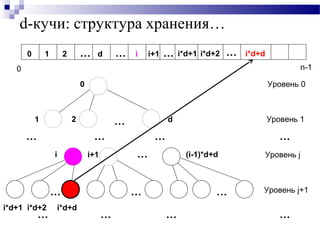
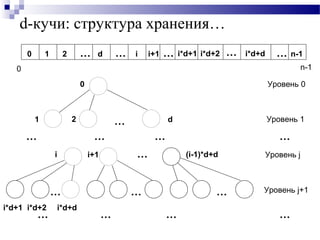
![d-кучи: структура хранения…
Пример: n = 8, d = 3
key[n] = [2, 2, 4, 5, 5, 6, 6, 5]
2
2 4 5
5 6 6 5
0
1
5
2
4
3
76](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-19-320.jpg)



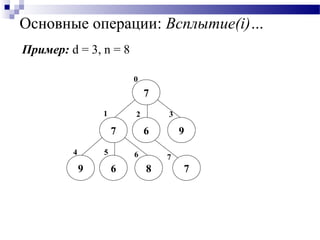
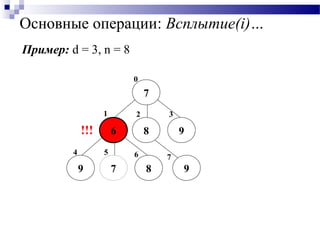
![Основные операции: Всплытие(i)…
Всплытие(i)
Применяется для элемента x в узле i , нарушающего
кучеобразный порядок, т.е если ключ элемента меньше
ключа родителя.
Procedure Всплытие(i)
begin
p := (i-1)div d
while (i≠0) and (key[p]>key[i]) do
begin
tr(i,p);
i:= p; p:=(i-1)div d
end;
end;
Вычислительная сложность: )(log nO d](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-23-320.jpg)





![Основные операции: Погружение(i)…
Погружение(i)
Применяется для элемента x в узле i , нарушающего
кучеобразный порядок, т.е если ключ элемента больше
ключа потомка.
Вспомогательная функция min_child(i):
Function min_child(i)
begin
if (i*d+1>=n) return 0;
else
begin
s:=i*d+1; min_key:=key[s]; last:=(i+1)*d;
if (last>=n) last:=n-1;
for j:=s+1 to j:=last do
begin
if (min_key > key[j]) min_key=key[j]; s=j;
return s;
end;
end;](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-31-320.jpg)
![Основные операции: Погружение(i)…
Procedure Погружение(i)
begin
s:=min_child(i);
while (s≠0) and (key[i]>key[s])
begin
tr(i,s);
i:=s;
s:=min_child(i);
end;
end;
Вычислительная сложность: )log( ndO d⋅](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-32-320.jpg)







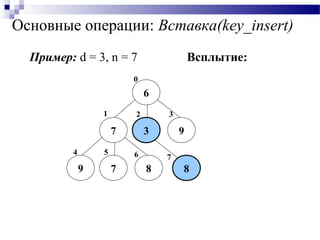
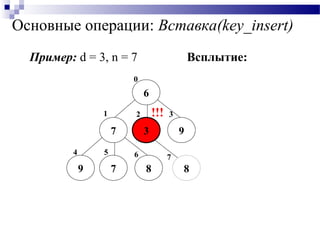
![Основные операции: Вставка(key_insert)
Вставка(key_insert):
Добавление n+1 узла с номером n;
Применение операции Всплытие(n).
Procedure Вставка(key_insert)
begin
key[n]:=key_insert;
ВСПЛЫТИЕ(n);
n:=n+1;
end;
Вычислительная сложность: )(log nO d](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-40-320.jpg)







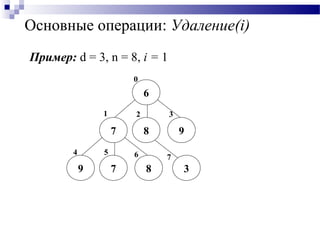
![Основные операции: Удаление(i)
Удаление(i):
Перенести последний элемент на место удаляемого
элемента с номером i;
Если узел i имеет родителя с большим ключом, то
применяется операции Всплытие(i), иначе операция
Погружение(i)
Procedure Удаление(i)
begin
key[i]:=key[n-1]; n:=n-1;
if (i≠0) and (key[i]<key[(i-1)div d] then ВСПЛЫТИЕ(i)
else ПОГРУЖЕНИЕ(i);
end;
Вычислительная сложность: )log( ndO d⋅](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-50-320.jpg)






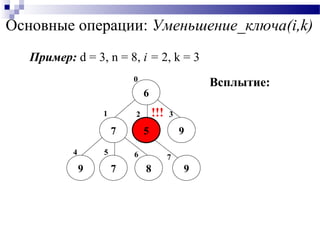
![Основные операции: Уменьшение_ключа(i,k)
Уменьшение_ключа(i,k):
Уменьшить ключ элемента в узле i на заданную
константу
k = const ;
Выполнить операцию Всплытие(i).
Procedure Уменьшение_ключа(i,k)
begin
key[i]:=key[i]-k;
ВСПЛЫТИЕ(i);
end;
Вычислительная сложность: )(log nO d](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-58-320.jpg)






![Сортировка массива…
Задача сортировки с использованием d-куч:
Требуется упорядочить массив key[n] по неубыванию,
путем перестановки его элементов с использованием d-
кучи.
На выходе требуется получить последовательность
key[1] ≤key[2] ≤… ≤key[n].](https://image.slidesharecdn.com/d-eoeeeoieiaiaieafinal-151129152443-lva1-app6892/85/D-66-320.jpg)