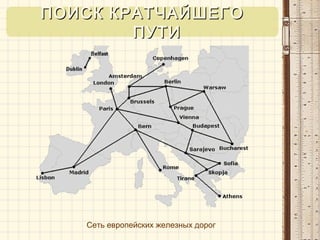
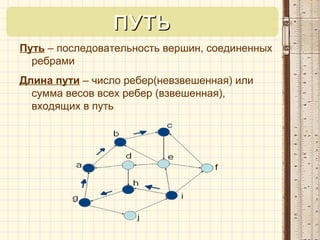
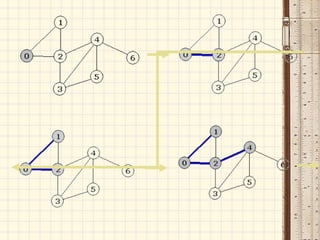
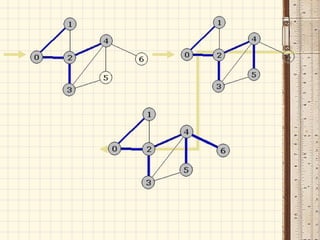
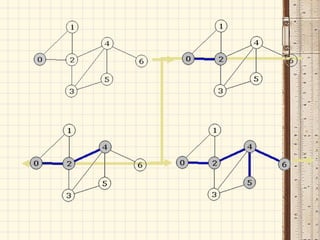
Документ описывает основные понятия и структуры данных, используемые в C++ для работы с графами и библиотекой STL. Он охватывает различные контейнеры, такие как векторы, множества и карты, а также методы для представления графов, такие как матрицы смежности и списки смежностей. Также приводятся алгоритмы, связанные с графами, включая поиск в ширину и поиск в глубину.




![VECTOR – динамический массив
– size() – возвращает текущий размер вектора
– begin() – ,возвращает итератор установленный на начало вектора
– end() - ,возвращает итератор установленный на конец вектора
– push_back() – записывает значение в конец вектора
– insert() – ,записывает значение непосредственно перед элементом
на который ссылается итератор
– erase() – удаляет элемент из вектора
– …
vector<char> iv; //пустой вектор
int i; //счетчик
for (i=0; i<10; i++) v[i] = i + ’a’; //заполнение
//устанавливаем итератор в конец
vector<char>::iterator p=v.end();
v.insert (p,3,’X’); //вставляем три символа Х в
вектор
//выводим на экран содержимое вектора
for (i=0; i<v.size(); i++) cout<< v[i] << “ “;
КОНТЕЙНЕРЫКОНТЕЙНЕРЫ](https://image.slidesharecdn.com/6-190626110323/85/6-0a-5-320.jpg)

![SET – ;упорядоченные уникальные значения
MAP – а :ссоциативный контейнер
уникальный ключ – значение
map<string, string> m1; //ключ и значение – строковый тип
//заполнение: ключ-значение хранится с помощью стандартного типа пары
m1.insert(pair<string, string>("apple", "a small red fruit"));
m1.insert(pair<string, string>("orange", "a small orange fruit"));
m1["banana"] = "a long yellow fruit"; //заполнение
//вывод на экран вариант 1
map<string, string>::iterator it = m1.begin();
for ( ; it != m1.end(); it++) {
cout << it->first << ": " << it->second << endl;
}
//вывод на экран вариант 2
cout << m1["apple"] << endl;
cout << m1["orange"] << endl;
cout << m1["banana"] << endl;
КОНТЕЙНЕРЫКОНТЕЙНЕРЫ](https://image.slidesharecdn.com/6-190626110323/85/6-0a-7-320.jpg)