This document contains a 10 question multiple choice test covering topics in mathematics, physics, chemistry, and general knowledge. 1) The first question involves finding the total length of fencing for a garden with angles in an arithmetic progression. 2) The second question deals with identifying properties of angles and lengths in a right triangle diagram. 3) The third question concerns calculating ratios of lengths in a semicircle diagram. The test continues with additional multiple choice questions testing a variety of concepts.

1. ,AH
~
1fl'l1i;f;
1636
2012 (£)
,'iN:!$ sfl-1 ,.,...
.,.,.
qf1tm !4QIFJ
[±]~rrR rm
; 3;00 ri? 'J.V1fw ' 200 3/'i/;
I. .,-;ot ~'>/} iO/ '1/fZPf 'J.fr t I PI <riR!i "J#a'61 0 ...... f'l 4ffl (20 'fl'1 'A' • + 40 >11'1
'B' + 60 >m 'C' It 1 •sn ~ ""' (MCQ)mo 'If/ f 1 "'"""' "'~ 'A' if w
- ~~ .,,. ""''R' ~ 2s •..,r""''«'I'C iT" 20 mo'J""" .r.t ~ , .rt
f.iflf#rr '1 ~ tJ?'J'i It tJm"( rtf: Til;! ffi1 .P<i<'i tm-7 '7f1f'A' W I S.~ 'B' ?1' 25 7f'liT
tff11 'C' it20 m7W Gift OTh1 lift vm.ofl 1
2. JF.T" fi .Jffof1! 't fWt iff1T t I Jl!rn ~ ~ J(R rlto< W fT{¥ /8ri W~ ~ VTht
~ fil; yfl<rw *'fiS '1;1 Jli< w,l) it <rrn 0tf il fl't-'lft <riJ f. 1 'fR #I t m"""
~~m w1f1mm ....m ., ~ <K< <~>'~~ t 1 <711 rm w"""' "" llli >fl ,;.,
R I >'f ~ >f ••1 ...,. - <li f<lrr ~ R ..,.... f. I
3. ~ ft:l ;j ?"ES 1 4 /tf w ~ :rr .JtrRT m. lN't ~ JtVof1 GID ~7 rtf vt.err
!Jfi'd~J iOI 11"'i>t Crf6'l I JiMt ll7i'lJ!R >it il!'l<li t I
4. ..,. .w>t~ .w.~ """,_if""m ~ ~ ~ • Jb? ~ ..r.r"
'fMW ~ ,wf 'fit ~ W<fl "" >f I "" 'l'f/ '1/!1 <ifllmlf "' - 3 t fit; <Ia'
""" ~ .r ~ •f f#nf Oil ~ - w"""" fit ~ " - .. ~
~ "" <Ttl ~ wJt~d 'llff .,.. 'l1fffl fi)fmt rsimt: ...mt d-1. fi)fmt i1liWfl
;my, !Jf/<fifir "' ~ '" rnfilff. ('1 Wlflfl ~ I
). ~'A' r'f rrt:i!t# rt'R 2 W , lfPT'B' ~ ~ Vf'J rt 3 #tf iM tlftt 'C t'l ~ rTR
4.75 tJhr. iliT 8 I ll~'iR l1ffif am7 iliT iittiJI?I<(; 1J!llhlr.r "'1111 'A' il@ O.S Jiq; rrur
,wr'B' t)@ 0.75 #111 'lt fitrr11 Vf1llT11 I "'f1TT 'C' ¥}; iflffW fG fttv lltUJK))M ~7ft'~'
#I
6. ?-,7tf 'A' m'H 'loJ1'I1 'U' Jt J1F.T.1; VR <$ 4tQ t:R R-(flt4 n{' mt I 1 ffl Wm,p, 'W
f?P1;<q {/ ~ M/111 7,.,r<'/' # I "-'TWft """"' llT'f "'1 «t/ :nom """""' ~
¥'> t I '11'1 'C ~ •'filoli J1R Oi1 ''!1'5" 'll " '!<1' W.,{W/' ~- ~ ;:1 .,..; f I
'iF1 'C' ~ ..,;, v.- lit fl>ll - o;; a# im'J - W tl IM:;c !1R1 ~ I W#
f1!ll fiR;;qf "" _, orfl ""' W ¢ - - 'ftJ fttJJ "'1"11 I
7. ~ ilrnl......R.-"'-~ lf{Fiil q;r JPh1f <Snt fi..!.!S' mo) .t ~ fi sn .Jh
JA1 ;'11!1 <rWu/1 rtJ1r;'.,.W., grn<J "' W1$IJf t I
8. ~ 05) ~ ~ "" q'"if W~ fbtf >/~? '511 >JI 'ltfHftrn mftt/ I
9. ·rR>fT ,..,,Et..,.; .. 'fil<fl 'jft<m '>'f7 ~ '1> ~ ~~.:7 05) ...... #q <fl{i);vI
l0. ill&if:d<> q;r OWPr Ill?') .:J ~I'J'f/l1 'ltf t I
(i);lfl llY'f •Y lii?Mil Ill •NJ i/ J/rvf/ """""'!1'1d #'II I
""...........................
.-if;m 'Ill '1'/ormtiT8 "' if ~
ll<ill1 ( I
..............................
S/07 RD11Z-4AI+-1A

2. S/07R0/12-V.H-1B

3. ( '1171 A )
I. (><-J2) 2. (n -2)
3.
(·:-~) 4. (H2)
2. ~ ~ ~"'iifm &i<ljftt d; 'iTf'/l <t Jim Y71lfrr1
W;fi >f f. Jilv m<l u'n!l :fi11 10-00 41<? # 1
iff'( <til ,. .r; ilj1'T ~ 41<? 'i ;j
I. 60.00
3. 12.68
2. 47.32
4. 22.68
3. im1 'r <mfil "''Ff' ti1mt "'fvm 1P1 u;m AB
tJ rrfif AQ = 2AP rh f.rr.r if W~ ~
WI 3?
~A •
I. LAPB=~LAQB
2. LAPB~2LAQB
3. LAPB= LA(}B
4. LAPB=!._LAQB
4
3
( PART;J
I. (;;-J2) 2. (:r-2)
3. (;-~) 4. (H2)
2. 'l'hc <m,gks of a right·angiOO triangle shaped g;~.rdcn
arc in arithmclic progrc.ssion nnd the smalkst side is
10.00 m. llll~ total length of 1hc fencing of the
f,Wdcn in m i$
I. 60.00
3. 12.68
2. 47.32
4. 22.6$
3. AD is the diameter of the scmicir'Cic: ~s shown itt the
diagram. IfAQ =2Al' then which oflhe following
is comet?
• •
I. L APli=~LAQll
2. L APB =2LAQ8
). LAPB= LAQB
4. LAPB =!._LAQB .
4
4. rmtmf $ '{Ui ~A i1ft W<ui&Jt 25% rrflrtTd 4.
"'? •~ 1l "'flf) t ""'lilt WV B<til ~ ~ SO%
kliri# t I oR "1.1' A >!lr D .,;} q;/'IT'f
,;:;td&n~ WTTR '# ffl ~ iTfi ;mnq 1711.!! B $/k
W~t< A ;j; ~ <it fflFii 'liT &JWiiitTf1 :
The robbil popula1ion in cooJ.munJiy Ai.ncr<.'3.'~l> 3t
25% per year while that in B increases at 50% per
ycat. If the present J)OJ)ulstion.~ of A and Barc
tqt.•a1,1hera1io of1he m1mbc1'ofthe rabbits in a ·to
that in Aafter 2 )·e<•ri> will be
I. 1.44
3. 1.90
. 2. 1.72
4. 1.25
I. 1.44
3. 1.90
2. 1.72
4. 1.25
•
'

4. ,...
!-. 0.: ., H1 v~ 4f: 4 W& #5lJ ~ Jir.1ff't :ml s.
e ,..,-;t *lSOOI'i st11 <*Jd.$Rtll <K ct( t: 4
r.tot~ rm vw &'"1 :;.-<i if rG:r. a? n P JT#l
,;-1rd tr >i1 fRi Rr H•~ ?W w~,.... ~' ;;rrtftf
+ " ,f ,.
~·1<1 fl.-,·~ "fo? $ P!.J.''(;J' ;n rft'qlfN I50°ff rrr
Nmr fm1 ~ m'5r?..•,r m ' ~J!tff.'~('f If~ Cif/(11 (!II r~11( G.'f;{ ;p, Si.-.'uN i;'r•tl cll/td
1'?
.,.. $J'./~
·' Jl',l2 .). 211,,
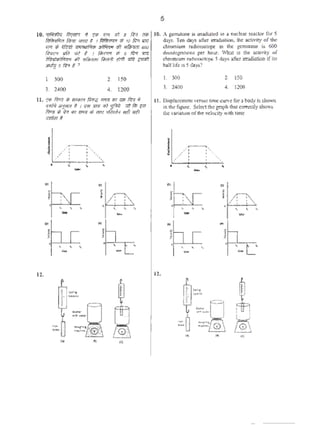
6. trfkP <! ..'-!J-:f:i ~?. ~ $lP1 wif *~..t:
m-'IN «R" t 1 sa ~:::..J Jt/..;-:r,r;-p trr ~
6
'
.,.. ot ~ ~ . il .., "" "" ~ "" ~
.st8 m;:~;o~ ~ ft!«ri mzR i -~ $ f:ft:pp(
'"'"I:J'i'l OH1 J::i ·JY"fl;-;i,'<" n FP:1
1. fit11:.1! ~::r.r.!J ~ iJ ~rr11 en fmt ar.rr:r
2. f*Fl ;v;;r-7 ~ j.;.j f.rrl'fl PI '171ft 1JP;
J. /1}w:t ;,;~r-~ tJ} j.ci f.;rrRT tl1 ~ vrrTI¥
4. flfsM t1i 3Jf4q !o71ff!;jJ.'f ;.R #r! Q} ~Tfilf
4
r-,.u ~~ t3eh of0; and H1 Ill: in N-'0 St"p2t8tt
C()tl(3:inctS, c.xh of OlUnv V0 3r.d at lSO <-c300 I
acmosphen 'The Cn Jrt" nl3de to ua.::;. 1n a lhm:!
c<>•':alf'l~r to rorm water vapQUr unlil H! ts
exhausted. 'he-n the tcmpc:r..uuce of the mixturt in
1he lhirtl cont:unt<r w:t.s n:~lored to 150 "C, ltl;
prtssurt became l Olmo~ph~::rc:. 'llle votum~ of th>!
1]1ird comnincr mUlll b'l)
L v. 2. 5Vc/4
3. 3V0r2 4. 2Y,-.
Hclium mel :lJt06 PSf5 in '"'0 ~ (:(l;'lUinm
.ue at the $:!me ~~~~~ and so tuve diff~r~11
root-mc-m-sqtaart (r.m.s.) ~·c&oaliCS. 'The t'0 3tC'
rni'~ iu ._ thud C'OfiQU'KI' keepirlg dlc S3mr
temp:n1urc. 'Ol:- r.rrt.) ~·clOCIC)' ofthe helium atoms
ut th-e mi:uurei$
1. mf>rc 1h3.ll what h w:.ll before mixing.
2. l<:s..~ than what it WtS before mixins.
3. .equ~l to wh:u h was before mixing.
4. t-quul 10 lh:.u ofat&On lltoms in the mixtutc:,
7. WiJ'1 ',J} iJ.t(;N';'r if tmfl·,ifi ~ il't1 IJ'qflt'f
R1m CfmT # ;;rf;ftJ; ~ 7. lllc mincrJI talc is used'" the manufacture ofsoap
because it
(0) J1<iR "" """"" .,.,; t
{b)~ ...,j~~
(C) 'JW ti!7 ~
(d) :pm~ t .Jh? r•/IH :R ~ ~ I
:r-rj"'' ~ I) u#r/11/;r,m'!"""' ..-1) ~/.~ >
I. (d)
3. (•) "" (b)
2. (!!) Jllol (o)
4. (n) """(d)
(a} grvcsbull;10lllO pn>du<l
(b) killsbo<lello
(c) gn-.s fr.lgr>n..
(d) is sot 3nd does not scr.uch l.hc $kin
Which ofthe atxwcsr.uen1cnts Isfan; <::orre<::t?
I. (d)
3. .(a) and(b)
2. (a) Md (c)
4. (n) and (d)
R. 100 Wf -Jit.'iri0til <l!fint; X·51h0 i.W ~~· ~ 8.
lllr<tfflt-f J'rJf~ g. ~ ~ li lSO"W. li'f !10
PM~ U<Ji (i$1 ~r.n I # qwf ;t Q'tilln' J.~
~00 &ofan inor&nnic compound X·SH~ wntainint;:
o. 'O):nite mtpu.rity wa~ k.epl m "n ,we-nat ISG "Cfor
60 minut-es. Th: wcaghl ort.hc residue after h<:3tirtg
is Sg. The petenJt3ee ofunpunly in X wasITi1 ¥>f s WI ~~ I 1 x ~ Jt§f; ri s;fllw
<1:
I. 10
3. 20
2. 8
4. 80
9. '!11f RTi• v;f!) >r ?f"'""'" iii! t'>' :Jo1!-tll: '·71
ow ljf;ll wf!: q/t w
I. ~·~ 101/ilvJ <{{ em
2. 7;41 IS!ir.r iill45° ..;Jofro ~~"' ~)qr
3. J,TI./iltl ;I; i~Nb'Z') rn ll:11f
4 wtnt ~w t/l rim"
1. iO
3. 2()
2. 8
•. so
9. On a tercain t'lighcthe mnnn ln 1t.s wa.,ing ph3Se w.lS
s h3Jf-moon. At midniQI111hc moon will be
1. on llleeas(em hori1.on.
2. at456
angubr J:ei&h1 ~bove the eastern hori:ron.
3. at the 7.enilh.
4. on the we!tcm horir.on.

5. 10. ~ ~ , ~ ..... "" s f?'l 11'0
~-t/i,u ~ f1I'R'IT # I Jtl%rt=J., ~ tO ~ ~
r<'l f/1 llhl ~ ~ oil ~ 601)
~ l1fi} ~ t I ~ ;f; S ft.r m:
~~•• oil ..a.- Rio'~/ tMt 1Ift ~
3Mgsfrlt'
1.300
3. 2400
2. ISO
4. 1200
11. (/'iff 1'1«$ 1/1 """""' #?;;: """ <;;; .,.. fW #
<flfil >f:JIII~ t I ~W '1/W "'' 'J{itil oil fit ;w
filvs W~" tm wr11 lh.. ~' qf?<rf:r Htf. wt.J
mmt
!
•
' .
~ .' o .' •... ' ' '• '
..,. .• ..• ' ... ' '
.. ..
f f
'
• ' ' '•....
.. ..
g
• '• '••
' '... ""'
11.
t_
r.... r-=- ~
~-u
- =10
,_.
- , 0
"'
,. 10
JO. A £!:m~Wil1o ill itradLatcd in ~ nuclear reacror for 5
days. Ten da)'l after irradl.llion, lhc :activity of the
(hromi~o~m r1dioisorope ll1 the scmston: is 600
dWn.ICVJhOns per ho~.a. Wb:n is tbe aetivity of
ehronuum NCIIICM$0topc 5 days 11er irr3d.iatioo ifUs
halfhfc ISS <lays?
l.lOO
l. 2400
2. ISO
4. 1200
J1. Displacement ...mus limeeurve fot a body is shown
in the f'igul'(. Scloct tho groph fl'mt corrt."C.tly shows
the v3ritliCin ofdH: vdocily with litne
''
! ••' ' ' .·' ' ' ·.• .. ' ..•• ' '.
' ._ ' •
.. ..•
I
•J
'
• •• ' • '-.. ..k
J} '
• '•••
' '
·-
l l.
~
.....~ ....
--...
.. .. ..

6. I~'IJ A <A ;stfi.fr;:r;r lff!i 0.5 fi'!;.:;T. q:ufi ~ ifi!i! ,9;?,·
~ . -o ~· .•• .W I ~ fJN! ), W•:;if, ~/1 • f W{P.,'4'f1 ~
,}«"<!'~"'' ~ uvz rir:: (' :t ~ ~ t:tFft >i ~f?.tf'l
:.v..r. ft"iW w·~? t .•<F.TlPf.wr ~ ,j,~ 0.4 fit.rn.
;:r,m; t. 1 .~ '11 rtflter? ffi1l <:7ifi:1f!
I. ;~.o ,,)en 2. 2.9 .L?t;m
3. 3.i .;m.lil 4. ~.$ ~1)'!
u. fZ'i,~ i1i ;:).!}' t¥ ~~ qt.' :; r,t; :m: '*~
..,fi~ £! f.t; 'mf: rr.nril ;ft:8 7'i"ft t I F' ~ ~~i
r-Hl} ti ~~· mr. wer ~ g:;ri wr?f: f. fiJi mit t*m
;r:tt ~ , ¢;-'<m ....t yuri ~ m arm~~ f).~ •
;)1(1 ~} ~
L 'ttl>' ~·:1 2. IFl/ d~'Jrf
J.. if:R ,..-Jf 4. r.;tlllfl~
I . erri! ;.;.r& ;:<)1<1 ;6 q=l t a!if :::r-ft *~ff, f.1 ;,;m; F
2. ffTi"i c;$ t:~r.s tt~ ~ E «of qr-;) if
'i~r;f;r itl vmrr t
3. ;.rrt.r<t·;i rrr:.:wf ;nN ut;! <GT fFWi m: Jltai {:
4. <Jii'mlt' t(f{;' ~ 1j<: ;r(f rm~
15. ;;,'J~~ ftrn i{ t:r,ki JtJ'i1'7 fff( rt't?<!'tl trn
A. B. C •il7 D q <;w J!Rll m.R !J1fl t 1
:t•h.'/} :.U(J ti; ?f.!ffl if fi!rr.:! if W(fit="(ffl 1/KR mft
t•
I.A m;r;rr(Y( i! IJ'~'W up; ;;;rm. 8, C. 0 J1kR :f1
2. R ~ ~ tp.;"J,- ~ ;r.;m A,B, C .J<~Df1
3. n>W1fi11i t 3m~ elY, !tr'f(tc, s.A 3)''?' R ~·~
~.A it"'~· f. :;rn;/;W.: iSf(t,o; R, 13. C #iY D tJf
6
The spring balance in Fig. A n.•<tds O.S kg and the
J>an balance in fig. Breads 3.0 kg, ll1~ iron bl()l:'k
suspended fmm tin:; spriJ1g, bakm::c is pani:tl~y
irnmcrscd in th:: water_in lht:: be.-.ker (Fig. C). The-
spring b:tbnce now re~s 0.4 kg. 'fhc rca.ding on
che- pan balance in Fig. Cis
I. 3.0kj; 2. 2.9 kg
3. 3.1 kg 4. 3.5 kg
J3. TI1e ends ofa r(l~ are fixed to two pegs. such d3t
the rope r~mains .$lack A pettcil is plact'd ag:Ainst
the rope ald mo·~d. such th:Hthe rope always
remains taut. 'fhe sha.pe ofthe curve traced by th<;
p::m:il would be a parl of
L a cir~l¢ 2. ~~~ ~Uipw
J.. 3 square •• a triangle
14. During ice skating. the blades of1hc ice skater's
shoes exert pressure on the icc. Ice sk<lt:.-r can
efficicnlt}' skill¢ because
l. icege(.S <:on~·encd lo ~i~c as ihe pressure
exerted 011 il increase.~.
2. ice g<:ts convcr.ccl to water as the pr~S!:>utC
CXC11Cd Oil it d~crt'<ISCS.
) , lhe density of ice ill cont.'lCI with the bhdcs
decreases.
4. blades do tlO! ptlltlrate into icc.
15. Four s~'dim~ntruy rocks A. B,C and Darc intmded
by :t.Jl i.greoos ruck Ras shov.·n in the cross·scction
diagrum. Whichof the foiiO'ing is corroc:t aboul
!heir ages'!
l. A is the youn~est followed by D. C, 0 and R.
2. R is the )'Oltngest followed by A, 8,C and 0 .
3. D is the youngest followed by C, D. A and R.
4. A is the youngcs1 followed by R, B. C and 0 .

7. 16. ""'"'" ""~' """'"""'" "'!I' ~ t ~.,.fi<1r.1 /In h~ ¢1 '1"/t I
I
~
Stra.-.-
I . !imml ~ ""' i!ffl Jfi'QI'I<tl1f'{!/;r; fiPijir
.mrt 1
2. /ilyrrt17 fir~ If<'"'" ,..ht:>f,,"""~,..,t I
3. fJlwffm Q:;t w Wa JJPH p #:PNf • HM ...,
Jt(1 r:rrm t ,
4. RVJMfff r.H ifl cs>u r;~m -.~~ {q<IJCf t) rirlffl
t I
17. <"viiHit >(): ~ Rl 'Wr't IK f.l•it >iimfi) <a
Wli1f/1 r;t;1 ftl :fti It;} ~ !iF8 if t:lfit:1 r;:zi t I
,., """ il """' ~ ....... , '
:II
I
•• ..
) , <:"'tl'~ ftoT ~ .J.'fflW'R
2. 20 >I R~
3. 20 ..)0 ~ .. ""'
4. )03 .:0 ~ill '*'
18. NT« (R) >1/Jf/ or# r:<n <f,) (T) r/IU (1MTff19
~i+·~tmlt) at f'1i rttR (r) 1fr.it ;:m .W:t (t) ifh)
?t ~ t';i;1f1 rr.t1 P..7 J mt ~ ffrmt ;t
fPWI fl/f!ll11 ~ r# tva :s ~ fPI;:: ~ W:r t);tJ
"' ;pi$ . , . "" ""' ....., ""' , •
J. TtRr x TtRR
2. 'J'Ur> urr
3. TTRR• ttn
4. TTRR x TlRr
7
16. TheS-train iJl a solid subjected tocontinuous stress is
plo«cd.
I
j
Strain--
Which ofthe following s1<ltemcntS it 1n1e'?
1. The .!tolid dcfomts daslically tilt the pomt of
fadun:.
2. The soliddeforms pl...,.,.uyom<h• point of
failu~.
3. The.solid comes b::k to onjpnal sh:tpc:3nd srxe
on failure.
4, Th.c solid Ispemumentlydcformcd on failure.
11. Growth ofan orpnism was mon1tor<:d ac regular
int.ct''al$ oft~. and as ~-n in &hi: graph lxlow.
Arotmd ~C'h lime rS me rate ofgrowth 1,1:!0?
l!
I
.,
I. CloS<to<by 10
2. ~d.ly20
3. lkf9.-un days 20 and 30
.:l. Rc1v.•ccn da~ 30 and ~0
.,
IS. A 'IOU pla.~n widt Hi!d s~-ds (bolh dominant lntils)
was C:COS$ed wich ~ dw:nfplant w11h wh1tc seeds. II
1h.e segr~g:uin~J p:og-~tny p1oducW cqt.~3li'umbcr of
ull nxl and d--.-;wf'whilepfanb.."h..t -.ould btlhot
::}."00t)'1)e ofthe p:rec:s?
1. 'ftRrx T1RR
:2. TtRrxurr
3. TTR R. )C ucr
4. TTRR w·rcRr
_____}

8. 19. dJ:-, 1f!fdt rf.lh ~ ~ <:71ftft rn:i Q~JflmY if
'{ffl If#/ fiT
qr.,A . f:trn< P'7 't
~":! B; ~~ flr-i if ~7i.i n; ~
~zrC : J~t.l? l1 ~ 1:81 q
I. Q'h-i B 11ft WT~il7.''f ~ > ith~ A
2.
3. 4'iti C iJl QUUV"!' <:7 .a. rfN A fi'O llll'IQIH
<'
-'· ~ C 1fh iiiu..rw.l <:i" > ;f;$ A fft WlN?H
v > *'0 11ft qji/(4(;'7 "
• •
•
•
I. a., aidali+ .. . =<d(l-h) for !bl<l
2. a > b il mlf'fli a!. > bl
J. •(tt-hr u-'l + 2ah t-b1
• a > b ~ dk<fti -a < -b
8
J9. "Jlvte sunflower pi:m;swen: plaet<J in co!tdiuon!> ii.S
indicotod below.
Pla.nt A : stiU air
Phtnl B : modcratdy turbultnt ~.lr
P~t C: at~ll air in the: <btl:
Which of l.he following stncmcnls is ~orrt<et7
I. l'ranrpirtuion rateofplanI 8 > that ofplane A.
:2. Trat1Spita.Hon rate orpl3n! A> lhatofplant B.
l Tnanspin.tion r.tlc ofplant C • tha1 ofpiwt A.
4. Tr.w.s:pirotion rt.t.e ofpl:snt C > IJwt()fpl~.nt A>
"'" o(pbn B.
20. Which ofthe foltowing i!> indkutt<t.l by l11e :~ccom·
,onying diagram?
• •
•
•
I. a +<1b + ub' ., .. . =al(l-b) for lbl<l
2. a> I> implies a3 >b3
3. {o•b)1..ol-ltJb Tb)
4, a>b implies- a < b
•

9. 9
[ 'I7'T B ) [ PARTB I
'
21. VfP: 'MATHEMATIC$' <6 .mm' It U0Tm1 11 lt.
.~ m<: ·~It) Vfl "'"" If?
The number or word~ chat can be formed by
pcrcmning the letter$of 'M/TIlEMATICS' is
I. 5040 2. 4989600
3. II! 4. 8!
22.so.ooo..- ,,_~ 1'
I. 20 2. 30
3. 40 4. so
I. OJ7llt (ATB) =..tit (A)+ V11iil (0).
2 om'i) (A+B) S tV1fi) (A)+~ (B).
3. 01/li) (A+B) ="l"'!"{...mt (A), 0!1l.l
(8)).
4. ~ (A+B)= ~{...mt (A),I1fl/il
(B)}.
24. 'IT'/ ,.
n .
I. 5040 2. 498%00
J. II! 4, 8!
TI.: number o(positi~ divisot5ofSO.OOO is
I. 20 2. 30
3. 40 4. so
Let A, B be: nxn 11~01 m~tric<:s.
following statements is correct'!
Which of the
I. r.lnk (A+B) • mnk (A) • ronk (B).
2 rank (A+B) S:nmk(A) .... rank (8).
3. rank (A-B) • min {r>nk (A), rank (B)}.
4. rank (A•B) • mox {"'nk (,),rank (B)I.
24. tet .r.rxJ={'o-"" forxo(0.11nJ
for x"'{lln,lJ
{
l-nx
/.(.<)= 0
forxG{O.il nJ
for xo{ll n,lJ
ffl rnen
1. limf.,(x), (O,I)'IHimr"""" 1111 qfNpn
·-
I. lim f,,(x) defines o, con!lnuous fimccion on
·-·(0,1].
llmfl i I 2. {/.,} convet~ts uniformlyon (0,I].
2. (/;,}. (O,I]~o'7 q4'i'd'i,., ~ 1'rlff t 1
3. ~xe[O,l]<t .I>' /lmf.( xr 0; 1
-4. Wxe[O,I] ;f; ~lim f.lx) l1f1 ~
·-
3. limf.{.T)• Oforall:r, (O,lJ.
-·4. limf.(;r) e.,isu roullxe[O.I).
-
1 I
25. The number .fir•s is
I. qf"#1;f 'ff~ t I
2. ~frl
3. ~mrme,
4. ~#0211~ I
1. a rational number,
2. a tronsccndcntal number.
3. an irralional number.
4. an imaginary ''~unbcr.

10. (~-· Q)Aa .
0 <;
~ ,.=('•'':,v,)c;:i' ;t f5ii 1'"1, ,r, ~
• 'I ''!'""""' ........,.c· V vAv ""<"' " , " iF.1 '•J(·:;r: t' I :Nrn w •
(l.l.l)ill!w!,
l. 0 <i: 11'l1'l F I
2. 1 ~ iPlr-1/ I
3. -1 "' '"""' I I
~- 2 * (rr;pJ t ,
I
10
26. Ltl (:bea primitivecube rom ofun11y. l)etine
For :a vettor v • (v1• v:. "'')<(~'define
l''l4=Jiv,.h•rl wht-re••1
islTan:.~ufv. I[" ._
(1 ,1,1) 1hcn w1~ eqtt:tls
I. 0
l . )
3. -1
<!, 2
27 .rrr~ ii5 ~ - i(a.. a:. a)): a;GO, 2, ,1, J},
a1 +a.;=6}. M ~ ~NIIJt~Y't/J~ if~'l I
3 1 + Zi . Lt:t M - <(a1, a!, a}): a;t= P , 2, J, 4~. a1 + a:+
3}= 6}.'fhcn lh~: number ofclcmunt5 m M is
l. s
). 10
2 9
~- 12
28. (38)'0
" q;r :J.'til>t >ilK~ I
I. 6 2. 2
J. 8
29. <1¥P./2ih ~ ~ 'f"~""'""n(n~2)
q,'fe tl~ 'fPo' ?r~ 30/d/ft A- (a.•), n11 .. 0 It
~'11 11'#;: ~~ fiN! t . .
(n1
-+n-4)!2 2. (n2- n+4)1l
3. (n'+n-3)•2 • . (n'-n+3)>2
l. $ 2. 9
3. 10 4. 12
28. Tht: I:L<~t diait uf(38):o11
is
l. <) 2. 2
3. 4 4. 8
l9 The d~1l110n orthe ..-c:aor$pac(' o(all S)'tl'l:r.r~c
munccoc A.,. (a,-.) ofO'l'der n)f;n (n ~ 2.) with real
cntncs, a11 - (}and tmce 2cro 1S
l. { n'•n-4)12. 2. (n1
- n+<l)l2
3. (n
1
<n-3)12. 4. (n' nl })ll
JO. '"~ f.k 1 ~ (O,qc::< 1 x<?. .t flM .,.~ ftlr 30 let I - (O.I JC:<. foe- x~::<. 1t1 'l(x) = dis•
o(.x)= :;,It (x..l) " tt"""'" {tx-y!: ycl}, n> (x. I)= tnf (llc )' : yel}. 'then
I. :.:tY? (o'JI.t ~X) .fmffCf ~ i
I. o(:<} i:ldisronlinuousiJomewhct'C ~·) ·(,
2 ~CR 9(x) r.mr f. "FIJ ~-m:; x = 0«1'
2 9(Jt) '10 OOClliUUOUS 1.)1) 2 but llOt ~l:llliiiU.CtiS!~·
"""'- ~ '1'.6 I ' diff4.-re!'lltab!ee.ualy3tx ~ 0.
.l. ~W o(x) ~ l 'ff;J lR;Xtt.~ 't., 0 ~ x., 3. Q(x) lS IXIOIIUUOUSon :::_butno1
l W 'H."f(f ~~Nf·f:ll 'IJ;.": # 1 <:Otl1ln1.1<rli'IY dtffcrcnlr.~bfe u .,cd:r at x-
4. ~'IT l,'(X) ~fh.· 1..~ I
0 ilnd Ill .X - l.
• <;(x) i$ t.liff~.:n.~u:i:tble on R'·

11. 11
3J. 'TiFf fit; a.. • sin rt/n I JJ;7f a~. a:.....,t ~ Vf:irq; .3~ Lot:In • sin ltln. For tnesc:quencc:.1, a:,.··
I. 0 t U <1lf R1'<r ~'tlrT t I
thesupremumis
2. 0 t 'I ~ lll'if'J{i iflm I
3. I f'lllf1R'lf#m/ I
4. I !. • q 11/Vf '1tf f!Ru I
l. 0 Mel1t isanaincd.
2. 0 and11 ;s noc.aua:incd.
3. I and k isaltrin:xl
4. I and tJ. is not attained.
32. Usin~ chc fl.ll:t lhat
-t- 1
"' ~ 1 , cqu•ls
f;,r=6· ~(2n +l)"
,. , I
I. 2. :.:....-1
12 12
I. •' 2. •'--1
12 12
•' '3. 4. ~ -1
8 8
•' •3. 4.
.:!.__,
8 ij
33. 'R'f fit; Ax.y) • u(x,y) ~ o,~x. y)n "" I'"' 33.
~ """'f: (-( lj I
l<tf. t-C b< • <O<q>kx >-alued funau>n or lhe
fomofi:x,y) • u(x,y)•; '~'· y).
Sup~ thOl u(x, y)= 3x1y.
'llfl IW u(x, y) • 3x1
y, 8)
I . ("' v '*I'GiiJ >fl ....T ""I ~ <(./
i.liT'R11 I
2 c.,. y • """' - 'RI t<l><l~ #'7T I
3. (({f v <8 ws8 rmrr wJ t=)?.lOJiMw
;!twI
4. u IW1iii<T•flq 'f{f ~ I
34. 01'!' fit; f: il<' X :<1
-R ("X fii/fGtl1 •fl!fl;7 t.
.,.;iq 8'f •• II $f(f1 if ~ t 1 m(V, IV)
e!?.:' x ~~- fir# {H. K}e:<l x ~~ tn ~"it
.,...,.,..Df(V. II~ f.tGr <9 R>.n """ t •
I. J(V, K) ·•/(H, W)
2 /(H, I<}
3. /(V, fl) +/(W, K)
4. f (H, V)+f(W, K}
3s. .,...-.,., ) ""' 11711. ,..;; ""'R"' arm ~~~t
>;R-n ~ N '""' 011') 1 S: N -N 1lfl ~
# (SpXx) • p (x + I), peN 1 ol (1, x, x1
, x'l
ViT ffP,~ ~ v} fiQ 1f f.. STf 31/UI"I .;• 5 1fiT
~ ro lliKR ~~~ wmr i :
Then
I. fcannol be holomorphtcon( for ""Y <h6it<:
orv.
2 /is hobnorphicon C for a SU1ablccboitt of
v,
3. /is holornorphic on (for 111!1 choices ofv.
4. u i$ not difTeretuiablt-..
34. Lei{:: 2: x R~-R. be 3 bilineo.r msp, i.e.• linear 1n
ach Wb~ ~kly. Then fot (V, W) c;:3.:
x :~:.the deri'36·c 0 f(V, W) c'lkl3:ted on (H.
K)E~' >< R:1
is giva~ by
I. f(V, K) +/ (K, II~
2 / (II, K)
3. /(V, H)+f(W, K)
4. /(11. V) ~ f(W. K)
35 . 1..c1 N be W v«t()f Spaceofall m1 pol}-nomiaJs of
degree ot mos13. DefUlc
S: N -·Nby (Sp)(x) = r>(x+ l), peN.
11ttn th~ m:;l(Ci.x Of S in llle b:btS p, X, X~, xh.
(OCStdercd os ootumn tt10t'S, IS ~vcn by:

12. f1 0 0 0 I I I
0 2 0 0 0 I 2 3
I. 2I) I) l 0 0 0 I 3
0 0 0 ', 0 0 0
I' 2
~l
0 0 0 0
I 2 I 0 0 03. 4
l~
2 2 3 0 I I) 0
3 • lj 0 0 0,
36. .l(l'r.'' /#1' r.s ~ ;mr. tf-t~~ m 1 f!ii.A •lxeF
x:::: t :r ~.-1. k < 1 m m' ~ ~ <t
ffi.·) JI H) A ~ J(:tr;t'il> •If! <H'Gtli t :
I.
3. 3
...
L; :S")
2. 2
•. 6
2. "'<,I)
4. ~~II £ J5
38. "'100 • 01.' ;f; .,. • •'nm ""'Q c ~ l1f'170
r,_.f/M "II rf~'?li{1ft ~ 1 I fl /ill R ~
EJ"';f(.~t,p fr~J / I u>'Mf :Jf!,Q 11 i1i! I("$ q.$1
<Pm!Jffm t?
3, t:"r fR'f) J.~ ~ 11fl Jt,ciiW>rf1 "lf'if t
4. ili'ft '1t.1 I
I. I(X) ~ S(X) .n>(f'CI"f/q t I
2 l(x) Jf«;<t>?"T• d '''-g g(x) o!/1 '
3. &'(~) JiS!jitON::t ~ W'!7 1x) :rt:· 1
~. ~ fR I(X)Z.V. 'f ~i g(x) .,;(t§a;'llf,zo t I
12
I 0 0 0 I
0 2 0 0 0 I 2 3
I. 2
0 0 3 0 0 I) I 3
0 0 0 4 0 0 0 1
2
~1
0 0 0 0
I 2 I 0 0 03. 4.
2 2 2
~J
0 I 0 0
3 3 3 I) 0 0
36. lm Fbe: fieldofS<iemenosondA • {xeFJx'=
I and x'~l foe :tfl n:nur•l numbtrS k <11. Then che
m• mb~c ofe!em..:nl$ •n Ais
I. 2. 2
l ) .!. 6
37. The powtrscrie11 f J." {z- ti "COilvccges tf
I. ~1~3
3. ~· II <.J3
•••
l 1:1<,/)
4. 1:-IJSJ5
J.S. CO:'I.$Lder L~ groupa • tb'Z ~o~,·hc:~ Q And zare lhc
i.'J'WPS ofnu.ioo11 r.umbetsandinttam
~tively. Let n be: 01 positive uut"et, '0en is
there l C)'clic linhzrour ofardcr n'!
I. na1 ncccs.s.srily,
l )'(S. 3 ur'l~ Ont.
3. )'H. but no1 ne<CUMlly~ urtiQUC' one.
~. n.wet
l . f(s)and s(x)tarl!' irrt:duciblc
2 ('(x) isjrr~duc1blt.:. bul &'(x) is noa.
l. a(x) is irreduribl~>~. but f(x) is noL
.;, ~&her f'(x) norifa.) rs lm."dcabk

13. 13
40. Zc1JJ " Zut) 1r.. <t &!Ji9 il&17 "6W>Ji'ttu <1ft 40.
'l16IIJ , '
lbc number o( non~cnv1sl ring hocnomorphjsms
from :z.,,,to~ is
I. I
2 3
3. 4
4. 7
41. flldilor '"" - y'(t) =l(t) ) t), y0) =t <m
r: 111:-11""" t .. mm 1m;u-~"'_..
I, 'fjf1 1' iff fM "'""'' liS"ffl t)d i! I
2. II.. 1!11'. ,tl'l Smt t I
3. R 'lr 'IJU ( Iii 1M 76'1'! l[H 'ltl E1oT 1
4. o1.<1~ ,;1!11'.;hroo; ii ""' m
m t <1RJ 'IJU f Iii !itt R.,. 'It/ 1
42. '!PI Ia. ""'"".,_ w>II<>Mu"(t)- 4uXt) +
3u(t) • 0, t •li< ill w<li '*~ .,U.., ~
v 1 unv
I. la'll 2 rtll Vl' 'lf!l'itf# .trn wrl<i: t 1
2. f'J'IJ I rt/1 Vl' rmrt~or .trn 'l1'lk t I
3. 111'tnt VW !JfU r&((it u=O rrfJ 3P.ffif;:e iiRffl
t I
4. lfl>r-5/i/f 111 t/ """";r;) 3Rifil<: l/m11 # I
{
I -.••
~fie" . r>O. xe IR
43. "'""' u(.•.t)• 01
.tSO..reR
~ w>f.!:sftl' 1lf1 p,,., JrifRm ~ ~ tt:i.:f t :
I. ((x, t) : xER. tG~}-
2. ((X, l): XE:i, l >0} <TRJ ,....""'
((X,l) : XG:i, t < 0}0 'It! I
). {(x,t) : xER, tER}{(0,0)1.
4. {(x. t) : xeR, t >-I}.
I. I
2 )
3. 4
4. 7
41. Consider the )nitial value problem
y'(t) • f(t) yt), y0) = I
where f: ~-!R it: continuous. Then this initial
r..luc problemhas
I. infiniccly m3ty solutions for some f.
2. a umquc sofuliOn i.n !.It
J. nosoluhon tn R forsome f.
4. :a101uoon in o.n incerr.al(Ontainirrs 0, bul not on
!Horsomo (.
·U.. Lc1 V belheset ofall bounded solutio-:l.Softhe
ODE
u"(t) - 4u'(t) • Jl>(t) =O.t <::!
Tllcn Y
1. is~ rc::.l ,·ector spa~ ofdimension 2.
2. is G rcaJ 'CtiOr Space ofdunc:n~ion 1.
J. conU.IUl~ only lhl! l'rivit~l fulction u=:O.
4. comainsexactly two functions.
43. The function
{
1 L
-,.,~It • l >0. XE IR
tt(X,I): ,JOt/
.tSO,xeR
is o1l ~Judon o(lht ~I eqwbon in
I. ((X. I): xGl, teR}.
2. ((X, I): Xf'!i, t>O)butnotintb:sct
l(x,t) : xol. 1 <01.
), ((x, t): xeR. tE::!I((0,0)1.
4, ((x,t): xoB. t > - 1}.

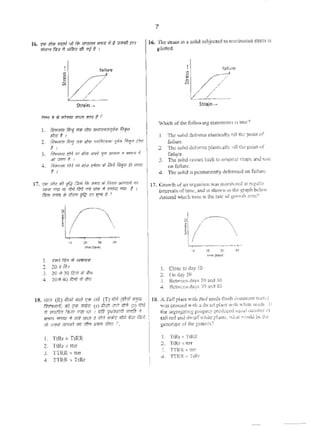
14. 44. 'f!dt ff:}f~ tf, J.'ifii<n 3,'11"11 ~4F&ro
u,. yu., ~ x'u= 0
#
I. ir.Jl XG~~. y~Jl ;j; fir.) ?i~a ~ I
2. ~;;I} '<ti ~. yeR 1$ (i:td VNC'ffi:;</; & J
'3. ii".:t x~ .i . y <0 lr" .Qrl) E:t~ # I
4. fr.f} XC l'(. y <0 mftrll ~"' 1? I
45. <;!ifi q,t.Q ;)'; f[f5 ?JM7flf st7•...,~r lr4Pir'i~ ~
~ ~ SG1 ~ rl tm ;; fJut~ I ~
.. fl 1'"' fi<~ <l>'f'l IR q;ll1'f I
I, olfl/1)/f ~ i~Uf J(iR1 F !
2 T!f1 " " r.ro~ fp!r.1rfQb"' J; [;?rt u."'flrrr
~~Ji'FVt~ I
3. """"' - ~~ ,;; ~ ~"""'
~.Yr'R ~ ~ # t
4. qml'm sffl Jt(i)?flvrtrr wl Ji'~'" l.}ul.'m
lfl·ft tt) U4l(/t I
I
/ (vi<)) • f, y(3x -y)dx;
l. '!fll JFRI Mi f.tm f. I
Z >fl.,_,.?) tJ 1!<'1 p:?il (! I
3. .)('<'!~ rrGIIT if'; Fl' .-Ill # I
-'• t/i~ Jl1li! liifJ ;:1;J1 I
47. <ib•> ""'""' ~ ;ix)=.•~ [ '~(C)d(.
••
'11 lffd flf.J'<P J>'k R(x, ~; I) f ·
]. l"l
3. ~tl
l . 2
•• 4
14
4-4. The: ~coond otd¢r I' I")E
o, - yu.. + x'u 0
is
l. ollipti¢ fo~~ll xG!!L ye~.
2 f!3rn001!c tbr all xc3, yc::::L~.
l . cU!pltC for all '(fl 'l.y< 0.
J . h)'J)I!'rt>ohc for:all xeR, y <O.
45. Cons,(kr a second order ordmary differenu~J
E<;'..,1101'1 (00 l:') and its finite difference
rqxnc:ntabon. h.k'ltlfy '4ilich or dte folloo.:mg
StOlCMC:IUS i& CQIITC'CI.
t. ·rite finite (li(f¢tCJlCC n::prcscn1n1ion is unique.
2 !'he flmtc difl(fcnce represcrHJ1101l is lniquc
(or son-.: 001:.
). ·n-.m :sno amquc: Cimlc dttT:m-.c ~ foe'
th~OO£.
4, 111e UOiQllCilC~~ of~ finite <hfl!:l'CII{CScheme
enn no1be d::Jcnuincd.
46. ·1he nrra.;::omJ probkm of c:dn:mrA.,g the
funtttooal
l
l (y(.<)) =f. y(J ' - >•)</.<;
M.•
1. :t umqoe soluuon.
2 exactly tv-·o soluuons.
J, nn ullinilc number of !:>Oiuttons.
4. no solution.
I. 112 2. 2
J. 312
48. % tt!frrrtm fr'i $t ~~ H= pq - q~ tt omti 48. If du: J[;un.iltoniatt ut'"a dym:micai•)'Sterl is given
f.(,') iUI! ·-. by H: pq - <l·. thc:nns t--
I.
""·
'••
4.
q- - .p - (10)
4 -0. I'- 0
(( · ~. p- 0
4 - o. p - ~
1. q -· <».p- 00
2. q - o. p- 0
J. q- -.p - 0
J, ll -(l, p --

15. 49. ff<;41 t;::r o;wr F,(t) >r F,(t) r{1l rnfir.lmr """'
'"""' f,(t) • f.(o)$ ol - WT, • T, oll
;:f:i&"( ITftr;!j/ iJ;tm; )l,(t) = 31~ II h1(t) • 4~, 1 >
0 C I~~
1. .,n,> ottl f«ii F,(<l~ P,(o).
2 !70h I> I ttl /i;>1 F1(l) < f.(l).
3. E(To) < e(T,).
4. w>l) l > 0 41 f,rz) f,(l) < f,(t).
SO. "'" /tl X,, x,. ... o~1, 1) <6 3fjm< mkr.m
W<ftl lW 6 #til t.,t'J2NI "' { I 'li'l It; o ~
!.P fi:rd S • X,l+X!+···+ X~ -' 1 ;r)
.. - " ('
g1w:(S)
lim ... .., ~ t:
_,.. ll
I. 4
3.
2. 6
4. 0
51. 'fP. f.N {X,,:" ~ oJvw 'lMitH Mnon ~tifh s
'R ..,., 7/ifj"'f ~ 3l"''J! '""' ""' 'fl18lo
.;.,., t I ...~ ~ fWifl JRO!f- 1t.l f: I
ffl ~ rrr.r.'frr ~·l!IFtT
I. ,f: Jf'f<Kf' lf§if '({f'U ifc.t ;ngt f. I
2 <1>1 ViG A .jpRI '«16{ tk:"-t ~/fiJI 1 I
J. 01!1 oat ># """' - 11$1 ·rt!l # I
4. ;t U/q;- ;JM l:t fffN dc-r JIII/I ;rtt 'I I
51. 'l1'f f!t; X • Y <I - ~ ., #. omO>l
&-ff fff'lf Y Wl~ 8 I lfF'I' fi5 U= X -+ Y' lJ
V=X- Y m
I. U >V ~''""'' t
2 (JJtY ;it-~~~'fPrRt I
3. U(P)m O;l o:T-ff <fl'll <1'111rtf d I
4. Y KlknorteAiiff'II~Z I
15
49. The ~~rd rates of two life time 'tmbies T1 aM
T1 wid' respectivt e.d.r..s F,~l) and F:(t) and p.d.f.s
f1(t) and f:(l), arc h1(1) ~ 31 and h~(t) =4tJ. t > 0
ccsp=ctively. Then
l. F1(t) l' F2(t) for sll t > 0.
2 F0(t) < F,(t) fonll t> I.
3. E(T,) < E(T,).
4. fo(l) < f1(t) for nll t > 0.
SO. Cct X,, Xz, ··· be: i.i.d.l•t(l.l) random VJriable$. Let
S.o:-Xf•X:+···rX~ for , ~ 1. Then
limYar(S.) is
_.,. II
l. 4
3. l
2. 6
4. 0
St. 1.<:« {X.. : 11 f! 0} lx: :a. M:nkov ch::un on a finite
$talle space S with Jtuionary k:imkJOn p«)bobility
n'-11nx. Stpp<>sc: thm the ~hain 11> nQt
in-educible:. TI1en the M:ukovdta.i1~
1. admi1smfinitclynl.,nySt:llion:trydiStl'lbutions.
2 admits a unique ;iii<Hionory dlstnbution.
3. rn:aynOr ad:lua anyst.u.omry <b.suibution.
4. cannot:tdmit (:103Ct1y two smtiV11al}'
distributions.
52. Suppose X 2nd }'.ve ind<:pc:ndent r.u1dom v.'u;ablcs
wh<:reYi~eymmc:tricaboutO. LetU=X-t Y and
r • X- r Then
I. Uand Vare always itt<h:pcndent.
2 U and Vhotve &he- ~ncdtSCribution.
3. U is111"'li:)'Ssymmetric about o.
4, Vis a.IWA)';ii SymmetriC #bMII0.
53. <:0 'g'llit ;; at •r-f.lt11<w "'" 'II flfil >tm!llrT>ff ;f,l 53.
""' 11/) ~ f.;r.r 2:oa mGm # ~
~ t; :rdJ t 1 ~ "~Pr-r $) rrtr'fli~ :
6,nsider the following 2 X 2. bble O(froque~'ICi:es of
''OC.·cr prc(en:nt"C:S to "''0 parues cbSS.~fk"d by
l_!Onder, Ill :ill election. IdentifY lh~,:: CQITCCl
~t<ltcme-JU:

16. 16
..-rT ttl'" ~ ff.:p. .:e e-c f1fJi m ~ t m
~ JOYV-flJ..J M,
ISO •:zo
120 280
2 -,! Tf &·j'flfktfa <5 tm:m ~ mt rl
·-:f:'t<ffl-.r. 0 f, I
3. {~ot </ Wl mrf!m :;fF t :
4, !(H J fil ;;'f;ff ~ r:t~ (' $t ~ ~i't
;' I
$4 t1'l"'f fir.':• •{·,···.X. n (~ 2), N(p. <1:) R:r1 ~ 54.
f1Jt.~r6q tt~tG '{;(1 ~ ~ ~1"1 ~· ij"'f-#C< p
... -'11 O<o:<r.J..'ifm~? 1Jfm",f!J;
.. .. .~...,___ _...._(7' , ;; IJ ..,~T F ~ C' 4) SC07~c~<f .,...,,JW.H fl
tr,.-,n;pf 1j,;r,J'"i ~ ~$';7ft J/!4ot<( ~ / Rll
" ¥~~~-) :
0:1;, ;:t;i 'f1'7RV! (jl~.fl'l./C ;6 r:?n"1 r$ Vf11N
t I
2 a-~.,1{'" ;7f) gM.,l tt u;l,b ;r.r .rrm~.JI'fhvr
F I
3. 6/11cr. <Iff go?T # U~u. tm ~ li'! 'tllr.
1$q $ I
4 a:.r:;; u(2
V11'£ m· <t j~ .:rf 'liW ~q,..,
• I
55 "'"' ,. pet - x..x,.···.X. ""' """""" <17:~ 55.
liM PrliH'f Mtt~ M ~ ifRrt t-~ j I ~
~olfr 'IT-t' f); Plf{ qro fit) JltrYf--"'' m llJj;?
rwv ~lf'lf ilfFPl r,. r!····.Y.. '" I w~ -41
mivrrf'J ~~fl W1Jfi:l/ f. I ¥Pi' flJ; 1(1• ,. X 'if
r 't.l"'>~ !fP'trr 'H'J'Qfa :!f x~; fh1 :~(lli'Pr~ rt"'t)
1,•11 ••,,,,v.N ! v1f R) =gli1rt 'H'J'"•'~' ~· y,;lf} t~>?
;;;~tlit1,·t •hi 1;)rr~ ;.'t t rt)
I. P(llr-Ro·> Oi> .!..2
2
I
P(Rr-Rx>O)> - .
2
), E(Rx) = E(Rr).
·'· P (Rv ~ Rx)= l.
I. Iflhett is no 'USOC'latiOn bet"C¢11 patty aod
gcoda. ~ cxp«ttd fr«qunnes are
ISO 420
120 2SO
l The chi.-!qu.are Slll115bC (or ll:~tlng no
3 SSOCilliOil !SO.
3. Gend-er and 'part)' are not a&,Oclatcd.
4. nolh m::~1es aJld f.:mulc.s ~quaJty pn:fetpany c.
Lc! X;, X:.···.X, be n (~ 2)11.d.oh!>eT'tniMs from
N(f.l. a~) distribuliOil, where -crl~ JJ< cca.nd
0 < q! < :tlare W'l~'n puamc;ers. let
U~and Of.,.(,.,. dencMt the nwimum likclthood
3:n:d urut"onnl)• mmtmum Y.Vlanet u~
tsiH'lltllesof q: r~pt:11~l)'. kttcnllfy the corr«t
stateu.ent:
I.
2
3.
4,
U,~t~l.' hOl$ th¢ S8nl( 1'IMIJnCC :1$ that Of a~'IM/~,
cr.~tt.r. ha:o taq.ocr v;ltiu.nc~ lh:m '""'(II' q~"'1.'!• •
a.~t;,c has smaller meansquttrcdcnorthan th:r.t
Of 0}.411OJ!,
.... . ~
<T.~tuand at~,.., ht'C the !t.mlc mean squared
mot.
S~ 1!!11 W~ h'ne ud obkzY.b>nS X~o X."- ••••
X. with z notm::!J d1$tribut10n. Suppose fUrdlet' ~r
we h::~ve M indtpenlknt Ul of obsef''~tton:s Y1•
Y:.~··.Y. which :~.re :ll:£.0 i.i.d. wnh the sam.: nonn~f
dis;ribution. l.ct R,1 • th¢ !ium of 1.he r':lrks of the
;r s when they are ranked in 1hc combit~cd se1 of X
aud Yvalt.•es. (!f'ld Rr • lhC.sum ot'thc rank$ of the
r~ iu th;; COJlll)ittcd ;)CCI. 1111.)11
I.
I
P(Rx- Rr;;. 0) >
2
•
2
I
P(R,-R.>O)>-
2
3. E(R.,J=E(R,).
•• P{R.,. = Rx}= I.
56. ('#/ ~!lllf<lfj il'flsr.P: Pt~'lf Y e p X+c w
f.l7!tl 1 tff.j f.t; i9 , X.:::X<~ '17 ,, iltrvil'(Y11 ~). I
56. Co~:asider a simple linetlr rcarcssi<1n:n<Kkl
• 1.... ,. u x=.!.f x, ~ Jllflrfitt r ",. ,._,
"i""" 11'1 ll1'WffT t I i!T I1l"'<!ftt Yo till .....,...
JR
t' = /)X+t: l.c:t ~be lhc lc:.~st liquares predictor of
Y 3( X • X11 b::~sed on11 observruions (Y.. ~Y.). i = 1.
· d X- 1
~"...,n an = - L"'''
11 (R1
Then !he $tanda.rd error ofihe ptcdicOOT ~
4

17. I. ;;rq XWXo F FZOf 't ffl iStf itift t 1
2 ""' x'II·'•'l!..,t m"'tiroq#t,
3. vm0 a} W'6 x0JiTW # fit 3ffW; Etcf1 t 1
4. VJ4 0 zy qro ·'Co MFfF t 8t <1J7T irift gJ
51. ~q;; m r1 I, 2,..., N ti&JI41~ N ~;J;? Jhffif'Z
t 1 N <6'1 1J.Rf mn~ .mrm t 1 wW ~· Wwrm
m fir.rr rt<!i immVT ?if'ii~ n ~-if WI
f!fit;rW ftt/;t;m1 1
flJT 1 '!R fW Xto X!o··.X..
~..r .. ~ .w mwr t VJt iSm m. ~
..·• n i' i1R f.'rtliffi' *' rntJ vmT : 1 f.!rr.r fi 11
m N wr:;,"'lf1ffll.,.,., t ?
I. 2i<-l "'* X;~(x, +.....,x.)
2. 2X+I
3.
- l
2X+-
2
4.
- l
2X--
2
58. ..- ~ >il ~ R; = ,) """" wl J!llq A q
8 """' r#r( '" ~ ~ ;t?t f. 'f'll il<7fil<>;
rr1tem ft1i1n >trJt ~ mt;fcuu> nr~ W yt n
UJfilfr r.Tflli;r R,-i/ •W I i!llq A P UJfilfr >il
~ <'<l' <) '!fll 'Tllt 'f'll !I"' it """" ""'
ll itiP/ B rub ?fi'1 i; I rrR' fi5 :fN) '1i7ft
WiifJJ41 f((1i mm m f. 1 ~ tJt rrfiWl t!J
fitm ~ ~ '1l1 ""'"" W{7{ orft:iJ ?
1. 3f1R JHwn;;qm 1Wft ii!T YT<Iirft c·m~
- flftrrn ;!t- fl'fl?fV!
2. 3f1R fi7Wfl':lJ<TI woft Vfl fPGi# t dt ~ ;!t
-'1t~truf
3. .-t 1lfimfi61?1'1'11iM-it'l'lf< 'ltki't
4. 41<zlt&<Mn w vl'kful
59. 11Ft fit; w x.2:0~ x1~0~Jfx1+~C:3 'I
x1+2x2 4:4WT wrMR q;«7 ~ 1 ffl f.rq ii W
'""' '"' 'Fffl t ?
]. sx. +1:<, 7fi1 r]l?li{(('f 'if'J 21 i 'q S'fflliT
wt Wlfilo "l'**'1 'lt.r t 1
2. Sx1+7x2 WT ~ 7J!!l1 17 t <1 :::mw.<lfrt
- """""' 'lfl t I
3. sx,+7x, '"'""""' <"1213 11 ::Jfl11f/
"l'**'1 '!!"' 17 t I
4. Sx1+7x~ tm., W <itt r;fffTm ~ ~ 1 ;h
/Wlrof I
S/07 RD/U-4A~2A
17
I. d1:Crease.sas.romovts.away from X.
2 increa.ses as.t0 moves aw:t>' from Jf.
3. increases ~s X6 mo·es closer to0.
4. dt.ocrc.t~Ses a<; :como'cs closer to 0.
57.. A box contains N tickets which are 1Jilbered l.
2..... N. Tit<: value ofN is howt'tr, unknown. A
~impl~ r.mdom .sampl~ of n tic.kels is drawn
without replacement from the box. Let X,,
X?,...,Xnbe numbers on the tickets ob1ain.cd in the
lu, 2"1
, .... 1)1
~ draws rcspcctiv¢1y. Vhich of the
folloving:is an unbiased estimatorofN?
- - I )I. 2X-1 where X = -(X,+... +X..
N
2. 2i+l
3.
- l
2X+-
2
4. - l
2X--
2
58. (n a clinical trial 11 randomly chosen persons were
enrolled to elCamine whether two dilfcrcnt skin
creams, A and B, have different effects on the
h~mllln body. Cream A :as :lpplied to onC' of the
ro.ndomly chosen anus ot' each person, crc.:un nto
the other anu. Whichstatistical ttst is 10 be used to
examine the-diff<:r<.·nce? Assume th:u the response
measured is a conti.nuous •ari3b1e.
1. 1o:o·sample: t-test if nonnality can be assumed.
2. Paired t--test if nom1ality can b<: assumed.
3. 'l.~o·o·samplc Kolmosor~w-Sminl<W test.
4. Test for randomness.
59. Suppose that the ':!riablcs x,1~ 0 and x1~ 0 S3tisfy
t11c constraints x,+xl ~ 3 :llld x1+2x1 ~ 4. Which of
the followi•.lg is true?
1. The maximumvalue of 5x1 + 7x~ is 21and it
does not hrwe ;·my fmite-minlmum.
2. The ntininnun "'aloe of5x1+7x2 is 17 ald it docs
not ha•c any finite maximum.
3. The maximum value ofSx,+7x1 is 2l Md its
minimum vs.lue is 17.
4. Sx1+7x1 neither has a fmi1e maxinmrn nor a
fini1eminimum.

18. 60. 3M"''fl rdrl ).> 0 t1 #in rrfir Jl > 0 Ui %
W Mil ""'f<INrW ~'!Pl. ill; X(t) lffl'i61 1!11
~l'm if I 'll!fmr X(t) ~
L Wtl ' --JL ;;;, c;;rffl. yfj};w t I
2. wfi! 'lfl1 i--~· iii11J<r """' ofib711 g 1
3. ~ r;ffl I. 7.i rrrc7 :rliT~ ;tt vr-r-;•.~
)lfft;rlf !. I
4. WA Tfft! ~a' 't({flf :rfrr .!;fit VFF!- 71ffl
,_ ~
ilfilnlo' !. 1
18
60. let X(() be thenumber of~ustomcrs inan1(/Mil
queuing sys1cm with arrivnl mlc /. >0 and
service(ate J.' ::. 0. TIe pro~ss X(t) isa
I. Polsson proce.ss with rate i...~t.
2. purebirth processWitll birUl rate A-~t.
3. birth and death p-roccs$ with birth r~l¢ ), Md
de:ub l'3tc ll·
4. birl.h anddc:!th JUQC.CS$ with birth rate ~<Uld
death rate .!.
~·
,,
S/07 RD/12--4AH--28

19. 19
( 'Wtl'ort C J
~ 1/Unit I
61. 'lrn'1ftx) • co$(1x- 51) + ''" (lx - 31) •lx+ 10; - Oxl +4)1
"' fm? l!fi!St~ 1 rf.rr.t ~'II
'111~1 31QiPR·fW ':fi1 t ?
3. .<~-to 4. x • O
61. Ccnsidt:r1llefunction
ftx> =C<n(lr- St)+sin(..-- 3D+lr+ 1011
- (IQ - 4)'.
A1 which ofthe followiJ~ poinb is r.ruudiiTeren1iablc?
I. X- 5 3. x - - 10 4. :t ... 0
I. ((z.y) :lrJ S I. bi~ 21
). ((z.y):.1+3ysS)
2. ((z.y) :IriS 1.1)' S 2)
~. {(Z.)') :z's/-S)
62. Which ofthe following subst1s orR'arecompoc1?
I. {(<.y) :~•1 ~I, b•l> 2)
3. {(>.y):x'+ Jy'ss)
2. {(.T.yJ :Ixl s J,b·l'~2)
4. {(.T.y) :x'~~ + Sl
I. d;{.g)= sup{l/(x)-g(z)l :xe(O.IJ}.
2. d;f. g)= inf{( f(x)-g(.t) :xe (O,IJ}.
I
3. dci.g)- flr<-•> -g(.<lld•.
0
'
4. a(t;g)= sup{ H•J •s~•)l : xo(0.1]}+ jlf(x)•g(.<)ldx .
•

20. 20
1,3 ~oichofthcfollowmgare metricson C=({:[0. lJ -> R isa continuous function}
•·'1/.J<)• <opllf(.<)- sc(x)l :.e!O,I]i.
2 •11/.ZJ• infllf(x)- g(x)l:xe!O,I]i.
I
oNf f)~ ff(x) • g(.<~ott.
• '.: o!lfg) $tol>! lf(x) · g,•)l : x <:[O,l]l+ Jlf(x)·g(x)ld.< ·
'
•1. UAJ ~-~~ Tfl1'Pfm 1f1im1 ; I
·-·
~ "
2. unAJ':OI'7'0J"/)1J g I
n'd 1~l
6-t. I'OC'cXhJ• I. 2, 3..... ktA, be* fuU:c .seccon~aan~na atlca.u 1W0d1shnttdoe~es. 1"'hm
'
l . UA1
h a ctXXttab&e ut.
' '•
~. nA, IS,JilCOU013blc.
' '
( I)"''1. I •·., - )L·v·run·-?Q'),
"·
' )"'.l. lll; - >ciJP.l n - '>«> .
65. 'htdl nt the followmg 1s/;m::<:omx:f?
I. (~rI+; ->e b n - ) tO.
3.
,
(I+-.;..J' -teas r.-t-(1().
••
z. UTI...,'"""""'nable.~ljd
•
4. . U A1is unco-m~o .
2.
4.
2.
••
•••
(t+...L)"-;c Qfll 11- >«: .
n + l
( ••_!_r-...~" ~~~<1).n+l
(•·;;rJ'-uasn~co.

21. 21
l. Jog~s10
fX+losr l'l>llx,y>OIItr.nt 1
2 2
2.
!!l e" -t~
e 2 S l ,.h,y>O VI~ 1
3. . ~s•inx+siny l'lt/t >O ot ltRsm
2 2
x.y ~ · 1
4. (x;;fsmax{l./j!Nix,y>OnH~ 1¥/tR 1
lllhicb oflhefollowin&..,... '""'?
l~x•ysloax+logy fo<tllxy>O.
"b 2 2 .I.
2.
J.
••
!!1. e' +c"
e 1 s
2
forall.r,y>O.
. .X+ y Ssinx+siny fi II O
stn2 ~ ora x,y> .
(•;;J'Smox{x'.y'j forollx.y>Oundallk >1.
67. f : Ia, bI -+ R !l'lf >l1l 'lllf'l t lfll'fllll-1'11111 !Wr
d
I. w>fl as c<d S b '*/$Tv- J!(x)dlt• O ~~ [ 5 0? 1
'
2. w>fla ScS b •~f<f~•m ft(x)dx=O m[=Ot 1
• d
3. w»a sa<d s b '*f<f~ "'"'" jJ(x)d.r=0 m'11'""'"""' '1tf t fil;[= o it 1
'
'4. ""'11 ScSb Ill tm!- jJ(x)dx=O lf) zr~ Jlr.mru; '1tf t fil;[= 0 ill
•
67. Let}': (a. b)_,. Rb( aniiC-;lSUnlblc ru,lction. TI1en
d
I. If Jf(x)d.tc O for•lla,c<d,bch<nj•Oo.e.
'
'2. If JJ(.<)dx•O ro..Jio s cs b.lhenf• oa.•.
•

22. 22
•3. If /f(x)dx =0 for 311 a ~c <d ~ b, doe-s not neecwnly imply l)~l f-= 0 4.¢-
'
'
rr J!(>)d.t:Oro.ana scsb doesDO< r.«<ss;;lly implythat/~o....
•
1. <~.-r;fttn;, n.~'ifi t , 2. do·'{frlr if 8, /itrpr ~ I
3. d:·fftrn if BoRyir 'lit t I 4. d:·'ffr" Ifn,flvrr ~1!1 t 1
6S. fotX. (XJ. X:,•..•x,.) andy= (yJ, )':'>····'·~)Ul ~·le1 d,cx.y>·(tlxi-Y,r)flpto; I 'Sp < «>,
,.,
andd.tr.y) • mu 11-rJ~ :j• I.2.....-j.
1.<1 B, • {xoR":clo(;c.0) <II. I Sp <:m.
W'hteh orlbe followitlg are cocretl?
1. 81 IS open m thed,..-metric.
J. 81 1< not open in lhe d:·metric.
I. (0, 0) ""fordmr 8 1
2. 81 isOptl'l Ul the d.._·metric.
4 , 81 IS not open in the d',-mctric.
2, (0, 0) «/ - t <1 (0,0) W <r.ft o'l:<i;-Jr.11111<W oRJlf1<rrrl # I
3. (0, 0) "'f "''"''fr.flo ? '"'!!Jlif',.'fl'il Df(O, 0) '!/""-.,'<!)" <r!h/.
4. (0. 0) 'R1-*qt ""']~ Dj(O, 0) •]riiWII>J t
I. [isd-uous at (0.0).
2. /•1continuous at (0. 0)andaJI dittc:rion31 dmntiUcxW at (0.0).
3 f" dofT<te,.;able 21(0, 0)bu< the ~<riVllt;~ D/(0, 0)is1121 uwc•Jble .
4, fu (h(fctet~ciablc l'll (0. 0) and the de:i'<1tive Dj{O,0) as invertible.

23. 23
I. 11/11®:=sup{!l(.<)l:xe[O, ! ]}.
I
2. 11/lh:= ~f(x)idx .
0
3 11/11~· := 11/llo>+Jl{lll +11{0)1.
I
4. llfllz= fl/(<>fd- .
0
70. i1le Sp3.-te qo, I] ofcontinuous functions on [0.. lj is completewith respect to the norm
I.
2.
3.
4.
11/11. :=supJV(x)J :x e JO, lJJ.
1
ll.(lh = flJ(x)id.<.
0
11111~· := 11/1.+ V(l)l + VlO)I·
urn,· J~f(.•>I'<l• .
71. •r-'1 fil; o....,(r) ={(x. y} : ~'-a)'+()'- b)'< r) 1 R ~) f.lq ~~ <~ <fi/W W~
~/1'
l. D(Ohl(l) U{(I,0)) U Da.Ql(I)
3. D(o.oJ(l) u {(l,O)} V D&2~1)
71. lei D~) (r) = {(x, y):(x - a}2
+(y - b)1
< r}. "Which of the following subsets of R are
connected?
I. D(om(l) U{(l, 0)} U D.,,,,(J)
3. D(o,O)(I) u {(1,0)} u D(o.»(l)
l. X~# (["(if]~ 7ft~ I
3. X~ <17Im ~ I
2. D(Mj(l) U O(>.OJ(I)
4. D<o.oJ(I) U D<•'1(1}

24. 24
72. LC't X • {x• {0.1): x J.l/ n,n e: N} be g~xcn ches:u~x.e topolo8)'. Then
I Xos coor.ccledbut no1 ~ 2. X isntlllltf 001q>0« not c:onoecud
). X 11 ~~.and conr..«tcd. 4. X 1s~·but noccomectcd-
73. P,.., ~· If " ll'J1:r es;•J~lli-f:rfii1ct t ?
I.
[~ ~] 2.
[~ ~]
3.
[~I ~I] 4.
[~ ~]
73. Which ofi)IC follow1ng m~utccs are positive dcfini1e'!
I .
.l.
l.
•• [
0 .-
4 0J
H. 1fi'q fir.J:.!C·nll ~natJr.') ~ ~ Y :SA~ '?J:im ff&w (fiQI"ffRV ~ I ~~ arw'fk Yo
C: ~~A W .Jid4d V ~ JIG!,~ t I 'lr-T fi'li k ~ t:Nt (V11) < 11 1{11 'lf·Y ,"ii, f~:!J ;..c.R ,;; fir:~
A: • A,..t I tl~
7~.
I. ..t. 1.
2. ln>~M A "ll,j'
J. ;.. A ;m qm 11r:f J1"f)!;:rn.rfi:;n 1'ff.1 t 1
4, ~~w J'f{lU Olfffllt~ V1c ,; ~ ~ ::fi~ ,rF-Y1 $ f!rn A.r • 0
I tl A be a nOII•?'(n.> Jint.'lr lrtmsformalion on a tl'ill ~clot' ~pace V of dmtclmon "· L<t th:;
>llb>IXI"'~ 11
., c. Vbe the image of V und::-r A. L~·1 k =dnn Jl111 <, :md suppose (hl1 for some
A.c:t..r: )A. The-n
I. ;. • I
) _ dttA•i.~
l ; iJ the ool) t~g,tnvalucofA.
.: lhcn: rt a nontn,"taJ ~< Ytc Y web thea...t.r =0 for 1l1xc V,.
'

25. 25
75. 'TFf filr C '1'5 n x n Ql<lf~<i $ITUf!' f. I 'fA /ilf W, {I, C, C..... C"') iJ1<1 fil"ln '1'1' ~
wr/1<: t 1 ~ Wit?<: w lh? /irt;r t •
I . 2n 2. lllfir.1; Wlllfir.1; II
4. ;,f.;;;; :#&ftr.p 2.n
75. Let cbe all )( ll ((."31 matrix. Let Vi' be the vec«>rSJX'Cespa.nnedby {1. c. <::•..., ct.}. The
di.me.lsionofthevectorspace Wis
I. 2n
3. ,,:
1. v,nv,.
3. v, + v, = {x+ y: xoV,,yoV,).
2. at most11
4. at most 2n
2. v,uv,.
4. V1 IV, = (x< V, and y~ V,).
76. let v••Y2 be subspacesofa vectorspaceY. Whichof the following is oe«ssarilyasubsf)3ceofY?
1. v,nv,.
77. •!Rfilr N '1'1' 3 x 3 ~"""!if~_, 'J"l t N' =0. f'rr.r ii 'It i1lf'f m/'lt WI ~/t >
I. N '1'5 fi/;nof-J!tU!1 Wf1'ffiCI 'It/ t. 1
2. N '1'1' fimr,f-J!fU{1 il 'l1'ffi'l t I
3. N'51'1'/i ~~~~~~I
4. N >/;liP. ~ """'~erf'r;n l~ '$ 1
77. Let N be~ nonzero 3 x 3 matrix with the property N-l • 0. Which of the foUowing isl~re true?
1. N i~ not similar to a diagona.l m;HriX,
2. N is similar to a diagonal matrix.
3. N h3s Olle 10n~uro eigenve(tor.
4. N has. thn.-c linC:.'3rl)' indCpt.'Tldj,."flt eigenvectors.
78. 'TF¥ fili x,yGC" 1/(x,y)=Sup(l•"'x+e''}t :&,q>E Rj '17 fim7 1 f'rr.r if 'It >ir.J-171/W
•••
I. f(x. y) "!xi'+IIY~ 4 2l(x.yl
3. f(x,y) =HI' +IIYI' • 2i(x,y}l
2. f <x. y) =l~<f +IYII' +2Re(x,y).
4. f(x,y) >jjxjj' +!>il' +2!(x,y}l-

26. 26
18. IC'I ~.)~c:'. C"onOO.cr /(.t.y)=Sup~c·1t·"-~>i: :O.tp• ~}. V."'nthorthc roJJowwg
•••
I. /(.T,)') ,;14'+Jyr +2,(x.yl
3. /(.r.y) =11.<1'+I)JI' ~ 1i{x.y~.
2. f(x,y)~l-<f' •(y 1
+2Rc(x.y) .
• . f(x. y) >ll·rl'•l>fl'+2;{x.rX·
l(<1iiff .11/Uni1 II
79. !iP'f If II oit-•-ril <fj«>• C(O. I) if mP< /J >(<rnr4o'·'ll•l4> fiiF;•ai~T/11 rt ~ <(0. I) '1<
.,...,r:l1J ~ - """"vi) o'lft:)
{f<C'[O, 1) :f<., ·~w 5} 2. (f6CIO. I] :jlO) • o:
I
4. U'c(10, I] : JJ(x)<l<~5l
•
19. Vhd ofdN:: fotlowing.seu attdeose inqo. II (ahe $f>Ue o(r'('at ,...~continuous
(w><I>Onl on (0, I) wnb resp«<10"'P'"""" oopology)•
I. {/<C(O.I]:fi•apolynomial) 2. l{cC(O.li:JIO)•O)
l. (feqo. I) :;<W)~ O}
I
4. if•C(O. I) : fJCx)<lx=S)
0
80. 1flil illrf'. •C.-. c.,Hrt l«iif(.!.)=-"-i61 71'11'1R llmll ~311 '!Ill •M•trf11f<R 'ffl'l 8 iRIO
n 2n +l
rrrt:rmrm< d '
I. J{O) • ill
3. }{2). J/4
2. 2""-2 "N/01 ~r,; ~~ g I
4. ~)m q,)J l1'"tt1FJ!vr fPrR ~~<WI t 1
80. Let/: C-• C bea mtromorphic function 11UI)'t1C 910 sattsf)'ing 1(.!.)=~for "2: 1.
n 2n.a.l
Then
I. ./{0) . 112
l. 1{2). 114
l. f huaStmpk pole at z = -2
4. nosuch mt'r0f1'1(.)rphic f~etioc~ t::Usu

27. 27
I. f 11>1 IIT'Rifil;n '11'1 ff</1 ~ I 2. [fMt I
3. fcO. 4. f' 'IF ~ fi>Rf0 t I
81. LC1 f be on enlire function. lflm/ ~10, ihen
I. Ro/ i.s conS1ant 2. I isconst:~nt
3. f•O 4. f ' is a nonzero constant
82. '<P'f fWf : D-+ El [(0)=0 • /(112)•00: "'"'.M.,.1(• t. ;n!' D= (:: 1:1 <I}. f'lq .j' >I
""" " "'" '1<tl t ?
1. If' (112)1;;413 2. 1/' (0)1 S I
3. If' (112)1;;4/3 and 1/' (0)1 s I 4. f(:) • :,:eD
82. I..C1/: ll_. 9be bolomorplla< ' 'ilh /(O) =Oand/(lf2)•0. ,...,. :&= (z:1:1 <I). Wbi<hof
the foUO'NI.ng statements~ eo""'?
I. 1/' (112)1,;;413 2. 1/' (0)1£ I
3. 1/' (112~ s 4/3 andIf' (0)1$ I 4. f(:) • r, zeI)
83. z e ••lyfN,. zeCai/IIV~"" '
I.
2.
3.
4.
lll"• (z.,C:y>O},
iii'• {:eC:y<O},
L.. • {zt:C:x>O},
L'• (:eC:x<O}.
f(:)=2z+l
5z+3
[-J' l1h!1 ;t .,;w • [~' 01) If'rm< rtlirr.d'!rif 1JlWI1 f. I
ff fhi lt I'd UiW 11 H"~ H'"1$ iR'tR Ylitfb~d f1mf1 I I
tr•t L. iJ ww ilK~ L $ a;w lfklA~u n'U i 1
l!'ilt L' il ;;w wH'W L',;; <P17 Rll!lillihl """'t 1

28. H' • (:eC:y>O},
It"• (:oC:y<O}.
L' • (:<C :x>O},
L t:cC:x<O}.
I. mnp~ nr onto M' and!i·r(I!HO [-r.
2. tn<lp.$ 1r OlllO H' nnd )['onto l•C
3. 111;11)$ u· QOlO L' and [-j onto rt.-.
4. m.ap~ Oi' onto G;and HI or.to L'.
84. :•OWII!?n' /(:}=cxr( z ) ""
I-eos=
I. !"" J;v*• M/P.t"T t I
2. ~ Jl"Rf>< t I
3. '4'< JOf.r"Jrli ~ ~ I
28
~. :- o.t MR amj(') d! ~ ;~«R!.,., >l y.v.y,. •"' w-.rw • """'- f1l1f: .,;
Ill
84. At:: • 0. the function /(=)= exp( z ) has
t -<::OSZ
I . 1 •.:ln'.('IV1lhlc sitl!)'UIQnty.
2. :>pol<:.
3. an cllsc:ntial ~ingul:tril)'.
J , !he l.nurent exp:m.~ion ofJtz) ~ound: =0 h:I.S infmttely m:any po:~oitive and negatiV¢
J)QWCf'$ O(Z.
85. 'fl-1 (.), It • Q!x)II om I. I + x'"" ;#;o '1<1 >n<•l /. I .r-1 .Q< R h ;fi/ ""'d'J"f" )' t I
al R Vl ""'~~· t
I.
J
>) 1 l1!1o 1rretlue1ble0'¢1' R.
J. >"'-y + l IS UTeductbk O'er R.
2. •)'"" • y • l
4 l•l·r • •
2. l +y + 1is irredocJbleovtt R.
4, y' + );. '"y+ l i~ u-rcductblc over R.

29. I. Sint'.Q .,.lflof/>1/. 1
3. s;.-••.Q .. -~,
29
2. Co. n/17. Q '17-I 1
4. .Ji~,J;.Q(x)w <ll<i!/r1 t 1
·,
86. Wh1ch ofthefollowing IsLruc'J
I. Sin'fisalgcbr.llcoverQ. 2. Cosit/171SalgtbraicovcrQ.
3. Sin~ I isol~o•.,.,.Q. •. .Ji+.fiIS algebr:ri<O>uCl(• ).
87. m"f f>;j(x) - :?+x1
+.t +l ~·g(x) =.-.'• 1 nltQ[.<]ff
I. '1/'mT>< """ ¥1'1f1< (/{.<),g(x)) =x + I.
2. Jfilm'iJIPP/10(1/f U(x),g(,t))=..' - 1.
3. "'JifR fPIPIIId (/{x), g(x))= x' +...'+ x'+ I.
4. ~ H•Nor# (/{x). g(x)) = x' ~ x' +:J + x' ~ I.
I. g.e.d.(ltx).i(l))•x+ I.
2. s-<.d.(A,t).a(,<))•x'-1.
3. l.e.m. (/{x),8(1)) • x'+x' +x'+ I.
4. l.e.m. (/{x).~o(,<))=x'+x' +?+x'+ I.
I. HcZ(G). 2. H =Z(G).
3. G If H lmT'll"' I 1 4, H <'dlJ/TO#r ~ t 1
88. For 3ny sn>vpG oforder 36 andany subQrOup J/ofG order 4,
I. HcZ(G). 2. H= Z(G).
J. II is nonnalm G. 4 , /lu an abcli•n group.
89. ;,R. ffti G a'F-S, x SJffi1 f¥i!rt: llm1T 1. 1 n)
I. G <m" 2. 11m <l'ffl'f,l! fTf11'<F'J t. I 2. G .. ).l11!1 'IW!'f.l! ;an-t I
). G lli1 "'" "'!J"' 1ffll'll"' """7.1' 4 I 4. a.,~"" """""''J'fO'J.l' llllft n '"'t

30. 30
89. 1.<10 dcn<Kc the groupS. • S,. Then
I. a2-Sylow•ub-ofGis,_,l
J. 0 h>S onontnvb1 nomu1"'bsnr"P·
2. a >.Syk>wsubpipofG1s nomul.
.1. c;has a~l subpoupoio.rdefn.
90 ~ iW X ("fJ' 'l'lfi'I(R Gl.,.&.fith ~ t 1 ~:, fJ; ,,.A:_.1 ,, X • lf'{iit ~~ I "'t ~
""'f'fi i 1It'! X <1'1 I'"' OiJi1 ••aQ'" 'if"ldriJ <6<« f•4tll mfl t m fix)= o, liR x.A,
J•l.l.).
1. ~ (Jim mo m1 t:r.t rn ~ ,
2. 'i/;'ff lt ;cq n,,,,,,al q ~ t/t ;:7 m.;:;:-~ u} N¥R (.)<=l tri II 1
3. t11, tr:.fi1 ~ ~1 iff(fl/4<1; :ffd! ;/; fc:n) I
4. ,.,;1 :'/11 ~ tf,, A~ f[if A) # wf!l1l ~ ~ I
90 LUl Xb~ ~ riOI'Il'llll H~usdorffsp:!.ce. Let Ah Az, A) be: ct~~d subitC$ ofX •hich :HI! Jl3irwisc
<li~JOint. 11lcn there oiW3)'S .:xi~ISs continuous real valued CVIlCiiOn/Oil XSICh th:u
91.
Jiy) u,.it'n.At.i- l.2,3
l ,rfeach 3, l$1!'tthcr 0 or I.
2 .rrQC l~stlwo ofth.;: numbers a 1. ~.a~ are 4.-qu~l.
3. ((lr all re~l wlue~ o(u1 • a~.Q).
J Otliy 1fone amcY.1i; lhc stUAt,A~ and A1 1S empty.
Y [>·,(x)] u)
>',(.r)
Vl5ili UJ.Il:nit Ill
I. y,(x}-+ oo ~Yl(x} - ) 0 w: x-> a>.
2. }'o(<) >0 <iy,(.t) >0 or• x - ><IJ.
J. )'I(,} ><0 '4 )'~(.'} ->-(f) WI X - >- <0,
•1. y o(r). )':(x) ->-oo iirll x -t -<10.
91. (.'QO$Jdc:l the SY"k:mofOOE
.!.r.,r. Y(O). [
2
-J
tl'f -1
"!>= A-(1 2)lnd Y=[y,(.r)]· Then
0 - 1 y,(.<)
I. J',(l')-• 0'>3nd)~(X)-t0 3SX ~~.
2. )'l(')..,.O«~ndn(x)~O~s .~· ~ 'i'J.

31. 31
). rA')-*O')aod):(.~)-+ ru.r-.-«.
•1, y,(x).,l-'t(.Y)-+ ·tiJ as."-> ..u.;,
9Z. 0/t<il>v ""' .,...,. y" + i.y =0; )'(0) = o. y(l) = 0... /1;11 ~"' '-"" ~ ""' " ..
Jlfktm t. ~,_} (0. I ) >Y r;.r. Jil;l~ "''"' ffrnf 8. vii
I.
).
2.
4.
92. l·or the bol.lnd:rry value proble-m
93.
!N.
Y' + l.y • 0; y(O) • O. y(l) • O.
l~ cxisb an cigen~tue Aft>r •"uch tho:rc C'JOrtC!;ponds on Cttcnf'hnction 111 (0, 1) thllt
I . OOc:; 1101ch3tt.ge JtgJ1.
3. is po$AIJ't.
I.
""1"' 2. ~
2. cl:mg<:s sjgn.
4. n negative.
3. ii.IIWA11i 4.
t/
2
>''ThC'solution o(lhe boun<bsy vaNe problem --;-+ y-a:cosecr, "O<x<-
dx· 2
y(O)=O. y(; )=Ois
I. convex 2. conc:we 3. neg:ui'e 4.
I. Wtft x &(!(. YER It Rr1i "• tWIt I
2. ((X, y) Elit' : (X, y) ~ (0, 0)) '1' '-"" """" ~ f. I
3. {(x. y) eR': (x, y) • (0.0)1""1"" ~ r<r t 1
!R(i"qi}l
posiLive
4, {(x, y) el<': (x, y) • (0, 0))'" 'Ill'.,....,ffl 6. W"J 1rR Jl'dm; t I

32. ot(.<.y) =.T,
!....
I. asoluctOn (o( :aU xeR. y•R
32
2. an unoqu• solution ot l(t, y) •~: (x, y) • (0, 0)1
3. abowlded oolut"'n'" !(x. y) eR1
: (x. y) • (0. O)l
4. an unoqucsotuuon m II•. y) tR': (x. >) • (0. 0)}, but theso!u1"'"••unboond..-.1.
u, - uu =O. O<.t<Jf and 1>0}
u(O.r)-u(.T.r)-0, 1>0
u(J.,O) =s.tn.l'<t$1D2-'. OS:xS r.
I. .,ftx£(0, ::).1 r..~ .,(x,r) - • 0 <illt _,"'
2. W'f1xG (0. x)~ f?n) t',.(x, r) -t 0 iffl t -+G>
3. .tc (0. r.). 1>0 Ill IM c'11(t, 1) 'll1! 'litq """' ! 1
4. •eDxe(O, ~)•> Rnl •''u(x.r) ->0 1lfil 1 _,. «>
95. Let ., be asoJuHon orlhche;u cq1t:11ion
u, -11"~ =0, O<.x<r. ond t>O}
u(O,I) • ot(/1,1)• 0. 1>0
11(x,O) =$in,'+Sin2x, O~ .t$1:
l. tr{x,J)-+ Oas t -+ oo roc:~ll xe (O, ,or).
2. lu(x, 1) ->0 os 1->"'foroii .<C (0. If).
3. tl•t(x,l) is <1 bounded funellon for :ui (0. JT), t >0.
4. e:J(x.l) _, 0 :a,.;t -+~for all xfi(O, tr).
96. 1iRJr;}; u flftTffrr. IP. wwm
u' + ~~~·• /(1),
I
u'(O)=o, u(l)•b
1e(O.I} }
41

33. A.H
•
33
<61 Tf'l I u! +IS I It~ ~ ,.., ~ >{>, )') • u(Jx'+I)~'>' g(x, y) •
!(Jx'+y').•tv ~-lf'll-
v,..+v,=g {cx,y):x'+/<1)>1}
v(x,y)=O {;T,y):.'+/•I)Q?
I. a>O~ h >O
3. a=O ~ b=O
u•+~u'= f(t), IG (0,1) }
u'(O) =a, u(l)~h
2. a >Oub•O
4. u<Ott b•O
Define for.i +-I ~ l. v(x.}''). u(,Ixz +;)a:td ~'(:c.y) = r(J,t2+l ).Ihen v i$ 3solution
oflhe POE
vu-rvn=8 in {C.t,y):x
2
t /<l}};r
>(x,y) =0 "" {~<.}') :x'+y
1
=I}
I. a>Oandb >O
3. a • Oandb=O
2. (t>Onndh • O
4. a<Oondh • O
91. >tF fro SJif t ~ If" aqR{)>p ~ [UTM) <§••·•·»• l1ofl C ... <mot rr>/1 {.)""" m>PJ
'Ff ,; PFr f. I 1'1'-1 ~f&J; rmTrfl Q?·fi/rn7 I
2x1 t-3r2 -:r) = S
4x1 +4x, -3x, = 3 (I)
-2x1~3x1 -xl: 1
rrl """"'(1)
I, {!l6 U'fM /f ~~ 11!1 WI 1fl1rth ~ rrr-iJ <tC Tl'fii.'f:r-1Jll •fll # 11JJ'if~ iJNi6 t:Wit1f1
Y~ 'Ff il fiR 'f,f/ f I •
2. ~~ ! lJTRifih U'rM ,y 'l'h'rifid aft :raJ :;(; ~ I
S/01 RD/114AK-3A
'

34. 34
>. ~ JM • ~' "'' :17 ~ t miff<>~~"' m ~ ~~·r fJ"" <1 .'~=? r,,
~. l'T~tS 4,..ClJ-aRi1<#17ll~#{Til'l~{ <1>7r.<"(t) ~7tf)(Rff. I
97. (jt~1 du1 an upper tnanguLY rr.atrix (l;~ is ilt"Miblt tf and onty rfalllC$ di:atontl
clcrn.:t~'.lo ~ drff~n:nt from.t~ro. eo::sider th¢ I1~CM t.)"(te!":"
I.
'-·
2t,+.h;-.lj -5
h.•4tr- 3x.; ~3
2..t1 • hz x~ ;.; J
(I)
(,ln be hllbiOifl'ICd 1nt~ an UT~I hut is not rnvcmhlc l'!ccau&e the diagonal
~:tur•..:s uftl•c UTM one n(ll ,Jjff(:tC!ll fH)Ill ?.CtO.
h uwcrublc ~hough ':mno: b:: tr:wsfonucd in1o an U'l~l.
3. CJn be trunstOnmoJ tulo au UT~f becau~e above du•uon:ll c.nhJ.::s :.u~ all dtiY'cr<.'m from
{1,!11),
can be truus.fonned intoM UT~I ~od lhe solutionof;he UTM 1~ tile wtution or(l ).
2.
.1
J
~(.f)
Y.(.t)-
2
2. g!.•)-(.-
.T
It) .l• l -2 '"' 0 (1)
I ~·t Y J.,o( l. su ll•..tt all) !i~t>d ;wintof:.,'(.'} is a ::.l'1utiou -.>((I). 1'111..'11
,
i,'( ")
)
t( 't• "": 2. g( -r)""-i .._ ..=. :'t"~JXlo.<;<ih!ce~
T
X! -:r-:!
~C)•t- - .A. ;0. KcR :s3•VK..•bli!!<hOtC.:
K ~-
-'( ) -- '~ - 2. J:l-') -I- .=. <lit' lht' (,.'lily po~tbl.; ~111.11"1,!)
,(
I '
S/07R0/12-4AH-3B

35. '
~>9. """"""wl/1lmr ji(Ji)=.t fK~<,()9(()d(
0
<il!!f2 .,.. .,... II.
r:0 K(;r,()={cosxsin(, ror OSx<(
cos(smx, ror ( i!.xSn
35
t. 'l'l' '1fMt'l1 'IR i'PmiT #'(x)-}{.1.) ¢(x)=0, p(K)=0, /(0)• 0 1111""' ff 011<11 t
<iriff.!{-<) - I 1111" 'lftlJJ>o ""' - ""
I. VWj{A) • 0, 'M JJ"<PW CCI I I
3. ""'j().) <0. lOii ffl ;;if I
99. 1'he integral equ:a1ion
'
p(x)=). fK(x,()o>(.;')d(
•
2. ORJ{J.) > 0. 31''" f#!zli <il ffl t I
4• "" ).> I, 'l'l' .,.,., r<l t I
{
COSX$iR,, forO~x<(
where A: i~ a J);;nunetcr, snd K(x,()= ·
cos,slru, for( S.t·~;r
lc>ds 10 a bounobry v•lue problem jl'(x)- j{.l) t'(x) = 0, 9(•)" 0. ~(0)= 0. wh<:r< ftl) ;.
....,.,. Then ohe boundary,...ue pmblcm hu
I. 'uniqueso!tllion whenj(J.) • 0. 2. infinite numberorsolutions wh<.>n ;t;.) > 0.
3. no solution 1/henj{).) < 0. 4, aunique sohnion when l > I.
100. lftf(f.llll l(z(x.y)) • [{ (:)'•(~J-2z }t.rdy em0 ~"" t/NI' f.. ~qf11fl•lf w-I
~ x ~ 1.- !~ y ~ l, fl z • o I It Df.Pi:Ft$N _, Mm lSI uf"'~ eaz• i:O(''f,y) p.
...~~
N
I. z0 =I,a1~,(x. y)• 01111a,~ f. 'IfD w '"""' ;. r::•rnrm: ""*t I! 1
•=I
2. z.= a,;,(x,y)+a.-9.{x,)•),;;nofa, <F1 a,~~ <F1;. • Q1 .t """'~
~rJtlf.1
J. zo = a(.{x. y)oma fl<""" t r:OD "'~ ''"" f. 1
4. :o=(x2- J)(y'-1)116.

36. 36
I00. An app:Cl'lultat-: S<ll'•liOn 1 • 1., (x. :;) 10 lhc problcn1 ofexrremi:cing «he fuJ)cti<ln.'ll
/(:(.<.y))- rl(~)'•ll~)'-?: ldui;,
•' l <> i)y
t.~.·rc r> 1:. ~l..: ~~uJ:~. I sJl. ~ 1.- 1:< ys l. ~~11. • 0 on the bou.nd:uy ofdlcsquare, isof the
:Om1
"I. =•- La,(. (x.y). "f.ctc a. arc cortIMlS and fuoc••ons ~ 3tc ll!te3tly tndepcOOI!'tlt
'•.
'
'
Ill I>.
~ ~ o 6-(l,)') ..a4'(1C. J'). v.hcr.: a »''d U11JC ttlft!iU.'lb. and~ md ~love
wntJnuoo:;. putt.~;) tk•m~~~~
:. '= ad(t. ) ') "btrc at' 3 C(IRCUru :tnol6 ·~ CO.'ttlnoou5 1n 0
:.-<.t1
- iH,:-IJ'I(t.
l .~...~-( Allrt ~~Nft flcKI ::tl ~ 'r t
l ..•: •M .:..'lll~.Jr' r.t..'llWi $ 3.~ ~ m $ 1Wr1 1tm :rtf ilTiil. 1ffitie-t RtP1
-"~~J; ;~ wft:r4 ~ :rrtt mr ,
,, ,!f.'tr<·r }',):Jtt {'(fll .f't <t1·1~ol·'lfl ff1 Jr.)~~ .t t
••• --lC-1 .,.r .f,rfM f-1'711 ~JrR!'f r-t:<JJ~ 1Ft J,'J'T1'fl t 1
! I l:ml:iton'srrlndplc rollon ~; ((('Ill th(' J)'AlembCil'~ llflnciplc.
2. Ihutnllvn's prua·tplc 1 IXJ1 munlly <~i>l)lic~blc to nonho!onom•c system. unless a
relation oo•utcchut! 1h~ ~hllC•·etUI:It ofgau:mh"-'C'd cooulirutlCl is gt·en.
3. Jla•mlhm'1- p•·i~l!tpl...- th llow.. rrn1u 1 .11gr.m~..::'s ~qu:llflW~.
<1 r-.~wl..,tt's Sl.!l.'lttd l.twuf mulion folluw11 fiutn ~1c ll<~ruilton's pritt<:ipl~.
I. t•FU~-.~ ff4'o!•+<''lf'it•fl<l J,},. II~ ,lfil·fi~'l ?Jift;"J;fv} f. I
2. v;•/}-MVJ) f/~ tJ,·r NO:.<lJJ •••:HINfi~Jtcl {:)Jfift~~Y tJiJ (({.PJ/ tJ} ~t;IN if I
J_ f(!,';,j{ l,Jo"'~ fl,,'>/f:l•h ¥01:,' ~ J{lfNI •lf.l ~. ~r>f•!( lifllr.At IJfit W4ttr--(t-it m'fl'r; 'PI
'IR,.-..'f'Jf ~m it :
4 ~•ri/ ?mi•NI .Jl1P.'frl (~ t.•flfr;.fl IJJcN 'a/{ff-:}~~·cl '11/(t 'ifil ('ifi /i:tmtPI f:iifFf it I
I.
'
3.
L:o~~J.a••s~':s ('IUJ.Iton" an: sct:onJotdcr 'hift:n:nti:al t.-qUJtion.~
Toul number ot ~'!u.u.vol) ~ ~Ql:Jl kJ the ''~•mbec of'l}!rlet:lliud
~oo."la3.e$,
LO~inl::•:a.• l c. nol un:qut: in ll'i funtuon:JIIorm. buc the (onn of dtc
Y~llif¢C's cqolCIOnol· mottOn ~ bt~s~n'<'d
l..al,Tiltlg!Oin flll':c-IKMl 1::I q11~lr:mc fun~(!Ot'l n( ~rDh7ed -"Ciocil)' When lhc
j'Ol.('nlt.)lle'US~<i.

37. 37
i"PQf I Unit IV
103. 'll'ft:IY F(x, y), G(x) ~d H(y) ifi'M (X, Y)1117 ory-«r- m ""'"- X"'1 oW1r riWI ~
'"R't <f.1 Y <Pl '3'l17f - """ !,6«< f. I qft>nftH ~ flly
{
I ~ xsau-
- 1 'IR X>n " •{ I- I
I. ,.. ,.."'"' (U, V)= 0 Ill fi'll x • y <$ f<t~ f (x, y) • G(x) H(y)
2. N•r«r41 x • y ol ~ F(x, y) = G(x) H(y) nt ....,.,l'>l (U,V) = 0
3. oWl? U .. V oml!t ' •) X • Yw.nt d I
<1'. JI1R X <1 Y r.rrif:l #'fl) U :r V ~~ntr ! 1
103. lei F(x, y), G(x) and H(y) be lhc join< e.d.f. of (X, Y~ marsinal c.d.f. of X and
m~r&in<~l c.d.f. ofY respectively.
Define
. { ' if X So
U =
- 1 if X>a
and ~'•{ '- I
wherea and bareftxed real numbers. Then
if Y Sb
if Y>b
I. IfCov(U, V) • 0then F(x, y) = G(x) H(y) for 311 x andy.
2. lfF(x, y) • G(x)ll(y) for all x andy lhen Cov(U,V) • 0.
3. lfU and V aJe independent then X andYsrc independent
4. If X andY are independent then 0 and V ate independcnL
104. f.lnr Jf 'II .,,., 'II ;;iit;r11 >Jrf[/qq; ..., X~ Y oil "'"""'ollo;)r 'liim .,.,; t ?
I. ?l>l)ae R ol RrQ P(X> •I Y>a) • P (X >a)
l . ria,b e R ol Rl>! P(X>ai Y < b) = I'(X >a)
3. X~Y~>rl/81
•
4, ffllo,b GRIG~ E[(X - a)(Y - b))=E(X -a) E(Y - b)
104. Which.ofthe following conditions imply indepcnden<;e-oftht random variables Xand
Y?
I. p(X> a 1Y> a) • P (X> a) foralla e R.
2. p(X >a 1Y <b)• P (X> a) foroll n, b G R.

38. 3. Xand Yare-uncotrelated.
4. E!(X - a)(Y - b!] = ~(X- a) G(Y - b) for all a, b G R.
lOS. :J/'iTP..1 ?'Pd~ s=~ t;2,3.4,5} ~ ~ w~1 t;F/Vi!ifft P viT ;ft't! ,7p;r 1'f'1i'! ff. <JR9 f'N ;r,<mu
11~<11 w R~•rl
rO~I 0 0.2 0.1 0
0 0 0
P=l0.7
0 0.1 0.2 0
0.2 0 0.7 0.1 0
0 o.s 0 0 0.5
I.
10~. ('ons!dcr :t Markov chsin with St:Jic spsc-c S-= {l ,2,3 ,4,5} and stalionary tnlrL~ition probability
m~trix (• gtwn by
' 0 I 0 0.2 0.7 0
0 I 0 0 0
I'= 0.7 0 0.1 0.2 0
0.2 0 0.7 0.1 0
' 0 0.5 0 0 0.5
l.ct p~n) b::th<: {i,J)rh d cmcm(lf/J'"
Th.:n
l.
'
,
L tim p~~~; -t.
1
·1-",.
(0.25. ().25.0.25, 0.25.o; l$:! Sl"liOil:lt)'dis.ttibutioo for Ole MatkO' ch~il,

39. 106.
106.
39
}. f Pt.><«>.....
4. lim pf:)=J/3.
-~~
(i)
(ii)
(iii)
~;.[;x E R ~,., fi."l)d? u fi nrttu(-x)- -u(x)
.u (-1. I) <I Ri'~ 11(x)=0
I
m11H :R <1 f<'l';; ~~·~s JiJf
2 "
1. /:tlliflf'lih "fr1 ~ ~ # I
2. 1"./1X ,; /iiPJ/(.t) > 0 '1/j ~if I
3. R '{'{f '{'!' ;nfiJ;mrT "''"' ....,. f. I
I ..!.,,~
let R(.t)=-z.--e l forx • Rand u beil continuous func-tion on R su<h that
'o/2:<
(i) 1>(-x)=-o(x~ ro...IJX • R,"""u ...,_,.,
M u{%) =0 f« xe (- 1. 1).
(ou) Jii(.T)fs -;/ •rorallx< R.
2 2tl'e
l..ctj(x} =&'(.') + tt(x}. for all X 4 R. then
I. f :;l.t take nct;alivc v;;alucs.
2. /(:r) > (l for ;dl.tand[ i!; Ml integrable.
3. f is a p.rob~bility dc:1~U)' ful'lc:tion on R.
4 , I is an intcg,robk f111KC10n
107. ""'fit; X, X,, ... """'urf(I>F#; w I. <l1<fX.. -n l1 3n (n =1, 2....) <i -<t-<r ~ '""""''""
~t I 'Uif F.; N = I, 2. ... r6 flr6 SN = );, ±:!,_f'1'S, <liT •1:'1 ,_ P, If I 7PJt ••-1
vN ...d n
~ Cf>~ :rFP$ 'iUTI1fRI 411fib:c:r, fr? ¢ i'lt;.r rtiFPf itfJ f.)f{r(J 11m11 t I f.rq t) ~} (Jft.l...m/tf
111.1 t/l >

40. 40
lim f:V(O)S<I>(Ql..._. 2. lim ,.::.,(0)~<1>(0)
.'....<6
l. Inn r:,.(I)S<I>(I)
·"'-"'
107. l... X,, x,, .. be: tndcprndcnl r.lOdom variabiC$ With x.b«<&umlomlly <ltstnbutcd beWeen
n o.nd3n.n= l,2,.
lOR.
'Lee S ~~t X" ror:-; -= 1, 2•... .md let 1:~ be the distrlb,,tion function ofS~. Also I~ <1>
vN ...1 "
denote the di.stnbudon function of a St<Uldard 1sorm3t r1ndom vamble. Whicl) of (he
f(lllowinglslart lmc-?
I.
).
2. lim F,(O)~<l>(O)
~-'-"" .
4. lim Fy(l) ~ <l>(l)
o'-."'1 '
2. x,• 2x,o.t ~ w4<1 *,
I
-(X,·2X,),Or#~'JM'f.r~<rt I
2
IOR. Sup1xw:c X1h:a$ density J;(x)=~e-...:o,x>Oand X: h:.ls density fz(x)•~((ltnl,x>O and
X., X,:.re ind~.":~ndcnl. Th¢n
'••
4.
x. t 2X: Issotncicnl tOr e.
1
-(X,~ 2X2)i~ t.mbh•~d for 0.
2
J09. '111 .9t t:'li~ .,.,e.n ( ~ 2 H*~>??"iH'd': ~ fW W1ife7f ~X~. Xr.....X. #. t:t i(<P. ~ .s;;;:r
~~... <J') m '*""' ~ _,< p <ov{'O' O<o' <oo n.t"""", I ot
1
2
),
4
0: ~1 ,J.~ l().~ ~<f lR 3Ffiir-ro ~I I
o: _, .,..,,.,;;a ~ ;;(Rq ~l:ia ~ ~ o1 It~ r;.~ .JtW'iiP. 1Jft
~ it llf11 ir-1 1J<Cq ~ tRb f I
o· It .~ rr.if.tm 3Gl1i8"1 fll 'f'.st'1IJ'ffl' "l'f.."1 rmm ~ lit* """*'wm
·"'~~~
Ol ~ f0fi'J ~ ~-!.6l·o'd -3-~ tfi ~ ~ •7' '(,'lft {fm Jl~ $(It~ ;pf I{1VII ~
iJ,,, /, I
'

41. 41
109. SuppOSe that we ha.. n ( ~ 2) I.Ld. observations X,. X,,•••.X.eac:h •·llh a...,.,... N(}J. a')
di$triburion. "~~ < p <co:aod 0 < q
1
<oo s.Te both unknoWIL The-n
I. che maximum likdihood eslimalt ofcf is 311 lnbi~ esrinute forcl.
2. the uniformly minimumvariance unbiastd estim:ue ofa2 has amaller nl(:M squared
error than dtc: nuximum likelihood estimate of~.
3. both the maximum liktlihoodatimate 8Jldthe unifomtly minimurn vnriancc ~timate
ofti are asymptotically consistentes-timates
4. for any unbiased estim:U<! of0:, there is. another estimate o(a1
whh a $-Tmller mean
squ.ued error.
110. ""'~ x, x,.....x,. .v-...m to- l'I.&HI 1>~'""' ,...a.,.,~ 11 ~RroT t. vm-«><o<"'
~ .J!~ Jm1"R I I tit
I. Rfimf '""l 0 ..,~ ;JI;<rR'f t I
2. 1lf<Rd 7fi;rn;l. e•~ w~-~ 1 ,
3. gfimf 'li"l; 0 ltf1 ~il'fl'lr'flr: "J:'11f'f """"~._., 'Ttl t I
4. gf(r<"~f ¥fi){iff1. e(fiT e:¥w•n-l<ov: ~ !fflFJ1 3AfiRrr ~ 7ftf 1 ,
110. Let x1,x~.....x!jbe i.i.d. obscr'li.tions from~ unifotm distribllion on Uc interval (0 - %.e+
!IS ) whcre-oo<0 <co is on unkno1.11 paramt.ter. Then the
1. sample mean isM unbiased estimate fo. 0.
2. ~Je rnedi:.t is anunbiased estim3.te for0.
l. ~ae mean is not che uniformly minimum"-ari3aoembiJ.SCd cswmtefur 0.
4. sunpk mcdizln d not i.htuniformly minimommancc:unb~ tsCWl~ for9.
Ill. ""'f.l;x """""' if(x;I.)•A<""", x >O, ;;ffl 1->0 JIWi'ft 1..-. k <X~ k+l, k ~
0, 1,2, .... ?,X »Hil~~ >I Y=kfil<mrt I Y '*m >IY,. Y,, ..., Y, 'f'l'~
I ' •
1>flmf muiliff t 1 ,-:rfilr l'=-L;r, 1 ni .< w 3ITf["'fitfrurmmw A t:
,;...
l. 2.
. I
A= -= + 1
y
3. 4.
~~--"""'I
111. S'UppoS¢ X h3s domry f (x; ).) • A,e--4, x. > 0, where i. > 0 is Ufl.ktlown. X is d.iscretized lo
gi'e Y""" k if k < X s. k + 1, k • 0, 1, 2. .... A tsndom sample V1, Y.:•..., Y11 is available-
from the dislribmion of v·. Let PI:J!.f,r, ."lben the mcLhod of momc1ll$estimator j of i.
11 t..1
is

42. I.
: }
I'.=-=
y
2.
42
• 1
J..--+1
1'
) .
• ( 1)
;..;;loll +y a. the: so.meos tlte tn3.ximumlik~lihood c~t1n«1tor
112. ?."iff Q.'M;2ili x i /({V Oft~ n#irt, &uf'i[ ((x- 0) = f {0 - X).~ ffifl1 ~ <PWS
~ rrt ~ 714 (~N:w:m. ;:<T:j;i ~ tt ;;m;, t:tM f. X1• x~....•x,. 'rdls-111 lt:9 • oo;:rn
•
u,.:&>o~~~fit$~J:/i'Jqf.., s.~L ~ CXJ.VIif
'"'
{
1, mil »0
f<:3 (.<) = O,llfll x• O w fi#;H 1
- l,<rfil« 0
'iR fi); z..,"fr:lfli ~ •r.r W7 v;v.fl 100(1 - a)=' mRPrr1! I_ ;;;rn0 < Q. < t I nt f:'lr.r if N
""" i11/ i; ;q!) t/f. ,
I. oft 8=0,
"' lim rfs.>.Jn:.}=1
·~ .
2.
'* 0=0, ~~ lim r(s">fn•.}=a.........
) . mil 0>0, u) lim P{S,>,I;;za}=I
Jl • ' "1
•• <Tfil 0>0, ffl limP{S.,.>,r,;="}=a
·-··
112. let X1. ~.....X.. be l.l.d. obsotr,·:l(iO:lSfrorn ad!:Stnb&CIOn with continuous pt~hly dc:nS:it)"
function f whieh is symmrtnc around 0 i.e.
1x-S) =f (0- x) ft,r(IJI real:c.
•
Consider the test J~: 0 • 0 'S H,. : 0 > 0 nnd the: ~ign teststatisticS" =Lsign(Xr) whe;e
,·:.1
fl. if .»0
sign(.<) =10. if x=O. 1..oo z, be the._,100(1- ")lh p=cntikoflbesoancbrdoom,.1
-1, rfx<O
d1$ltibmion where 0 <o. <. 1. Wbich of the t'Ollowing i&'an: ~et?
1. lfO ~o. then llmPis,> fnz,,} ~ L
"''"~ 1
'

43. 43
3. If8>0, then lim r(s.>$.z,J=I.
-~~
113. .,., ~ x..x,....x...N(O,a')."' ~ 10 wf.r>I>'T<IT '"" ~"' •TTfllnr •filffl*I e•> ...9-N(O,
r>. r..20 :n ftrnf , ;;F}. fi';; x=..!..f.X1 ma;~. ~ ;fc:i i5l ~ 8ifO Cff((ff t :
10 (•! •
• - • 20%
I. &=X 2. 8=-
21
3 8,;x if x ~ o 4.
113. Suppc>se X., X:,...Xu> is arandomsample fTom N(9, ol), ¢ =10. Consider fl)C priof tOt(;),
e-N(O, ..'),., =20. Let X=_!... I;x,. Then tlle mode &or o•• posterior distribution for0
JO (•I
satisfies:
I. B=X 2.
, 2oxfi=-
21
3. o~x if x....o 4. 8~X if Xso
114. (X. Y) l1'l fii>U 1fil f.tt:r rff'J yYcff tR ~ : (0, 1), (I, 2), (2, 3),(3, 2), (4, I) 1 ;it
I.
2.
3.
4.
9
X 'T7 Y<6f"'J'f"f- IT'/ '1/Wt; ""''17/Wt Y = - I
s
Y >n X W ~-iPI fflNi WIT<mVT t X a 2
X <r Y •h4t<nsr 'lTffl;iq 'J"1ftR 0 t !
X l.1 Y <i: ;/r.; (1;1 ~ TjVlfrfi + I t I
ll4. Consider the following five observations on (X, Y): (0, 1), (1, 2), (2. 3), (3. 2), (4, 1).
Theo
1. The least-square linearregressionofYon Xis V e ~-
2. The least-square linear regression ofX on Y is X=2.
3. l11e con-elation coefOcient ~tween X and Yis 0.
4. The correlation. coefficient between X andY'is + I.

44. 44
II S. ""' !* .,. t,.... C. ......."" l'fli'9 ?1'1 <hi(O, ct') 6 "'J"" ~ o I Y,. Y,,.•.,Y, $ iiR >f
RdHW~~~rm#
Y, •p+ c1,Y,.,-p=p(Y.- JJ)+,ft-Jl ,,.,. i=l.2....,n - l;
l •
'i!fYf./; T =- L Y;#O<p < l 1fo'>O 1 f17 n~ 2-*~
)/ (- 1
I. T "f'P IlWMPV ;Wf -8 I
}. E(T) ~ ,u, """"(T) > o'in.
2.
••
T fh1 "Y"i1'1J1 r::f r:rmr:1 a'lu ff I
T-N (p, 8') omo1>cr11n.
115. Suppose tto th··· ~ an' u.d. :-..xo; cr'). Qlnsida' v•• y'lo····v.. defined by
r, •p.f. c,. r..:-11 =p(Y,-p) •Ht,•., 1=1. 2• ....n-1.
Let T=.!.:t>;. SuppO<e0 <p < l ondo'>0. Tit<n for"~2
It i:l
l.
}.
'l' has a nonm:l dislnlluliOtl.
E(T) =p, ,,..r("f')>a:tn.
2.
4.
T hils m~an J1 nnd V':'ltiancc fJt/n.
T-N (Jl. &2
) where S::;. ~/n.
116. ~.. ~- if ([/$ ~.. q,; 1# flrrf """" alii 'Ia! iii) "'3""' p 111 Jl'""" ii!J Rn1 '1'1 '-"';
ff.!Hrt ~ a't :m:<&..;;oQ"i A IS B JINlf....J(IVT vfi:trof ~ ~1Jt! t '
l>~ A: 100 ~ W 'P' f11'fR1 111ff/W; ~ R'lf - (i;4 5'iiR t
(SRSWORl ll<i11 t ~ M 11 x ;m l1ll Ill ti'rt 'fit ilit & p iii/ :;w ffl( J6llffl ii'W1f t ;
•p,.2(10
l p, "S -""""'""" _ , ~ '"'g p; ->1/ I
2. P••P:iJFK.Jo~~f I
3. p. •1'1 ;f?.'f.:1.~~ ....~ tt C71fIJ:illf ~p1:Sig:wg f lll d) #IJI14 'ffll1"11 I
4. J7l tl'!l 57 ;m ~-? <Jtd sc'.-. ,.,., rrtr<fl?.FJif uf1 Jij··m iPfr., $to) w If""' ;: p;. '*f1'ff'f"1l
tfliN tiM 1
116. Jn 1 stn..,·cy to estimate the pro,,onion p of votes that & p<Orty will poll in an clt.'<:tion,
$latisti~,;iaus A ~nd B follow different sumplin~ suat~gies as follows:
St;),tistic:.i~ Sclcctl'i fi l'iirnple rnndom sample without ~phi.c~mtrll (SIU>WOR) of
200 vot1:1S, finds that x of them will 'Otc for the -pa.rty and estimate$ p by
'

45. 45
·Stali~ticlan R: Divides the-voters> list into Male and Female lists, selects lOO·from
each list by SRSWOR, firtds that .t1. x2 respectively will vote for the party and
estimates p by
x1 +x1
p,=zoo·
Th~; numberofvote~ in the (wo lists are the same. Then
1. P• is an unbiased estimate butp: i.s not.
2. PI andP2 are both unbiasod c:stimatc,s.
3. Pt and P'! &J'C·both unbiasedestimates. but P2 hasa smallervariMce than p1,or
the S.'lme v3riance asP•·
4. VariancesofPhP! are the same only if"the proportionsolroate.and tem.ale
voters who vote for the partyarc the ~me.
JJ7. I, 2, .... 5 l{ ~ 5 """"5"" l:t <'~"<: OW. f.J"'' """'~<a fii<Tti :
<!fey j : /l' 2, 3}; """)J: {l, 4, 5)
i't"T >i "*'1 ffl/W """I w(l l/f.?
I. 3/~ <f.<li! # I
2. ;;r{fo' r:;r. !).~ w IrrRfli t. r:rr. rnifi';;r. ~ ~ ;;f; ~ 'fftr.rr w;f.r.m ,J{'fiJ7(fl(5
(Gf ffffl11J Vi ff} 2d ?If 4ci /. 1
:>. 'hfililr<'RI. r.ffl11~ li<'lmr rt"' tt ll'f>r.1r'f t •"' w;tila 1'wr !fir{~ tfltritr 'ffl'l' 'ftf t 1
4. 1ft </; ruo; ~ - <ilfe '!.:" # I
111. Consider the fo11owing block design involving 5 treatments, labelled 1, 2, ..., s. and
two blocks:
Slock l: {1,2, 3); 8lockll: {l,4,S).
Which ofthe followingstatements is/arc tn1c'?
I. The design iscolUlected.
2. T'1e variance oflhe best linear unbiased estimatorofaoelementary treatment
contrast is either2<1or4cr2
• where o2
is the varianc-e ofan observation.
3. There is no non4
triviallinear function ofobservations coJlected through the
design whose expectation is identically equal to zero.
4. The degree~ offreedom a!>$ociat~d wilh the enor iszero.
I . 3/fi~R;'f "1fT -:tid/ <::FPJ} fffl?Vl :8 JiliMf =afl t;} ~111711 I
2. ~y 161 :fi<<li ~ )RrFj Ti /&If rrtfl'l} ~I I
3. """ """' w_.,>t'ff'l t. fW'il 'fffOI'I ~n f1l; >fiW '..''" t 1
4. ~- "1"1 ""' 1'11T ""' """' 0 't/1 I r.ro I

46. 46
1Ut Suppo~o~ ll1ou ''e: hav~ 3daLa set constst:ngof25 observt.lt<m1.where eoch value is e1lher 0 or L
TllC mean ofttt: dab cVlllot be': Ja!ger than the '~riancc.
2. 1kmc:u oflh: cbt2: WXOC. be Sttl3l~cr th3!:i the 'm~c~.
l The: me~ bctngsameas the variance implies th:lc the: mt2n tS1.t'ro.
J lhr &r*'« Mil b: 0 rfand only ifthe :':"Qn i~ etlhct 1or 0.
I 19. :z::r.m.1 ~ ~ "~l ~ 5. 4,11:1 - llo! S IS('(i 4xz-X1 S IS o) ~ ~ ::Rf W x :tO~ ;oc_.. 2:0 VY
~~ 1 fl!J•J ~ ff 411~-r 'HJ/?} tR'ZR ~ 1/f?
3'(1 • 2x: <~~t J,ofittli8'1 rfR t 25 r 2. 3x1 "'" 2x1 l1ii "~ rrr:r t ll i
3. ~'<1 I 2X: IM <~>tf qfWI';a Jt'R!tll?Pi "f#1 (.1 4. 3x,+2x: :m ttl!¢ ~ y.«r-t :rtf t J
119. ('on:o~elc.r thv ';iriab1es x, 2: 0 and X! ~ 0 s:uisfyint~ dtL~ con:ar.:unli x1 ·I• ~ ~ S, 4x, - x1 :S lS and 4x1
- x1 ~ IS. Which .,fthc follt,wingstatements isfa~ OOI'r>ect'l
I. 111e m:u.tmumvain.:of3x1 + 2x: !s25 2. 'l1le .uinunum value of3x1 t- 2X! is II
'· :l>c1<1 2x: hasno f1m1e m.:nimum 4. Jxf+ 2>.1 hitS no fitLite n:Uniuu.:m
110. ~ """ "',/ f"' V'fkll ~ 'IF¥ R; ~ """' '~fit 1lfit 12 fir.« 4 't"' lll1Rit ol ..,; # v>
"""' mr - 'ila ¢it 8 fll·ri: ,; "' >!>:~' <l 117 OJ!1iV # I ofl: _ , 'lfll 20% ~ t i!t
tunll ,JI.4IWI 4
I. ~ tf ~ ;;J; r.:uJ ?frF.8 ~ 41.kt 2 /. I
2. Y.,'f.th 4 ~~nr;r,1 ;J4 !G!~ rfrprj ii 1iOtJ 4 t I
3. ~ it tll4tb f;m Rffrrnrrrn :r.«"'T ?J'l!'ll it ;;.;pr 16 ~ t 1
4. Sf",'fA il Vftrrh tflY.'I fitd;IIJ )fl/1 i{J<:"l tflflr i/ ~ 24 ~ t I
120. In a S)'Siom with o smglc SC:.'>'er. s~ppOSc thot t u$tOmerS nrrive m a Poisson rote of I person
.::very 12 minlltCS and arc .scrvtoc'<J ut the Poisson r.ue of 1scrvic(! eve!')' 8 m.imues. If•he
orrivt~l ~l<lnl<:renscs hy 20% 1hcn in the s1csdy st:uc
I.
'..3.
J.
the lncrc:a~c in the average number ofcus1omcrs in the syst<:m is 2.
the mcrt:II$C nl the :l'Cntgc:tMnbc!'oicus•omcrs in lh<: t.y~1cn I~ 4•
the UIC-rcasc 111 the average tim:: spent by a custOtl<er in Lhe system itt 16 mimttcs.
Ihe tncreasc in the average1imc spent b)' a customer in tJ1c 'Yftcm '' 24 minute$,
•

47. II
-------------------------------------------------------------
I • ANSWER KEY ON THE BASIS
MATHEMATICAL
SCIENCES
~--q;f I
ANSWER SHEET
~
Serial No.
Roll Number
1··.··. · 1.····..·. 1· ·1····..··. 1·. ·1·.··.·1. . ; ~ .. .i . : j.. .i : . ~ t.. ..;
CD CD CDCD CDCD
® ® ®® ®®
0 0 00 00
0 0 00 00
® ® ®® ®®
® ® ®® ®®
0 0 00 00
® ® ®® ®®
® ® ®® ®®
® ® ®® ®®
...... --'li."lli. ~/ANSWER
Q.No.
CD ® 0 0
1 0
• 0 0
2 0 a 0 0
3 0 0 e 0
4
• 0 0 0
5 0 0 0
6 0 0
• 0
7 0 0 0
•8 0 0
• 0
9
• 0 0 0
10 0 0 0
•11 0 0 0
•12 0 0
• 0
13 0
• 0 0
14
• 0 0 0
15 0
• 0 0
16 0 0 0
•17 0 0 0
18 0 ~ 0 0
19
• 0 0 0
20 0 0 ~ 0
.. .I
1:n 1., 11
21 0 ~ 0 0
22 0 0 0
23 0 a 0 0
24 0 0 0
•25 0 0
• 0
26
• 0 0 0
27 0 0
• 0
28 0
• 0 0
29 0 0 0
30 0 0
• 0
31 0 0
• 0
32 0 0 0
•33
• 0 0 0
34
• 0 0 0
35 0
• 0 0
36 0 0 0
•
Booklet Code Medium
D
@
®
© ®
SubjectCode Centre Code
[§] rn. .
CDCD
®®
00
00
®®
®®
00
®®
®®
®®
ANSWER COLUMNS
'!i.'lli. ~I ANSWER 'li.'lli. ~I ANSWER
lfliO- 2
SIDE- 2
~8J'fl <l; ~ 00
INSTRUCTION FOR INVIGILATOR
¥fliT m~m m ~ ~ -oo ~.
m ~em, ~em, ~em
q mw:lf <fi mim <tl ~ Cfi ~I
Check Roll Number, Booklet Code,
Subject Code, Centre Code & Signature ol
Candidate before signing.
~~ I Slgnatureollnvlgllator
'!i.'l!i. ~/ANSWER
Q.No. CD ® 0 0 Q.No. CD ® 0 0 Q.No.
CD ® 0 0
37 0 0 • 0
38 0
39 0
40 0
41 0 •
42 0 0
43 0 0
44 0 0
45 0 0
46 0 0
47 0 •
48 • •
49 0
50 0 @
51 0 0
52 0 ~
53 0
54 0 0
55 0 0
56 0 0
57 0
58 0 •
59 0 •
60 0 0
61 0
62 0
s3 e 0
0 0
0 0
0 0
0 0
• 0
0
0
~ 0
0 •
0 0
0 0
0 0
0 0
0 •
0 0
0 0
0
0
0 <0
0 0
0 0
0 0
0
0 @
• 0
64 • 0 • 0
0
OJ
0
0
s5 e
66 0
67
68 ~
69 0
70 •
71 •
72 0
• 0
• 0
~ 0
• 0
• 0
0 •
0 0
~ 0
0
0
0
73 • 0 • 0
74 0 @ 0 (I
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
0 • 0
0
~ 0 •
0
<t 0 •
.~
• • 0
0
• 0 0
0 0 ~
0 ~ ()
• • 0
@ 0 •
0 0 0
0 0 •
0 0 •
• 0
• • G1!J
0 I)
0 0 •
0
0 0
•0
0
0
0
0
0
0
0
@
0
•0
••0
0
®
0
0
0
0
97 0 0 • f)
98 0 • • 0
99 •ooe
100 •
101 •
102 •
103 0
104 0
105 0
106 0
107 •
108 0
109 0
t1
•••0
~
0
0
•0
••
•0
0
0
••••
0
•e
•0
••0
••
110
• tll 0
•111 0 0
• 0
112 0
• 0
113 0
• • •114
• • • 0
115
• 0
• •116 0
• • 0
117
• • • •118 0
• • •119
• • 0 0
120
• 0
• 0
II
rrz
CD 0
--:::CD
ro:IJa.o
s·=
... z:JC
CD 3
0"0"
0 CD
X_....,
co enCllc
err(/)~·
-·CD::I (")
co-
,..()
:TO
co a.
-oCD
ll>Ro
::+o
~ CD
::I ::I
-co-.-·CD
~()
::I 0
ll>a.
Cll CD
.. (/)
:J
0
c
a: