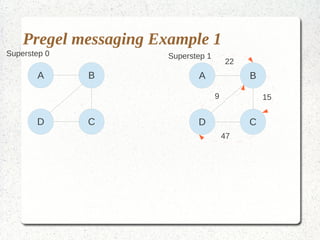
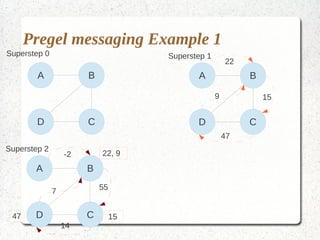
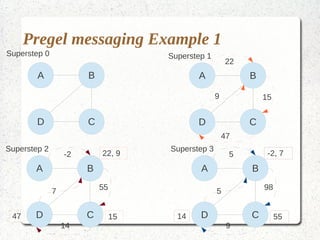
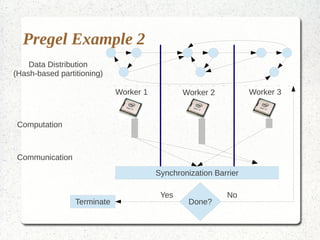
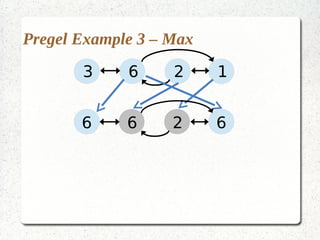
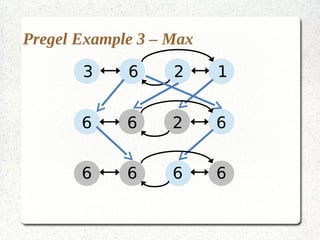
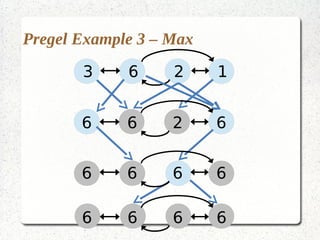
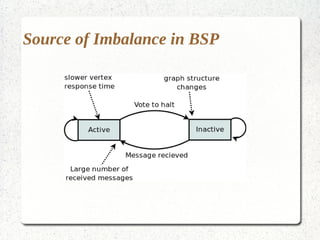
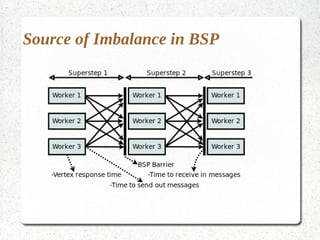
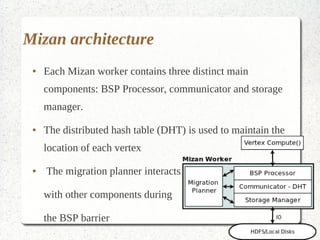
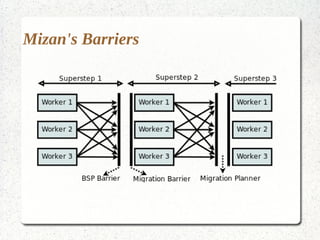
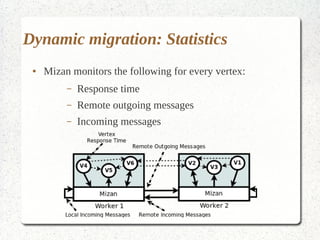
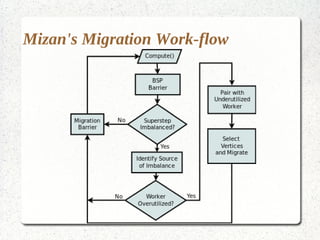
This document discusses large-scale graph processing and the challenges involved. It introduces Pregel, an influential graph processing system based on the bulk synchronous parallel model. Key aspects of Pregel are explained such as its vertex-centric approach, use of supersteps with messaging between steps, and guarantees of message delivery. The document also discusses Mizan, a graph processing system developed locally that aims to improve load balancing through dynamic graph partitioning between supersteps. Examples of graph algorithms like PageRank and Max are provided in the Pregel and Mizan models. Finally, the class is assigned to install and run Mizan on a single machine following an online tutorial.

1. King Abdullah University of Science and
Technology
CS348: Cloud Computing
Large-Scale Graph Processing
Zuhair Khayyat
10/March/2013

2. The Importance of Graphs
● A graph is a mathematical structure that represents pairwise
relations between entities or objects. Such as:
– Physical communication networks
– Web pages links
– Social interaction graphs
– Protein-to-protein interactions
● Graphs are used to abstract application-specific features into a
generic problem, which makes Graph Algorithms applicable to
a wide variety of applications*.
*http://11011110.livejournal.com/164613.html

3. Graph algorithm characteristics*
● Data-Drivin Computations: Computations in graph
algorithms depends on the structure of the graph. It is hard to
predict the algorithm behavior
● Unstructured Problems: Different graph distributions
requires distinct load balancing techniques.
● Poor Data Locality.
● High Data Access to Computation Ratio: Runtime can be
dominated by waiting memory fetches.
*Lumsdaine et. al, Challenges in Parallel Graph Processing

4. Challenges in Graph processing
● Graphs grows fast; a single computer either cannot fit a large
graph into memory or it fits the large graph with huge cost.
● Custom implementations for a single graph algorithm requires
time and effort and cannot be used on other algorithms
● Scientific parallel applications (i.e. parallel PDE solvers)
cannot fully adapt to the computational requirements of graph
algorithms*.
● Fault tolerance is required to support large scale processing.
*Lumsdaine et. al, Challenges in Parallel Graph Processing

5. Why Cloud in Graph Processing
● Easy to scale up and down; provision machines
depending on your graph size.
● Cheaper than buying a physical large cluster.
● Can be used in the cloud as “Software as a services” to
support online social networks.

6. Large Scale Graph Processing
● Systems that tries to solve the problem of processing large
graphs in parallel:
– MapReduce – auto task scheduling, distributed disk
based computations:
● Pegasus
● X-Rime
– Pregel - Bulk Synchronous Parallel Graph Processing:
● Giraph
● GPS
● Mizan
– GraphLab – Asynchronous Parallel Graph Processing.

7. Pregel* Graph Processing
● Consists of a series of synchronized iterations
(supersteps); based on Bulk Synchronous Parallel
computing model. Each superstep consists of:
– Concurrent computations
– Communication
– Synchronization barrier
● Vertex centric computation, the user's compute() function
is applied individually on each vertex, which is able to:
– Send message to vertices in the next superstep
– Receive messages from the previous superstep
*Malewicz et. al., Pregel: A System for Large-Scale Graph Processing

8. Pregel messaging Example 1
Superstep 0
A B
D C

9. Pregel messaging Example 1
Superstep 0 Superstep 1
22
A B A B
9 15
D C D C
47

10. Pregel messaging Example 1
Superstep 0 Superstep 1
22
A B A B
9 15
D C D C
47
Superstep 2
-2 22, 9
A B
7 55
47 D C 15
14

11. Pregel messaging Example 1
Superstep 0 Superstep 1
22
A B A B
9 15
D C D C
47
Superstep 2 Superstep 3
-2 22, 9 5 -2, 7
A B A B
7 55 5 98
47 D C 15 14 D C 55
14 9

12. Vertex's State
● All vertices are active at superstep 1
● All active vertices runs user function compute() at any
superstep
● A vertex deactivates itself by voting to halt, but returns to
active if it received messages.
● Pregel terminates of all vertices are inactive

13. Pregel Example 2
Data Distribution
(Hash-based partitioning)
Worker 1 Worker 2 Worker 3
Computation
Communication
Synchronization Barrier
Yes No
Terminate Done?

14. Pregel Example 3 – Max
3 6 2 1

15. Pregel Example 3 – Max
3 6 2 1
6 6 2 6

16. Pregel Example 3 – Max
3 6 2 1
6 6 2 6
6 6 6 6

17. Pregel Example 3 – Max
3 6 2 1
6 6 2 6
6 6 6 6
6 6 6 6

18. Pregel Example 4 – Max code Vertex value
class
Class MaxFindVertex:public Vertex<double, void, double> { Edge value class
public:
Message class
virtual void Compute(MessageIterator* msgs) {
int currMax = GetValue(); Send current Max
SendMessageToAllNeighbors(currMax);
Check messages
for ( ; !msgs­>Done(); msgs­>Next()) { and store max
if (msgs­>Value() > currMax)
currMax = msgs­>Value();
Store new max
}
if (currMax > GetValue())
*MutableValue() = currMax;
else VoteToHalt();
}
};

19. Pregel Message Optimizations
● Message Combiners:
– A special function that combines the incoming
messages for a vertex before running compute()
– Can run on the message sending or receiving worker
● Global Aggregators :
– A shared object accessible to all vertices. that is
synchronized at the end of each superstep, i.e., max
and min aggregators.

20. Pregel Guarantees
● Scalability: process vertices in parallel, overlap
computation and communication.
● Messages will be received without duplication in any
order.
● Fault tolerance through check points

21. Pregel's Limitations
● Pregel's superstep waits for all workers to finish at the
synchronization barrier. That is, it waits for the slowest
worker to finish.
● Smart partitioning can solve the load balancing problem
for static algorithms. However not all algorithms are
static, algorithms can have a variable execution behaviors
which leads to an unbalanced supersteps.

22. Mizan* Graph Processing
● Mizan is an open source graph processing system, similar
to Pregel, developed locally at KAUST.
● Mizan employs dynamic graph repartitioning without
affecting the correctness of graph processing to
rebalanced the execution of the supersteps for all types of
workloads.
*Khayyat et. al., Mizan: A System for Dynamic Load Balancing in Large-scale
Graph Processing

23. Source of Imbalance in BSP

24. Source of Imbalance in BSP

25. Types of Graph Algorithms
● Stationary Graph Algorithms:
– Algorithms with fixed message distribution across superstep
– All vertices are either active or inactive at same time
– i.e. PageRank, Diameter Estimation and weakly connected
components.
● Non-stationary Graph Algorithms
– Algorithms with variable message distribution across supersteps
– Vertices can be active and inactive independent to others
– i.e. Distributed Minimal spanning tree

26. Mizan architecture
● Each Mizan worker contains three distinct main
components: BSP Processor, communicator and storage
manager.
● The distributed hash table (DHT) is used to maintain the
location of each vertex
● The migration planner interacts
with other components during
the BSP barrier

27. Mizan's Barriers

28. Dynamic migration: Statistics
● Mizan monitors the following for every vertex:
– Response time
– Remote outgoing messages
– Incoming messages

29. Dynamic migration: planning
● Mizan's migration planner runs after the BSP barrier and creates a
new barrier. The planning includes the following steps:
– Identifying unbalanced workers.
– Identifying migration objective:
● Response time
● Incoming messages
● Outgoing messages
– Pair over-utilized workers with underutilized
– Select vertices to migrate

30. Mizan's Migration Work-flow

31. Mizan PageRank Compute() Example
void compute(messageIterator<mDouble> * messages, userVertexObject<mLong, mDouble,
mDouble, mLong> * data,messageManager<mLong, mDouble, mDouble, mLong> * comm) {
double currVal = data­>getVertexValue().getValue();
double newVal = 0; double c = 0.85;
while (messages­>hasNext()) {
double tmp = messages­>getNext().getValue(); Processing
newVal = newVal + tmp; Messages
}
newVal = newVal * c + (1.0 ­ c) / ((double) vertexTotal);
mDouble outVal(newVal / ((double) data­>getOutEdgeCount()));
if (data­>getCurrentSS() <= maxSuperStep) {
for (int i = 0; i < data­>getOutEdgeCount(); i++) { Termination
comm­>sendMessage(data­>getOutEdgeID(i), outVal);
data­>getOutEdgeID(i); Condition
}
} else {
data­>voteToHalt();
} Sending to
Neighbors
data­>setVertexValue(mDouble(newVal));
}

32. Mizan PageRank Combiner Example
void combineMessages(mLong dst, messageIterator<mDouble> *
messages,messageManager<mLong, mDouble, mDouble, mLong> * mManager) {
double newVal = 0;
while (messages­>hasNext()) {
double tmp = messages­>getNext().getValue();
newVal = newVal + tmp;
}
mDouble messageOut(newVal);
mManager­>sendMessage(dst,messageOut);
}

33. Mizan Max Aggregator Example
class maxAggregator: public IAggregator<mLong> {
Public:
mlong aggValue;
maxAggregator() {
aggValue.setValue(0);
}
void aggregate(mLong value) {
if (value > aggValue) {
aggValue = value;
}
}
mLong getValue() {
return aggValue;
}
void setValue(mLong value) {
this­>aggValue = value;
}
virtual ~maxAggregator() {}
};

34. Class Assignment
● Your assignment is to configure, install and run Mizan on
a single Linux machine throw following this tutorial:
https://thegraphsblog.wordpress.com/mizan-on-ubuntu/
● By the end of the tutorial, you should be able to execute
the command on your machine:
mpirun ­np 2 ./Mizan­0.1b ­u ubuntu ­g web­Google.txt ­w 2
● Deliverables: you store the output of of the above
command and submit it by Wednesday's class.
● Any questions regarding the tutorial or to get an account
for a Ubuntu machine, contact me on:
zuhair.khayyat@kaust.edu.sa