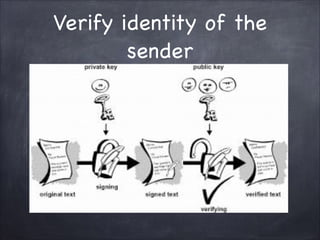
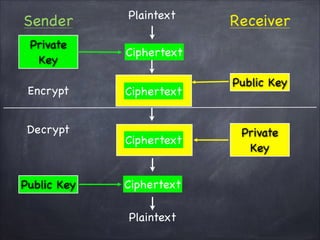
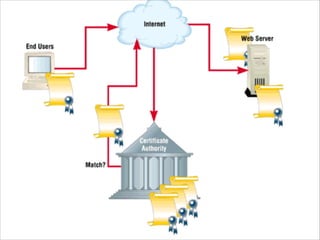
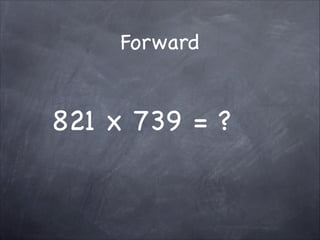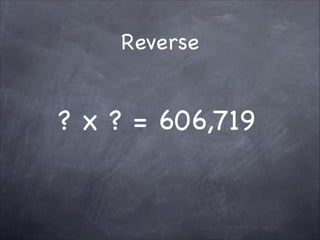The document provides an overview of cryptography, detailing classical ciphers like transposition and substitution methods, and highlighting modern techniques such as asymmetric cryptography and hybrid systems. It explains the intricacies of mechanisms like the Vigenère cipher and RSA encryption, emphasizing the mathematical underpinnings of key exchanges and encryption methods. Additionally, it discusses the roles of digital signatures and certificate authorities in ensuring authenticity and integrity in digital communications.

1. Domain 6: Cryptography
“the art and science of concealing meaning”

2. Cryptography
comes from the Greek word meaning “secret
writing”
scrambling some kind of useful information
called plaintext
into a garbled form
called ciphertext
goal is to allow two or more parties to
communicate the information while preventing
other parties from being privy to it

3. Cryptosystem
set of plaintexts
set of keys
set of ciphertexts
enciphering functions
plaintext * key
deciphering functions
ciphertext * key

4. Two types of Classical
Ciphers
Transposition
Substitution

5. Transposition
Rearranges the characters in the plaintext to
form the ciphertext
the letters are not changed

6. Transposition example
rail fence cipher
composed by writing the plaintext in two rows,
proceeding down, then across
H
E
L
L
O
W
O
R
L
D
then read the ciphertext across, then down
HWEOLRLLOD

7. Characteristics of a
Transposition Cipher
the same characters used in the plaintext are also
used in the ciphertext
the letters are simply in a different spot (appear
jumbled)

8. Substitution Cipher
Vxevwlwxwlrq Flskhu

9. Substitution Cipher
Changes characters in the plaintext to produce
the ciphertext
Examples
Caesar cipher
Vigenere Cipher
One-time pad

10. Caesar cipher
Not very complex
didn’t need to be during the time since few
people knew how to read
therefore it was very effective

11. KHOOR ZRUOG
-3 letters
HELLO WORLD
Caesar cipher

12. Too easy to crack!
Substitution and transposition ciphers do not
disguise the linguistic patterns of letters and
word frequency

13. Solution
Use both substitution and transposition ciphers
together
First encrypt with one then encrypt the
cipher text with the other
Modern computer cryptography has made the
most of this

14. Vigenere Cipher
Complex substitution cipher
Doesn’t use a one-to-one relationship between each
letter and its substitute
There is a one-to-many relationship between each letter
and its substitute
Based on the table found on the next slide

15. Vigenere

16. Vigenere Cipher table
Each row of the table corresponds to a Caesar
cipher
First row is a shift of 0
Second is a shift of 1
Last is a shift of 25

17. Vigenere Cipher Process
The Vigenere cipher uses the previous table together
with a keyword to encipher a message
Length of the key is called the period of the cipher
Each letter in the keyword is used to determine how
much to shift the corresponding letter in the message

18. 1.Write down the plaintext message
S TUDY STUD YST UDYST UDYS
I WILL PASS THE CISSP EXAM
2.Write keyword above the plaintext, repeated as many
times as necessary
3.In the table, find the intersection of each row (keyword
letter) and column (plaintext letter) to determine the
ciphertext letter

19. Vigenere

20. 1.Write down the plaintext message
S TUDY STUD YST UDYST UDYS
I WILL PASS THE CISSP EXAM
2.Write keyword above the plaintext, repeated as many
times as necessary
3.In the table, find the intersection of each row (keyword
letter) and column (plaintext letter) to determine the
ciphertext letter
A PCOJ HTMV RZX WLQKI YAYE

21. Decrypting
Write the keyword repeatedly above the message
A PCOJ HTMV RZX WLQKI YAYE
S TUDY STUD YST UDYST UDYS
Use the keyword letter to pick a column of the table, and
then trace down the column to the row containing the
ciphertext letter
The index of that row is the plaintext letter

22. Vigenere

23. Result
S TUDY STUD YST UDYST UDYS
A PCOJ HTMV RZX WLQKI YAYE
I WILL PASS THE CISSP EXAM

24. Weakness???
Pruvian cavalry officer named Kasiski noticed a weakness
repetitions occur when characters of the key appear
over the same characters in the ciphertext
!
!
Key: VIG VIG VIG VIG VIG
Plaintext: THE BOY HAS THE BAG
Ciphertext: OPK WWE CIY OPK WIM

25. Weakness???
The ciphertext repetitions are 9 characters
apart
The key must be a multiple of 9
Key: VIG VIG VIG VIG VIG
Plaintext: THE BOY HAS THE BAG
Ciphertext: OPK WWE CIY OPK WIM

26. Weakness???
Examine the text for multiple repetitions
Tabulate their length and the number of characters
between successive repetitions
From the repetitions, establish the probable key
length
Tabulate the characters for each key letter
separately and solve each as a Caesar cipher

27. Asymmetric Cryptography

28. Alice and Bob
Want to send a secret message through the
public mail
Two scenarios…

29. First approach
Bob gives Alice a copy of his padlock key
Alice puts the secret message in a box
she locks the box using the key padlock
she then sends the box to Bob through regular
mail
when Bob receives the box, he uses his copy of
Alice's key to open the box

30. Second approach
Alice asks Bob to send his open padlock to her
through regular mail, keeping his key to himself
When Alice receives it she uses it to lock a box
containing her message, and sends the locked
box to Bob
Bob can then unlock the box with his key and
read the message from Alice.

31. Asymmetric Cryptography
Also referred to as public key cryptography
Concept introduced by Whitfield Diffie and Martin
Hellman in 1976

32. Basic Idea
Each user has a public key and a private key
Sender and receiver do not need to share a
secret key
All communication involves the public key
one key "locks" a lock; while the other is
required to unlock it

33. How can this work?
The two keys are linked to each other
mathematically
The algorithm involves fairly sophisticated
mathematics
numbers theory
finite fields
abelian groups
elliptic curves

34. Sending a message
The sender would use the receiver’s public key to
encrypt the message
The receiver would then use his private key to decrypt
the message

35. Advantages
Don’t need to worry about key distribution
Key scalability
each person has one matched key pair
don’t need one distinct key for each
communicating pair of users

36. Disadvantage
Very slow to process
algorithms are computationally intensive
because of the mathematics involved
can be up to 1000 times slower (in terms of
bytes per second) than symmetric key
algorithms

37. Solution:
Hybrid Systems
Use symmetric and asymmetric key algorithms
where each is strong

38. Hybrid Example
Use symmetric key cryptography to encrypt a
long message
Use asymmetric key cryptography to exchange
the symmetric key used in the encryption
process

39. Asymmetric Key Cryptography Algorithm
First invented by researchers in the British military
but unclassified recently
James Ellis was the cryptographer that is credited with
its creation, but was unable to implement the idea
Clifford Cocks created what is known as the RSA
encryption algorithm out of Ellis’ idea
Considered the most important advance in
cryptography in the past 2000 years

40. One-Way Function
“forward versus reverse”
Function in which there is an enormous
difference in the time required to perform the
function itself compared to how quickly you can
perform its inverse

41. Forward
821 x 739 = ?

42. Reverse
? x ? = 606,719

43. RSA encryption algorithm
developed by Ron Rivest, Adi Shamir, Leonard
Adleman
based on the fact that you can easily and fairly
quickly multiply two large prime numbers together
but it takes a very long time to factor that number
into its two prime factors
if the product is large enough (500 digits) then there is
a factor of millions or billions difference in time required

44. Private and Public keys
are mathematically related to each other through one-way
functions
in theory it is possible to derive one from the other

45. Private and Public keys
to create the key pair you perform the trapdoor in the
fast direction (multiplying the two large prime numbers
together)

46. Private and Public keys
to crack the private key you must perform the one-way
function in the slow direction
factoring the product into its two prime factors
the larger the key, the greater the difference between
the efforts necessary to compute the function in the
forward and inverse directions

47. Another use of
Asymmetric Key
Cryptography
Verify the identity of the sender of a
message

48. Verify the identity of the
sender
sender of the message would encrypt the message using
his own private key
receiver uses the sender’s public key to decrypt the
message

49. Another use of
Asymmetric Key
Cryptography
Verify the identity of the sender of a message
AND
provide confidentiality
Yet

50. Verify the identity of the sender
and provide confidentiality
involves two encrypting steps
1. encrypt first using the sender’s private key
2. encrypt again using the receiver’s public key
two decrypting steps
1. decrypt with his own private key
2. decrypt again using the sender’s public key

51. Verify identity of the
sender

52. Public Key
Private
Key
Private
Key
Public Key
Plaintext
Sender Receiver
Ciphertext
Ciphertext
Ciphertext
Ciphertext
Plaintext
Decrypt
Encrypt

53. Digital Signatures and
Certificate Authorities

54. Digital Signatures
Used to authenticate computer-based business
information
Used to
detect unauthorized modifications to data
authenticate the identity of the creator

55. Provides Non-repudiation
recipient can use a digital signature to prove to
a third party that the signature was in fact
generated by the signatory

56. Uses public key
cryptography
private key
used in creating the digital signature
public key
used in verifying the digital signature

57. Digital signature
verification
process of checking the digital signature by
reference to the original message and a given
public key

58. Certificate Authorities
a trusted third party that associates an
identified signer with a specific public key

59. Certificate Authority