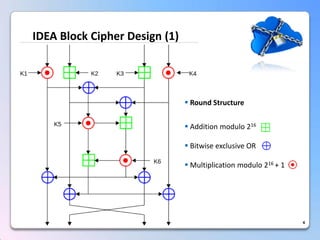
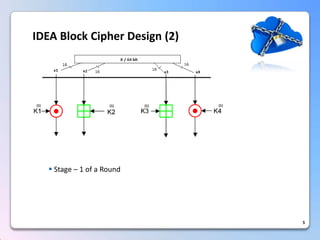
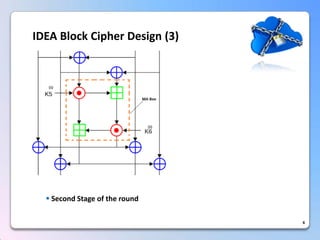
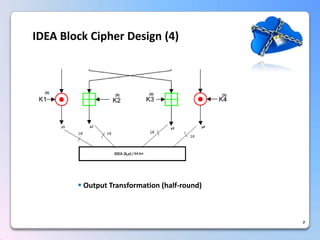
This document summarizes a timing attack against the IDEA block cipher. It describes how precise timing measurements of encryptions can reveal information about the secret key. The attack analyzes timing differences between encryptions to determine when operations like multiplication involve a zero value. This leaks key bits over multiple rounds of the analysis. The attack can recover the full 128-bit key without knowledge of the plaintext.

1. Cryptanalytic Timing Attacks against IDEA Product block cipher
(Ref: "Side Channel Cryptanalysis of Product Ciphers" by John Kelsey , Bruce Schneier , David Wagner , and Chris Hall in September 1998 )
Srilal Buddika

2. Outline
1.Motivation
2.About IDEA
3.IDEA Block Cipher Design
4.Cryptanalytic History on IDEA
5.Timing Attack against IDEA
6.Conclusion
7.Discussion
2

3. 3About IDEA
IDEAstands for International Data Encryption Algorithm (1991)
IDEA is Block Cipher
Block Size : 64 bits
Key Size : 128 bits
8Rounds + Output Transformation (half-round)
WhyIDEA ?
The algorithm was designed to achieve high data throughput for use in real-time communications system, especially for wireless communication

4. 4IDEA Block Cipher Design (1)
RoundStructure
Additionmodulo216
BitwiseexclusiveOR
Multiplicationmodulo216+1

5. IDEA Block Cipher Design (2)
5
Stage–1ofaRound

6. 6IDEA Block Cipher Design (3)
SecondStageoftheround

7. 7IDEA Block Cipher Design (4)
OutputTransformation(half-round)

8. 8IDEA Block Cipher Design (5)
KeyGeneration
KeySize=128bit
Sub-keySize=16bit
i.e.SimplyKeydividedintoeightpieces
Algorithm:
1.Take1steightsub-keys
2.Thenrotatethekey25bitstotheleft
3.Repeatthestep-1

9. 9
Cryptanalytic History on IDEA
Consideredasreallysecure
BestattackcanbreakIDEAreducedto6rounds(FullIDEA=8.5rounds)
WeakKeyproblemwithtoomany0-bits(ExposedtoSide-ChannelAttacks)

10. 10
IDEAcanbecryptanalyzedwithapieceofside-channelinformation
E.g.Whetheroneoftheinputsintooneofthemultiplicationsiszero
Timingscanbeacquiredintwosimpleways:
1.The cryptanalyst makes extremely precise timings of each encryption (A Ciphertext-Only Timing Attack)
2.The cryptanalyst measures total time to encrypt many similar plaintext blocks at a time (An Adaptive Chosen Plaintext Timing Attack) Timing Attack against IDEA (1)

11. 11Timing Attacks against IDEA (2) Attacking Scenario
1.Recordprecisetimingsfornencryptions.AlsostoretheresultingciphertextblocksandletT0..n-1bethetimings,andC0..n-1betheciphertextblocks.
2.Grouptheciphertextblocksandtimingsinto216subsets,basedonthelow- order16bitsoftheoutput.
3.Testtheaveragetimesofeachgroupagainsttheaveragetimesofallthegroupsstatistically,tofindwhetheroneofthesetshas(withsomeacceptablyhighprobability)aloweraveragethantheothersets.
4.Ifso,thentheinputstothelastmultiplyoftheoutputtransformationmusthavebeen0forallinputsinthatset.Hencesolveforthelastmultiplicativesub-key.

12. 12Timing Attacks against IDEA (3)
5.Ifthereisnodifference,theneitherwe'vechosensomeparameters(i.e.,n) wrong,orthesub-keyisa0.
6.Repeatsteps2-3,above,forthehigh-order16bitsandsolvethefirstmultiplicativesub-keyoftheoutputtransformation.Wenowhave32bitsofexpandedkey.
7.Wenowattackthesecondadditivesub-keyintheoutputtransformation. Foreachpossiblevalueofthissub-key,welookatwhichciphertextblocksleadustoazerovaluegoingintothefirstmultiplicationofthelastround'sMAbox.
8.Foroneofthesesub-keyguesses,theaveragetimingshouldbelessthanforalltheothersub-keyguesses.Thisrevealstherightsub-key.
9.Ifthereisnodifference,theneitherwe'vechosensomeparameterswrong, orthefirstsub-keyintheMA-boxiszero.Wehavenowrecovered48bitsofexpandedkey.

13. 13Timing Attacks against IDEA (4)
10.Wenowattackthefirstadditivesub-keyintheoutputtransformation,andthefirstsub-keyintheMA-box.Wedothisasfollows:
Breaktheciphertextblocksandtimingsupinto216subsetsbasedonthevalueoftheleftmost(first)inputtotheMA-box
Foreachpossiblesub-keyvalueforthefirstadditivesub-keyoftheoutputtransformation,breakeachsubsetupinto216sub-subsets,basedonwhatthevalueofthesecondMA-boxinputwouldbeifthisweretherightsub-key
Fortherightsub-key,eachsubsetwillhaveonesub-subsetwhichhasasmallertimingvaluethanalltheothersub-subsetsinthatsubset.Wehavenowfound64bitsofsub-key
Wenowchooseanythreeofthesesub-subsets,andusethemtosolveforthefirstmultiplicativesub-keyoftheMA-box.Wehavenowfound80bitsofsub- key
Finally,wecanbrute-force/exhaustivesearchtheremaining48bits.(Therearealsootherwaystocontinuethisattack)

14. Conclusion14
ThiskindofattackmightalsobepracticalforrecoveringthekeyfromaCipherswhichalwaysencryptsunderthesameIDEAkey.Thecryptanalystortheattackerdoesnotneedtoknowanythingabouttheplaintextforthisattack,butmustalwaysknowpreciselywhentheencryptionstartedandwhenitendedwiththecollectedciphertextblocks.
There'ssomethingimportanttoknowthat,thisisnottheonlysidechannelthatcandiscoverthiskindofinformationbutthingslikeradiationandpowerconsumptioncanalsoleakthismultiply-by-zerocondition.

15. Thank You ! 15