Credit default swaps (CDS) are contracts that transfer credit risk from one party to another. A CDS controls credit risk, while an interest rate swap controls interest rate risk. If a reference entity experiences a credit event like default, the protection seller compensates the buyer. Restructuring is a controversial credit event because it can trigger a payout even for routine debt restructurings. A CDS has an option-like payoff because payment depends on a credit event occurring. For asset-backed securities, the focus is on cash flow adequacy rather than bankruptcy. Physical settlement of a CDS involves delivery of the reference obligation, while cash settlement involves a payment equal to the price difference.

1. 1
CHAPTER 32 – Credit Default Swaps
1. How does the role of a credit derivative differ from that of an interest-rate swap in terms of controlling
risk?
A credit derivative controls credit risk. An interest rate derivative controls interest rate risk.
A credit derivative is a contract in which the protection buyer pays a fee to the protection seller. If a
reference-security credit event occurs, the protection seller buys the bond from the protection buyer for par
value and the protection buyer delivers the bond. Since the reference security is now worth less than par, the
protection sell incurs a loss equal to par less the after-credit-event value of the reference security. For
example, if the issuer is in default (a credit event) and the (present value of the) expected recovery rate for the
reference security (a bond for example) is 40%, then the market price of the bond will be 40.00. The
protection seller would incur a 100 – 40 = 60 loss and the protection buyer would receive par value.
An alternative arrangement between the protection buyer and protection seller is that the protection seller just
pays the protection buyer $60 cash.
This contract is a securitized derivative whose value is derived from the credit risk on an underlying reference
security: a bond, loan or any other financial asset. If the likelihood of a credit even increases, the value of the
credit derivative increase.
Please see the Chapter 5, Question 26 homework for a discussion of interest rate swaps. Be sure you
understand the difference between an interest rate swap and the CDS.
2. Why is a portfolio manager concerned with more than default risk when assessing
a portfolio’s credit exposure?
“Credit risk” includes three types of risk:
(i) Default Risk: the risk that the issuer will default
(ii) Credit Spread Risk: the risk that the credit spread for the rating category will increase
(iii) Downgrade Risk: the risk that an individual issue will be downgraded
3. Answer the below questions.
(a) What is meant by a reference entity?
The International Swap and Derivatives Association (ISDA) produces and the standard contracts upon
which most credit default swaps rely. The standard ISDA CDS agreement will identify the reference
entity and the reference obligation. The reference entity is the issuer of the debt instrument and hence also
referred to as the reference issuer.
It could be a corporation or a sovereign government. For Example the reference entity could be Vail
Resorts, Inc. the Boulder Valley School District.
(b) What is meant by a reference obligation?
The reference obligation, also referred to as the reference asset, is the particular debt issue for which the
credit protection is being sought. For example, if the reference entity is Vail Resorts, then the reference
obligation would be the 6.50% bonds of 2019.

2. 2
4. What authoritative source is used for defining a “credit event”?
The International Swap and Derivatives Association (ISDA) provide definitions of what credit events are. The
1999 ISDA Credit Derivatives Definitions (referred to as the “1999 Definitions”) provides a list of eight credit
events:
(1) bankruptcy
(2) credit event upon merger
(3) cross acceleration
(4) cross default
(5) downgrade
(6) failure to pay
(7) repudiation or moratorium
(8) restructuring
These eight events attempt to capture every type of situation that could cause the credit quality of the
reference entity to deteriorate, or cause the value of the reference obligation to decline.
In January 2003, the ISDA published its revised credit events definitions in the 2003 ISDA Credit Derivative
Definitions (referred to as the “2003 Definitions”). The revised definitions reflected amendments to several of
the definitions for credit events set forth in the 1999 Definitions. Specifically, there were amendments for
bankruptcy, repudiation, and restructuring.
The major change was to restructuring, whereby the ISDA allows parties to a given trade to select from
among the following four definitions:
(1) no restructuring;
(2) “full” or “old” restructuring, which is based on the 1993 Definitions;
(3) “modified restructuring,” which is based on the Supplement Definition;
(4) “modified restructuring.”
The last choice is new and was included to address issues that arose in the European market.
5. Why is “restructuring” the most controversial credit event?
The most controversial credit event that may be included in a credit default swap is restructuring of an
obligation. A restructuring occurs when the terms of the obligation are altered so as to make the new terms
less attractive to the debt holder than the original terms. The terms that can be changed would typically
include, but are not limited to, one or more of the following:
(1) a reduction in the interest rate
(2) a reduction in the principal
(3) a rescheduling of the principal repayment schedule (e.g., lengthening the maturity of the obligation)
or postponement of an interest payment
(4) a change in the level of seniority of the obligation in the reference entity’s debt structure.
The reason why restructuring is controversial is that a protection buyer profits from the inclusion of a
restructuring as a credit event and feels that eliminating restructuring as a credit event will erode its credit
protection.
The protection seller, in contrast, would prefer not to include restructuring since even routine modifications of
obligations that occur in lending arrangements would trigger a payout to the protection buyer.
Moreover, if the reference obligation is a loan and the protection buyer is the lender, there is a dual benefit for
the protection buyer to restructure a loan. First, the protection buyer receives a payment from the protection

3. 3
seller. Second, the accommodating restructuring fosters a link between the lender (who is the protection
buyer) and its customer (the corporate entity that is the obligor of the reference obligation).
6. Why does a credit default swap have an option-type payoff?
A credit default swap is similar to an option (and therefore has an option-type payoff) because the payment is
contingent on an event. For a $100 put option the payment is only made if the price of the underlying asset
drops below $100. A CDS payment only occurs if the price drops below par. A CDS differs from and option
in that the payment is triggered only by a price drop resulting from a defined credit event.
9. The focus in an asset-backed securities CDS (ABS CDS) is on the cash-paying ability of the collateral
and not on bankruptcy. Why?
CDS are written on asset-backed securities (ABS) and referred to as ABS CDS. Asset Backed Securities are
backed by a wide range of asset types.
In June 2005, the ISDA released what it refers to as its pay-as-you-go (PAUG) template for ABS CDS
focusing on cash flow adequacy of the ABS structure rather than the potential for bankruptcy. The ISDA
PAUG template provided the following three credit events that focus on cash flow adequacy for ABS
transactions:
(1) Failure to pay. The underlying reference obligation fails to make a scheduled interest or principal
payment.
(2) Writedown. The principal component of the underlying reference obligation is written down and deemed
irrecoverable.
(3) Distressed ratings downgrade. The underlying reference obligation is downgraded to
a rating of Caa2/CCC or lower
As can be seen, unlike a CDS where the reference entity is a corporation where a credit event is intended to
capture an event of default, the PAUG template seeks to capture any non-default events that impact the cash
flow of the specific reference ABS tranche.
10. Answer the below questions.
(a) For a single-name credit default swap, what is the difference between physical settlement and cash
settlement?
Credit default swaps can be either cash settled or physically settled.
 Physical delivery means that if a credit event occurs, the protection buyer delivers the reference
obligation to the protection seller and receives a cash payment equal to par.
 In a cash settlement the protection seller pays the protection buyer the difference between par and the
after-event price of the bond. The after-event price is determined by an auction (also called a “credit-
fixing event) conducted by the ISDA through the interdealer bond market.
For physical delivery, there is no need to determine an after-even price for the CDS to be settled, but the
auction price must be determined for cash CDS to be settled.
(b) In physical settlement, why is there a cheapest-to-deliver issue?
The market practice for settlement for single-name credit default swaps is physical settlement as opposed
to cash settlement. With physical settlement the protection buyer delivers a specified amount of the face
value of bonds of the reference entity to the protection seller.

4. 4
For a physical settled single-name CDS written on a reference entity (a company, municipality or
country) and not on a specific reference obligation (a specific bond issued by a company, municipality or
country), the protection buyer is granted, by custom, the choice of debt instrument issued by the reference
entity to deliver to satisfy the CDS. The ISDA swap documentation will set forth the characteristics
necessary for an issue to qualify as a deliverable obligation.
The protection seller pays the protection buyer the face value of the bonds. Since all reference entities that
are the subject of credit default swaps have many issues outstanding, there will be a number of alternative
issues of the reference entity that the protection buyer can deliver to the protection seller. These issues are
known as deliverable obligations.
The cheapest-to-deliver bond is determined from set of deliverable bonds through the auction process.
17. In an April 21, 2011 article in Bloomberg.com by Abigail Moses entitled, “Greece, Portugal Sovereign
Credit-Default Swaps Jump to Records,” the following statement appears:
“Credit-default swaps on Greece jumped 40 basis points to 1,340 basis points according to CMA,
signaling a 68 percent chance of default within five years.”
How is the “68 percent chance of default” obtained?
The “68 percent chance of default” can be obtained from relations that back out default probabilities from the
observed CDS spread. We begin with the equation:
Spread (in bps) = (1 – R) x q
q = default probability q.
For a CDS, this is not necessarily bankruptcy but the probability of a credit event.
R = the value of the reference security after a credit event.
Given an assumed recovery rate (R) and a Spread, the implied default probability equals:
q = Spread/(1 – R)
So, for example, if the observed 5-year CDS spread is 1,340 bps and the assumed recovery rate is 80.29%,
then the implied default probability is 68% as shown below:
q = 1340/(1 – 0.8029) = 0.6800 = 68.00%
18. Answer the below questions.
(a) Explain how a single-name CDS can be used by a portfolio manager who wants to short a reference
entity.
If a portfolio manager expects that an issuer will have difficulties in the future and wants to take a position
based on that expectation, it will short the bond of that issuer. However, since corporate bonds are illiquid,
shorting bonds in the corporate bond market is difficult. The equivalent position can be obtained by
entering into a swap as the protection buyer.

5. 5
Credit derivatives (such as a single-name credit default swap) are used by bond portfolio managers in the
normal course of activities to more efficiently control the credit risk of a portfolio and to more efficiently
transact than by transacting in the cash market. For example, credit derivatives allow a mechanism for
portfolio managers to more efficiently short a credit-risky security than by shorting in the cash market,
which is oftentimes difficult to do. For traders and hedge fund managers, credit derivatives provide a
means for leveraging an exposure in the credit market.
For a portfolio manager who engages in a single-name credit default swap, the manager can note that the
market practice for settlement is physical delivery. With physical settlement the protection buyer delivers a
specified amount of the face value of bonds of the reference entity to the protection seller. The protection
seller pays the protection buyer the face value of the bonds. Since all reference entities that are the subject
of credit default swaps have many issues outstanding, there will be a number of alternative issues of the
reference entity that the protection buyer can deliver to the protection seller. These issues are known as
deliverable obligations. The swap documentation will set forth the characteristics necessary for an issue to
qualify as a deliverable obligation. Just like for Treasury bond and note futures contracts, the short (in a
single-name credit default swap) has the choice of which issue to deliver that is specified as acceptable for
delivery. The short will select the cheapest-to-deliver issue, and the choice granted to the short is
effectively an embedded option. From the list of deliverable obligations, the protection buyer will select
for delivery to the protection seller the cheapest-to-deliver issue.
(b) Explain how a single-name CDS can be used by a portfolio manager who is having difficulty
acquiring the bonds of a particular corporation in the cash market.
If the portfolio manager desires a bond it is likely because of the cash flows (associated with the bond)
help the manager match assets and liabilities. While the “ideal” bond may be hard to find and purchase, a
single-name credit default swap can help realize the same desired cash flows. Thus, a single-name credit
default swap can be used by a portfolio manager who is having difficulty acquiring the bonds of a
particular corporation in the cash market. More details are given below.
The interdealer market has evolved to where single-name credit default swaps for corporate and sovereign
reference entities are standardized. While trades between dealers have been standardized, there are
occasional trades in the interdealer market where there is a customized agreement. For portfolio managers
seeking credit protection, dealers are willing to create customized products. The tenor, or length of time of
a credit default swap, is typically five years. Portfolio managers can have a dealer create a tenor equal to
the maturity of the reference obligation or have it constructed for a shorter time period to match the
manager’s investment horizon.
Exhibit 29-2 shows the mechanics of a single-name credit default swap. The cash flows are shown before
and after a credit event. It is assumed in the exhibit that there is physical settlement. Single-name credit
default swaps can be used in the following ways by portfolio managers:
o The liquidity of the swap market compared to the corporate bond market makes it more efficient to
obtain exposure to a reference entity by taking a position in the swap market rather than in the
cash market. To obtain exposure to a reference entity, a portfolio manager would sell protection
and thereby receive the swap premium.
o Conditions in the corporate bond market may be such that it is difficult for a portfolio manager to
sell the current holding of a corporate bond of an issuer for which he has a credit concern. Rather
than selling the current holding, the portfolio can buy protection in the swap market.
o If a portfolio manager expects that an issuer will have difficulties in the future and wants to take a

6. 6
position based on that expectation, it will short the bond of that issuer. However, shorting bonds in
the corporate bond market is difficult. The equivalent position can be obtained by entering into a
swap as the protection buyer.
o For a portfolio manager seeking a leveraged position in a corporate bond, this can be done in the
swap market. The economic position of a protection buyer is equivalent to a leveraged position in
a corporate bond.
19. How are index CDS used by portfolio managers?
A credit default index swap (CDX) provides credit exposure to a diversified basket of credits (bonds). They
can be used to create a synthetic short position in bonds (buying protection) or a synthetic long position in
bonds (selling protection) alter the portfolio managers credit risk.
Extra Questions:
1. How is a CDS like a standby letter of credit issued by a bank to the bond issuer or like bond insurance?
How is it different?
CDS shift credit exposure from the issuer of the bond to a credit protection seller. They are used to hedge the
credit exposure incurred by the holder of the bond, the buyer of the CDS.
A standby letter of credit issued by a bank to the issuer of the bond states that if the issuer fails to pay, the
bank will pay. Bond insurance works similarly - if the issuer fails to pay, the insurance company will pay.
In these ways, they are similar to a CDS in that the holder of the bond is paid (by the bank or bond insurance
company) if the issuer fails to pay.
A standby letter of credit or bond insurance differ from a CDS in that the issuer pays for the credit protection
and holder receives these protections when buying the bond. So the insurance is “included” with every bond.
In other words, you cannot buy the bond without the insurance and the insurance cannot be bought without
the bond.
In a credit default swap, the protection buyer pays a fee to the protection seller in return for the right to
receive a payment conditional upon the occurrence of a credit event by the reference obligation or the
reference entity. If a credit event occurs, the protection seller must make a payment. This is different from a
standby letter of credit or bond insurance in that you can buy the bond without protection or protection can be
bought without the bond.
2. What is the (approximate) relationship between the spread on a single name CDS (S), the probability of
default (q) and the recovery rate (R) if there is a default?
In any year, the probability of a default (q) multiplied by what you get paid if there is a default (1 –R) must
equal what you pay for the protection for that period (else there is an arbitrage opportunity).
In other words:
The Protection Spread (S) equals the Probability of Default (q) times the Amount Recovered if there is a
Default (1 – R).
S = q × (1 – R)

7. 7
Let S = 50 bps and R = 50%.
Probability of Default = q = S/(1 – R) = 0.005/(1 – 0.50) = 1.00%
Note that this is just an approximation of the relationship.
3. Assume the recovery rate equals 40% (a standard industry estimate). Estimate the annual cost of credit
protection if there is a 0.50%, 1.00%, 2.00% and 5.00% chance of default in any year.
q = 0.50% = 0.005
R = 40%
S = q × (1 – R) = 0.005(1 – 0.4) = 0.0030 or 30 bps
q = 1.00% = 0.010
R = 40%
S = q × (1 – R) = 0.010(1 – 0.4) = 0.0060 or 60 bps
q = 2.00% = 0.020
R = 40%
S = q × (1 – R) = 0.020(1 – 0.4) = 0.0120 or 120 bps
q = 5.00% = 0.050
R = 40%
S = q × (1 – R) = 0.050(1 – 0.4) = 0.0300 or 300 bps
4. Assume the recovery rate equals 40% (a standard industry estimate). Estimate the chance of default in
any year ANNUAL cost of credit protection is 100 bps, 200 bps and 500 bps.
S = 100 bps
R = 40%
q = S/(1 – R) = 0.0100/(1 – 0.4) = 0.0167 or 1.67% probability of default
S = 200 bps
R = 40%
q = S/(1 – R) = 0.0200/(1 – 0.4) = 0.0333 or 3.33% probability of default
S = 500 bps
R = 40%
q = S/(1 – R) = 0.0500/(1 – 0.4) = 0.0833 or 8.33% probability of default
5. Describe the SNAC rules for CDS payments. What is the benefit of these payment conventions to the
CDS market?
Starting in 2009, CDS contracts follow the Standard North American Corporate CDS (SNAC CDS) 100 bps
coupon or 500 bps coupon rules. All CDS quarterly payments are made on the same dates (3/20, 6/20, 9/20
and 12/20) and the amounts are computed using coupons of either 100 bps or 500 bps.
The quarterly payments are:
Quarterly CDS payment = Notional × 0.0100 × Actual/360
or
Quarterly CDS payment = Notional × 0.0500 × Actual/360

8. 8
What if the reference entity only requires a spread of 90 bps? Since you are required to pay 100 bps (and
therefore you are required to overpay by 100 – 90 = 10 bps), you will receive an upfront payment equal to the
expected present value of the amount you are required to overpay. (See the next question for the computation
of this upfront payment.
What if the reference entity requires a spread of 120 bps? Since you are required to pay 100 bps (and
therefore you are able to underpay by 120 – 100 = 10 bps), you will pay an upfront payment equal to the
expected present value of the amount you are required to underpay.
This is beneficial because all CDS contracts, regardless of the day they are initiated or the spread at the time
of initiation will have the same quarterly CDS payments made on the same days. The only difference will be
the upfront payments.
6. Assume the spread for a 5 year single name CDS is 90 bps. The recovery rate for the reference entity is
82%. The probability of default in any year is 5% and probability of default in any quarter is 5%/4 =
1.25%. It is initiated on 12/20/2013 and the contract follows the Standard North American Corporate
CDS (SNAC CDS) 100 bps coupon rules. Compute the upfront and periodic payments for the CDS.
In 2009, the ISDA and the CDS market started using Standard North American Corporate CDS contracts
(SNAC CDS contracts). These contracts all have fixed spreads (called coupons) of either 100 or 500 bps and
fixed quarterly payment dates of March, June, Sept and Dec 20th
.
So ALL single-name CDS contracts have one of two different terms:
Payments are on March, June, Sept and Dec 20th
and the payments are either 100 bps or 500 bps.
The payments are:
100 bps quarterly CDS payment = Notional × 0.0100 × Actual Days in Quarter/360
500 bps quarterly CDS payment = Notional × 0.0500 × Actual Days in Quarter/360
Note since the rule is Actual/360 and there are 365 or 366 days in a year, the fraction of the annual payment
paid each quarter will be at a minimum 25% and as much as 25.65%. The annual amount will be greater than
101.39% except in leap years when it will be 101.67% of the quoted CDS spread:
Start Date End Date
Days per
Quarter
Days per
Year Actual/360
Total
Annual
Percentage
12/20/2013 3/20/2014 90 0.2500
3/20/2014 6/20/2014 92 0.2556
6/20/2014 9/20/2014 92 0.2556
9/20/2014 12/20/2014 91 365 0.2528 1.0139
12/20/2014 3/20/2015 90 0.2500
3/20/2015 6/20/2015 92 0.2556
6/20/2015 9/20/2015 92 0.2556
9/20/2015 12/20/2015 91 365 0.2528 1.0139
12/20/2015 3/20/2016 91 0.2528
3/20/2016 6/20/2016 92 0.2556
6/20/2016 9/20/2016 92 0.2556
9/20/2016 12/20/2016 91 366 0.2528 1.0167

9. 9
What if, given the default risk and recovery rate of the reference entity, you should only be paying 90 bps but
are forced by the SNAC standardized contract to pay 100 bps?
Then you receive a cash payment at the initiation of the contract for the present value of each of the 100 – 90
= 10 bps overpayments.
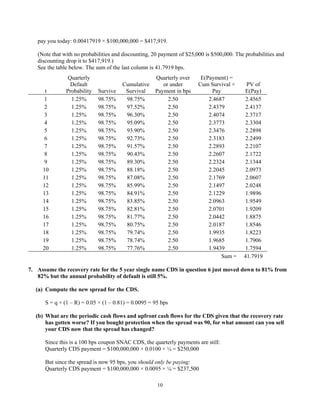
Consider a 5 year CDS on $100,000,000 notional amount initiated on December 20, 2013.
There are 4 x 5 = 20 quarterly payments. Each payment is approximately equal to (ignoring the Actual/360
rule and just multiplying by ¼):
Quarterly CDS payment = $100,000,000 × 0.0100 × ¼ = $250,000
But since the spread is 90 bps, you should only be paying:
Quarterly CDS payment = $100,000,000 × 0.0090 × ¼ = $225,000
So the standardized contract requires you to overpay $250,000 - $225,000 = $25,000 per quarter for 20
quarters.
Therefore, you will receive at the initiation of the contract, the present value of 20 quarterly payments of
$25,000 discounted at LIBOR (assume LIBOR 2.00% APR so 0.50% per quarter).
But it’s not so simple. There is a chance (if the reference entity defaults) that you will not have to make the
next payment of 100 bps (and therefore NOT pay the extra 10 bps x $100,000,000 x ¼ = $25,000).
So how likely is it that the CDS will still be in force when a payment time comes?
Consider the first year (4 payments) and assume the default probability is 5% is any year to .05/4 = 1.25%
quarter.
 There is a 100% - 1.25% = 98.75% chance of making it to the first payment.
 There is a (0.9875)2
= 97.52% chance of making it to the second payment.
 There is a (0.9875)3
= 96.30% chance of making it to the third payment.
 There is a (0.9875)4
= 95.09% chance of making it to the fourth payment.
Let: qP = probability of default in any period = q/4 = 5%/4 = 1.25%
(1 – qP) = probability of not default in any period = 98.75%
Qt = (1 – qP)t
= Prob of making it to time t (and therefore making the CDS payment) = 0.9875t
r = periodic LIBOR = 2.00%/4 = 0.50%
The expected excess payment in any period = Qt × (100 – 90)/4 = Qt × 2.50
The PV of that excess payment = Qt × 2.50/(1 + r)t
The present value of all the excess payments you have to make over the life of the swap given that you are
forced by the SNAC CDS to pay 100 bps when you should only pay 90 is:
PV = Q1[(100 – 90)/4]/(1 + r) + Q2[(100 – 90)/4]/(1 + r)2
+ … + Q20[(100 – 90)/4]/(1 + r)20
= 0.9875 x 2.50/(1.0050) + .9752 x 2.50/(1.0050)2
+ … + 0.7776[(100 – 90)/4]/(1.0050)20
= 41.7919 bps
So on $100,000,000 notional amount with a spread of 90 bps, but 100 BPS SNAC coupon,
You would make quarterly payments of 0.0100/4 × $100,000,000 = $250,000 to the protection seller.
But since you should only be making payments of $225,000 to the protection seller, the protection seller will

10. 10
pay you today: 0.00417919 × $100,000,000 = $417,919.
(Note that with no probabilities and discounting, 20 payment of $25,000 is $500,000. The probabilities and
discounting drop it to $417,919.)
See the table below. The sum of the last column is 41.7919 bps.
t
Quarterly
Default
Probability Survive
Cumulative
Survival
Quarterly over
or under
Payment in bps
E(Payment) =
Cum Survival ×
Pay
PV of
E(Pay)
1 1.25% 98.75% 98.75% 2.50 2.4687 2.4565
2 1.25% 98.75% 97.52% 2.50 2.4379 2.4137
3 1.25% 98.75% 96.30% 2.50 2.4074 2.3717
4 1.25% 98.75% 95.09% 2.50 2.3773 2.3304
5 1.25% 98.75% 93.90% 2.50 2.3476 2.2898
6 1.25% 98.75% 92.73% 2.50 2.3183 2.2499
7 1.25% 98.75% 91.57% 2.50 2.2893 2.2107
8 1.25% 98.75% 90.43% 2.50 2.2607 2.1722
9 1.25% 98.75% 89.30% 2.50 2.2324 2.1344
10 1.25% 98.75% 88.18% 2.50 2.2045 2.0973
11 1.25% 98.75% 87.08% 2.50 2.1769 2.0607
12 1.25% 98.75% 85.99% 2.50 2.1497 2.0248
13 1.25% 98.75% 84.91% 2.50 2.1229 1.9896
14 1.25% 98.75% 83.85% 2.50 2.0963 1.9549
15 1.25% 98.75% 82.81% 2.50 2.0701 1.9209
16 1.25% 98.75% 81.77% 2.50 2.0442 1.8875
17 1.25% 98.75% 80.75% 2.50 2.0187 1.8546
18 1.25% 98.75% 79.74% 2.50 1.9935 1.8223
19 1.25% 98.75% 78.74% 2.50 1.9685 1.7906
20 1.25% 98.75% 77.76% 2.50 1.9439 1.7594
Sum = 41.7919
7. Assume the recovery rate for the 5 year single name CDS in question 6 just moved down to 81% from
82% but the annual probability of default is still 5%.
(a) Compute the new spread for the CDS.
S = q × (1 – R) = 0.05 × (1 – 0.81) = 0.0095 = 95 bps
(b) What are the periodic cash flows and upfront cash flows for the CDS given that the recovery rate
has gotten worse? If you bought protection when the spread was 90, for what amount can you sell
your CDS now that the spread has changed?
Since this is a 100 bps coupon SNAC CDS, the quarterly payments are still:
Quarterly CDS payment = $100,000,000 × 0.0100 × ¼ = $250,000
But since the spread is now 95 bps, you should only be paying:
Quarterly CDS payment = $100,000,000 × 0.0095 × ¼ = $237,500

11. 11
So the standardized contract requires you to overpay $250,000 - $237,500 = $12,500 per quarter for 20
quarters.
Therefore, a purchaser of the CDS will receive at the time of purchase, the present value of the expected
value of 20 quarterly payments of $12,500 discounted at LIBOR (assume LIBOR 2.00% APR so 0.50%
per quarter).
So the payments for a CDS on this entity have gone from an excess of 2.50 bps on $100,000,000 =
$25,000 to an excess 1.25 bps on $100,000,000 = $12,500
The probability of having to make each of these payments has not changed, only the amount, and therefore
the expected payment and the PV of the expected payment. So the upfront payment for someone buying
the CDS is 20.8959 bps on $100,000,000 or $208,959.
See the table below.
t
Quarterly
Default
Probability Survive
Cumulative
Survival
Quarterly over
or under
Payment in bps
E(Payment) =
Cum Survival ×
Pay
PV of
E(Pay)
1 1.25% 98.75% 98.75% 1.25 1.2344 1.2282
2 1.25% 98.75% 97.52% 1.25 1.2189 1.2068
3 1.25% 98.75% 96.30% 1.25 1.2037 1.1858
4 1.25% 98.75% 95.09% 1.25 1.1887 1.1652
5 1.25% 98.75% 93.90% 1.25 1.1738 1.1449
6 1.25% 98.75% 92.73% 1.25 1.1591 1.1250
7 1.25% 98.75% 91.57% 1.25 1.1446 1.1054
8 1.25% 98.75% 90.43% 1.25 1.1303 1.0861
9 1.25% 98.75% 89.30% 1.25 1.1162 1.0672
10 1.25% 98.75% 88.18% 1.25 1.1023 1.0486
11 1.25% 98.75% 87.08% 1.25 1.0885 1.0304
12 1.25% 98.75% 85.99% 1.25 1.0749 1.0124
13 1.25% 98.75% 84.91% 1.25 1.0614 0.9948
14 1.25% 98.75% 83.85% 1.25 1.0482 0.9775
15 1.25% 98.75% 82.81% 1.25 1.0351 0.9605
16 1.25% 98.75% 81.77% 1.25 1.0221 0.9437
17 1.25% 98.75% 80.75% 1.25 1.0093 0.9273
18 1.25% 98.75% 79.74% 1.25 0.9967 0.9111
19 1.25% 98.75% 78.74% 1.25 0.9843 0.8953
20 1.25% 98.75% 77.76% 1.25 0.9720 0.8797
Sum = 20.8959
(c) Is buying CDS protection similar to going long or going short a bond?
Did the bond’s outlook improve or deteriorate when the spread went from 90 to 95?
Did you make or lose money when the spread went from 90 to 95? Explain.
Buying a CDS is like going short a bond. The bond’s outlook deteriorated.
You bought protection when the issuer was “safer” and sold protections when the issuer was less safe.

12. 12
Given the SNAC CDS, you are required to pay $250,000 per quarter on the CDS you bought and get
$250,000 per quarter on the CDS you sold – so you are flat quarterly payments.
You “bought protection” when the recovery rate was 82%. The spread was 90 bps, so you were over
paying by 10 bps and so you collected $417,919 since you committed to overpay by 10 bps for the next 5
years.
When the recovery rate decreased to 81% (the bond got worse), the spread moved to 95 bps – protection
now costs more. This is the point in time that you agreed to “sell protection” to off-set your CDS position.
So you agreed to receive 5 bps per year more than you should receive (you get 100 and should only get
95). Therefore you would have to pay $208,959 upfront to whomever has agreed to overpay 5 bps per year
for protection.
So you collected $417,919 when you bought protection. At that point the recovery rate was 82% and the
spread was 90 bps.
You paid $208,959 when you sold protection to go flat. At that point, the recovery rate was 81% and the
spread was 95 bps.
Your profit from taking a “short” derivative position on the bond is $417,919 – $208,959 = $208,960.
8. Assume the recovery rate for a non-investment grade reference entity is 25% and the annual
probability of default is 8.00%. A CDS with $1,000,000 notional value is initiated on 12/20/2013 and the
contract follows the Standard North American Corporate CDS (SNAC CDS) 500 bps coupon rules.
(a) Compute the annual spread for the CDS.
S = q × (1 – R) = 0.08 × (1 – 0.25) = 0.0600 = 600 bps
(b) Compute the periodic cash flows and upfront cash flows for the CDS.
Since this is a 500 bps coupon SNAC CDS, the quarterly payments are:
Quarterly CDS payment = $1,000,000 × 0.0500 × ¼ = $12,500
But since the spread is 600 bps, you should be paying:
Quarterly CDS payment = $1,000,000 × 0.0600 × ¼ = $15,000
So the standard contract requires you to underpay $15,000 - $12,500 = $2,500 per quarter for 20 quarters.
Therefore, a purchaser of the CDS must pay at the time of purchase, the present value of the expected
value 20 quarterly payments of $2,500 discounted at LIBOR (0.50% per quarter).
The PV of the expected value is -387.8573 bps. On $1,000,000 notional value, the upfront payment you
must make as the purchaser of this CDS is $38,786.
See the table below. Note the sum of the last column is -387.8573 bps.

13. 13
t
Quarterly
Default
Probability Survive
Cumulative
Survival
Quarterly over
or under
Payment in bps
E(Payment) =
Cum Survival ×
Pay
PV of
E(Pay)
1 2.00% 98.00% 98.00% -25.00 -24.5000 -24.3781
2 2.00% 98.00% 96.04% -25.00 -24.0100 -23.7717
3 2.00% 98.00% 94.12% -25.00 -23.5298 -23.1804
4 2.00% 98.00% 92.24% -25.00 -23.0592 -22.6037
5 2.00% 98.00% 90.39% -25.00 -22.5980 -22.0414
6 2.00% 98.00% 88.58% -25.00 -22.1461 -21.4932
7 2.00% 98.00% 86.81% -25.00 -21.7031 -20.9585
8 2.00% 98.00% 85.08% -25.00 -21.2691 -20.4371
9 2.00% 98.00% 83.37% -25.00 -20.8437 -19.9288
10 2.00% 98.00% 81.71% -25.00 -20.4268 -19.4330
11 2.00% 98.00% 80.07% -25.00 -20.0183 -18.9496
12 2.00% 98.00% 78.47% -25.00 -19.6179 -18.4782
13 2.00% 98.00% 76.90% -25.00 -19.2256 -18.0186
14 2.00% 98.00% 75.36% -25.00 -18.8410 -17.5703
15 2.00% 98.00% 73.86% -25.00 -18.4642 -17.1333
16 2.00% 98.00% 72.38% -25.00 -18.0949 -16.7071
17 2.00% 98.00% 70.93% -25.00 -17.7330 -16.2915
18 2.00% 98.00% 69.51% -25.00 -17.3784 -15.8862
19 2.00% 98.00% 68.12% -25.00 -17.0308 -15.4910
20 2.00% 98.00% 66.76% -25.00 -16.6902 -15.1057
Sum = -387.8573
(c) Now assume the annual probability of default increases from 8% to 10%. Compute the CDS
spread, the periodic cash flows and the upfront cash flows for the CDS. What is the net upfront
payments if you wish to sell the CDS?
S = q × (1 – R) = 0.10 × (1 – 0.25) = 0.0750 = 750 bps
Since this is a 500 bps coupon SNAC CDS, the quarterly payments are still:
Quarterly CDS payment = $1,000,000 × 0.0500 × ¼ = $12,500
But since the spread is now 750 bps, you should be paying:
Quarterly CDS payment = $1,000,000 × 0.0750 × ¼ = $18,750
So the standardized contract requires the purchaser to underpay $18,750 - $12,500 = $6,250 per quarter for
20 quarters.
Therefore, a purchaser of the CDS will pay at the time of purchase, the present value of the expected value
20 quarterly payments of $6,250 discounted at LIBOR (0.50% per quarter).
The PV of the expected value is -923.2635 bps. On $1,000,000 notional value, the upfront payment you
will receive as the seller of this CDS is $92,326.

14. 14
T
Quarterly
Default
Probability Survive
Cumulative
Survival
Quarterly over
or under
Payment in bps
E(Payment) =
Cum Survival ×
Pay
PV of
E(Pay)
1 2.50% 97.50% 97.50% -62.50 -60.9375 -60.6343
2 2.50% 97.50% 95.06% -62.50 -59.4141 -58.8243
3 2.50% 97.50% 92.69% -62.50 -57.9287 -57.0684
4 2.50% 97.50% 90.37% -62.50 -56.4805 -55.3649
5 2.50% 97.50% 88.11% -62.50 -55.0685 -53.7122
6 2.50% 97.50% 85.91% -62.50 -53.6918 -52.1088
7 2.50% 97.50% 83.76% -62.50 -52.3495 -50.5533
8 2.50% 97.50% 81.67% -62.50 -51.0407 -49.0443
9 2.50% 97.50% 79.62% -62.50 -49.7647 -47.5803
10 2.50% 97.50% 77.63% -62.50 -48.5206 -46.1600
11 2.50% 97.50% 75.69% -62.50 -47.3076 -44.7821
12 2.50% 97.50% 73.80% -62.50 -46.1249 -43.4453
13 2.50% 97.50% 71.95% -62.50 -44.9718 -42.1484
14 2.50% 97.50% 70.16% -62.50 -43.8475 -40.8903
15 2.50% 97.50% 68.40% -62.50 -42.7513 -39.6696
16 2.50% 97.50% 66.69% -62.50 -41.6825 -38.4855
17 2.50% 97.50% 65.02% -62.50 -40.6404 -37.3367
18 2.50% 97.50% 63.40% -62.50 -39.6244 -36.2221
19 2.50% 97.50% 61.81% -62.50 -38.6338 -35.1409
20 2.50% 97.50% 60.27% -62.50 -37.6680 -34.0919
Sum = -923.2635
Your net is -$38,786 + 92,326 = $53,541.
Note you were long the CDS (similar to short the bond) and the bond got worse so you made money.
You “bought protection” when the default rate was 8%. The spread was 600 bps, so you were underpaying
paying by 100 bps and so you paid $38,786 since you committed to underpay by 100 bps for the next 5
years.
When the default rate increased to 10% (the bond got worse), the spread moved to 750 bps – protection
now costs more.
At the point you agreed to “sell protection” to off-set your CDS position. So you agreed to receive 250 bps
per year less than you should receive (you get 500 and should get 750). Therefore you would be paid
$92,326 upfront to whomever has agreed to underpay 250 bps per year for protection.
So you paid $38,786 when you bought protection. At that point the default probability was 8% and the
spread was 600 bps.
You received $92,326 when you sold protection to go flat. At that point, the default probability was 10%
and the spread was 750 bps.
Your profit from taking a “short” derivative position on the bond is -$38,786 + 92,326 = $53,541.

15. 15
(d) Now assume the annual probability of default decreases from 8% to 6%. Compute the CDS spread,
the periodic cash flows and the upfront cash flows for the CDS. What is the net upfront payments if
you wish to sell the CDS?
S = q × (1 – R) = 0.06 × (1 – 0.25) = 0.0450 = 450 bps
Since this is a 500 bps coupon SNAC CDS, the quarterly payments are still:
Quarterly CDS payment = $1,000,000 × 0.0500 × ¼ = $12,500
But since the spread is now 450 bps, you should be paying:
Quarterly CDS payment = $1,000,000 × 0.0450 × ¼ = $11,250
So the standardized contract requires the purchaser to OVERPAY $12,500 - $11,250 = $1,250 per quarter
for 20 quarters. Therefore, a purchaser of the CDS will get at the time of purchase, the present value of the
expected value 20 quarterly payments of $1,250 discounted at LIBOR (0.50% per quarter).
The PV of the expected value is 203.7934 bps. On $1,000,000 notional value, the upfront payment you
will pay as the seller of this CDS is $20,379. Your net is -$38,786 + -20,379 = -$59,165
t
Quarterly
Default
Probability Survive
Cumulative
Survival
Quarterly over
or under
Payment in bps
E(Payment) =
Cum Survival ×
Pay
PV of
E(Pay)
1 1.50% 98.50% 98.50% 12.50 12.3125 12.2512
2 1.50% 98.50% 97.02% 12.50 12.1278 12.0074
3 1.50% 98.50% 95.57% 12.50 11.9459 11.7685
4 1.50% 98.50% 94.13% 12.50 11.7667 11.5343
5 1.50% 98.50% 92.72% 12.50 11.5902 11.3047
6 1.50% 98.50% 91.33% 12.50 11.4164 11.0798
7 1.50% 98.50% 89.96% 12.50 11.2451 10.8593
8 1.50% 98.50% 88.61% 12.50 11.0764 10.6432
9 1.50% 98.50% 87.28% 12.50 10.9103 10.4314
10 1.50% 98.50% 85.97% 12.50 10.7466 10.2238
11 1.50% 98.50% 84.68% 12.50 10.5854 10.0203
12 1.50% 98.50% 83.41% 12.50 10.4266 9.8209
13 1.50% 98.50% 82.16% 12.50 10.2702 9.6255
14 1.50% 98.50% 80.93% 12.50 10.1162 9.4339
15 1.50% 98.50% 79.72% 12.50 9.9645 9.2462
16 1.50% 98.50% 78.52% 12.50 9.8150 9.0622
17 1.50% 98.50% 77.34% 12.50 9.6678 8.8818
18 1.50% 98.50% 76.18% 12.50 9.5227 8.7051
19 1.50% 98.50% 75.04% 12.50 9.3799 8.5319
20 1.50% 98.50% 73.91% 12.50 9.2392 8.3621
Sum = 203.7934
Note you were long the CDS (similar to short the bond) and the bond got better so you lost money.

16. 16
9. A five year $10,000,000 notional value CDS on a bond with an 80% recovery rate and a 6.00%
probability of default has a 100 bps coupon and a spread of 120 bps. Therefore the upfront payment is
$81,517.
(a) If you buy protection using the CDS, do you get the upfront payment or pay the upfront payment?
If you buy the CDS, you should be paying 120/4 = 30 bps per quarter.
But you are actually paying 100/4 = 25 per quarter.
Since you are paying 5 bps on $10,000,000 = $5,000 less than you should each quarter, you pay the
upfront of $81,517
(b) If you sell protection using the CDS, do you get the upfront or pay the upfront?
If you sell the CDS, you should be getting 120/4 = 30 bps per quarter.
But you are actually getting 100/4 = 25 per quarter.
Since you are getting 5 bps on $10,000,000 = $5,000 less than you should each quarter, you get the upfront
of $81,517.
(c) Assume the default probability moves to 6.05% and so the spread moves from 120 to 121 and the
upfront payment moves to $85,487. Who made money, the buyer or seller of protection?
If you bought the CDS at 120 bps, then you paid $81,517 and would get $85,487 now from selling it. So
your profit is -$81,517 + $85,487 = $3,969.
(d) At 120 bps, what is the Spread PV01 for the CDS?
The Spread PV01 is the dollar value of 1 bp of spread.
It is $85,487 - $81,517 = $3,969
10. Describe the cash flows for an Index Credit Default Swap (CDX).
An Index Credit Default Swap (CDX) is the sum of many cash-settled individual CDS contracts. The seller of
the protection sells protection on an equally-weighted basket of reference entities. This basket is determined
(by agreement) by IHS Markit.
Markit was created in 2001 by a consortium of investment banks to act as an arms-length entity to price OTC
transactions of derivative securities. It merged with IHS in 2016.
Every six months (on 3/20 and 9/20) IHS Markit creates a new index of 125 Investment Grade bonds (CDX-
IG). A credit default swap on the CDX-IG will have a fixed coupon equal to 100 bps, just like a single name
CDS. The average of the CDS spreads of the 125 bonds in the index is the required spread for the CDX.
But just like a single name CDS, the quarterly payments are computed using a fixed spread (or running spread
or coupon rate) of 100 bps.
Quarterly CDX payment = Notional × 0.0100 × Actual/360
So given the actual spread for the 125 bonds, an upfront payment for the CDX is computed using the method
described above.

17. 17
If a credit event occurs for one of the 125 reference entities in the index, the protection seller pays the
protection buyer the difference between par and the after-event price of the reference security.
But unlike a single-name CDS, the CDX does not cease to exist. The one bond that had the event is removed
from the index and the CDX continues to exist on the rest of the 124 reference entities, but the notional
amount and quarterly payments are reduced by 1/125.
11. A protection buyer uses an Index Credit Default Swap (CDX) created on 12/20/2018 to buy protection
on $10,000,000 notional amount. The CDX has a coupon of 100 bps and a required spread of 100 bps.
(a) Compute the upfront payment on 12/20/2018.
Since the spread is equal to the coupon, there is no upfront payment.
(b) Compute the first four quarterly payments paid 3/20/2019, 6/20/2019, 9/20/2019 and 12/20/2019 for
the swap assuming no credit events. Also compute the total annual payments as a percentage of the
notional value. Is this total amount greater than or less than the coupon percentage? Explain.
Quarterly CDX payment = Notional × 0.0100 × Actual/360
Start Date End Date
Days per
Quarter
Days per
Year Actual/360
Total Annual
Percentage
12/20/2018 3/20/2019 90 0.2500
3/20/2019 6/20/2019 92 0.2556
6/20/2019 9/20/2019 92 0.2556
9/20/2019 12/20/2019 91 365 0.2528 1.0139
Quarterly CDX payment on 3/20/2019 = $10,000,000 × 0.0100 × 90/360 = $25,000
Quarterly CDX payment on 6/20/2019 = $10,000,000 × 0.0100 × 92/360 = $25,556
Quarterly CDX payment on 9/20/2019 = $10,000,000 × 0.0100 × 92/360 = $25,556
Quarterly CDX payment on 12/20/2019 = $10,000,000 × 0.0100 × 91/360 = $25,278
$101,389
The total annual payments are $101,389 which is 1.01389% or 101.389 bps of the notional amount which
is greater than 100 bps.
The reason is that the payment convention assumes there are 360 days per year when there are actually
365 days per year, so the smallest quarterly payment is 0.25.
(c) Now assume one of the bonds in the index has a credit event immediately after the CDX is initiated
and the recovery price for the bond is 40%. Compute the cash flow for the credit event and the first
four quarterly payments paid 3/20/2019, 6/20/2019, 9/20/2019 and 12/20/2019 for the CDX.
After the credit event, the protection seller will pay the protection buyer for the bond that defaulted:
$10,000,000/125 × (1 – 0.40) = $48,000
The notional amount will now be $10,000,000 × 124/125 = $9,920,000

18. 18
Quarterly CDX payment on 3/20/2019 = $9,920,000 × 0.0100 × 90/360 = $24,800
Quarterly CDX payment on 6/20/2019 = $9,920,000 × 0.0100 × 92/360 = $25,351
Quarterly CDX payment on 9/20/2019 = $9,920,000 × 0.0100 × 92/360 = $25,351
Quarterly CDX payment on 12/20/2019 = $9,920,000 × 0.0100 × 91/360 = $25,076
$100,578
Note that $100,578/$9,920,000 = 101.389 bps
12. You wish to speculate on the general credit risk of high-yield bonds.
(a) Describe how you might do this using a five-year Index CDX if you wish to profit if the credit
worsens.
Every March 27 and Sept 27, IHS Markit produces an index of 100 high yield bonds (CDX-HY). The
CDX contracts trade with a coupon (also called the running spread) of 500 bps. Assume, given the default
probabilities and recovery rates of the bonds in the index, the require spread for the index is 420 bps.
If you wish to profit if credit worsens, then you buy protection (long a CDX is like short a bond). Since
you are required to pay 500 bps if you buy protection but the required spread is 420 bps, you will overpay
by 80 bps. You will collect the upfront payment of the present value of the expected value of those
overpayments. Assume the payment you receive on $1,000,000 notional value is $32,607.
Now assume the next day the credit worsens for the 100 bonds in the index and the new required average
spread for 100 bonds is 490. The new upfront payment you would have to pay to sell the protection is
$3,976.
Note that since the contract is standardized, the quarterly payments you agreed to make when you bought
the contract and the quarterly payments you agreed to receive when you sold the contract are the same so
the transactions cancel each other out.
The net is the difference in the upfront payments $32,607 - $3,976 = $28,631.