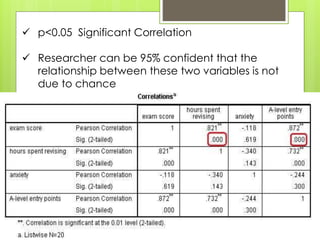
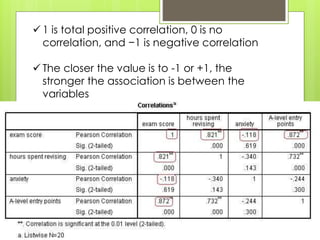
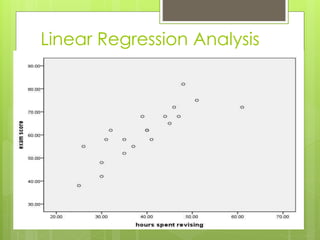
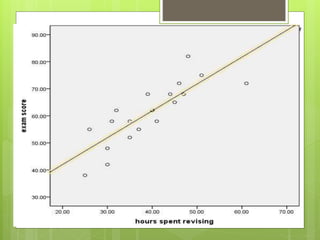
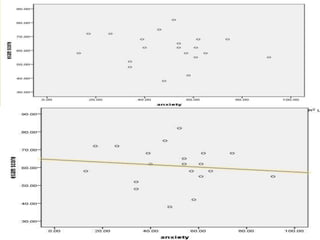
This document discusses various statistical analyses that can be used to analyze the relationship between variables: 1. Bivariate correlation measures the strength and direction of association between two variables using Pearson's correlation coefficient (r). A significant correlation is when p<0.05. 2. Linear regression analysis uses linear equations to model relationships between a dependent variable and one or more independent variables. It identifies outliers that do not follow patterns. 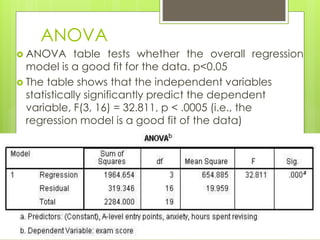3. Multiple regression extends linear regression to multiple independent variables, allowing analysis of their collective influence on a dependent variable. It provides measures like R and R-squared of the model's accuracy and fit.

1. NYC Charter
School
Performance on
the 2012-13 State
Exams
1.
Bivariate
Correlations
2.
Linear Regression
Analysis
3.
Multiple
Regression
Analysis

2. Bivariate Correlations
 Bivariate
Correlation
 Paersone
Correlation or Co-efficient of
correlation
 Scale
level of measurement

3.  p<0.05 Significant Correlation
 Researcher can be 95% confident that the
relationship between these two variables is not
due to chance

4.  Denoted
 -1
by r
≤ r ≤ +1

0 ------- ±0.3
No Relation

±0.3 ------- ±0.5
Weak Relation

±0.5 ------- ±0.8
Moderate Relation

±0.8 ------- ±1
Strong Relation

5.  1 is total positive correlation, 0 is no
correlation, and −1 is negative correlation
 The closer the value is to -1 or +1, the
stronger the association is between the
variables

6. Linear Regression Analysis

9. Outlier
 There should be no significant outliers. Outliers are simply
single data points within your data that do not follow the
usual pattern.
 The problem with outliers is that they can have a negative
effect on the regression equation that is used to predict the
value of the dependent (outcome) variable based on the
independent (predictor) variable.

10. Multiple Regression: Model Sum
a. R tells the reliability & mathematical relationship.
1. R Square (co-efficient of determination) tells the percentage of
accuracy.
2. Also percentage of variation that can not be controlled i.e.
3. (1-R Square)
i.
Adjusted R2, It can be negative & always less than or equal to R
ii. Adjusted R2 will be more useful only if the R2 is calculated based on
a sample, not the entire population
iii. Adjusted R2 increases only if the new term improves the model more
than would be expected by chance

11. ANOVA
 ANOVA
table tests whether the overall regression
model is a good fit for the data. p<0.05
 The table shows that the independent variables
statistically significantly predict the dependent
variable, F(3, 16) = 32.811, p < .0005 (i.e., the
regression model is a good fit of the data)

12. Coefficients
𝑦 = −11.823 + 0.551𝑥1 + 0.104𝑥2 + 1.989𝑥3
 How much the dependent variable varies with an
independent variable , when all other independent
variables are held constant.
 T value less than ±2 is not important
 Significant value of x
