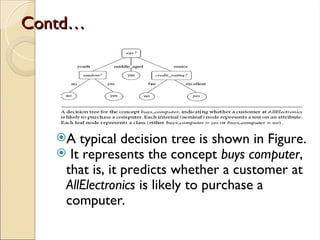
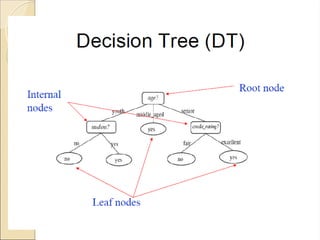
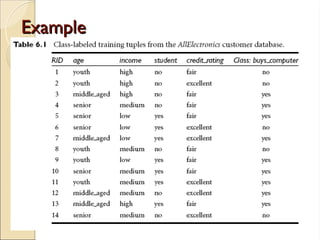
The document discusses decision tree induction, which involves creating a flowchart-like structure for classification tasks, where internal nodes test attributes and leaf nodes denote class labels. It highlights the process of selecting the best attribute for splitting training tuples using measures like information gain, gain ratio, and Gini index, with examples illustrating how to determine the splitting attribute. The final decision tree, based on attribute evaluation, predicts whether a customer is likely to purchase a computer.