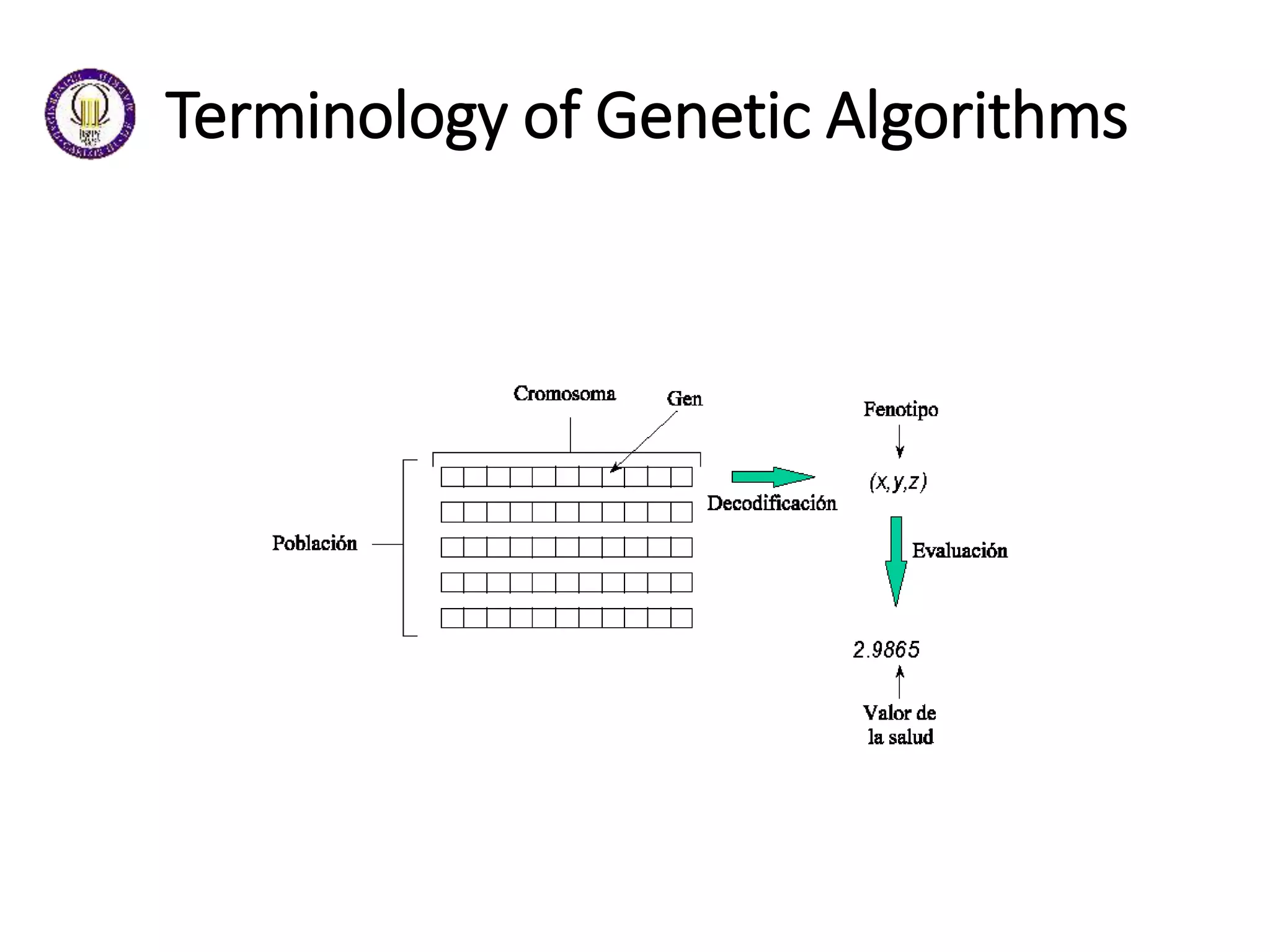
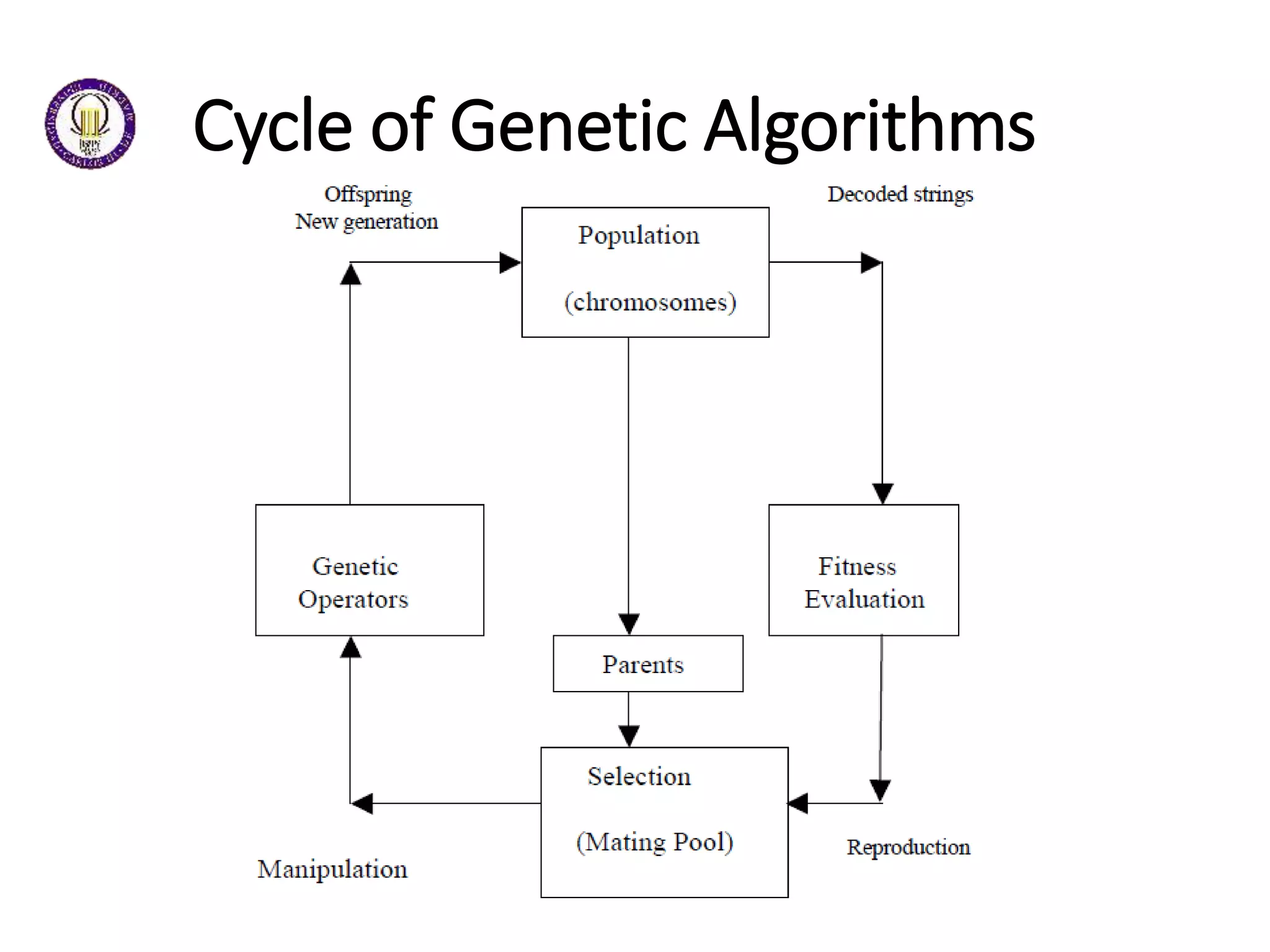
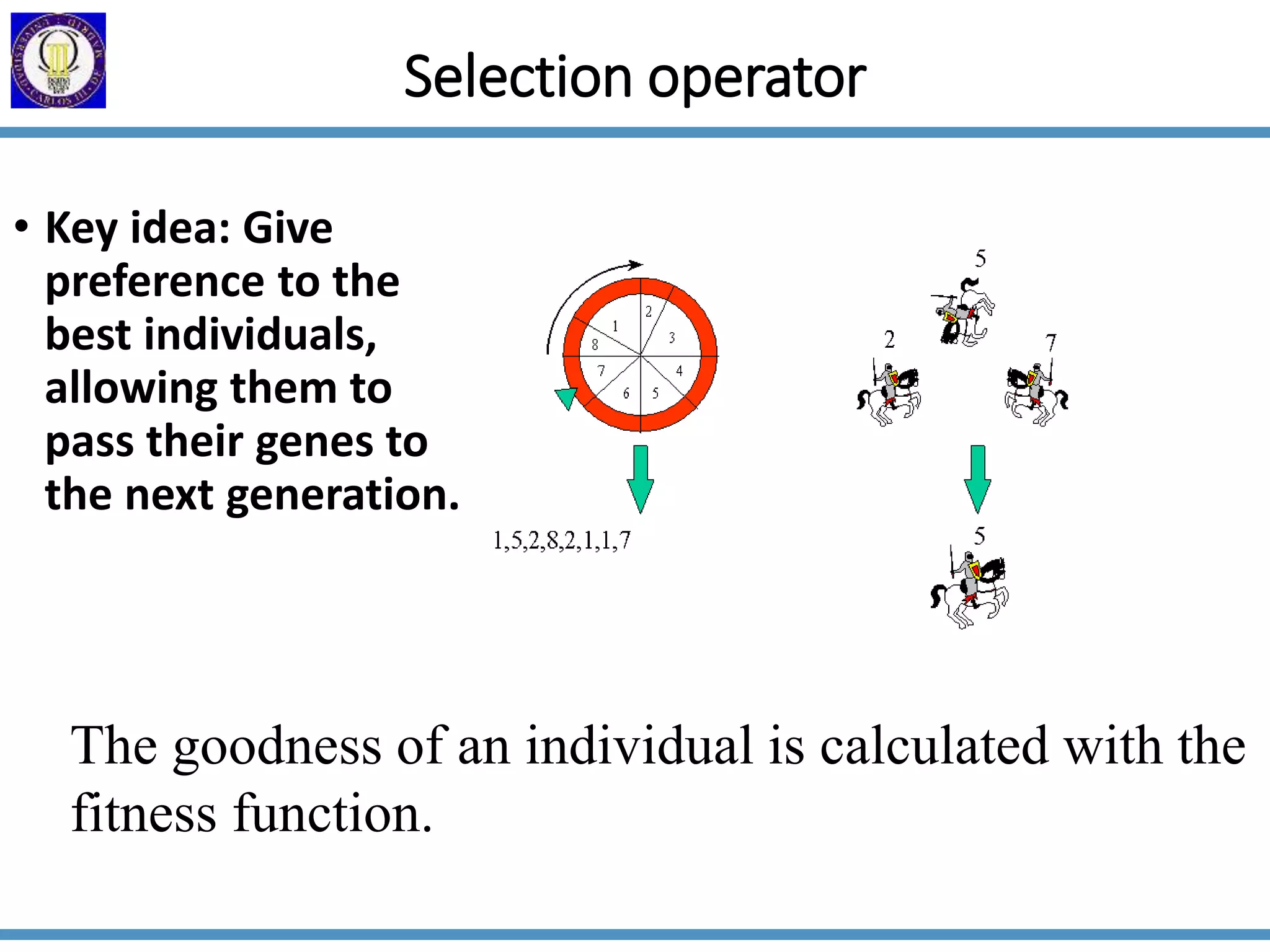
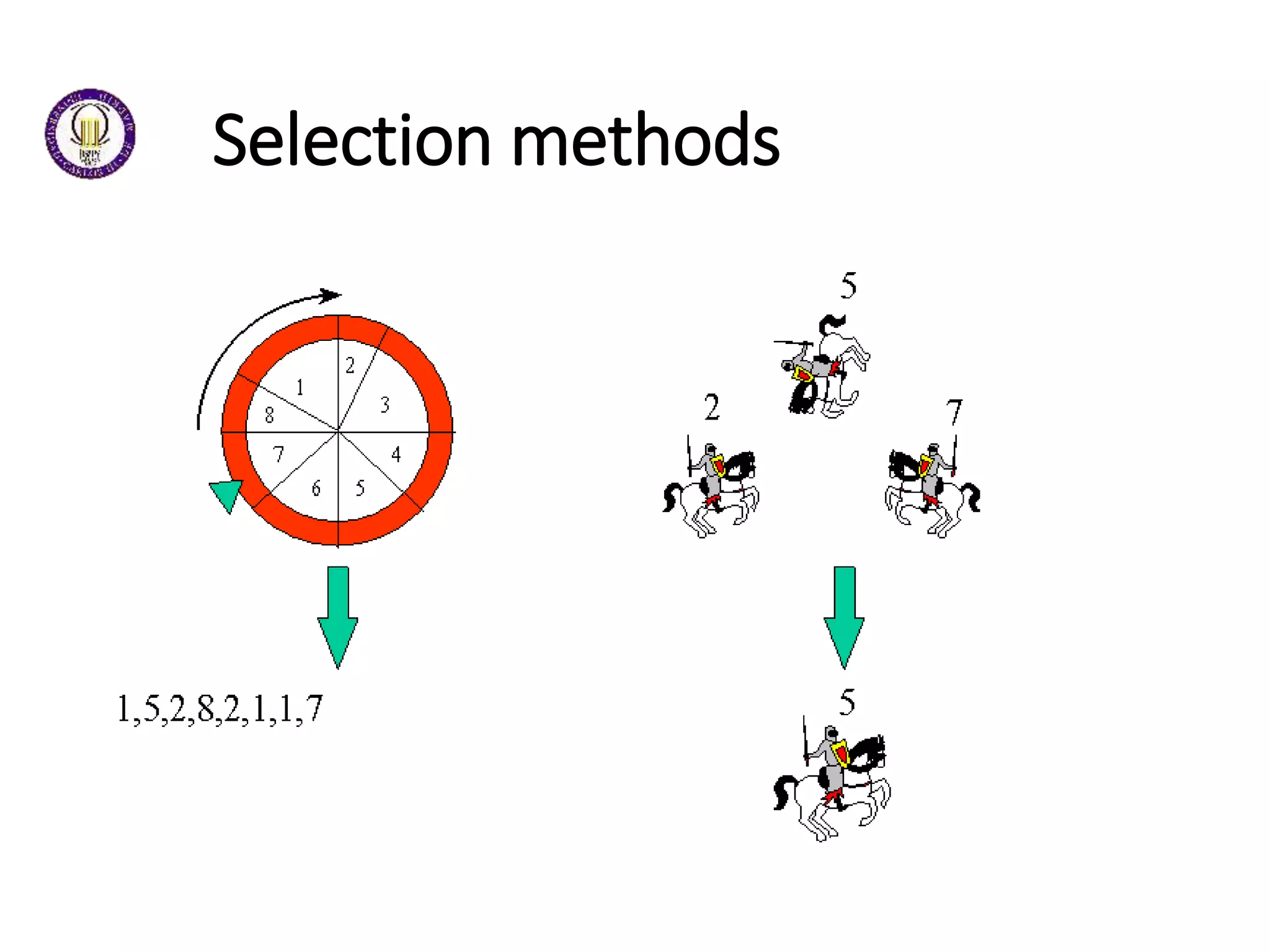
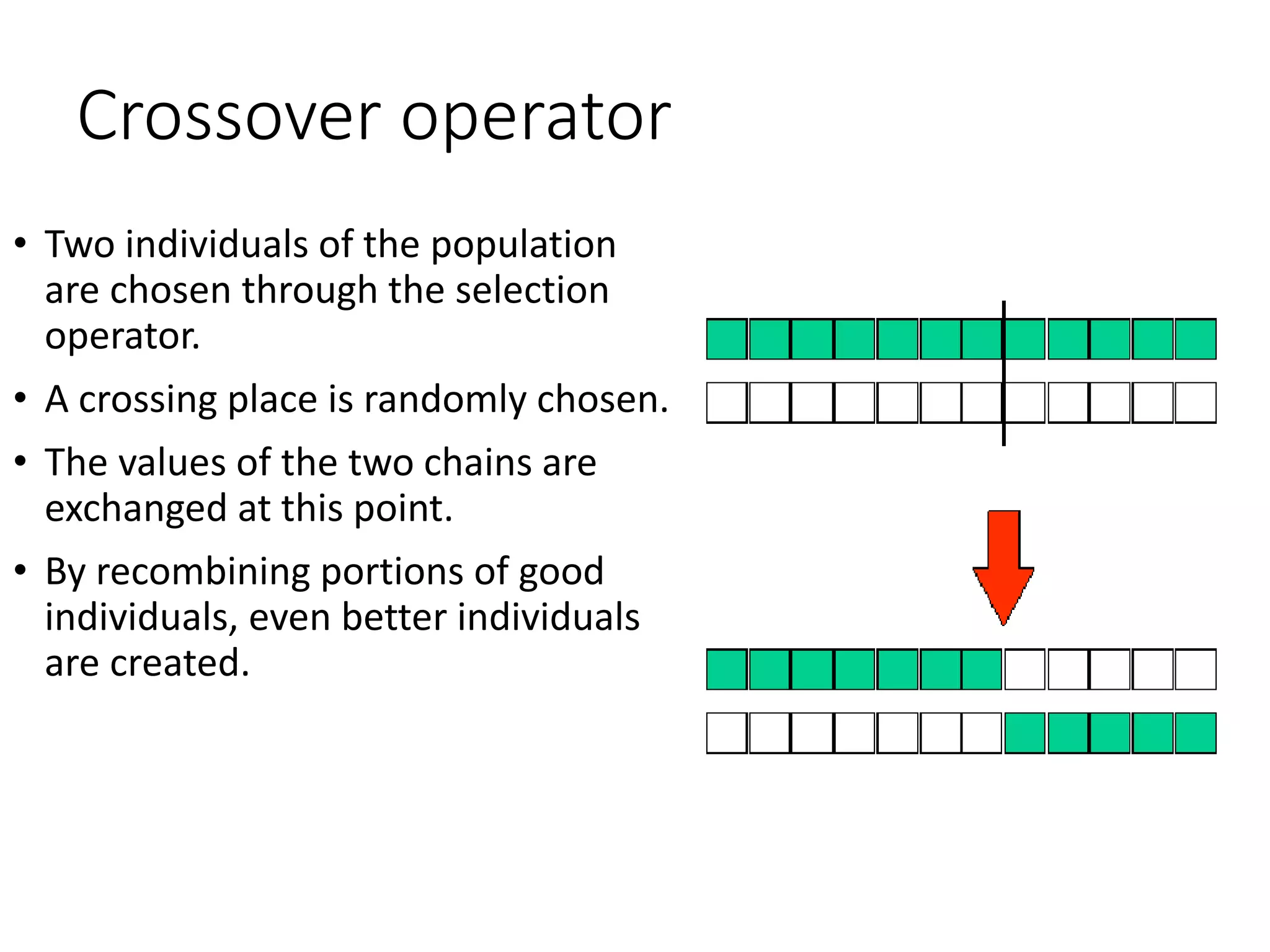
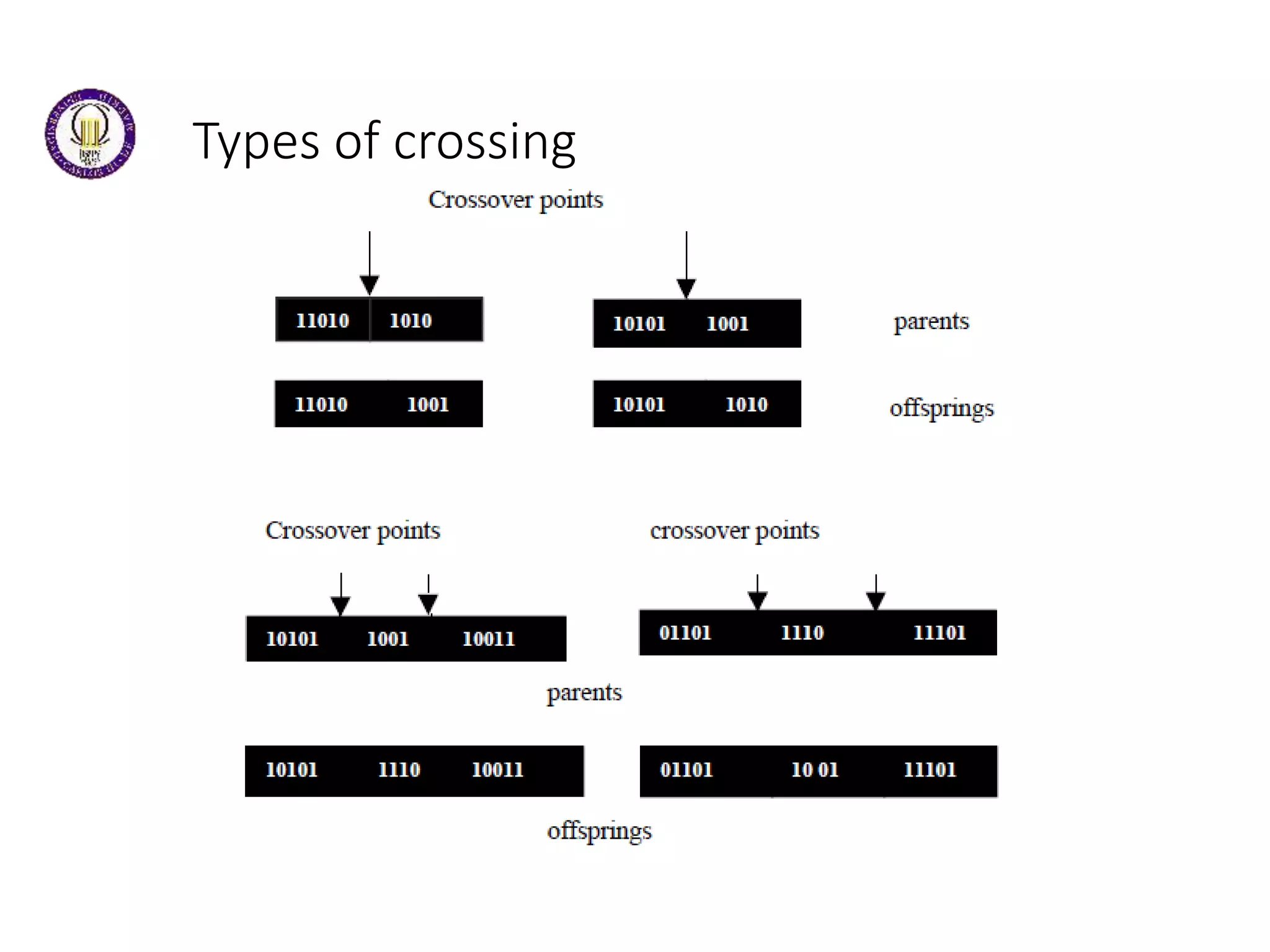
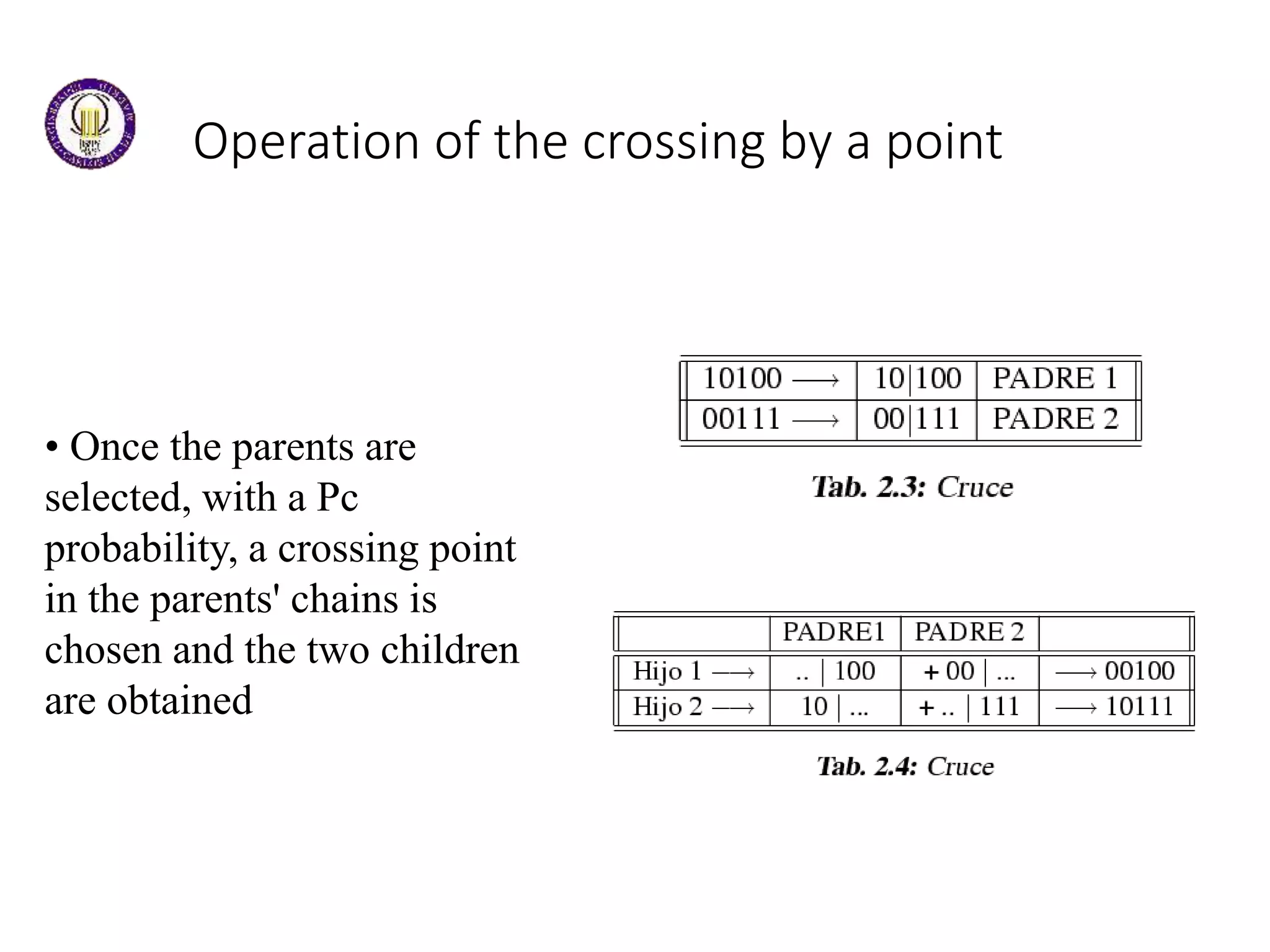
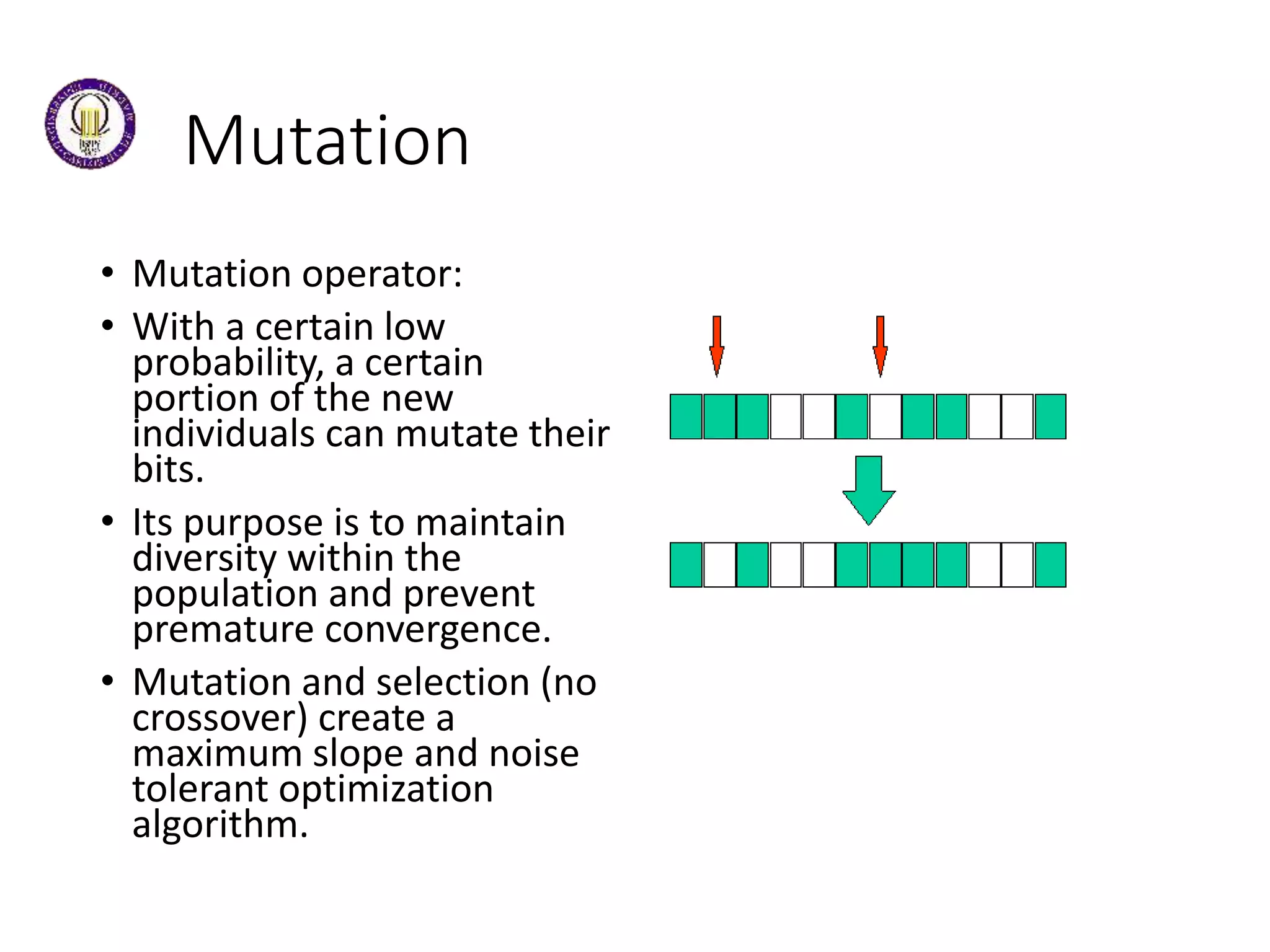
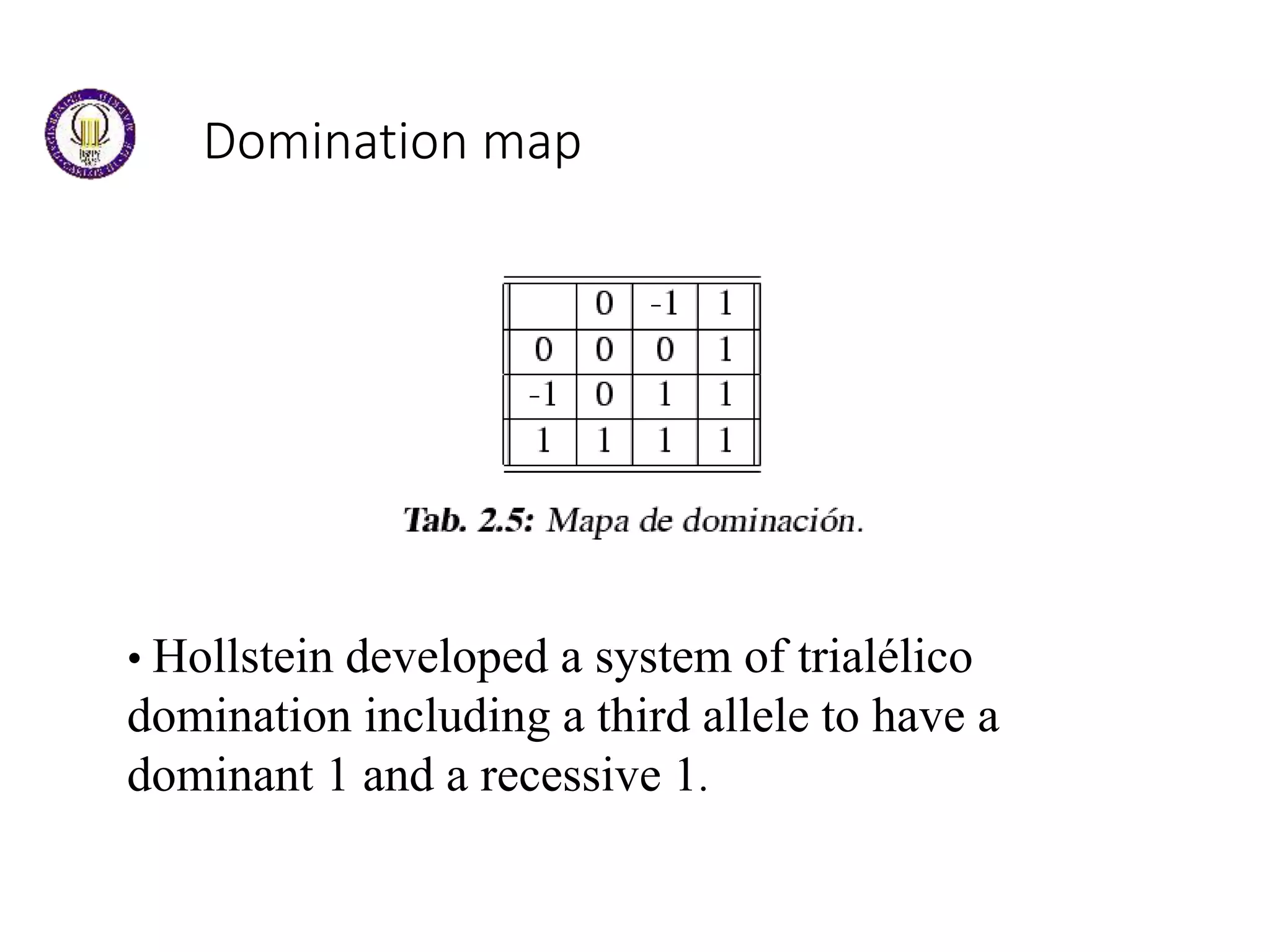
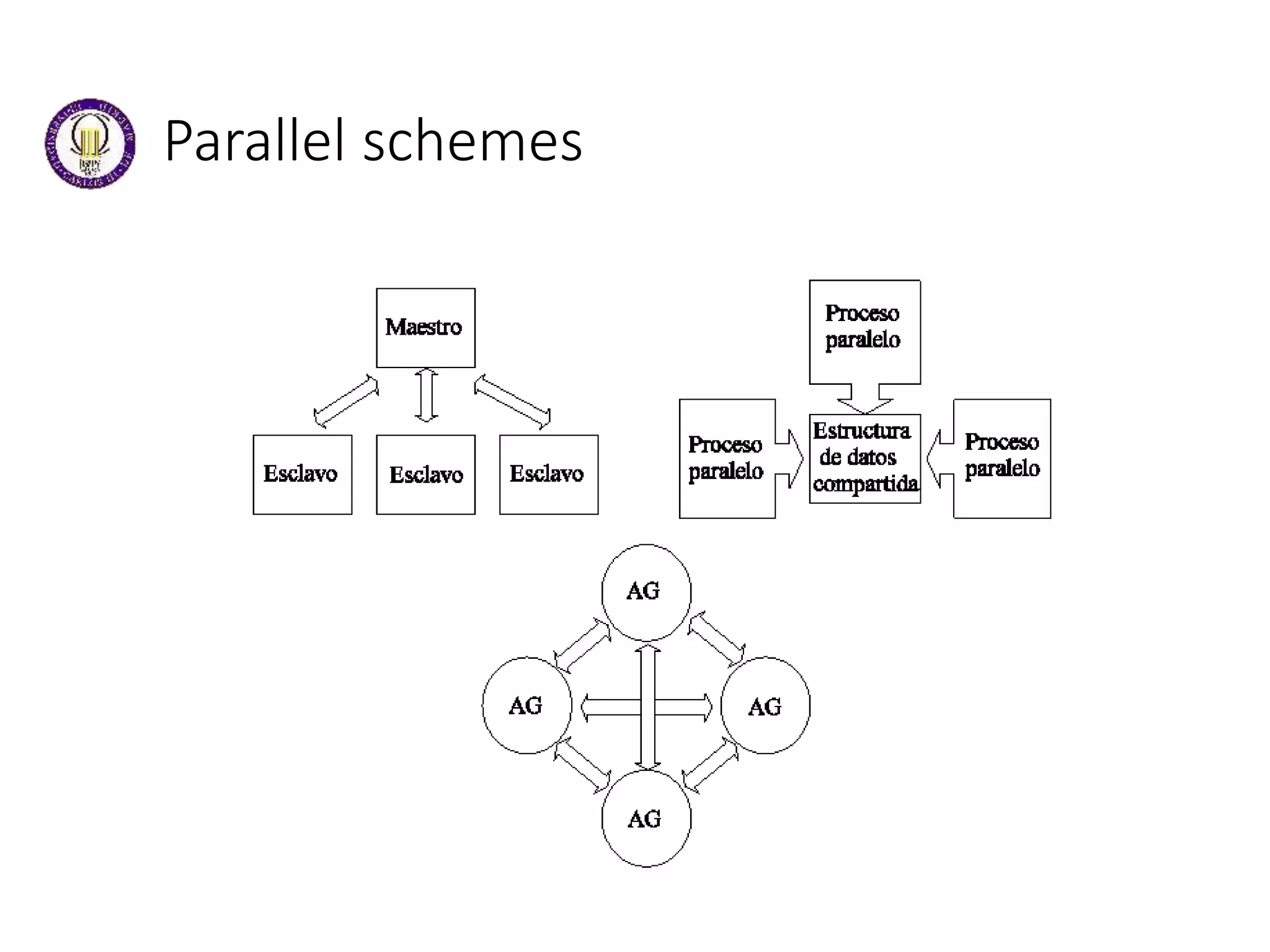
This document discusses genetic algorithms and evolutionary algorithms. It defines genetic algorithms as algorithms that manage populations of coded solutions to search for good solutions. It operates on populations across generations using selection, crossover, and mutation. Key terms discussed include fitness functions, individuals, populations and generations, diversity, and parents and children. The document also introduces differential evolution as a stochastic function optimizer based on populations that uses difference vectors.

1. GENETIC AND
EVOLUTIONARY
ALGORITHMS
DPTO DE INGENIERÍA DE SISTEMAS Y AUTOMÁTICA
UC3M

2. Genetic algorithms
• John Holland, (1975). "Adaptation in natural and
artificial systems.”
• Algorithms that manage populations consisting of
coded solutions of problems.
• The search for good solutions is made in the space of
codified solutions.
• Manipulation of populations: selection, crossing and
mutation.

3. Features
• They do not work with the objects, but with a coding of
them.
• The AG carry out a search through a whole generation of
objects, they do not look for a single element.
• They use a health function that gives us information on
how adapted they are.
• The transition rules are non-deterministic probabilistic.

4. Genetic search

5. Terminology of Genetic Algorithms

6. Cycle of Genetic Algorithms

7. • Key idea: Give
preference to the
best individuals,
allowing them to
pass their genes to
the next generation.
Selection operator
The goodness of an individual is calculated with the
fitness function.

8. Selection methods

9. Selection example for f(x)=x2

10. Crossover operator
• Two individuals of the population
are chosen through the selection
operator.
• A crossing place is randomly chosen.
• The values of the two chains are
exchanged at this point.
• By recombining portions of good
individuals, even better individuals
are created.

11. Types of crossing

12. Operation of the crossing by a point
• Once the parents are
selected, with a Pc
probability, a crossing point
in the parents' chains is
chosen and the two children
are obtained

13. Mutation
• Mutation operator:
• With a certain low
probability, a certain
portion of the new
individuals can mutate their
bits.
• Its purpose is to maintain
diversity within the
population and prevent
premature convergence.
• Mutation and selection (no
crossover) create a
maximum slope and noise
tolerant optimization
algorithm.

14. Dominance
•In nature, most of the species associate a genotype with
a pair of chromosomes, where certain alleles dominate
over others (recessive), so that the phenotype is
determined by the combination of these two
chromosomes and by predominance of alleles .

15. Domination map
• Hollstein developed a system of trialélico
domination including a third allele to have a
dominant 1 and a recessive 1.

16. Classical Algorithms Genetic algorithms
They generate a single
point in each iteration.
The sequence of points
approximates the optimal
solution.
GThere will be a
population of points in
each iteration. The best
point of the population
approximates the optimal
solution.
Select the next point in
the sequence for a
deterministic computation.
Select the next population
by means of a computer
that uses a random
number generator.

17. ¿Por qué funcionan los Algoritmos Genéticos?
• Are the AG bits exchanged only?
• What is behind them?
• Holland created a theorem, called
• "Holland's schemes theorem".
• There are some other theorems, some based
in the analysis of Markov chains:
• Is there a chain of different solutions that allows
reaching the optimal solution?

18. Holland’s Theorem
•Basic principle:
• A scheme represents
several points in space.
• A point is represented by
several schemes.

19. Operations of the GA and Schemes
• Two definitions:
• Schema order: (1,1,0, *, *, *, 1, *, *) => order 4
• Length of the scheme: (1,1,0, *, *, *, 1, *, *) => length 6
• The order of a scheme is the number of fixed positions
• (the number of zeros and ones).
• The length of the scheme is the distance between the first and
the last specific position of the chain.

20. Operations of the GA and Schemes
• Selection: good survival for schemes that represent
good individuals.
• Crossing: good survival for short length schemes.
• Mutation: good survival for low order schemes.

21. Conclusion of the scheme theorem
•Short schemes, low order get
better average.
• The schemes receive an
exponentially increasing number
of individuals

22. Computational aspects
• A large number of health assessments can be
computationally expensive.
• They are completely parallel by nature.
• There are several good schemes for parallel
computing.

23. Parallel schemes

24. Genetic Algorithms with continuous
parameters
• One of the problems with binary coding in genetic
algorithms is that you do not normally take advantage
of all the precision of the computer.
• What can be done if you want to use all the possible
precision?
• The answer is to represent the parameters in floating
point.
• When the variable is continuous, this is the most
natural way to represent the numbers. It also has the
advantage that a smaller memory size is required than
for binary storage.

25. Genetic Algorithms with continuous
parameters
• Operators do not usually work at the bit level as in the
binary case, but work at the level of the whole floating-
point number:
• Selection: The chromosomes are ordered according to their
health and we are left with the best members of the
population.
• Crossing: In the simplest methods, one or more points are
chosen on the chromosome to mark the crossing points.
Then the parameters between these points are simply
exchanged between the two parents.

26. Genetic Algorithms with continuous
parameters
• Mutation: With a certain probability, which is usually
between 1% and 20%, the chromosomes that are going to
be mutated are selected.
• Next, the parameters of the chromosome that are to be
mutated are randomly selected.
• Finally, each parameter to be mutated is replaced by
another new random parameter or another new random
parameter is added.

27. Some Genetic Algorithm
Terminology
• Fitness Functions
• The fitness function is the function you want to
optimize. For standard optimization algorithms, this is
known as the objective function.
• The toolbox tries to find the minimum of the fitness
function. You can write the fitness function as an M-file
and pass it as a function handle input argument to the
main genetic algorithm function.

28. Some Genetic Algorithm
Terminology
• Individuals
• An individual is any point to which you can apply the
fitness function. The value of the fitness function for an
individual is its score.
• For example, if the fitness function is the vector (2, 3, 1),
whose length is the number of variables in the problem,
is an individual. The score of the individual (2, 3, 1) is f(2,
-3, 1) = 51. An individual is sometimes referred to as a
genome and the vector entries of an individual as genes.

29. Some Genetic Algorithm
Terminology
• Populations and Generations
• A population is an array of individuals. For example, if the size of
the population is 100 and the number of variables in the fitness
function is 3, you represent the population by a 100-by-3 matrix.
• The same individual can appear more than once in the
population. For example, the individual (2, 3, 1) can appear in
more than one row of the array.
• At each iteration, the genetic algorithm performs a series of
computations on the current population to produce a new
population. Each successive population is called a new generation.

30. Some Genetic Algorithm
Terminology
• Diversity
• Diversity refers to the average distance between individuals in a
population. A population has high diversity if the average distance
is large; otherwise it has low diversity. In the figure, the population
on the left has high diversity, while the population on the right has
low diversity.
• Diversity is essential to the genetic algorithm because it enables
the algorithm to search a larger region of the space.

31. Some Genetic Algorithm
Terminology
• Fitness Values and Best Fitness Values
• The fitness value of an individual is the value of the
fitness function for that individual.
• Because the toolbox finds the minimum of the
fitness function, the best fitness value for a
population is the smallest fitness value for any
individual in the population.

32. Some Genetic Algorithm
Terminology
• Parents and Children
• To create the next generation, the genetic
algorithm selects certain individuals in the current
population, called parents, and uses them to create
individuals in the next generation, called children.
• Typically, the algorithm is more likely to select
parents that have better fitness values.

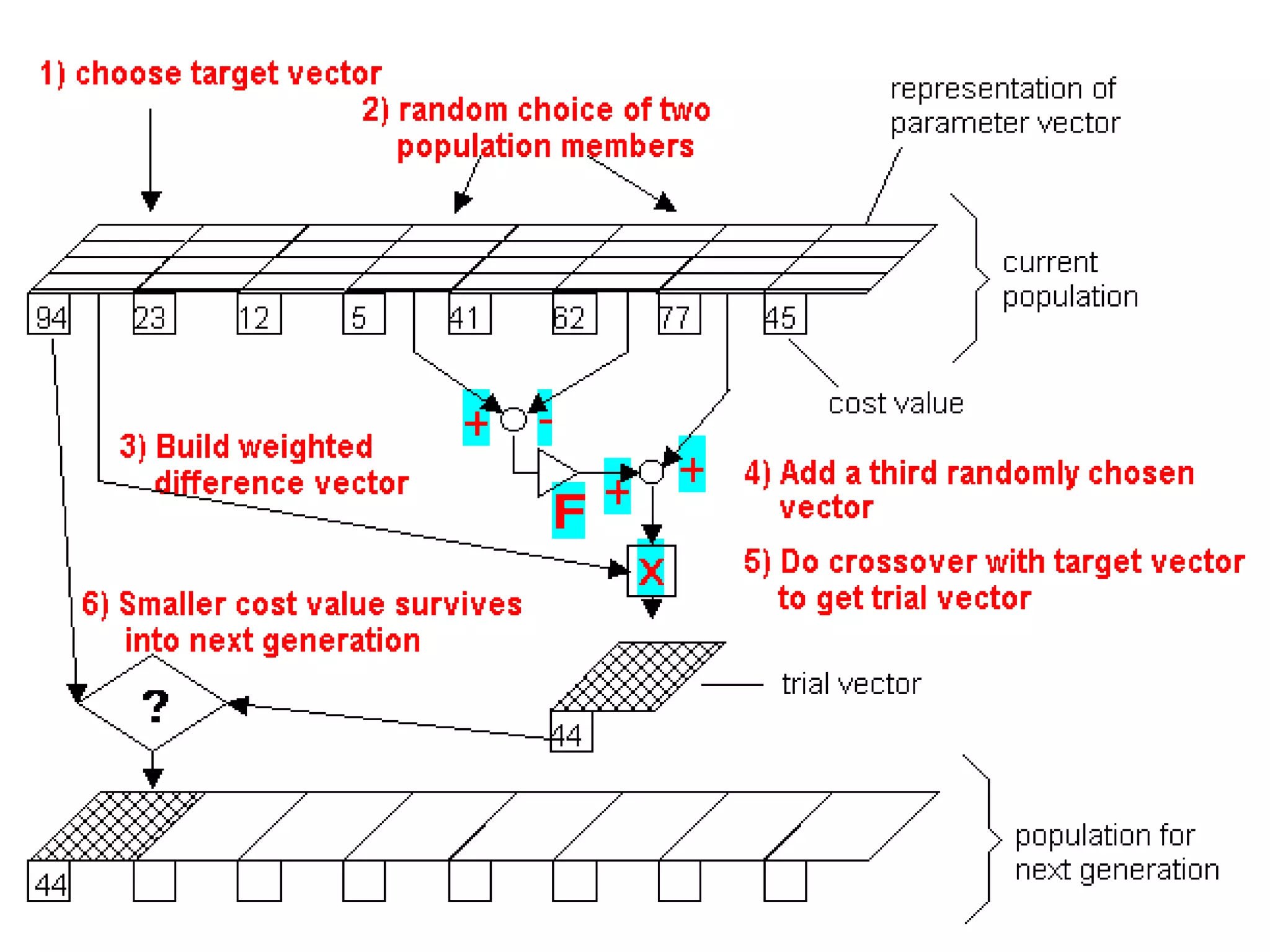
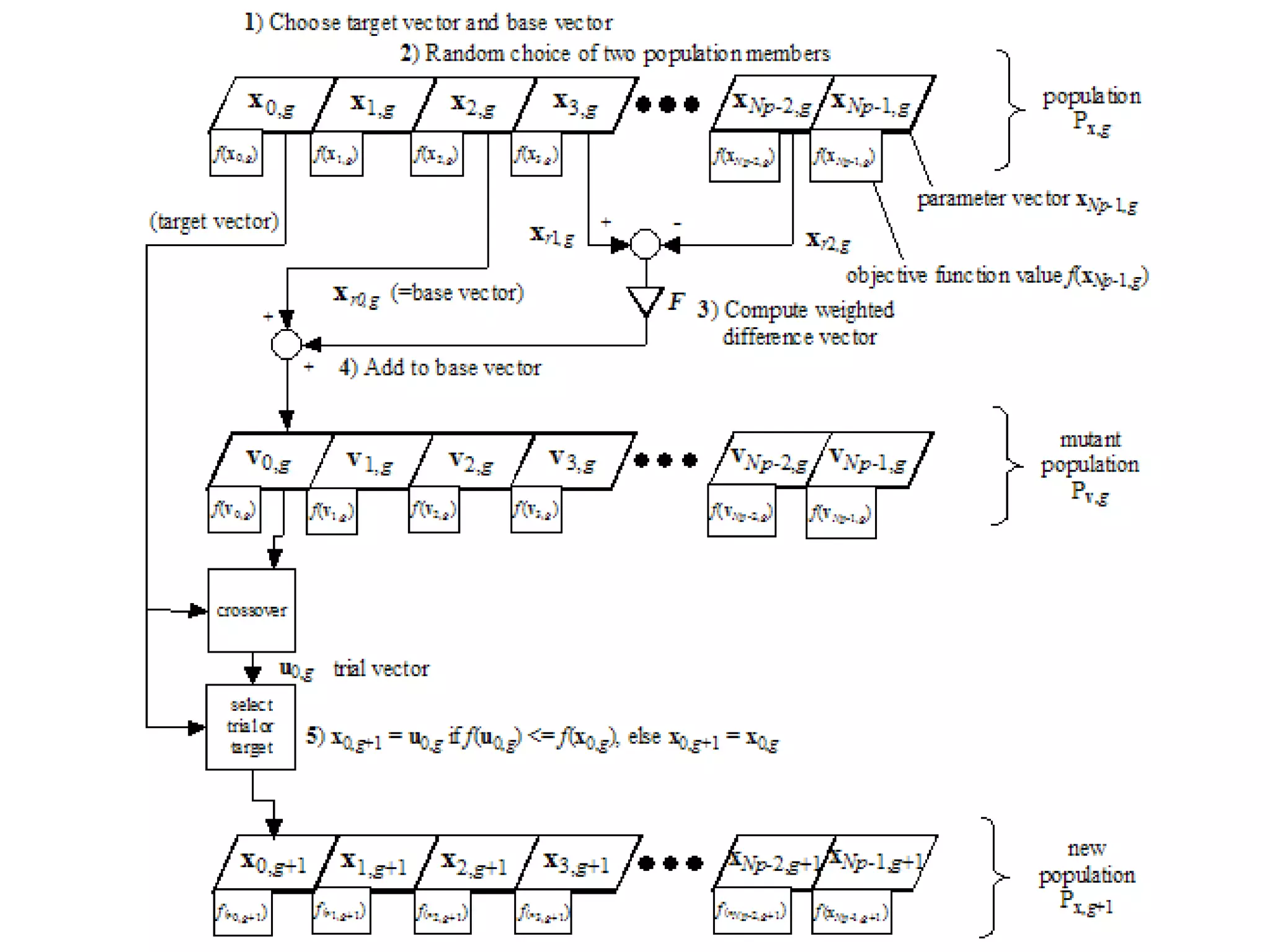
33. Differential Evolution
• Differential Evolution (DE) is a stochastic function optimizer, based on
populations, that uses the difference vector to disturb the population.
• DE shows advantages of speed and performance over conventional
genetic algorithms.
• DE was originally proposed by Kenneth Price and Rainer Storn [1997].
• The crucial idea behind DE is the scheme for generating vectors of test
parameters in which the difference (with weight) between vectors is
added to a selected vector.

34. Differential Evolution