Download as PDF, PPTX
Uploaded byJay Wacker
Composite Inelastic Dark Matter
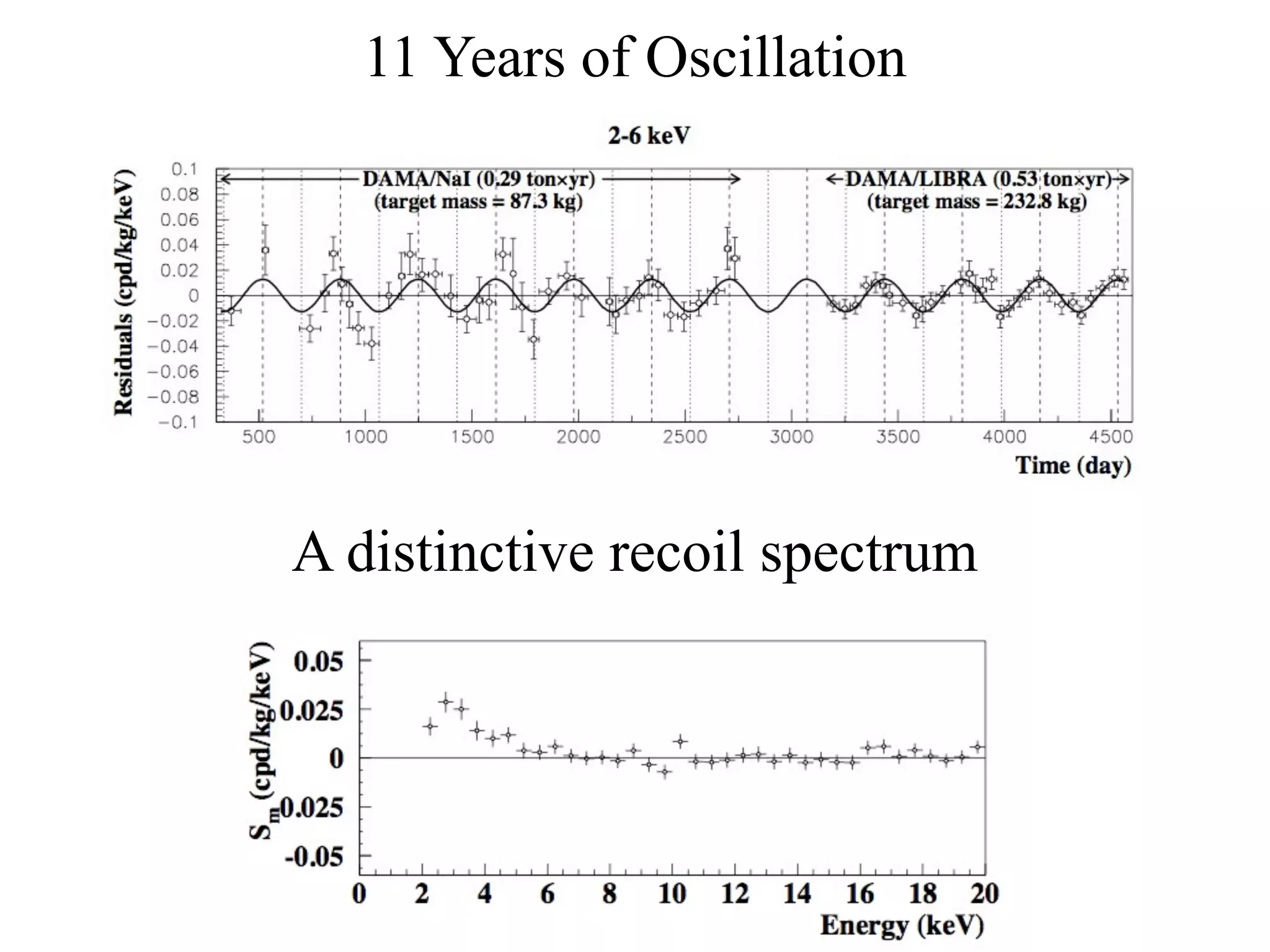
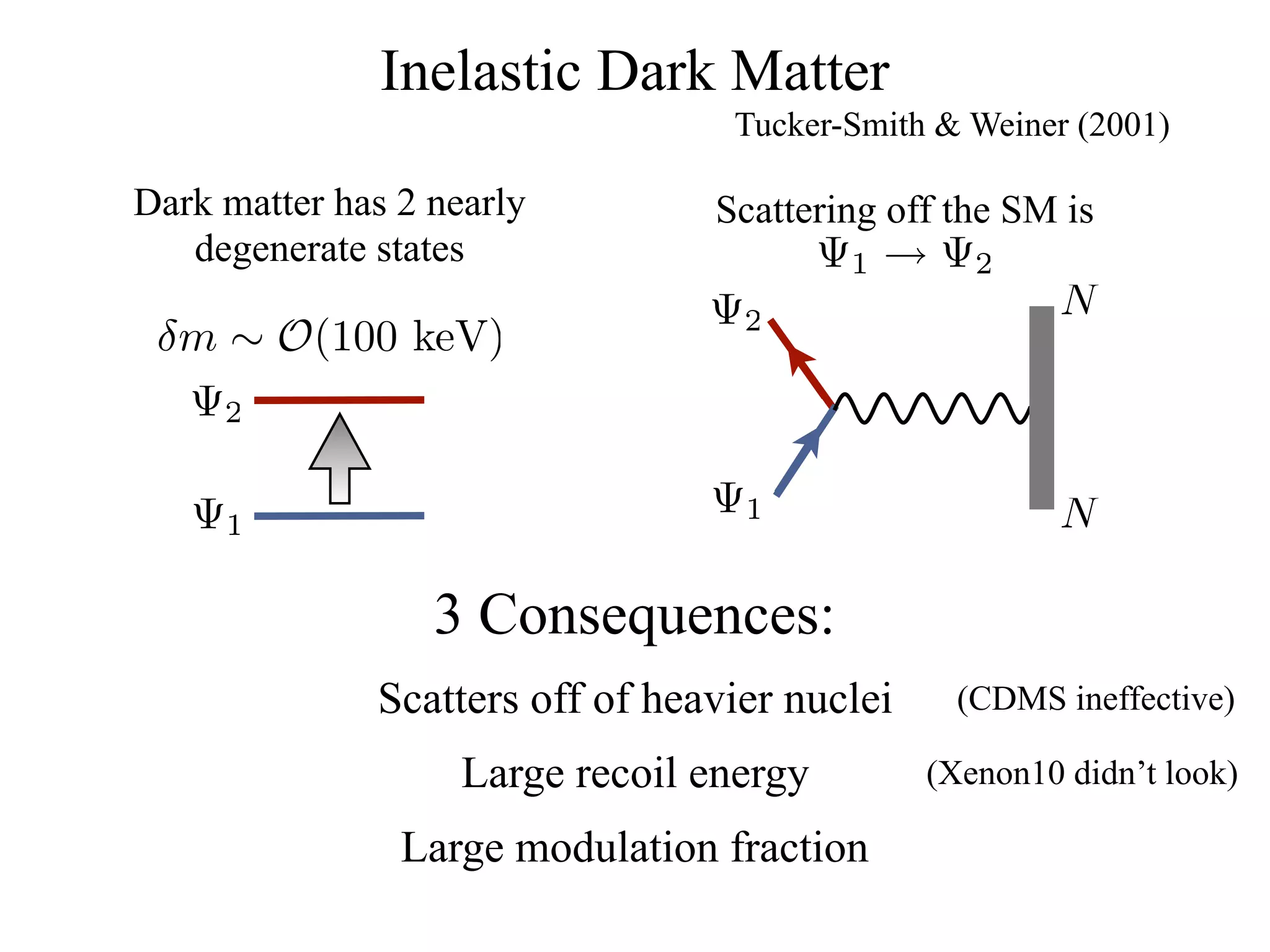
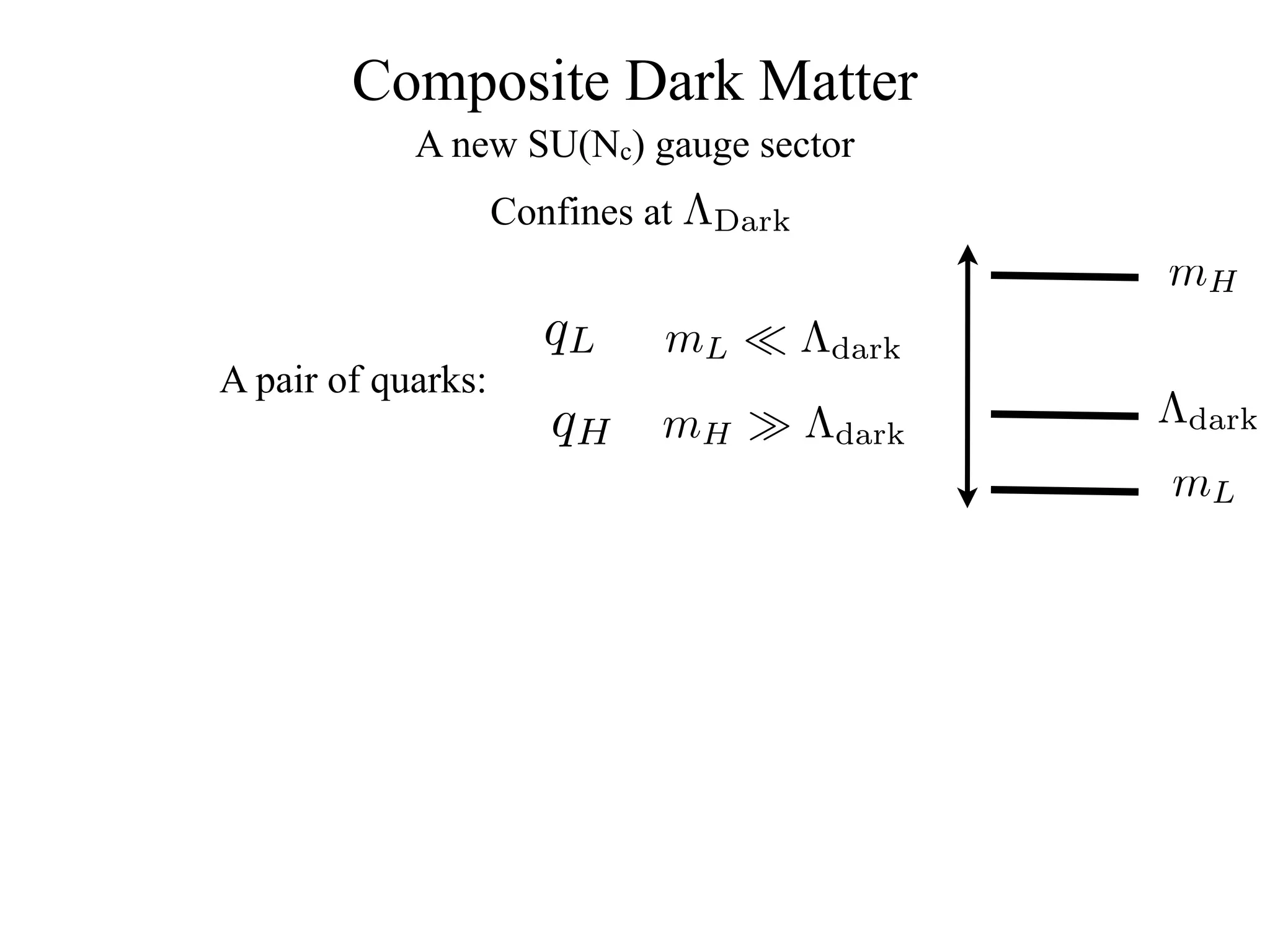
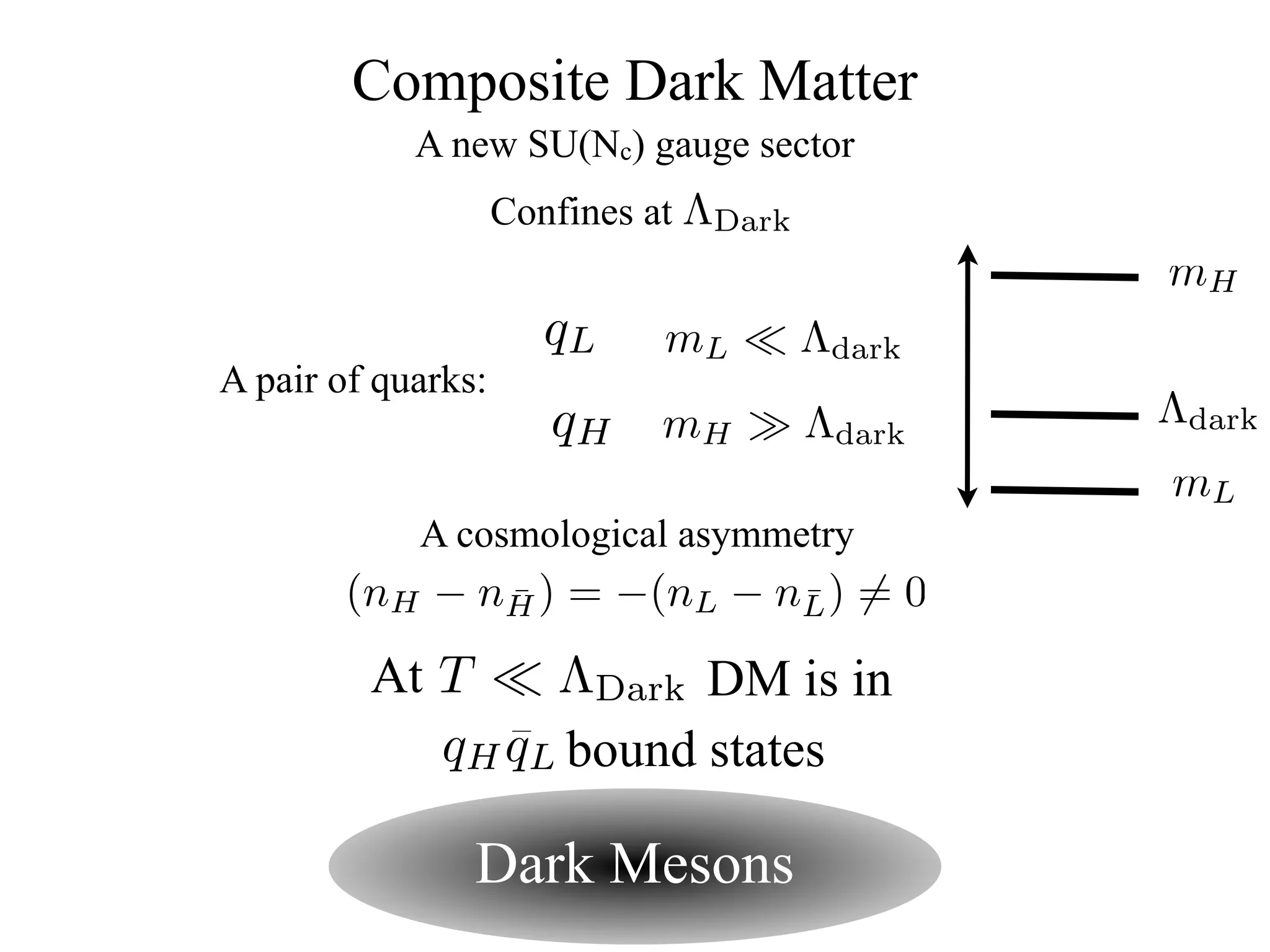
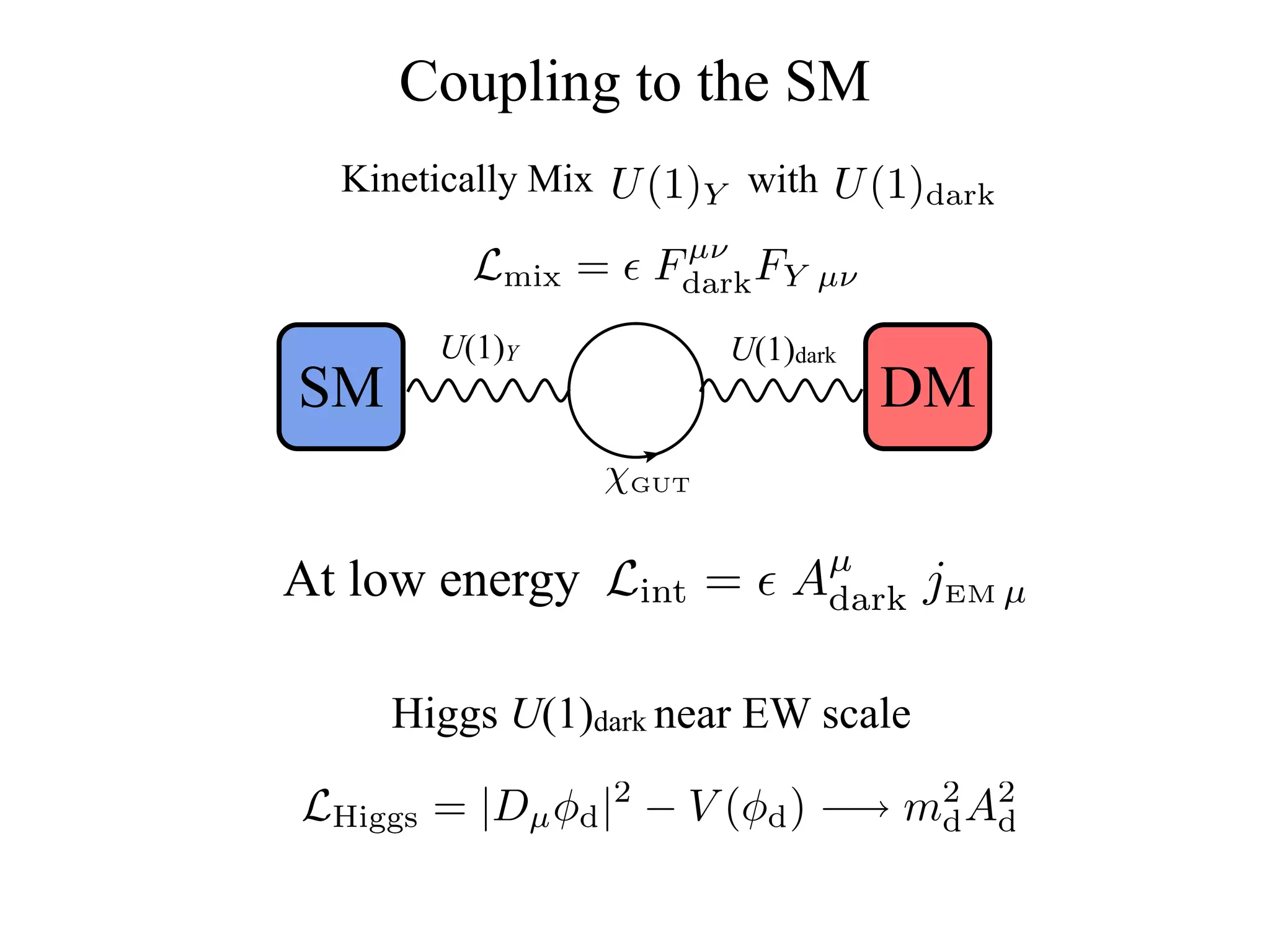
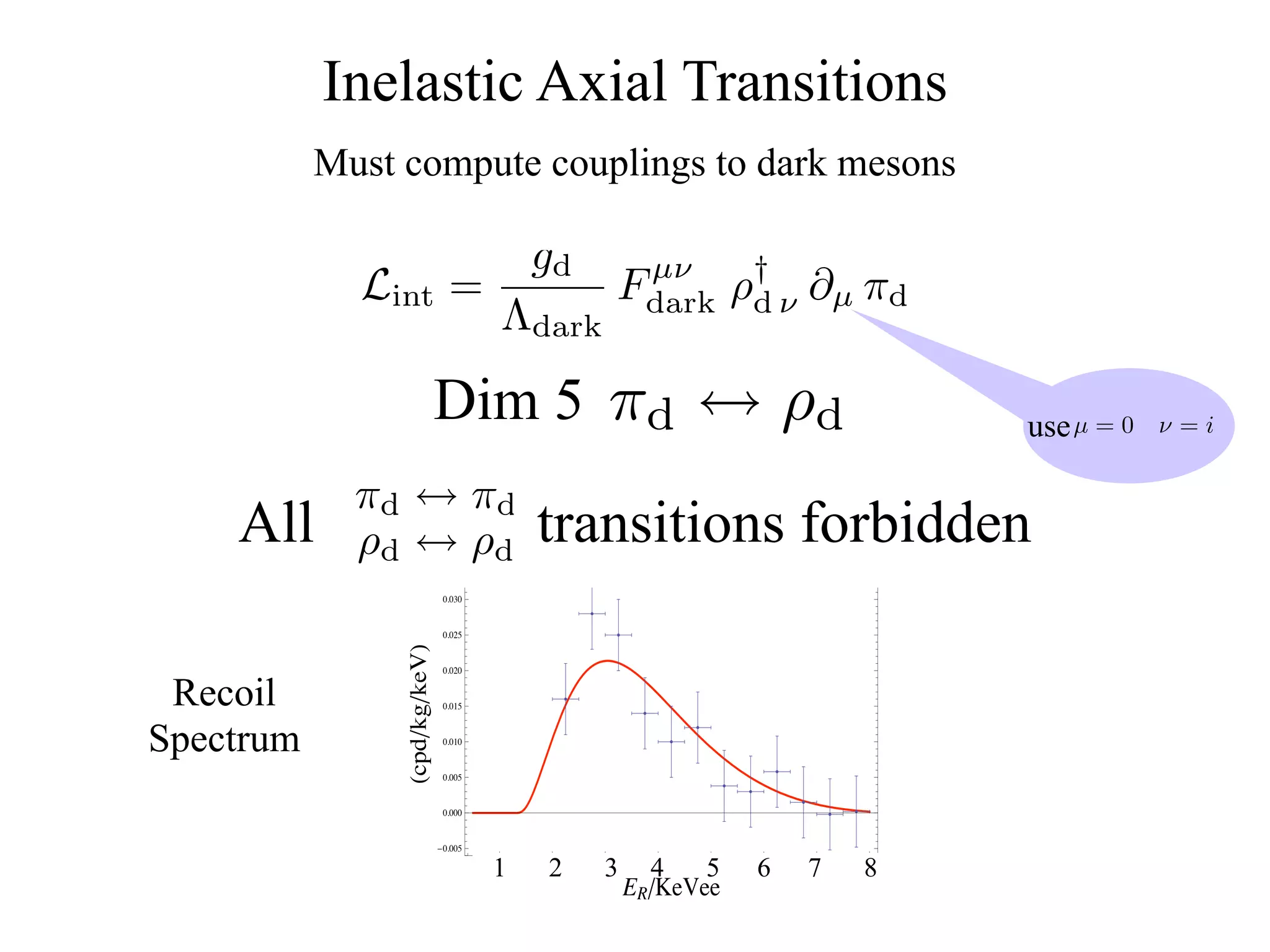
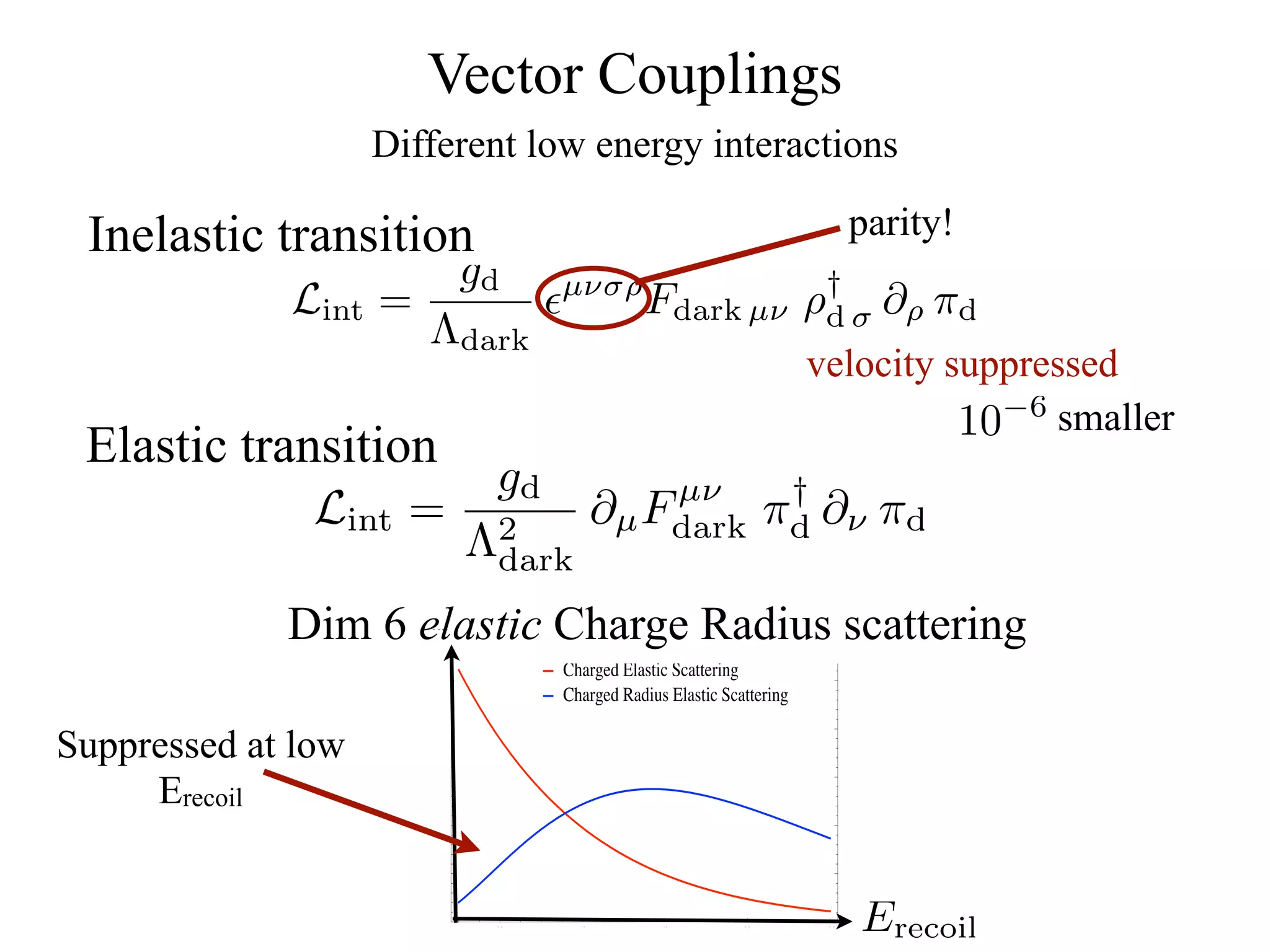
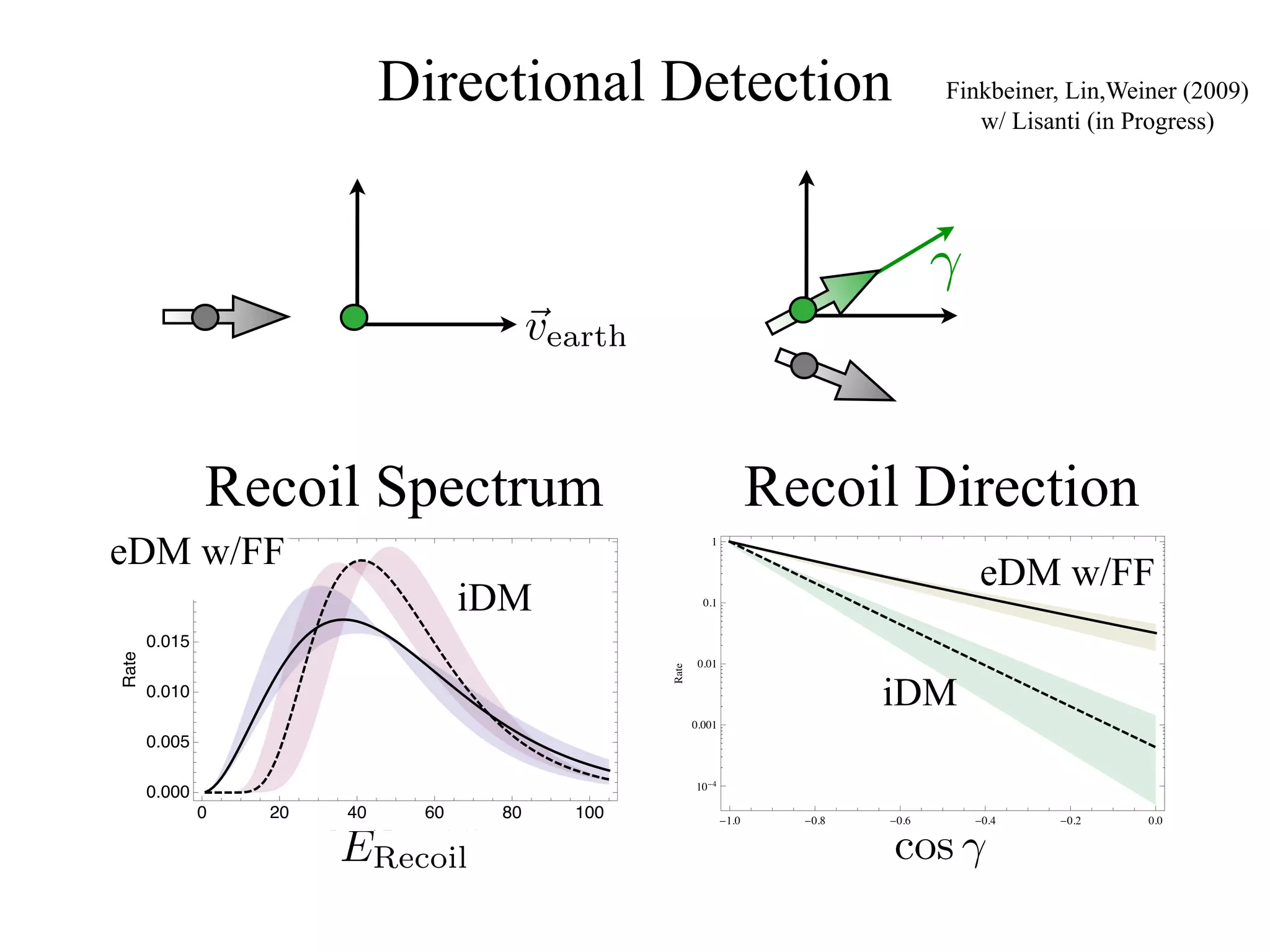
The document discusses composite inelastic dark matter and its implications for particle physics, focusing on distinctive recoil spectra and the dynamics within a new SU(Nc) gauge sector. It explores concepts such as degenerate states, scattering off heavier nuclei, and the potential for new experimental observations to better understand dark matter interactions. The outlook suggests that further studies and experiments are necessary to uncover the complexities and dynamics of dark matter, with various models and collider signatures to be investigated.
Composite Inelastic Dark Matter
- 1. Composite Inelastic DarkMatter Jay Wacker SLAC June 6, 2009 arXiv:0903.3945 With Philip Schuster Siavosh Behabani Daniele Alves
- 2. 11 Years ofOscillation A distinctive recoil spectrum
- 3. Inelastic Dark Matter Tucker-Smith & Weiner (2001) Dark matter has 2 nearly Scattering off the SM is degenerate states Ψ1 → Ψ2 Ψ2 N δm ∼ O(100 keV) Ψ2 Ψ1 Ψ1 N 3 Consequences: Scatters off of heavier nuclei (CDMS ineffective) Large recoil energy (Xenon10 didn’t look) Large modulation fraction
- 4. Inelastic Dark Matter A new number to explain: δm m ∼ 10 −6 Breaking of an approximate global symmetry Like Yukawas Radiatively stable Hard to discover origin Sign of dark sector dynamics First of many splittings New interactions to discover Changes what questions are interesting
- 5. Composite Dark Matter A new SU(Nc) gauge sector Confines at ΛDark mH qL mL Λdark A pair of quarks: qH mH Λdark Λdark mL
- 6. Composite Dark Matter A new SU(Nc) gauge sector Confines at ΛDark mH qL mL Λdark A pair of quarks: qH mH Λdark Λdark mL A cosmological asymmetry (nH − nH ) = −(nL − nL ) = 0 ¯ ¯ At T ΛDark DM is in ¯ qH qL bound states Dark Mesons
- 7. Degeneracy of theGround State Heavy quark spin preserved in electric interactions Dark Chromomagnetic interaction breaks spin symmetry ¯ qH qL ρd m σ·B πd δH ∼ mH Spin 0 Spin 1 Dark Pion Dark Rho πd ρd mρd − mπd Λ2 ∼ Dark mH Doesn’t require adding new symmetry and breaking it Accidental global symmetry from Lorentz Invariance
- 8. Coupling to theSM Kinetically Mix U (1)Y with U (1)dark µν Lmix = Fdark FY µν U(1)Y U(1)dark SM DM χGUT µ At low energy Lint = Adark jEM µ Higgs U(1)dark near EW scale LHiggs = |Dµ φd | − V (φd ) −→ 2 2 2 md Ad
- 9. Charging the DarkQuarks Two Choices Anomaly-Free Charges Vector coupling µ jdark = gd (¯H γ qH − qL γ qL ) q µ ¯ µ Doesn’t forbid dark quark masses Has both elastic and inelastic scattering channels
- 10. Charging the DarkQuarks Two Choices Anomaly-Free Charges Vector coupling µ jdark = gd (¯H γ qH − qL γ qL ) q µ ¯ µ Doesn’t forbid dark quark masses Has both elastic and inelastic scattering channels Axial Vector coupling µ jdark = gd (¯H γ γ qH − qL γ γ qL ) q µ 5 ¯ µ 5 Forbids dark quark masses until U(1)dark Higgsing Only inelastic scattering channels
- 11. Inelastic Axial Transitions Must compute couplings to dark mesons gd µν † Lint = Fdark ρd ν ∂µ πd Λdark Dim 5 πd ↔ ρd use µ = 0 ν=i πd ↔ πd All ρd ↔ ρd transitionsA forbidden MDM 200 GeV, 125 keV, M 1 GeV 0.030 0.025 cpd kg keV 0.020 Recoil 0.015 Spectrum 0.010 0.005 0.000 0.005 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 ER KeVee
- 12. Vector Couplings Different low energy interactions Inelastic transition parity! gd † Lint = µνσρ Fdark µν ρd σ ∂ρ πd Λdark velocity suppressed 10 −6 smaller Elastic transition gd µν † Lint = 2 ∂µ Fdark πd ∂ν πd Λdark Dim 6 elastic Charge Radius scattering
- 13. Vector Couplings Different low energy interactions Inelastic transition parity! gd † Lint = µνσρ Fdark µν ρd σ ∂ρ πd Λdark velocity suppressed 10 −6 smaller Elastic transition gd µν † Lint = 2 ∂µ Fdark πd ∂ν πd Λdark Dim 6 elastic Charge Radius scattering 200 GeV, M 200 GeV, M 1 GeV MDM0.030 DM A 125 keV, M Count Rate arbitraty units 0.030 0.025 Charged Elastic Scattering Charged Radius Elastic Scattering 0.025 cpd kg keV Suppressed at low 0.020 0.020 0.015 Erecoil 0.015 0.010 0.010 0.005 0.005 0.000 0.000 20 40 60 80 100 Erecoil 0.005 1 2 3 4 5 6
- 14. CP-Violation Add θ term to dark QCD sector Spin 1 sector ˜ LCPV = θGµν Gµν Mixes states of opposite CP Λdark l = 1, s = 0 i.e. ρd & a1 d mix l = 0, s = 1 gd Allows Lint = µν † Fdark ρd ν ∂µ πd Λdark Both inelastic & form-factor suppressed elastic interactions Nearly the same Recoil Spectra How to measure?
- 15. Directional Detection Finkbeiner, Lin,Weiner (2009) w/ Lisanti (in Progress) γ vearth Recoil Spectrum Recoil Direction eDM w/FF 0.025 1 eDM w/FF 0.020 iDM 0.1 0.015 Rate 0.01 Rate 0.010 iDM 0.001 0.005 4 10 0.000 0 20 40 60 80 100 1.0 0.8 0.6 0.4 0.2 0.0 ERecoil Recoil Energy keV cos γ Cos Γ
- 16. Outlook Composite inelastic DM gives explanation to 100 keV scale Lots of variants with different scattering New experiments needed to understand DM dynamics Collider signatures of DM could have showering Lots of models to explore Susy & Dark Flavor