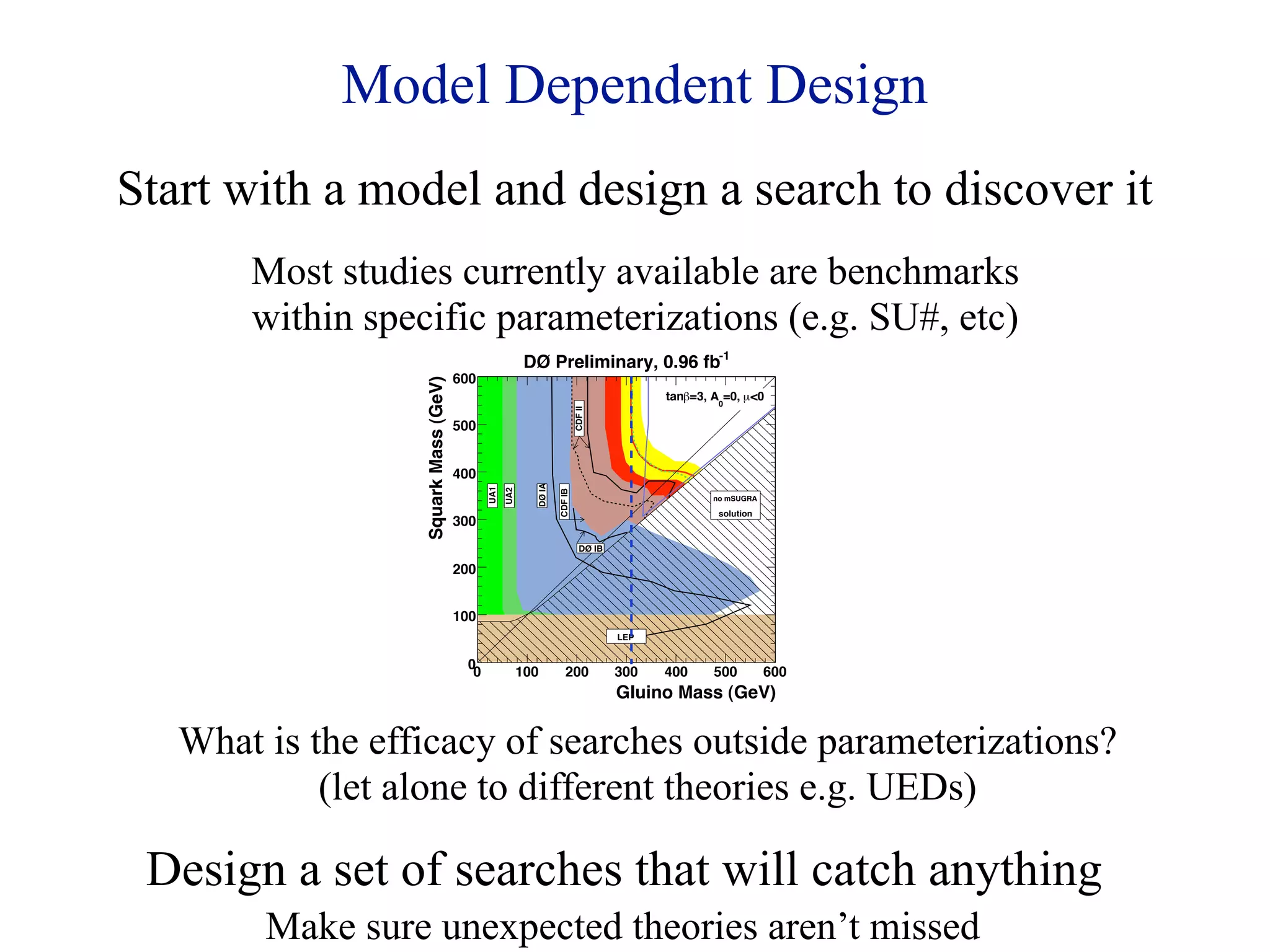
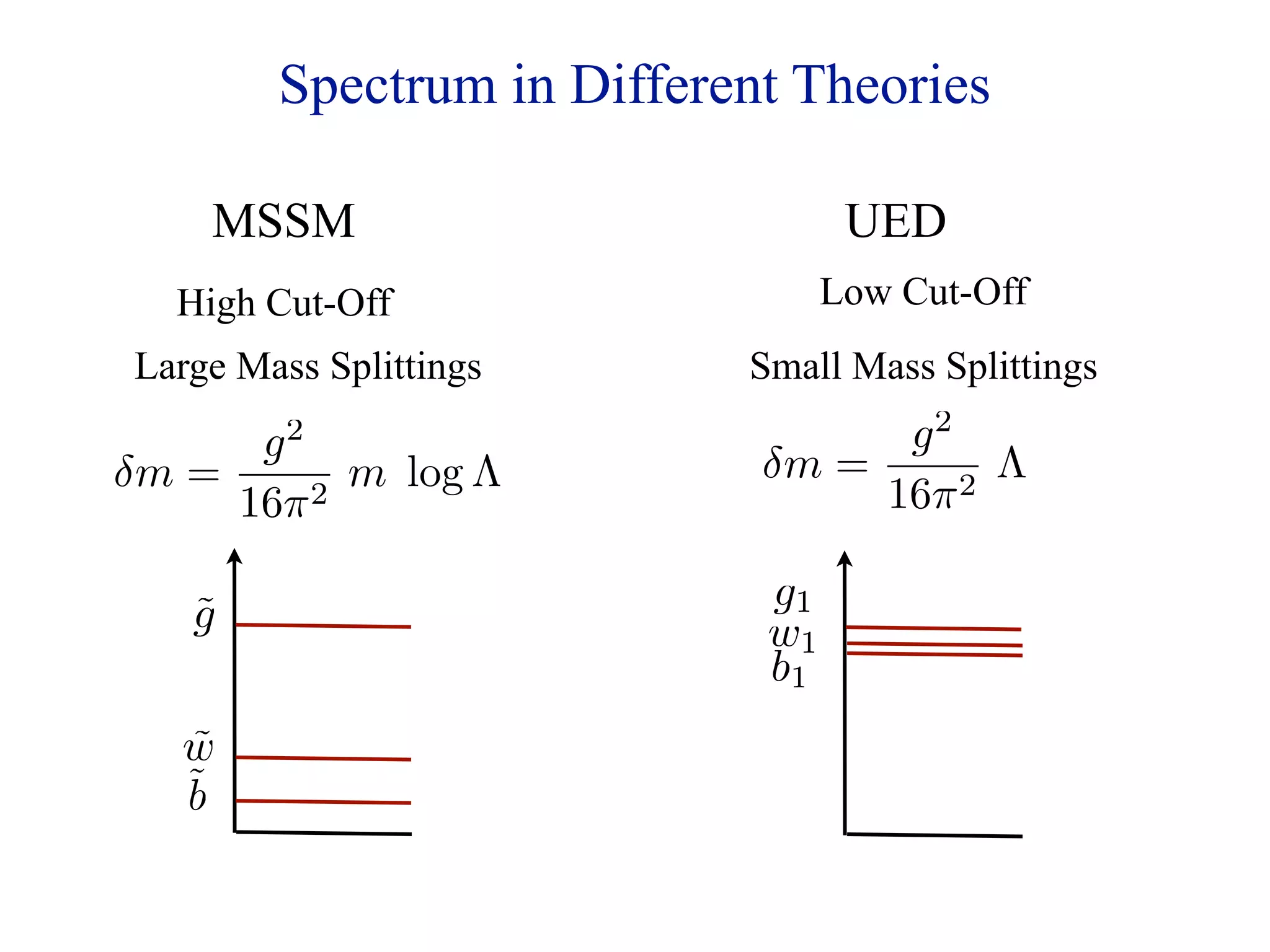
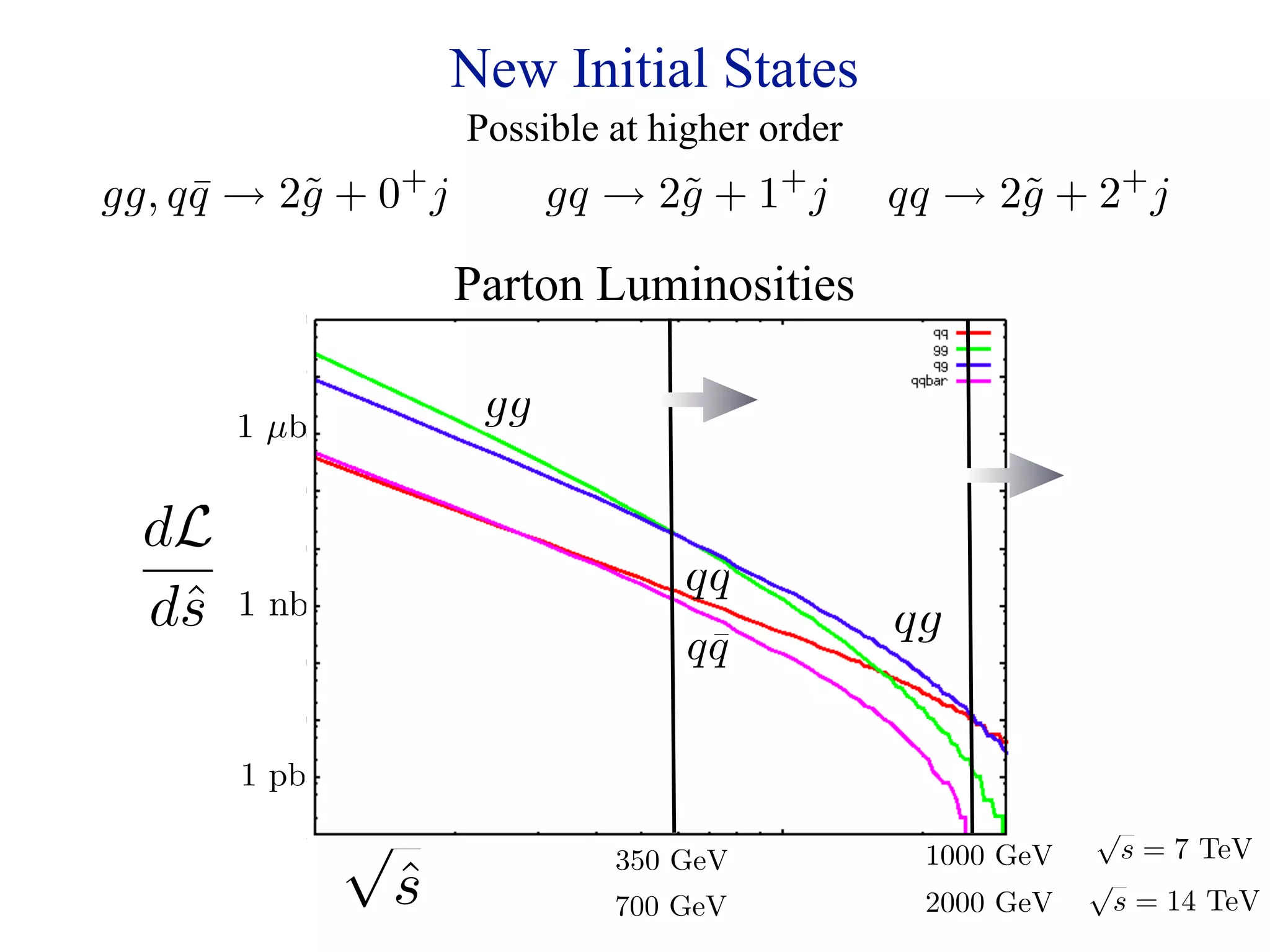
This document discusses the challenges in particle phenomenology related to jets and missing transverse energy (met) searches in the context of the hierarchy problem and dark matter models. It presents model-independent search strategies for identifying new physics, particularly focusing on pairs of gluinos decaying to binos, and highlights the importance of differential mass relations on search efficacy. Various searches are proposed to optimize detection and exclusion limits for different mass configurations while addressing background noise from Standard Model processes.

1. Jets Plus MET:
Now versus Then
Jay Wacker
SLAC
Emerging problems in particle phenomenology
April 11, 2010
with Eder Izaguirre, Ning Bao and Michael Manhart
arXiv: 1003.3886, 1004.XXXX
“I swear it’s right around the corner”

2. Jets + MET
Solution to Hierarchy Problem
If the symmetry commutes with SU(3)C,
new colored top partners
(note twin Higgs exception)
Dark Matter
Wimp Miracle: DM a thermal relic if
mass is 100 GeV to 1 TeV
Usually requires a dark sector,
frequently contains new colored particles
Fewest requirements on spectroscopy
Doesn’t require squeezing in additional states to decay chains

3. Model Dependent Design
Start with a model and design a search to discover it
Most studies currently available are benchmarks
within specific parameterizations (e.g. SU#, etc)
DØ Preliminary, 0.96 fb-1
600
Squark Mass (GeV)
tan!=3, A =0, µ <0
0
CDF II
500
400
DØ IA
UA1
UA2
CDF IB
no mSUGRA
solution
300
DØ IB
200
100
LEP
0
0 100 200 300 400 500 600
Gluino Mass (GeV)
What is the efficacy of searches outside parameterizations?
(let alone to different theories e.g. UEDs)
Design a set of searches that will catch anything
Make sure unexpected theories aren’t missed

4. Spectrum in Different Theories
MSSM UED
High Cut-Off Low Cut-Off
Large Mass Splittings Small Mass Splittings
2
g 2 g
δm = m log Λ δm = Λ
16π 2 16π 2
˜
g g1
w1
b1
˜
w
˜
b

5. Tevatron Review
Searches are challenging
Difficult to pull signal from background
Necessary to consider multiple searches
1j + E T 2j + E T 3j + E T 4+ j + E T
Multiple cuts for E T HT
Frequently low values of E T HT are necessary

6. Casting a Wide Net
Kinematics matters more than spin or A-terms
Alwall, Le Lisanti, JW (0803.0019)
Q = mX − mχ ˜
X = g , q , ...
˜ ˜
Q=0
V. GLUINO EXCLUSION LIMITS
A. No Cascade Decays
˜
χ
m
For the remainder of the paper, we will discuss how model-independent jets + ET searches
can be used to set limits on the parameters in a particular theory. We will focus specifically
=
on the case of pair-produced gluinos at the Tevatron and begin by considering the simplified
scenario of a direct decay to the bino. The expected number of jets depends on the relative
mχ
mass difference between the gluino and bino. When the mass difference is small, the decay
jets are very soft and initial-state radiation is important; in this limit, the monojet search
˜ is best. When the mass difference is large, the decay jets are hard and well-defined, so
the multijet search is most effective. The dijet and threejet searches are important in the
transition between these two limits.
X
m
As an example, let us consider the model spectrum with a 340 GeV gluino decaying
directly into a 100 GeV bino. In this case, the gluino is heavy and its mass difference with
the bino is relatively large, so we expect the multijet search to be most effective. Table III
shows the differential cross section grids for the 1-4+ jet searches for this simulated signal
point. The colors indicate the significance of the signal over the limits presented in Table II;
the multijet search has the strongest excesses.
Tevatron Gluino
Previously [28], we obtained exclusion limits by optimizing the ET and HT cuts, which
involves simulating each mass point beforehand to determine which cuts are most appropri-
ate. This is effectively like dealing with a 1 × 1 grid, for which a 95% exclusion corresponds
250 GeV Sensitivity
150
mSugra
Bino Mass GeV
100
Out[27]=
50 X
0
100 200
Gluino Mass GeV
300 400 500
FIG. 4: The 95% exclusion region for DO at 4 fb−1 assuming 50% systematic error on background.
mX
250 GeV
The exclusion region for a directly decaying gluino is shown in light blue; the worst case scenario
500 GeV
for the cascade decay is shown in dark blue. The dashed line represents the CMSSM points and
the “X” is the current DO exclusion limit at 2 fb−1 .
15

7. Plan of Talk
Distinguishing Signal from Background
*
Where the LHC can get to (soon)

8. 542 than 20 GeV. We demand at least 4 jets with |η |
pT 100 GeV. The transverse sphericity ST should
Backgrounds
543
544 ETmiss should be larger than 100 GeV and larger th
545 add one more cut against the QCD background: the
Madgraph+Pythia 546
547
between the ET PGS
miss vector and the three highest-p
discussed in a dedicated note on QCD background e
(up to 2 → 4 )
548 3.2 Backgrounds in Monte Carlo
4+jetsFigure 16 shows the distributions of E
549
miss
T and Meff
SM 104
¯
Events / 1fb−1/ 50GeV
1000 SU3
tt± SM BG
tt
W 103 W
(fb/25 GeV)
100 Z0 Z
QCD
QCD 102
single top
ATLAS
10
10
dET
dσ
1
1
0 100 200 300 400 500 600 700 800 900 1000
Missing ET [GeV]
0.1
200 400 600 800
√1000
ET (GeV)
s = 14 TeV
Figure 16: The ET miss and effective mass distribut
for the no-lepton mode with an integrated luminosit
(SU3 point). The shaded histogram shows the sum o
Matching crucial to getting MET tail vaguely right
show the various components.

9. Signals
Should use same methods for signals as backgrounds
Signal may be in a different place than expected
Parton Shower - Matrix Element Matching
pp → XX + 0j pp → XX + 1j pp → XX + 2 j
+
Extra jets aren’t a nuisance,
they can qualitatively alter signal

10. New Initial States
Possible at higher order
gg, q q → 2˜ + 0+ j
¯ g gq → 2˜ + 1+ j
g qq → 2˜ + 2+ j
g
Parton Luminosities
1 µb
gg
dL
qq
dˆ
s 1 nb qg
¯
qq
1 pb
√ 350 GeV 1000 GeV
√
s = 7 TeV
ˆ
s 700 GeV 2000 GeV
√
s = 14 TeV

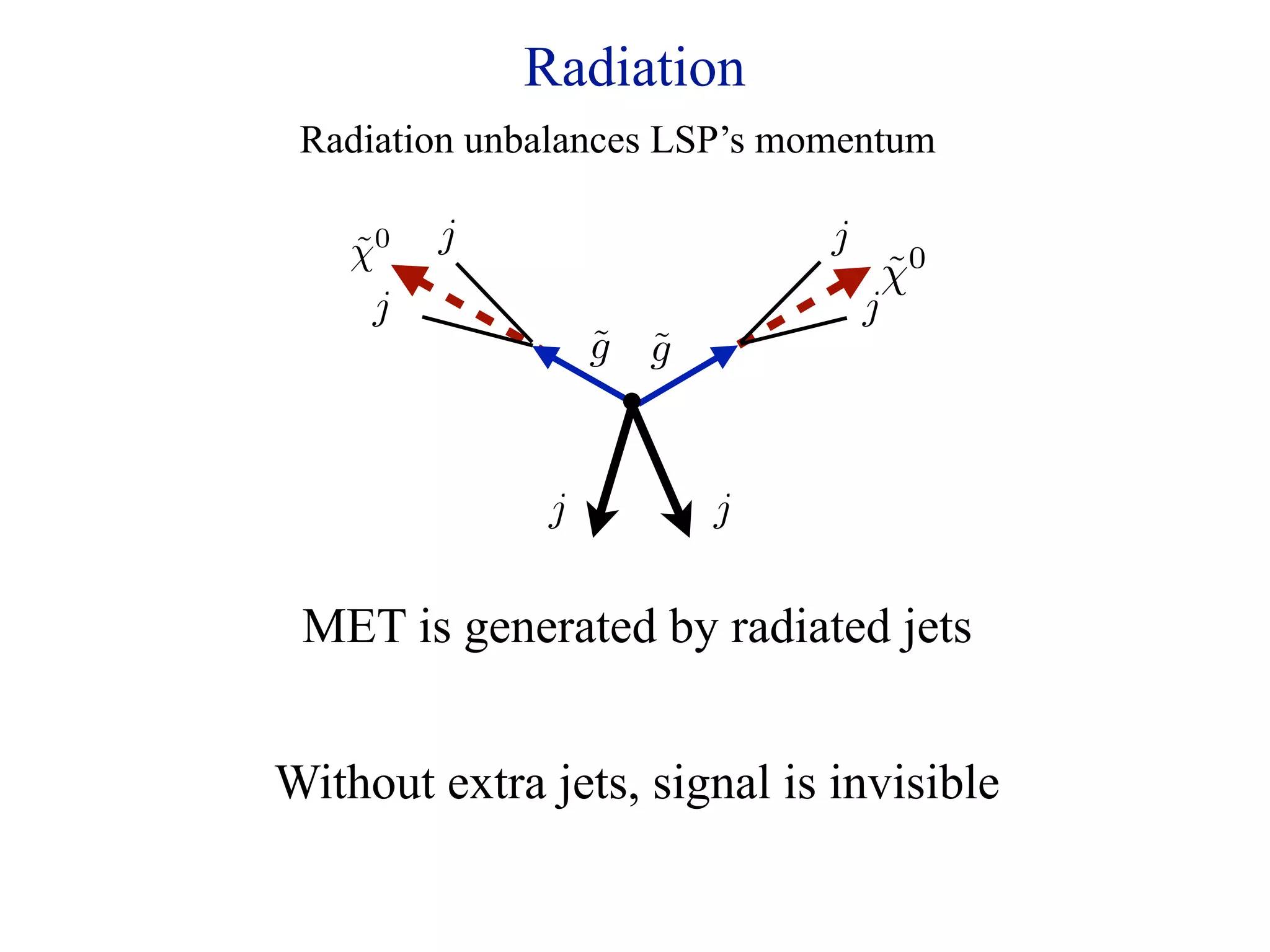
11. Radiation
Degenerate spectra require radiation to generate signal
V. GLUINO EXCLUSION LIMITS
A. No Cascade Decays
˜
mχ
For the remainder of the paper, we will discuss how model-independent jets + ET searches
can be used to set limits on the parameters in a particular theory. We will focus specifically
=
on the case of pair-produced gluinos at the Tevatron and begin by considering the simplified
scenario of a direct decay to the bino. The expected number of jets depends on the relative
mχ
mass difference between the gluino and bino. When the mass difference is small, the decay
jets are very soft and initial-state radiation is important; in this limit, the monojet search
˜
is best. When the mass difference is large, the decay jets are hard and well-defined, so
M
the multijet search is most effective. The dijet and threejet searches are important in the
transition between these two limits.
X
m
As an example, let us consider the model spectrum with a 340 GeV gluino decaying
directly into a 100 GeV bino. In this case, the gluino is heavy and its mass difference with
the bino is relatively large, so we expect the multijet search to be most effective. Table III
shows the differential cross section grids for the 1-4+ jet searches for this simulated signal
point. The colors indicate the significance of the signal over the limits presented in Table II;
the multijet search has the strongest excesses.
Previously [28], we obtained exclusion limits by optimizing the ET and HT cuts, which
involves simulating each mass point beforehand to determine which cuts are most appropri-
ate. This is effectively like dealing with a 1 × 1 grid, for which a 95% exclusion corresponds
150
Bino Mass GeV
···
100
˜
χ0 ˜
Out[27]=
50 X
g
mX
0
Gluino Mass GeV
100 200 300 400 500
FIG. 4: The 95% exclusion region for DO at 4 fb−1 assuming 50% systematic error on background.
The exclusion region for a directly decaying gluino is shown in light blue; the worst case scenario
for the cascade decay is shown in dark blue. The dashed line represents the CMSSM points and
the “X” is the current DO exclusion limit at 2 fb−1 .
15
UED-like Theories
Unbalanced momentum set by Q = mg − mχ
˜ ˜
j ˜
g j
˜
χ0 ˜
χ0
j ˜
g j
As pT of gluino increases,
Final state jets get harder (and eventually merge),
but won’t gain significant MET

12. Radiation
Radiation unbalances LSP’s momentum
˜
χ0 j j
˜
χ0
j j
˜ ˜
g g
j j
MET is generated by radiated jets
Without extra jets, signal is invisible

13. Spectrum of Radiation Harder for New Physics
When LSP is heavy sS sBG
(rest mass of LSP is unobservable)
Cross section for background is large due to lower SM CM energy

14. Spectrum of Radiation Harder for New Physics
Consider the additional cost of energy for radiating a jet
off a particle, X, of mass m
pµ = (Ej , Ej )
j pµ
X = m2 + Ej , −Ej
2
√ Ej m Ej
δ s(Ej ) = Ej + m2 + E2 − m =
j
2Ej m Ej
√
Identify m→ s

15. Spectrum of Radiation Harder for New Physics
When LSP is heavy sS sBG
(rest mass of LSP is unobservable)
Cross section for background is large due to lower SM CM energy
√
Radiate off a jet with Ej ∼ sS
√
√ Ej Ej s
δ s(Ej ) = √
2Ej Ej s
√ √ √ √
sS+j sS + Ej sBG+j sBG + 2Ej
sS+j sBG+j
Equalizes CM energy for signal and background
Increases S/B significantly
Works because we’re beyond last SM threshold at the LHC

16. An Example
mg = 250 GeV
˜ mχ0 = 200 GeV
˜
√
2000 s = 14 TeV
1000
(fb/25 GeV)
500
High MET cut doesn’t kill signal
200
100 Matched
dET
50
Unmatched
dσ
20
10
0 200 400 600 800 1000
ET (GeV)
Tail is enhance by a factor of 10!

17. Plan of Talk
Distinguishing Signal from Background
* Where the LHC can get to (soon)

18. Multijet Universality
Selection Criteria for Different Jet Multiplicity Searches
1j + ET
2j + ET
3j + ET 4+ j + ET
j1 ≥ 400 GeV ≥ 100 GeV ≥ 100 GeV ≥ 100 GeV
j2 50 GeV ≥ 50 GeV ≥ 50 GeV ≥ 50 GeV
j3 50 GeV 50 GeV ≥ 50 GeV ≥ 50 GeV
j4 50 GeV 50 GeV 50 GeV ≥ 50 GeV
Table 1: The selection criteria for the different jets plus missing energy samples. Jet pT cuts
in GeV for the different exclusive search channels. The following cuts are applied: |ηj | 2.5,
Never20 GeV, ∆φ(ET , ji) jet multiplicity to significantly enhance discovery
pT, found lower 0.2 rad. (i = 1, 2, 3).
Degenerate spectra
2.1 Classification of Search Channels
Light Squarks, Heavy Gluinos
Discovering new physics in an all-hadronic final state is a challenging prospect in the jet-
rich environment of the LHC. The QCD and instrumental backgrounds, particularly in
early running, are a major challenge. In shape variables and ensure that the events
Tried many different event order to both trigger and search strategies
are sufficiently distinctive compared to poorly understood backgrounds, the searches
considered in this article have tighter cuts than the ones considered in the published
search strategies from ATLAS and CMS. For instance, thethe Tevatron article were
Qualitatively different than cuts used in this
initially based on the benchmark ATLAS multijet + ET searches [3]. This article finds
that requiring a larger missing energy criteria is more effective at separating signal from
background
The first step in devising a model-independent, inclusive search strategy is to clas-

19. 14 TeV

20. 3 Searches
900 GeV
HT
High MET ET 600 GeV
1200 GeV
Gluinos, Squarks Degenerate Spectra

600 GeV

Alpha E T 400 GeV α 0.20 HT 900 GeV


1200 GeV
Gluinos, Squarks

600 GeV

Mid MET E T 400 GeV HT 900 GeV


1200 GeV
Cascade Decays

21. The Searches
pp → g g + X → (q q χ0 )(q q χ0 ) + X
˜˜ ¯˜ ¯˜
High MET Search
ET 600 GeV
HT 900 GeV, 1200 GeV
600
500
400
Bino Mass GeV
300
200
100
0
Gluino Mass GeV
200 400 600 800 1000

22. ariables, the sensitivity in multijet and ET searches will
ent shape variable, αRTS Alphaintroduced in [24]. αRTS was
The , first Variable
Introduced by L. Randall D. Tucker-Smith
pT j2 pT j2
α
αRTS =
mj1 j2
pT j1 (1 − cos θj1j2 )
are the transverse momentumto multijet leading two jets in t
Modified by CMS
of the searches
ant mass between the3 leading and subleading jets, and θj
j
j1
m. αRTS was introduced as an alternative to ET in eli
in dijet + ET searches; j2evaluating Eq. 2.3 for a topology
Group to minimize
al QCD scenario, gives αRT S = 0.5. Fig. 2 shows a αRTS
momentum imbalance
QCD sample and the electroweak 1 SM backgrounds with2
j Sj
hape suggests applying a cut αRTS ≥ 0.55 as an alternati
d ET searches. However, the region below 0.5 is where new

23. Discovery Reach
Alpha Search
E T 400 GeV HT 600 GeV, 900 GeV, 1200 GeV
α 0.20
Directly decaying gluinos Directly decaying Squarks
pp → g g + X → (q q χ0 )(q q χ0 ) + X
˜˜ ¯˜ ¯˜ pp → q q + X → (q χ0 )(¯χ0 ) + X
˜˜ ˜ q˜
600 400
500
300
Bino Mass GeV
400
Bino Mass GeV
Alpha
300 200
High MET High MET Alpha
200
100
100
0
Gluino Mass GeV
200 400 600 800 1000 0
Squark Mass GeV
100 200 300 400 500 600
Multijet still more effective than dijets

24. Cascade Decays
˜ ¯
g → qqχ 0
→ q q (q q χ )
¯ ¯ 0
Lowers MET in Events
Mid MET Search
E T 400 GeV HT 600 GeV, 900 GeV, 1200 GeV
500
High MET
400
Bino Mass GeV
300 Mid MET
200
100
Alpha
0
Gluino Mass GeV
200 400 600 800

25. Extended Cascade Decays
g → q q χ → (q q )q q χ → (q q )(q q )q q χ
˜ ¯
¯ ¯
¯ ¯ ¯
LSP is great-granddaughter
Momentum is divided many different ways
Reduces MET dramatically
Need a low MET search E T 200 GeV
Worse case scenario
˜
g 400 GeV
χ 200 GeV
χ 100 GeV
χ 50 GeV

26. 7 TeV
(in progress)
Interpolating from Tevatron to 14TeV LHC
High MET ET 400 GeV
Alpha ET 300 GeV
α 0.2

27. Direct Gluino Decays
pp → g g + X → (q q χ0 )(q q χ0 ) + X
V.
˜˜ ¯˜ ¯˜
GLUINO EXCLUSION LIMITS
A. No Cascade Decays
For the remainder of the paper, we will discuss how model-independent jets + ET searches
can be used to set limits on the parameters in a particular theory. We will focus specifically
on the case of pair-produced gluinos at the Tevatron and begin by considering the simplified
400
scenario of a direct decay to the bino. The expected number of jets depends on the relative
mass difference between the gluino and bino. When the mass difference is small, the decay
jets are very soft and initial-state radiation is important; in this limit, the monojet search
is best. When the mass difference is large, the decay jets are hard and well-defined, so
the multijet search is most effective. The dijet and threejet searches are important in the
transition between these two limits.
As an example, let us consider the model spectrum with a 340 GeV gluino decaying
300
directly into a 100 GeV bino. In this case, the gluino is heavy and its mass difference with
the bino is relatively large, so we expect the multijet search to be most effective. Table III
shows the differential cross section grids for the 1-4+ jet searches for this simulated signal
Bino Mass GeV
point. The colors indicate the significance of the signal over the limits presented in Table II;
the multijet search has the strongest excesses.
Previously [28], we obtained exclusion limits by optimizing the ET and HT cuts, which
involves simulating each mass point beforehand to determine which cuts are most appropri-
200
ate. This is effectively like dealing with a 1 × 1 grid, for which a 95% exclusion corresponds
150
Bino Mass GeV
100
100
2σ
Out[27]=
50
00
X
5σ
Gluino Mass GeV
Gluino Mass GeV
100
200
200 300
400
400 500
600 800
FIG. 4: The 95% exclusion region for DO at 4 fb−1 assuming 50% systematic error on background.
The exclusion region for a directly decaying gluino is shown in light blue; the worst case scenario
for the cascade decay is shown in dark blue. The dashed line represents the CMSSM points and
the “X” is the current DO exclusion limit at 2 fb−1 .
15
Doubling the reach in the next year!

28. Conclusion

29. Conclusion
Discovery at the LHC in Jets + MET much easier
than at the Tevatron
Matching gets the features of the signal right
and makes it more visible
Simple search strategies will provide
extensive coverage