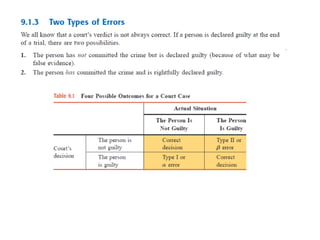
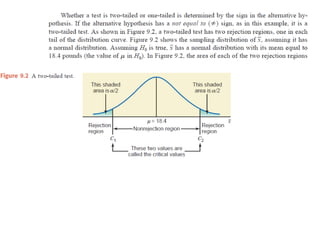
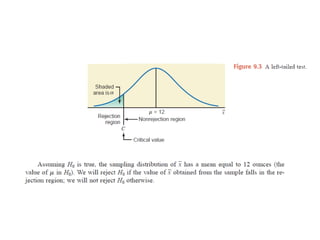
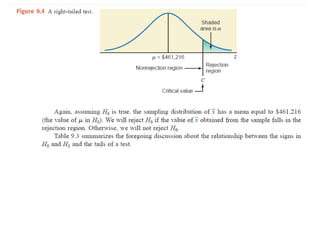
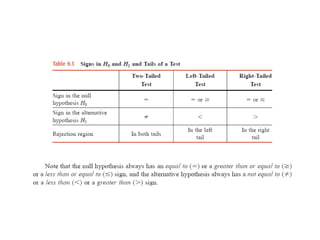
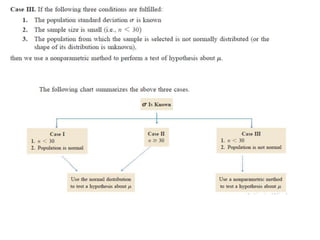
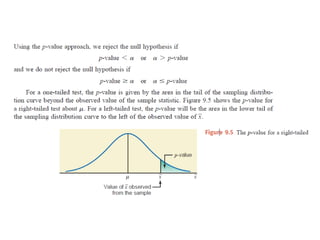
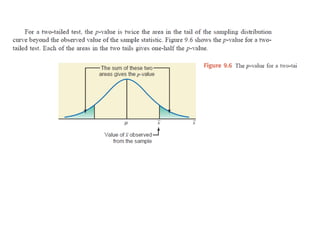
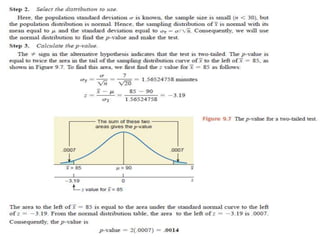
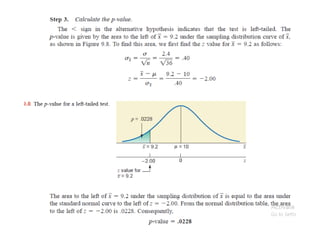
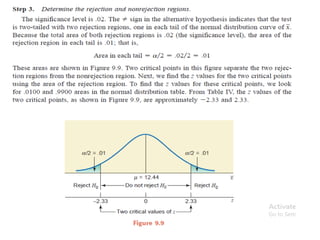
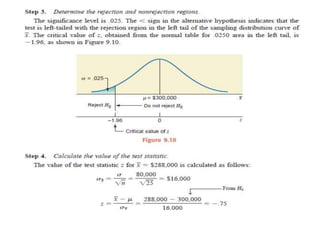
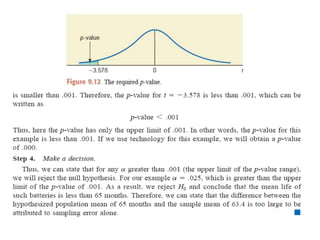
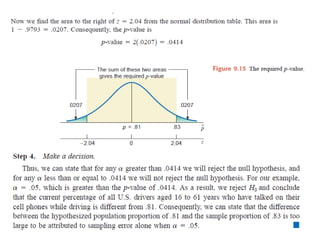
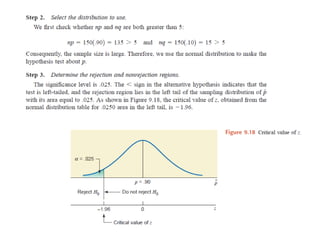
The document discusses the null hypothesis and how it is used to test claims about population parameters. Specifically, it gives an example of testing a soft drink company's claim that its cans contain 12 ounces on average. The null hypothesis would be that the company's claim is true. To test this, the procedure involves determining the critical value from the normal distribution table based on the significance level, finding the test statistic value, and comparing the two to make a decision about rejecting or failing to reject the null hypothesis.

3. The null hypothesis states that a given claim (or statement) about a population
parameter is true.

4. Reconsider the example of the soft-drink company’s claim that, on average, its cans contain 12
ounces of soda.
• In reality, this claim may or may not be true.
• However, we will initially assume that the company’s claim is true (that is, the
company is not guilty of cheating and lying).
• To test the claim of the soft-drink company, the null hypothesis will be that the
company’s claim is true.

18. Home Work

32. Critical Value Approach
• In this procedure, we have a predetermined value of the significance level ∝.
•
i. The value of ∝ gives the total area of rejection regions.
ii. First we find the critical value(s) of z from the normal distribution table for the
given significance level.
iii. Then we find the value of the test statistic z for the observed value of the sample
statistic 𝑥.
iv. Finally we compare these two values and make a decision.
• Remember, if the test is one-tailed, there is only one critical value of z, and it
is obtained by using the value of ∝ which gives the area in the left or right
tail of the normal distribution curve depending on whether the test is left-
tailed or right-tailed, respectively.
• However, if the test is two-tailed, there are two critical values of z and they
are obtained by using
∝
2
area in each tail of the normal distribution curve.

58. Any Question??