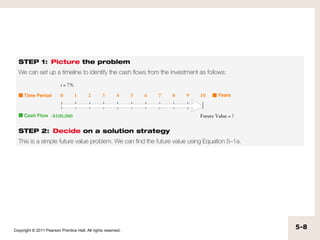
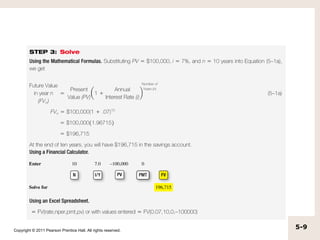
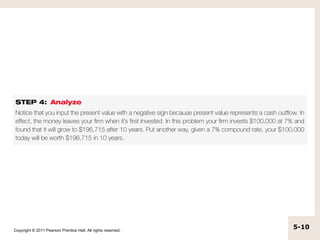
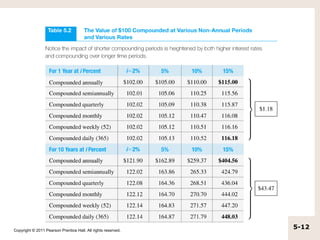
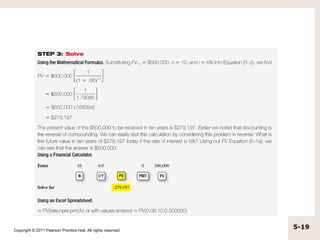
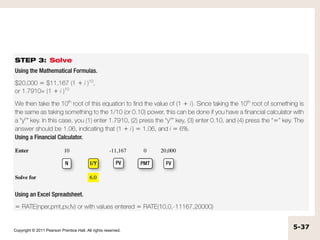
The document discusses simple interest versus compound interest. Simple interest is earned only on the principal amount, while compound interest is earned on both the principal and accumulated interest of prior periods. An example shows that with a $500 principal, 5% annual interest rate, compound interest results in a higher balance ($551.25) after two years compared to simple interest ($550). The document also covers topics like present value, future value, using calculators and formulas to solve for unknown time periods, interest rates, and cash flow amounts.






























![Comparing Loans using EAR (cont.)
• Example 5.9 Calculate the EAR for a loan
that has a 5.45% quoted annual interest
rate compounded monthly.
• EAR = [1+.0545/12]12 - 1
=
1.0558 – 1
= .05588 or 5.59%
Copyright © 2011 Pearson Prentice Hall. All rights reserved.
5-41](https://image.slidesharecdn.com/chapter5interest-130320131416-phpapp01/85/Chapter-5-interest-41-320.jpg)

