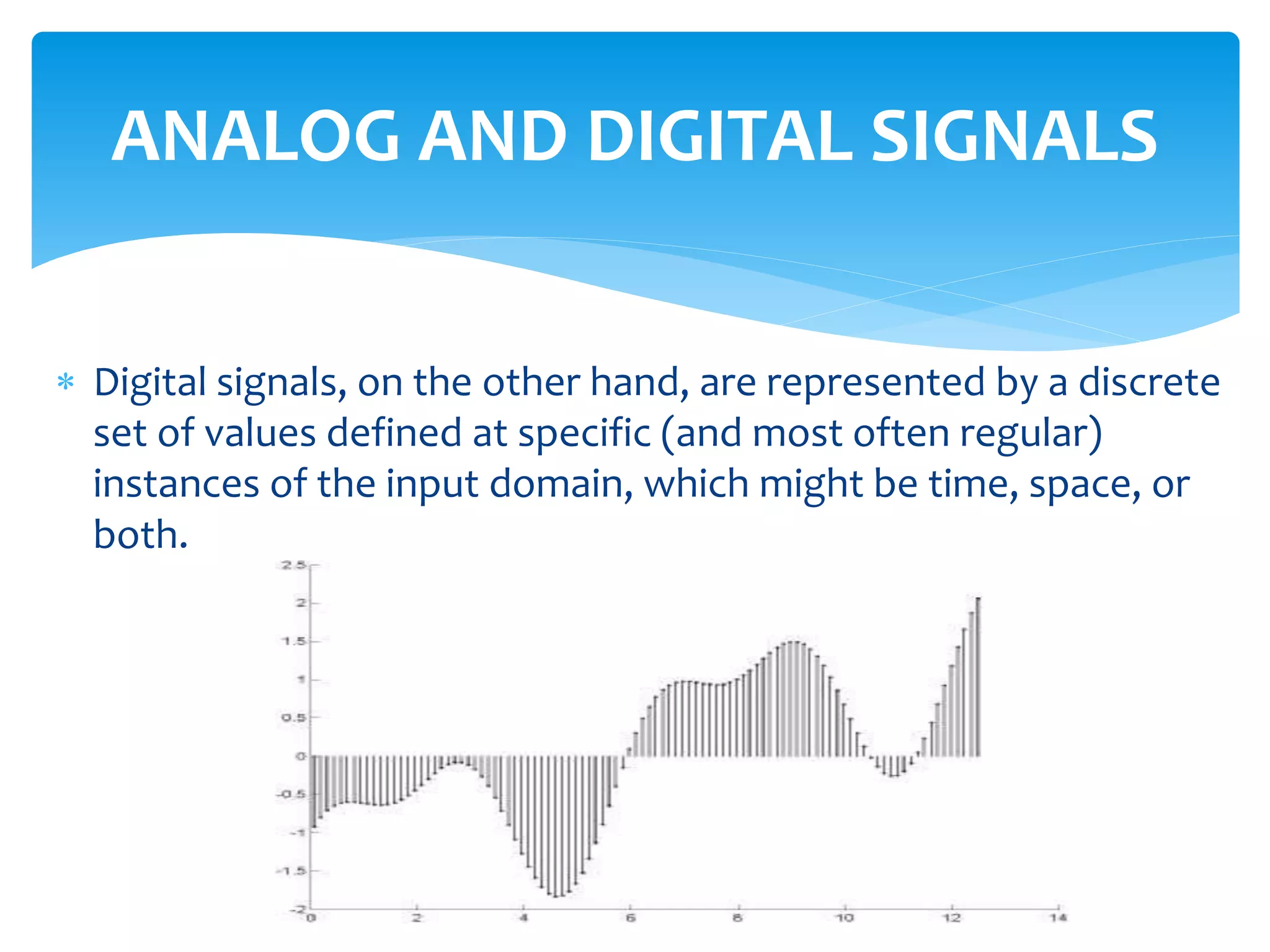
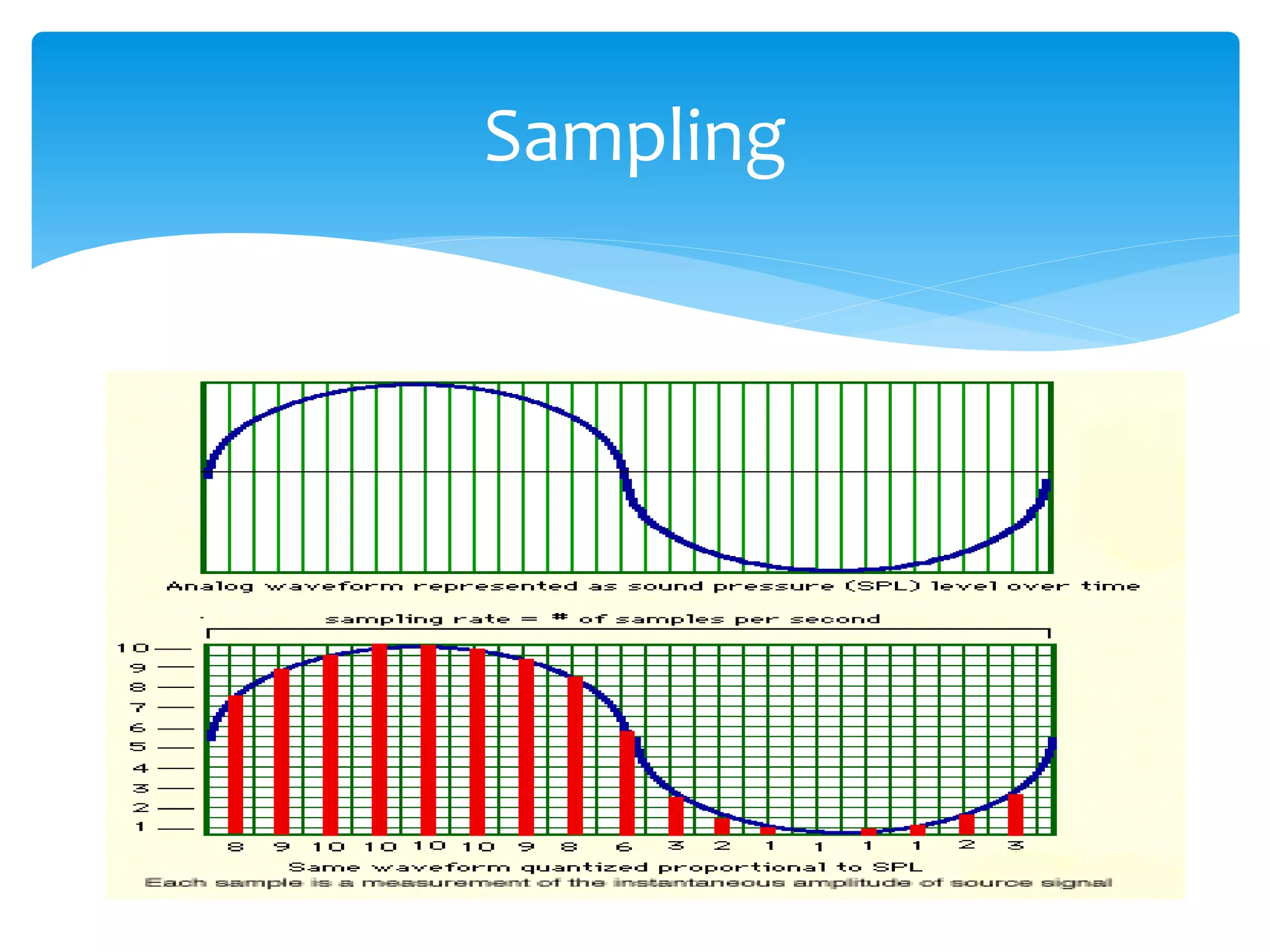
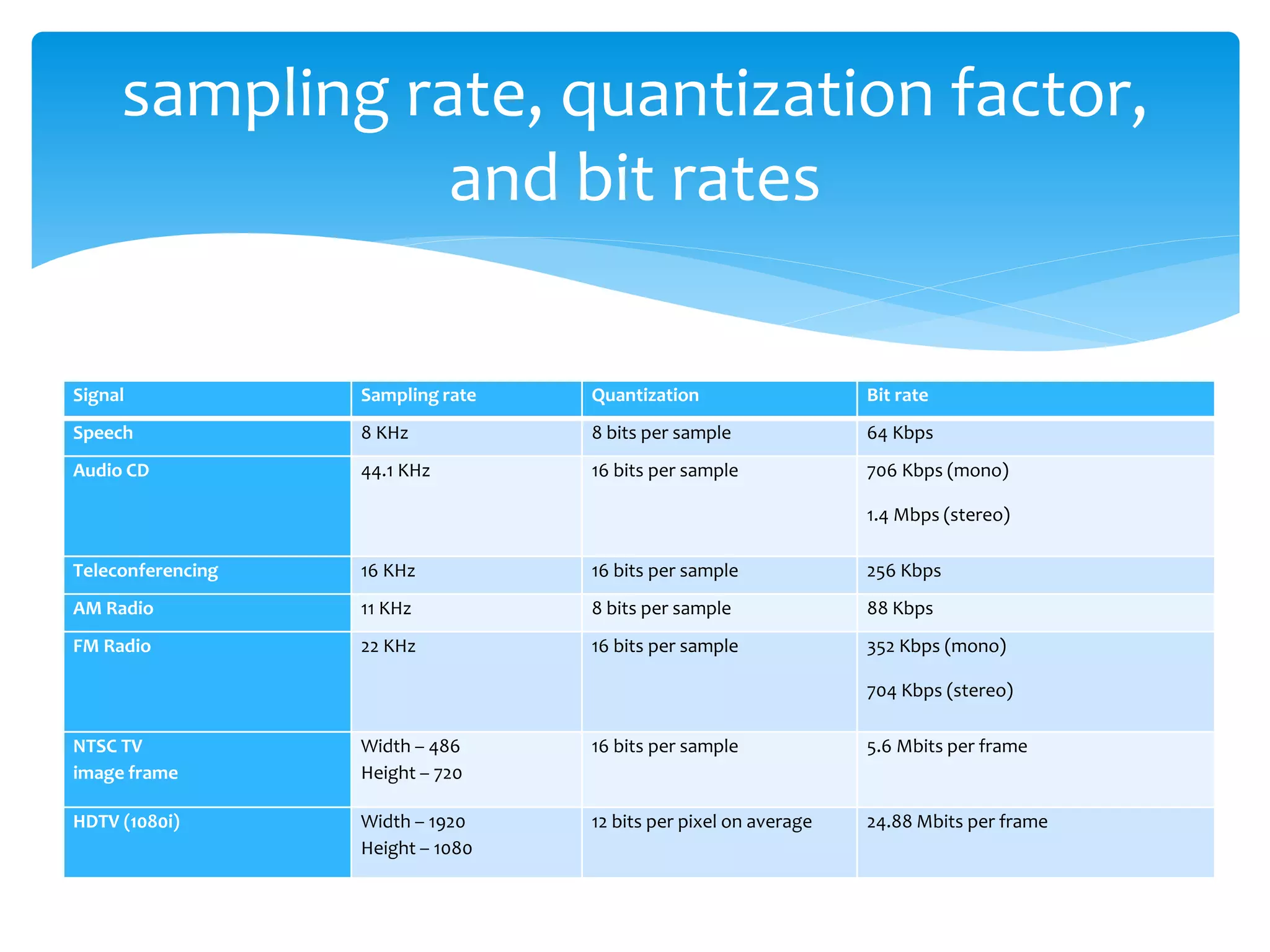
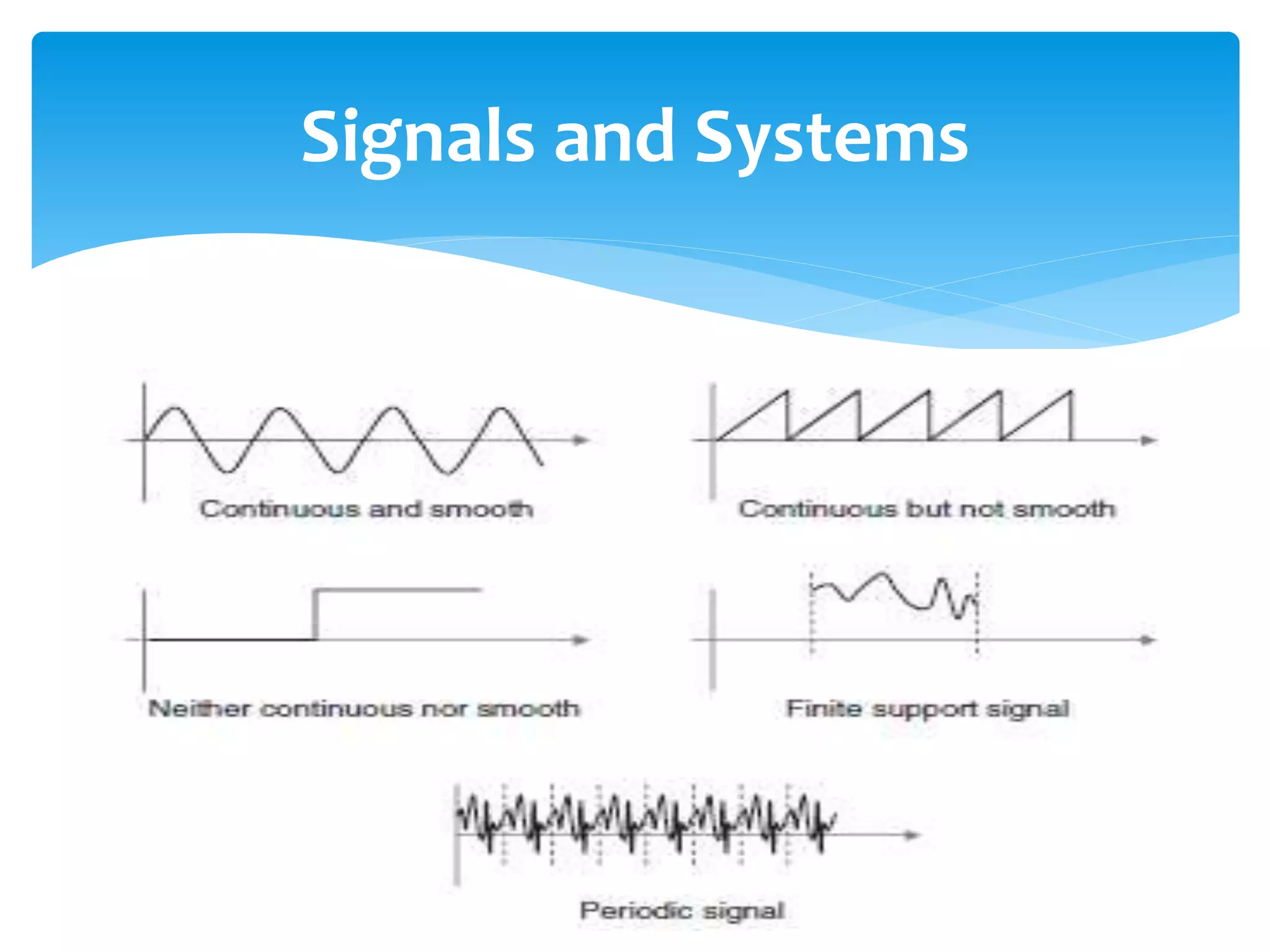
This chapter describes the process of converting analog signals to digital form. It discusses sampling, where the analog signal is captured at discrete time intervals. It also discusses quantization, where the amplitude of the signal at each sample is assigned a digital value. The sampling rate and number of quantization levels affect the quality and size of the digital data. Digital signals have advantages over analog like improved quality, ability to edit and combine content, and efficient compression and storage. The chapter also covers filtering of digital signals.

1. Chapter 2
Digital Data Acquisition
Course Teacher: Shahid Hussain

2.  One of the first task is content creation into digital form
 Making it easy to combine, and assemble heterogeneous media
entities
 This chapter describes the theoretical foundations underpinning
the conversion and recording of information into a digital
medium.
 Process of conversion analog to digital related to the two
conditions
 Quality of digital data
 Quantity of digital data
 Both are important for creation and distribution of multimedia
Introduction

3.  Analog signals are captured by a recording device, which
attempts to record a physical signal. A signal is analog if it can be
represented by a continuous function. For instance, it might
encode the changing amplitude with respect to an input
dimension(s).
ANALOG AND DIGITAL SIGNALS

4.  Digital signals, on the other hand, are represented by a discrete
set of values defined at specific (and most often regular)
instances of the input domain, which might be time, space, or
both.
ANALOG AND DIGITAL SIGNALS

5.  When media is represented digitally, it is possible to create
complex, interactive content. In the digital medium, we can
access each unit of information for a media type, for example,
it is easy to access a pixel in an image, or a group of pixels in a
region or even a section of a sound track. Different digital
operations can be applied to each, such as to enhance the
image quality of a region, or to remove noise in a sound track.
Also, different digital media types can be combined or
composited to create richer content, which is not easy in the
analog medium.
Advantages of Digital Signals over
Analog Signals

6.  Stored digital signals do not degrade over time or distance as
analog signals do. One of the most common artifacts of
broadcast VHS video is ghosting, as stored VHS tapes lose their
image quality by repeated usage and degradation of the
medium over time. This is not the case with digital
broadcasting or digitally stored media types.
 Digital data can be efficiently compressed and transmitted
across digital networks. This includes active and live
distribution models, such as digital cable, video on demand,
and passive distribution schemes, such as video on a DVD.
Advantages of Digital Signals over
Analog Signals

7.  It is easy to store digital data on magnetic media such as
portable 3.5 inch, hard drives, or solid state memory devices,
such as flash drives, memory cards, and so on. This is because
the representation of digital data, whether audio, image, or
video, is a set of binary values, regardless of data type.
 Digital data is preferred because it offers better quality and
higher fidelity, can be easily used to create compelling content,
and can also be compressed, distributed, stored, and retrieved
relatively easily.
Advantages of Digital Signals over
Analog Signals

8.  The conversion of signals from analog to digital
occurs via two main processes: sampling and
quantization. The reverse process of converting
digital signals to analog is known as interpolation.
One of the most desirable properties in the analog to
digital conversion is to ensure that no artifacts are
created in the digital data. That way, when the signal
is converted back to the analog domain, it will look
the same as the original analog signal.
ANALOG to DIGITAL conversion

9.  For analog to digital conversion the original waveform is broken
into individual snapshots called samples. These samples are
measured using continuous intervals.
 The rate at which continuous waveform is sampled called
sampling rate.
 If the number of samples increase (increase f, reduce T)
correspondingly the data storage requirements increase while it
offer better quality during regeneration of signals.
 Vice versa if T is increased and f is decreased the storage
requirements will become less while it degrades the signal
quality.
Sampling

10. Sampling

11.  Quantization deals with encoding the signal value at every
sampled location with a predefined precision, defined by a
number of levels.
 Because each sample is represented by a finite number of
bits, the quantized value will differ from the actual signal
value, thus always introducing an error.
 The maximum error is limited to half the quantization step.
The error decreases as the number of bits used to
represent the sample increases.
Quantization

12.  How many bits should be used to represent each
sample?
 Is this number the same for all signals?
 This actually depends on the type of signal and what
its intended use is.
 Audio signals, which represent music, must be
quantized on 16 bits, whereas speech only requires 8
bits.
Quantization

13. Quantization

14. Quantization
 Figure illustrates quantization
effects in two dimensions for
images.
 The results show that the
error increases as the number
of quantization bits used to
represent the pixel samples
decreases.

15.  Number of bits produced per second is called as bit
rate.
 Bit rate is critical when it come to digital signal
storage or transmitting across the network.
 Measured in terms of bits per second
Bit Rate

16. Signal Sampling rate Quantization Bit rate
Speech 8 KHz 8 bits per sample 64 Kbps
Audio CD 44.1 KHz 16 bits per sample 706 Kbps (mono)
1.4 Mbps (stereo)
Teleconferencing 16 KHz 16 bits per sample 256 Kbps
AM Radio 11 KHz 8 bits per sample 88 Kbps
FM Radio 22 KHz 16 bits per sample 352 Kbps (mono)
704 Kbps (stereo)
NTSC TV
image frame
Width – 486
Height – 720
16 bits per sample 5.6 Mbits per frame
HDTV (1080i) Width – 1920
Height – 1080
12 bits per pixel on average 24.88 Mbits per frame
sampling rate, quantization factor,
and bit rates

17.  A practical categorization of the signals can be viewed as
follows:
1. Continuous and smooth – Such as a sinusold
2. Continuous but not smooth—Such as a saw tooth.
3. Neither smooth nor continuous—For example, a step edge.
4. Symmetric—Which can be further described either as odd (y
= sin(x)) or even (y = cos(x)). Note that any signal can be
decomposed into the sum of an odd and even part.
Signals and Systems

18. 5. Finite support signals—Signals that are defined for a
finite interval and zero outside of that interval.
6. Periodic signal—A signal that repeats itself over a time
period. For a periodic signal f(x), the period is defined to
be T if f (x + T) = f (x). For any function f (t), we can
define a periodic version of f (t), g(t) = ∑k f (t kT).
Signals and Systems

19. Signals and Systems

20.  Relationship between signals and sampling was established by
Henry Nyquist in late 1920s.
 Later formalized by Claud Shanon in 1950.
 Relationship say that:
 Signal has to be sampled at least twice of the signal maximum
frequency.
 fs >= 2 * fmax
 Where fs is sampling rate, fmax is maximum signal frequency
Note:
Refer the book and notebook to find examples on this algorithm.
Sampling Theorem and Aliasing

21.  What happens if your sampling frequency is higher
than Nyquist theorem
 Nothing special
 During reproducing signal you will find all necessary
information
 You will generate more digital data and increase the cost
over head on storage and transmission
Sampling Theorem and Aliasing

22.  What happens if your sampling frequency is less than
Nyquist theoram
 It cause a problem
 Reproduced signal will not have the complete
information as original analog signal
 Result is artifacts which is termed as Aliasing
 Aliasing is a term used to defined the loss during
digitization
Sampling Theorem and Aliasing

23. a) Aliasing in spatial domain
 Can be one dimensional or two dimensional
 Can be observed in high frequency areas
 Fan blades
b) Aliasing in temporal domain
c) Moire patterns and aliasing
Sampling Theorem and Aliasing

24.  In signal processing filter is used to:
 Remove unwanted parts of the signal, such as random
noise and undesired frequencies
 Extract useful parts of the signal such as components
lying within a certain frequency range.
 Can be categorized into two:
 Analog filter
 Digital filter
Filtering

25.  Analog filters use electronic circuits made up from
components such as registers, capacitors, and
operational amplifiers to produce the required
filtering effect.
 Such filter circuits are widely used in application such
as:
 Noise reduction
 Video signal enhancement
 Graphic equalizer in hi fi systems and etc.
Filtering

26.  Digital filter use digital numeric computations on
sampled quantized value of the signal.
 Processing can be done on:
 General purpose PC or
 Specialized Digital Signal Processor (DSP) chip
 Digital filters has many advantage over analog filter
Filtering

27. 1. A digital filter is programmable, that is, a program stored
in the processor’s memory determines its operation. This
means the digital filter can easily be changed without
affecting the circuitry (hardware). An analog filter can
only be changed by redesigning the filter circuit.
2. Digital filters are easily designed, tested, and
implemented on a general-purpose computer or
workstation.
3. Digital filters can be combined in parallel or cascaded in
series with relative ease by imposing minimal software
requirements. That is not the case with analog circuitry.
Filtering

28. 4. The characteristics of analog filter circuits (particularly
those containing active components) are subject to drift
and are dependent on temperature. Digital filters do not
suffer from these problems, and so are extremely stable
with respect both to time and temperature.
5. Unlike their analog counterparts, digital filters can handle
low-frequency signals accurately. As the speed of DSP
technology continues to increase, digital filters are being
applied to high-frequency signals in the RF (radio
frequency) domain, which in the past was the exclusive
preserve of analog technology.
Filtering

29. 6. Digital filters are more versatile in their ability to
process signals in a variety of ways; this includes the
ability of some types of digital filter to adapt to
changes in the characteristics of the signal.
 Both analog and digital filters can be divided into
three categories.
 Low pass filter
 Band pass filter
 High pass filter
Filtering

30.  Low pass filters remove high frequency content from
the input signals
 Used for aliasing artifacts during sampling
 High pass filters removes low frequency contents
 Used to enhance edges and sharpen the image
 Band pass filters contains the frequency belonging to
a defined band
 Other components are filtering in 1D, filtering in 2D
Filtering