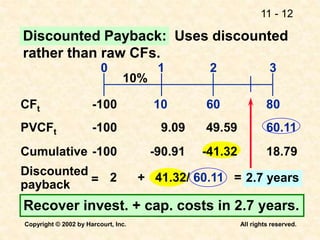
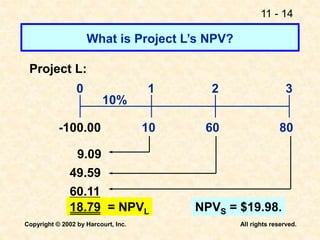
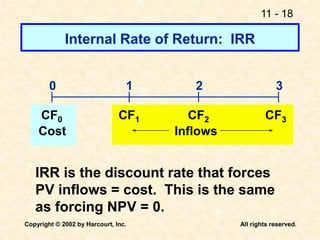
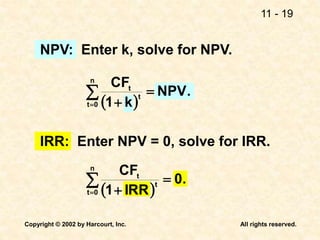
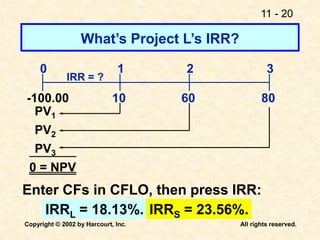
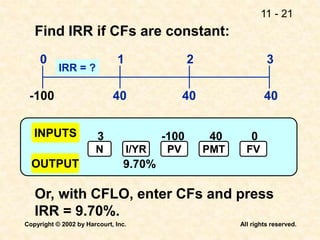
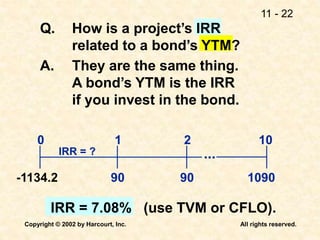
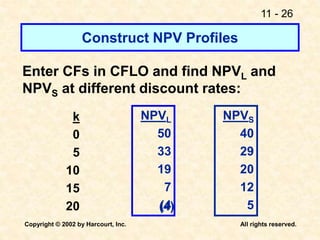
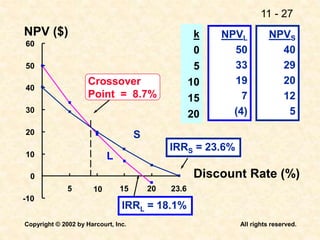
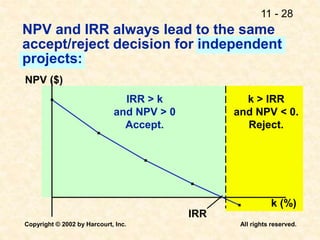
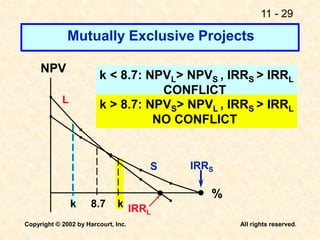
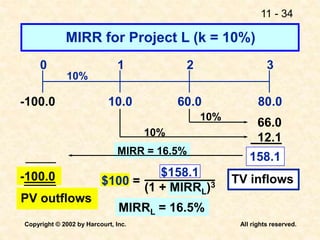
This document discusses capital budgeting and the key concepts involved. It defines capital budgeting as the analysis of potential additions to fixed assets involving large long-term expenditures that are important to a firm's future. The document outlines the steps in capital budgeting as estimating cash flows, assessing risk, determining the weighted average cost of capital, and using net present value or internal rate of return methods. It also discusses the differences between independent and mutually exclusive projects and provides examples to illustrate capital budgeting methods and decisions.