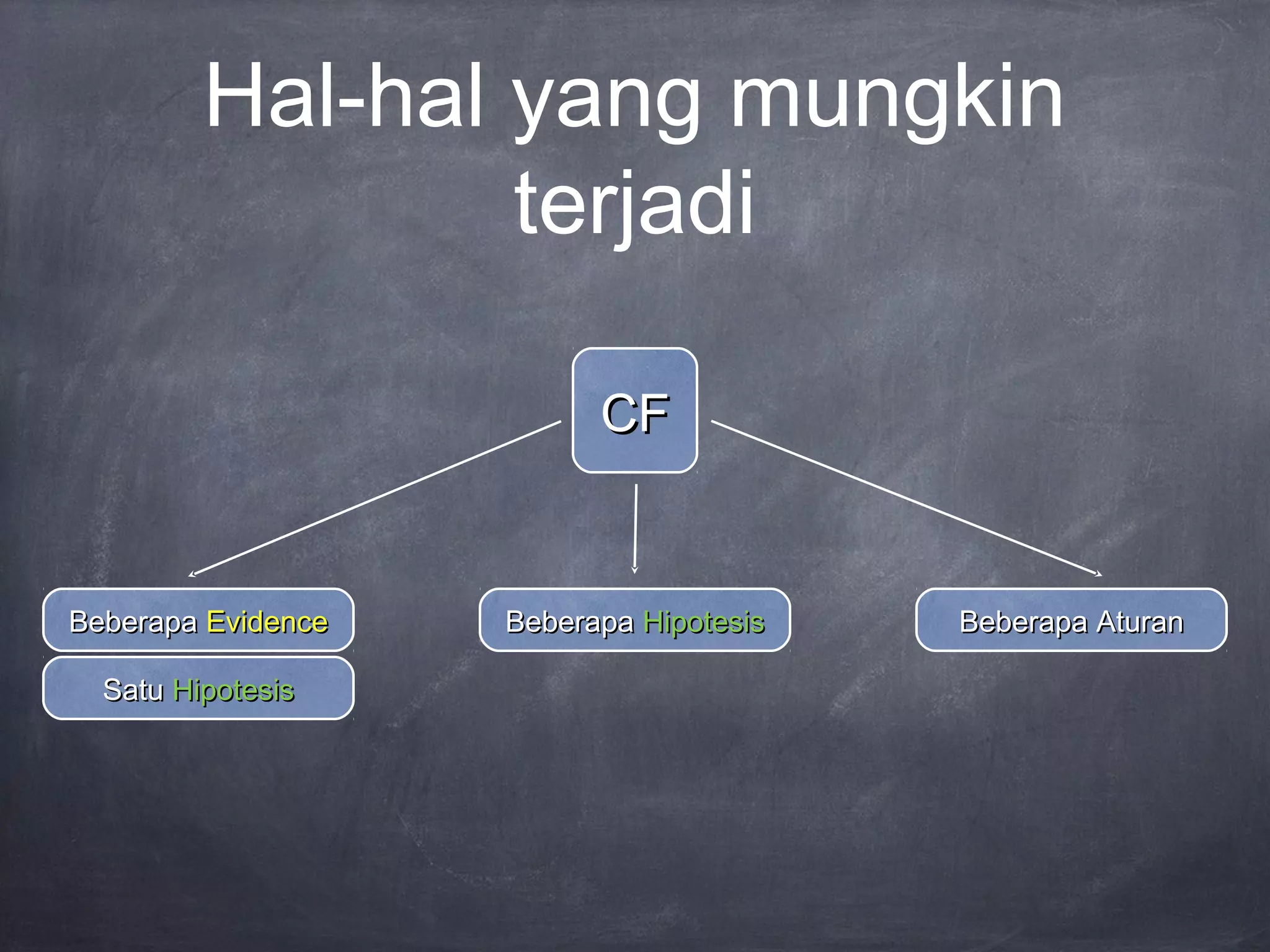
Teori Faktor Kepastian menggunakan nilai faktor kepastian (CF) untuk mengekspresikan keakuratan sebuah hipotesis berdasarkan bukti yang ada. CF dihitung dari selisih antara ukuran kepercayaan dan ketidakpercayaan terhadap suatu hipotesis, dengan nilai berkisar antara -1 hingga 1. Teori ini dapat menggabungkan pendapat dari beberapa pakar dan mempertimbangkan adanya beberapa bukti maup

1. Certainty Factor Theory
Rachmat Wahid Saleh Insani

2. Pengertian
Faktor Kepastian digunakan untuk mengekspresikan ke-akurat-an,
kebenaran atau kehandalan sebuah pertimbangan
Diukur berdasarkan perbedaan antara ukuran kepercayaan dengan
ukuran ketidakpercayaan di sebuah hipotesa dari fakta yang ada
Singkatan yang digunakan:
CF (Certainty Factor)
H (Hypothesis)
E (Evidence)
MB (Measures of Belief)
MD (Measures of Disbelief)

3. Pengertian
Hipotesis disimbolkan dengan H
Nilai H berada dalam range -1 hingga 1
-1 artinya menyangkal hipotesa H
+1 artinya mengakui hipotesa H
Hipotesis memiliki peringkat
CF Ditentukan berdasarkan 2 hal:
MB, measures of belief (percaya bahwa H true)
MD, measures of disbelief (percaya bahwa H false)
MB ≠ 1-MD

4. Aturan Dasar
CF(H|E), dibaca “CF dari hipotesis H dari fakta E”, dihitung dengan rumus
CF(H|E) = MB(H|E) – MD(H|E)
-1 ≤ CF(H) ≤ +1
MB(H|E), kepercayaan bahwa benar hipotesa H dari fakta E
MD(H|E), kepercayaan bahwa salah hipotesa H dari fakta E
CF dapat berintegrasi dengan pemikiran pakar yang berbeda-beda
Nilai CF untuk H menggunakan CF dari premis P di sebuah rule, adalah
CF(H) = CF(P1 dan P2) = min (CF(P1),CF(P2))
CF(H) = CF(P1 atauP2) = max (CF(P1),CF(P2))

5. Hal-hal yang mungkin
terjadi
CFCF
BeberapaBeberapa EvidenceEvidence
SatuSatu HipotesisHipotesis
BeberapaBeberapa HipotesisHipotesis Beberapa AturanBeberapa Aturan

6. CF dari Beberapa Evidence, Satu
Hipotesis
MB(H|E1 ∧ H|E2) hasilnya
0 jika MD(H|E ∧ H|E3) = 1, atau dihitung
MB(H|E1) + MB(H|E2) * (1 - MB(H|E1))
MD(H|E1 ∧ H|E2) hasilnya
0 jika MB(H|E1 ∧ H|E2) = 1, atau dihitung
MD(H|E1) + MD(H|E2) * (1 - MD(H|E1))

7. Contoh Soal (1)
Suatu observasi memberi kepercayaan pada h dengan MB(h|e1)=0.3 dan
MD(h|e1)=0
CF(h|e1) = 0.3 - 0 = 0.3
Ada observasi baru dengan MB(h|e2)=0.2 dan MD(h|e2)=0
Beberapa evidence untuk satu hipotesis
MB(H|E1) + MB(H|E2) * (1 - MB(H|E1))
MB(h|e1 ∧ h|e2) = 0.3 + 0.2 * (1 - 0.3) = 0.44
MD(h|e1 ∧ h|e2) = 0
CF(h|e1 ∧ h|e2) = MB(h|e1 ∧ h|e2) - MD(h|e1 ∧ h|e2) = 0.44 - 0 =
0.44

8. CF Dari Beberapa Hipotesis
MB (H1|E ∧ H2|E) = min (MB(H1|E), MB(H2|
E))
MD (H1|E ∧ H2|E) = min (MD(H1|E), MD(H2|
E))
MB (H1|E ∨ H2|E) = max (MB(H1|E), MB(H2|
E))
MD (H1|E ∨ H2|E) = max (MD(H1|E), MD(H2|
E))

9. Contoh Soal (2)
Suatu observasi memberi kepercayaan pada h1 dengan MB(h1|e)=0.5 dan MD(h1|e)=0.2.
Observasi tersebut juga memberi kepercayaan pada h2 dengan MB(h2|e)=0.8 dan MD(h2|e)=0.1.
CF dihitung dari beberapa hipotesis
CF(h1|e) = 0.5 - 0.2 - 0.3
CF(h2|e) = 0.8 - 0.1 = 0.7
Untuk mencari CF(h1^h2) didapatkan dari,
MB(h1|e ∧ h2|e) = min (0.5 ; 0.8) = 0.5
MD(h1|e ∧ h2|e) = min (0.2 ; 0.1) = 0.1
CF(h1|e ∧ h2|e) = 0.5 - 0.1 = 0.4
Untuk mencari CF(h1|e∨h2|e) diperoleh dari,
MB(h1|e ∨ h2|e) = max (0.5 ; 0.8) = 0.8
MB(h1|e ∨ h2|e) = max (0.2 ; 0.1) = 0.2
CF(h1|e ∨ h2|e) = 0.8 - 0.2 = 0.6

10. CF Untuk Kondisi/Rule yang Berbeda
Nilai CF untuk H dikombinasikan dari beberapa rule berbeda,
pakar dan sebagainya:
Jika CF1, CF2 > 0
Maka, CF(H) = CF1+CF2-CF1*CF2
Jika CF1, CF2 < 0
Maka, CF(H) = CF1+CF2+CF1*CF2
Jika tidak berada di 2 kondisi sebelumnya
Maka, CF(H) = CF1+CF2 / 1-min(|CF1|,|CF2|)
|CF1|, adalah nilai mutlak CF1

11. Beberapa Aturan Saling
Bergantung, Ketidakpastian aturan
adalah input aturan lain
MB(H|S) = MB’(H|S) * max (0, CF (S|E))
MB(H|S) adalah ukuran kepercayaan H berdasarkan keyakinan
penuh terhadap validitas S
Contoh:
If PHK then Pengangguran
IF Pengangguran then Gelandangan
CF(Pengangguran|PHK)=0.9
MB (Gelandangan|Pengangguran)=0.7
maka, MB(Gelandangan|Pengangguran) = 0.7 * 0.9 = 0.63

12. Karakteristik CF
Jika Pasti Benar, maka
Probabilitas P(H|E)=1
MB=1
CF=1
Jika Pasti Salah, maka
Probabilitas P(-H|E)=1
MD=1
CF=-1
Jika, Tidak Terbukti maka
Probabilitas P(H|E)=P(H)
Range di setiap nilai MB, MD,
CF adalah
MB
0 <= MB <= 1
MD
0 <= MD <= 1
CF
-1 <= CF <= +1