Uploaded byXiong Wang
CCCN Talk on Stable Chaos
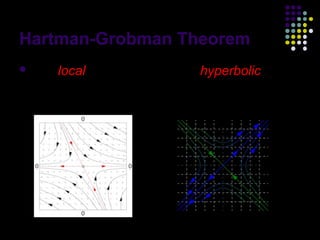
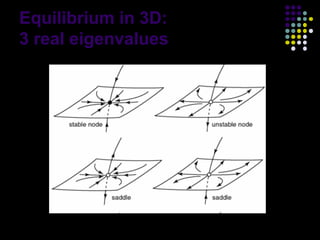
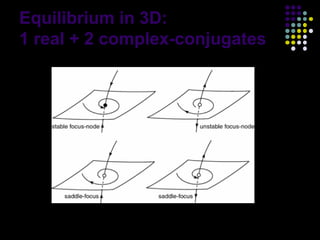
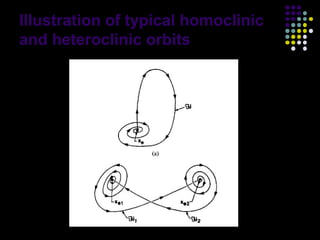
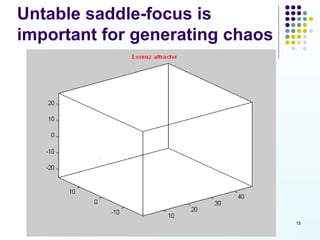
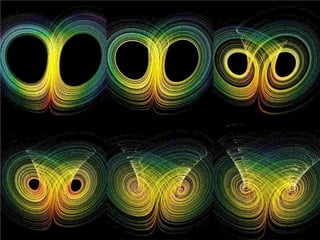
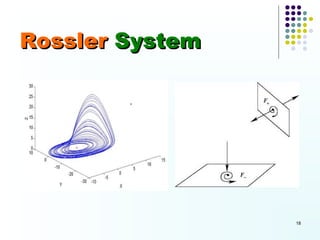
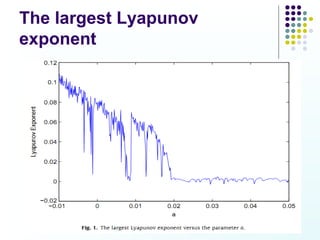
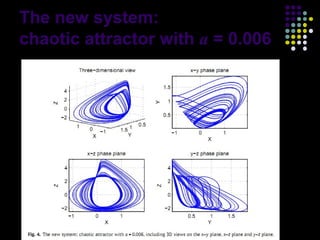
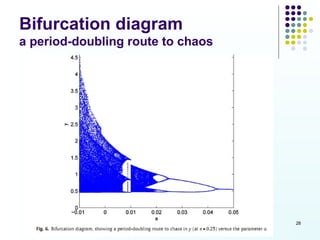
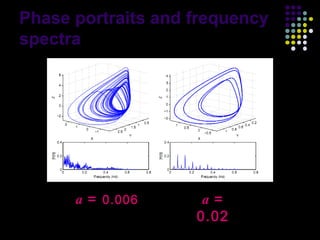
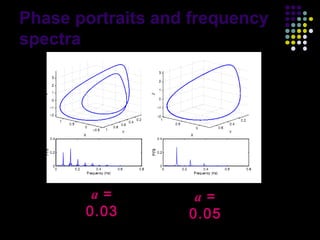
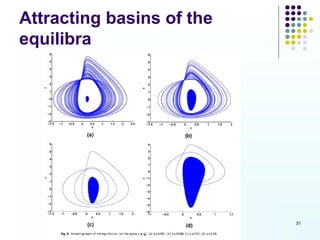
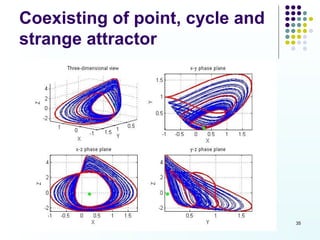
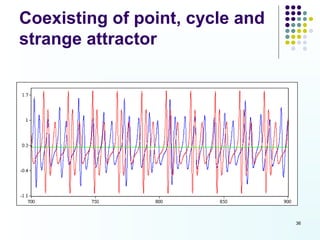
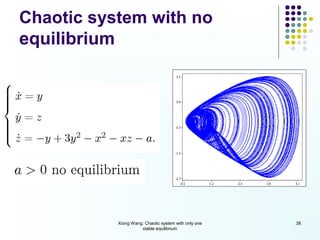
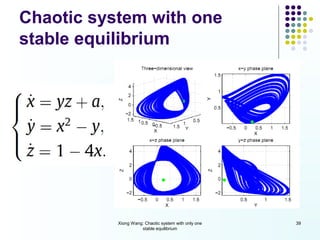
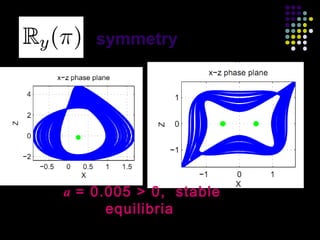
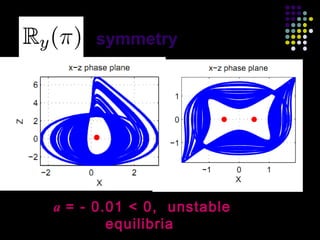
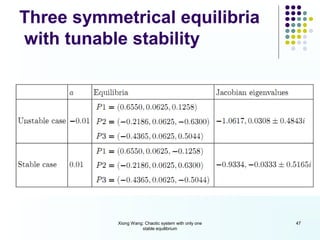
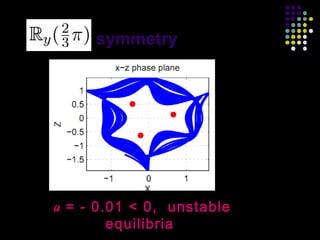
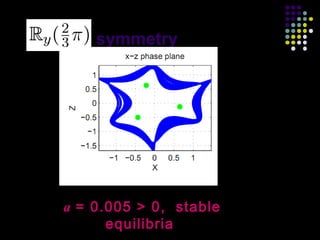
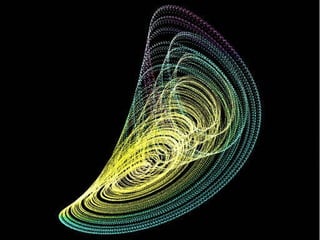
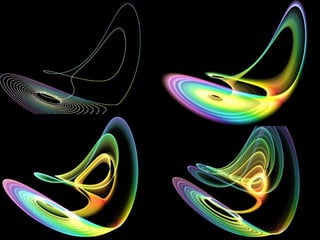
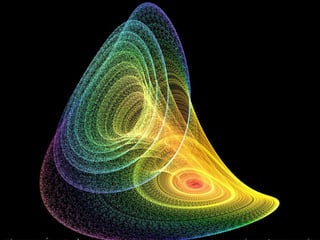
This document discusses discoveries and challenges in chaos theory. It begins by asking basic questions about the mechanisms that generate chaos and the types of systems that can exhibit chaotic dynamics. It then discusses concepts like equilibria, Jacobian matrices, Hartman-Grobman and Shilnikov theorems as they relate to the stability of equilibria and generation of chaos. Examples of chaotic systems like Lorenz, Chen and Rossler are provided. The document finds a chaotic system with one stable equilibrium, then extends this finding to systems with no equilibria, two equilibria and tunable stability. It concludes that chaos is a global phenomenon while local stability exists near equilibria.
More Related Content
Similar to CCCN Talk on Stable Chaos
CCCN Talk on Stable Chaos
- 1. Discoveries and Challenges inChaos Theory Xiong Wang 王雄 Supervised by: Prof. Guanrong Chen Centre for Chaos and Complex Networks City University of Hong Kong
- 2. Some basic questions? What’s the fundamental mechanism in generating chaos? What kind of systems could generate chaos? Could a system with only one stable equilibrium also generate chaotic dynamics? Generally, what’s the relation between a chaotic system and the stability of its equilibria? 2
- 3. Equilibria An equilibrium(or fixed point) of an autonomous system of ordinary differential equations (ODEs) is a solution that does not change with time. The ODE x = f ( x ) has an equilibrium & solution xe , if f ( xe ) = 0 Finding such equilibria, by solving the f ( x) = 0 equation analytically, is easy only in a few special cases. 3
- 4. Jacobian Matrix The stability of typical equilibria of smooth ODEs is determined by the sign of real parts of the system Jacobian eigenvalues. Jacobian matrix: 4
- 5. Hyperbolic Equilibria The eigenvalues of J determine linear stability of the equilibria. An equilibrium is stable if all eigenvalues have negative real parts; it is unstable if at least one eigenvalue has positive real part. The equilibrium is said to be hyperbolic if all eigenvalues have non-zero real parts. 5
- 6. Hartman-Grobman Theorem Thelocal phase portrait of a hyperbolic equilibrium of a nonlinear system is equivalent to that of its linearized system. 6
- 7. Equilibrium in 3D: 3real eigenvalues 7
- 8. Equilibrium in 3D: 1real + 2 complex-conjugates 8
- 9.
- 10.
- 11. Illustration of typicalhomoclinic and heteroclinic orbits 11
- 12. Review of thetwo theorems Hartman-Grobman theorem says nonlinear system is the ‘same’ as its linearized model Shilnikov theorem says if saddle-focus + Shilnikov inequalities + homoclinic or heteroclinic orbit, then chaos exists Most classical 3D chaotic systems belong to this type Most chaotic systems have unstable equilibria 12
- 13. Equilibria and eigenvaluesof several typical systems 13
- 14. Lorenz System x = a( y − x) & y = cx − xz − y & z = xy − bz , & a = 10, b = 8 / 3, c = 28 E. N. Lorenz, “Deterministic non-periodic flow,” J. Atmos. Sci., 20, 130-141, 1963. 14
- 15. Untable saddle-focus is importantfor generating chaos 15
- 16. Chen System x = a ( y − x) & y = (c − a ) x − xz + cy & z = xy − bz , & a = 35; b = 3; c = 28 G. Chen and T. Ueta, “Yet another chaotic attractor,” Int J. of Bifurcation and Chaos, 9(7), 1465-1466, 1999. T. Ueta and G. Chen, “Bifurcation analysis of Chen’s equation,” Int J. of Bifurcation and Chaos, 10(8), 1917-1931, 2000. T. S. Zhou, G. Chen and Y. Tang, “Chen's attractor exists,” Int. J. of Bifurcation and Chaos, 14, 3167-3178, 2004. 16
- 17.
- 18.
- 19. Do these twotheorems prevent “stable” chaos? Hartman-Grobman theorem says nonlinear system is the same as its linearized model. But it holds only locally …not necessarily the same globally. Shilnikov theorem says if saddle-focus + Shilnikov inequalities + homoclinic or heteroclinic orbit, then chaos exists. But it is only a sufficient condition, not a necessary one. 19
- 20. Don’t be scarredby theorems So, actually the theorems do not rule out the possibility of finding chaos in a system with a stable equilibrum. Just to grasp the loophole of the theorems … 20
- 21. Try to finda chaotic system with a stable Equilibrium Some criterions for the new system: 1. Simple algebraic equations 2. One stable equilibrium To start with, let us first review some of the simple Sprott chaotic systems with only one equilibrium … 21
- 22.
- 23. Idea 1. Sprott systems I, J, L, N and R all have only one saddle-focus equilibrium, while systems D and E are both degenerate. 2. A tiny perturbation to the system may be able to change such a degenerate equilibrium to a stable one. 3. Hope it will work … 23
- 24. Finally Result Whena = 0, it is the Sprott E system When a > 0, however, the stability of the single equilibrium is fundamentally different The single equilibrium becomes stable 24
- 25. Equilibria and eigenvaluesof the new system 25
- 26.
- 27. The new system: chaoticattractor with a = 0.006 27
- 28. Bifurcation diagram a period-doublingroute to chaos 28
- 29. Phase portraits andfrequency spectra a = 0.006 a= 0.02 29
- 30. Phase portraits andfrequency spectra a= a= 0.03 0.05 30
- 31. Attracting basins ofthe equilibra 31
- 32. Conclusions We have reported the finding of a simple 3D autonomous chaotic system which, very surprisingly, has only one stable node- focus equilibrium. It has been verified to be chaotic in the sense of having a positive largest Lyapunov exponent, a fractional dimension, a continuous frequency spectrum, and a period-doubling route to chaos. 32
- 33. Theoretical challenges To befurther considered: Shilnikov homoclinic criterion? not applicable for this case Rigorous proof of the existence? Horseshoe? Coexistence of point attractor and strange attractor? Inflation of attracting basin of the equilibrium? 33
- 34. Coexisting of point,cycle and strange attractor 34
- 35. Coexisting of point,cycle and strange attractor 35
- 36. Coexisting of point,cycle and strange attractor 36
- 37. one question answered, morequestions come … Chaotic system with one stable equilibrium Chaotic system with: No equilibrium? Two stable equilibria? Three stable equilibria? Any number of equilibria? Tunable stability of equilibria? Xiong Wang: Chaotic system with only one 37 stable equilibrium
- 38. Chaotic system withno equilibrium Xiong Wang: Chaotic system with only one 38 stable equilibrium
- 39. Chaotic system withone stable equilibrium Xiong Wang: Chaotic system with only one 39 stable equilibrium
- 40. Idea Really hardto find a chaotic system with a given number of equilibria in the sea of all possibility ODE systems … Try another way… To add symmetry to this one stable system. We can adjust the stability of the equilibria very easily by adjusting one parameter Xiong Wang: Chaotic system with only one 40 stable equilibrium
- 41. The idea ofsymmetry W =Z n W plane Z plane W = (u,v) = Z = (x,y) = x+yi u+vi Symmetrical Original system system Xiong Wang: Chaotic system with only one 41 stable equilibrium (x,y,z)
- 42. symmetry XiongWang: Chaotic system with only one 42 stable equilibrium
- 43. Stability of thetwo equilibria There are two symmetrical equilibria which are independent of the parameter a The eigenvalue of Jacobian So, a > 0 stable; a < 0 unstable Xiong Wang: Chaotic system with only one 43 stable equilibrium
- 44. symmetry a = 0.005> 0, stable equilibria Xiong Wang: Chaotic system with only one 44 stable equilibrium
- 45. symmetry a = -0.01 < 0, unstable equilibria Xiong Wang: Chaotic system with only one stable equilibrium 45
- 46. symmetry XiongWang: Chaotic system with only one 46 stable equilibrium
- 47. Three symmetrical equilibria withtunable stability Xiong Wang: Chaotic system with only one 47 stable equilibrium
- 48. symmetry a = -0.01 < 0, unstable equilibria Xiong Wang: Chaotic system with only one stable equilibrium 48
- 49. symmetry a = 0.005> 0, stable equilibria Xiong Wang: Chaotic system with only one stable equilibrium 49
- 50. Theoretically we cancreate any number of equilibria … Xiong Wang: Chaotic system with only one 50 stable equilibrium
- 51. Conclusions Chaotic systemwith: No equilibrium - found Two stable equilibria - found Three stable equilibria - found Theoretically, we can create any number of equilibria … We can control the stability of equilibria by adjusting one parameter Xiong Wang: Chaotic system with only one 51 stable equilibrium
- 52. Chaos is aglobal phenomenon A system can be locally stable near the equilibrium, but globally chaotic far from the equilibrium. This interesting phenomenon is worth further studying, both theoretically and experimentally, to further reveal the intrinsic relation between the local stability of an equilibrium and the global complex dynamical behaviors of a chaotic system 52
- 53. Xiong Wang 王雄 Centrefor Chaos and Complex Networks City University of Hong Kong Email: wangxiong8686@gmail.com 53
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.