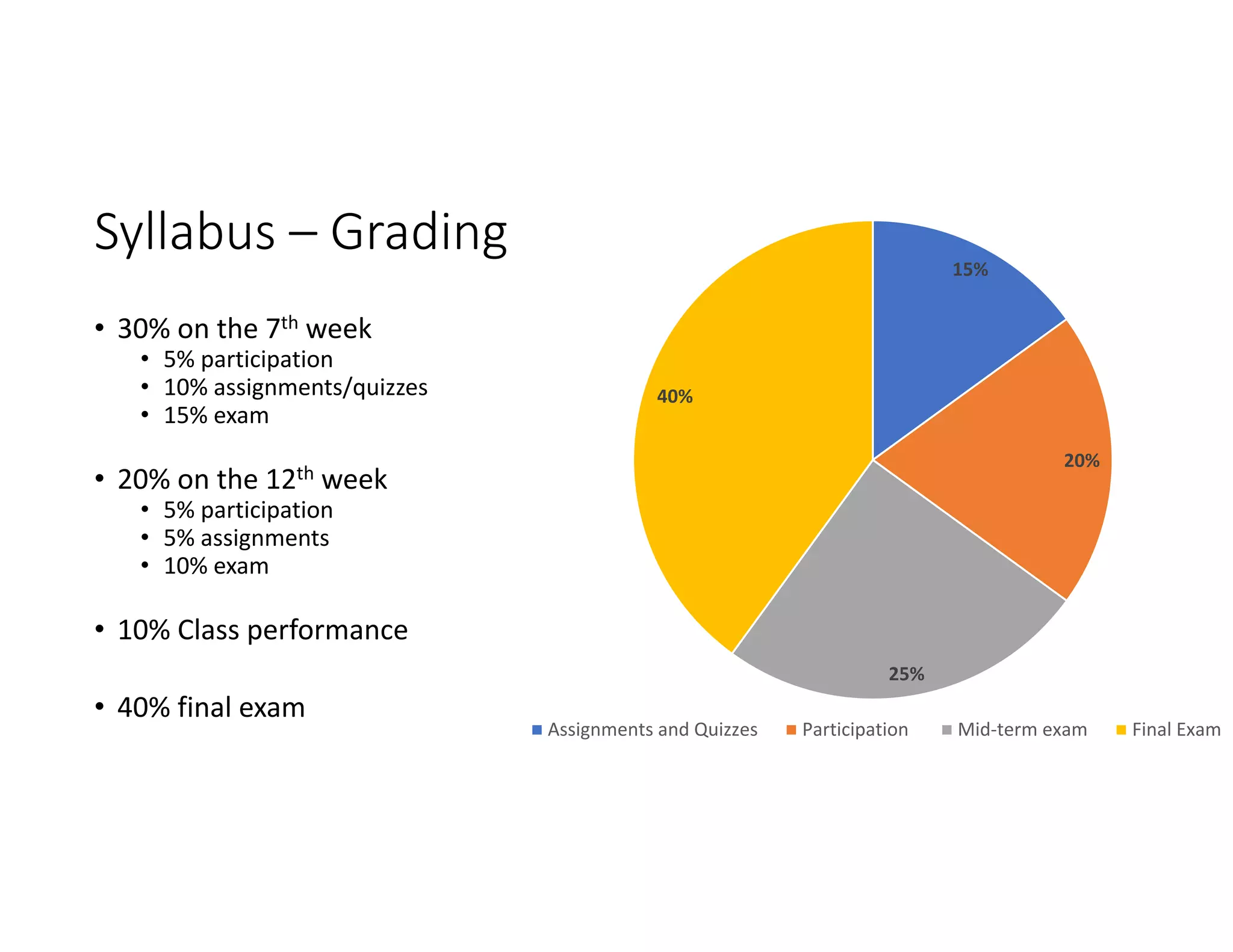
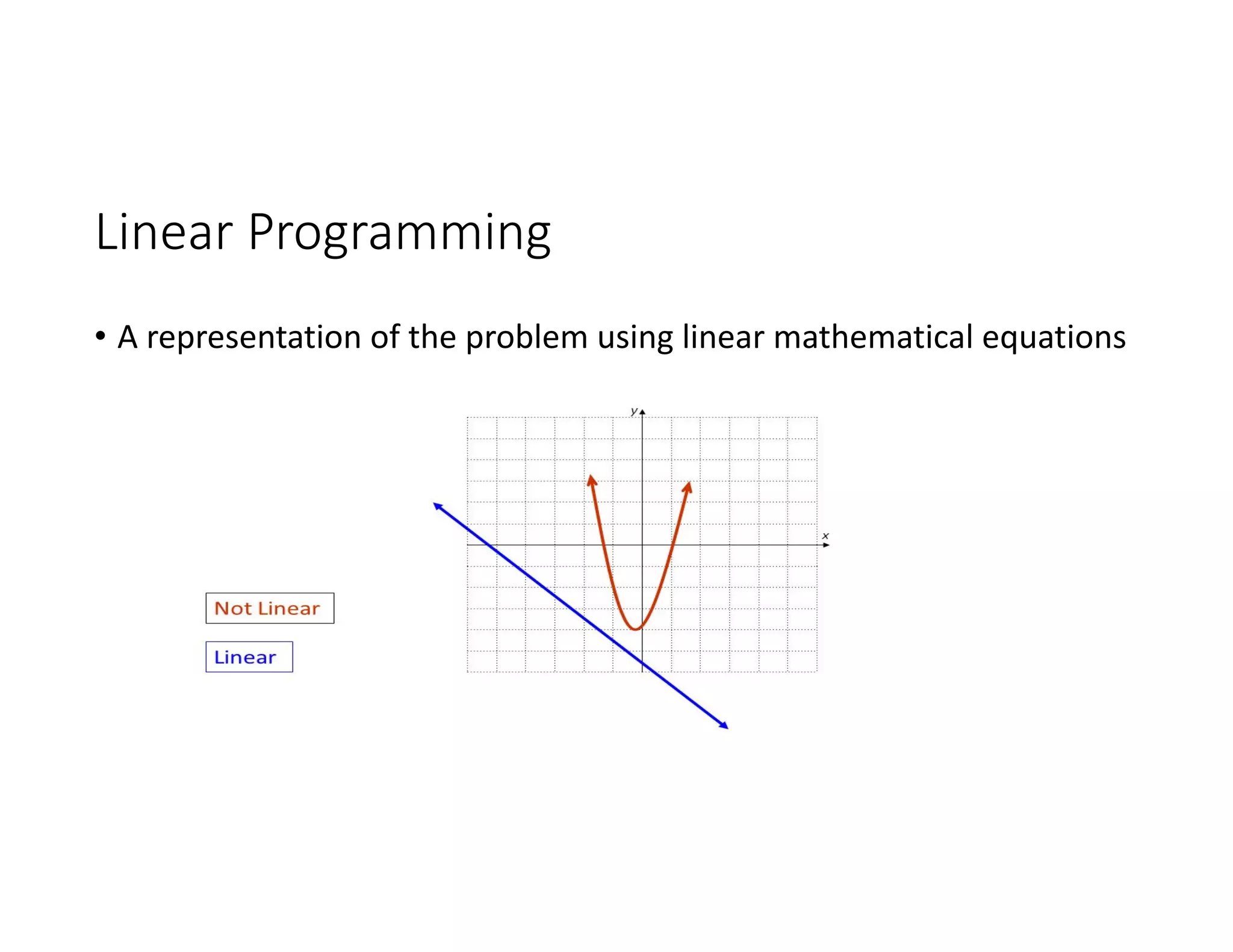
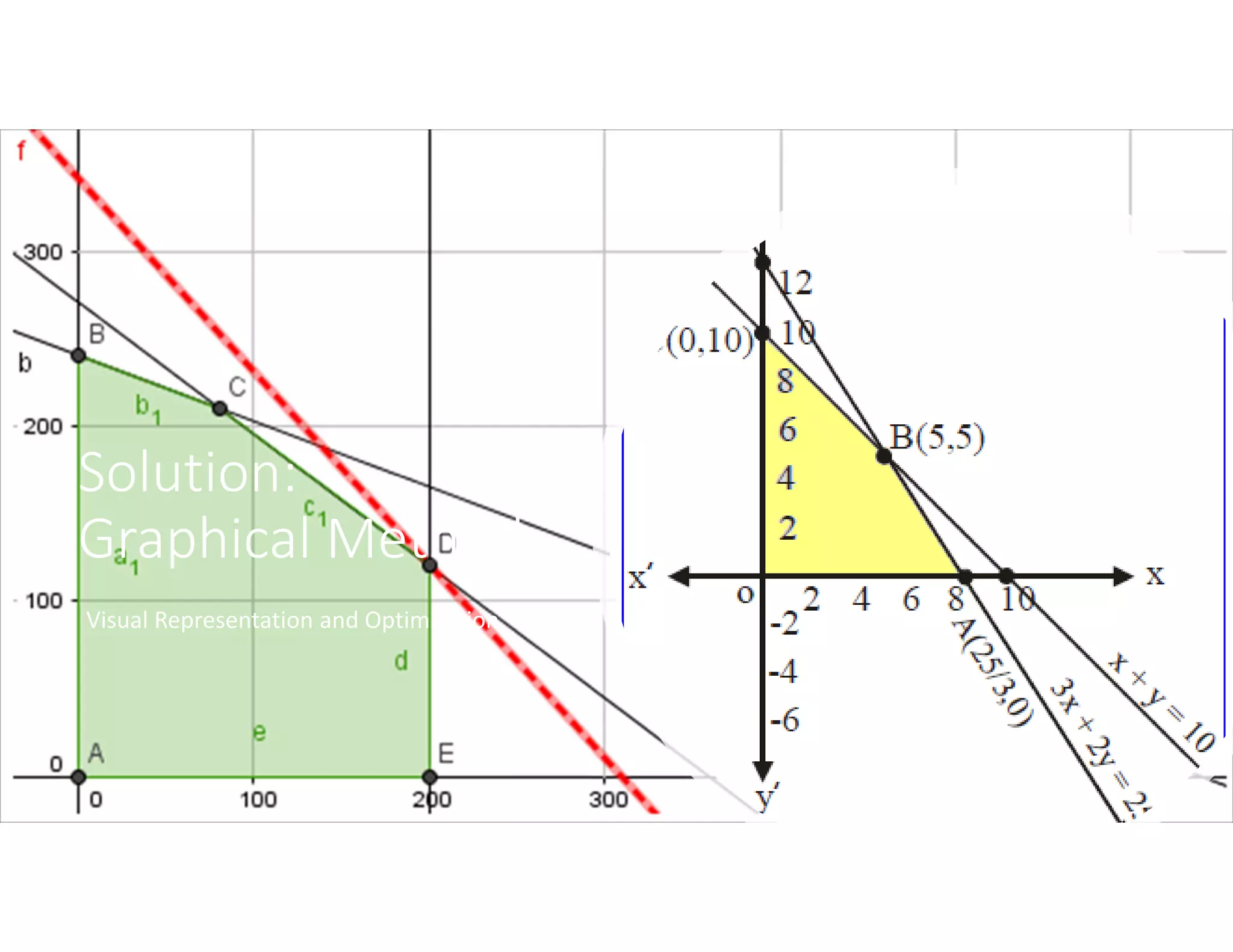
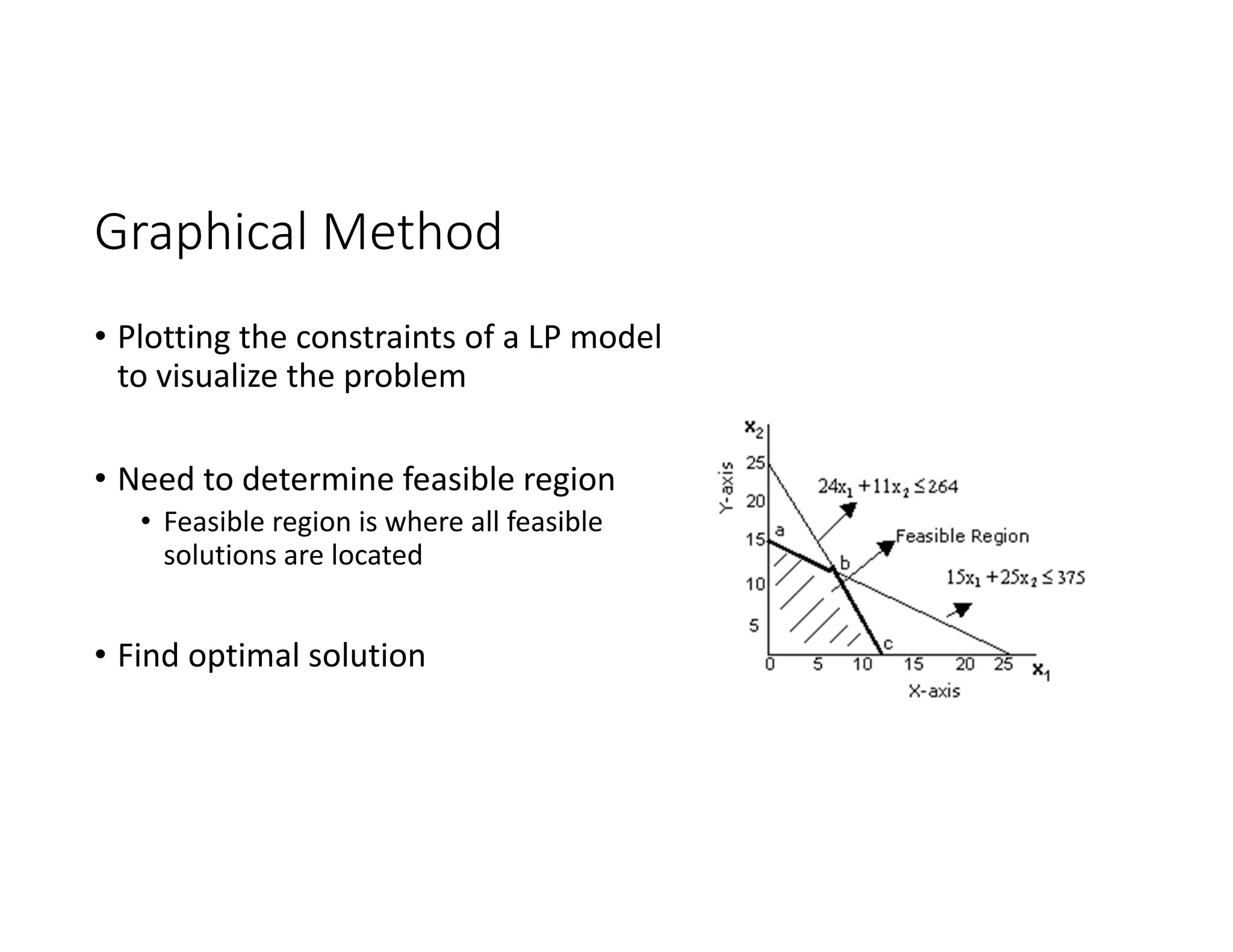
1. Define the decision variables (xA, xB), objective (minimize cost), and constraints (meeting daily nutrient requirements)
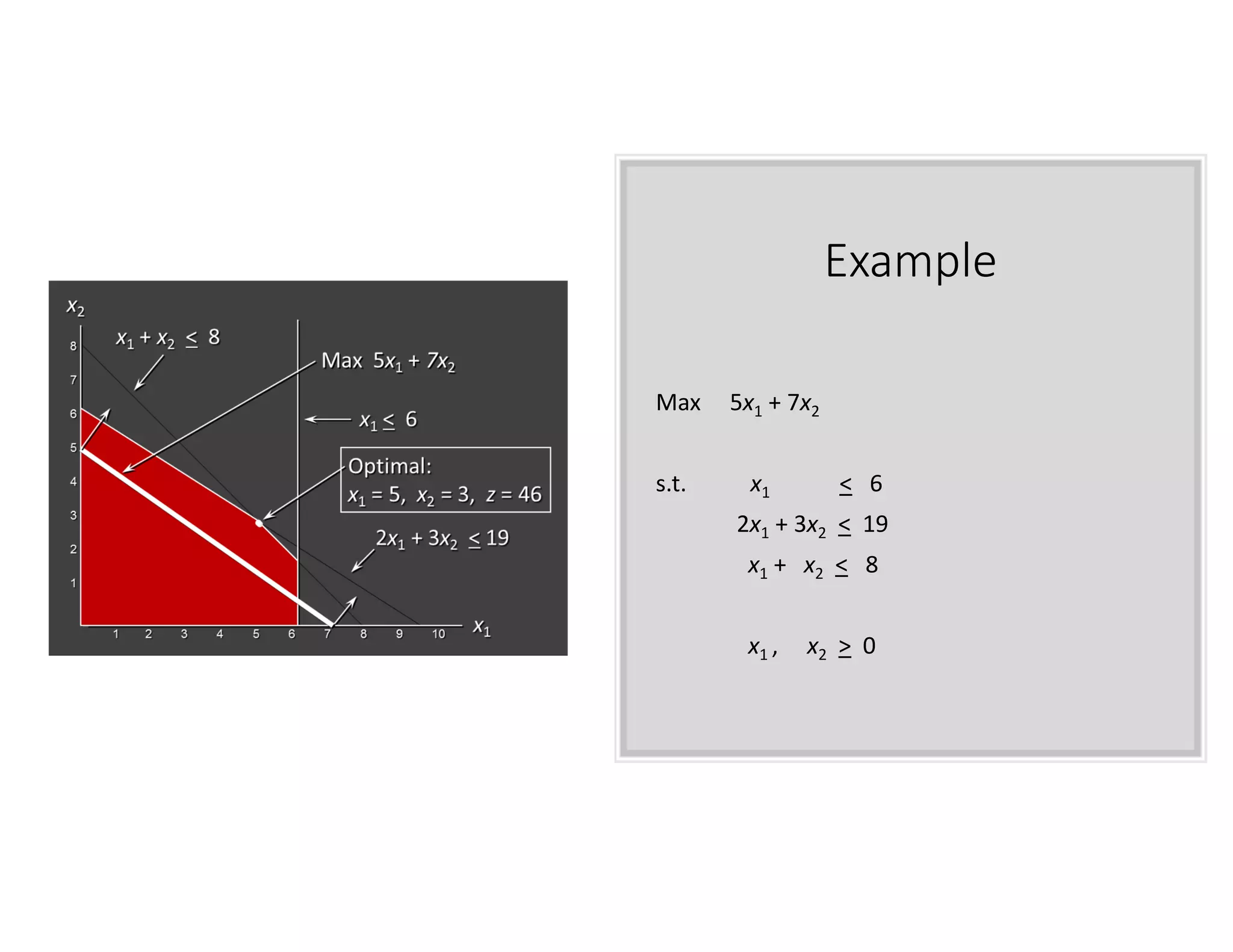
2. Write the linear program: Minimize 10xA + 12xB subject to 40xA + 30xB ≥ 150, etc.
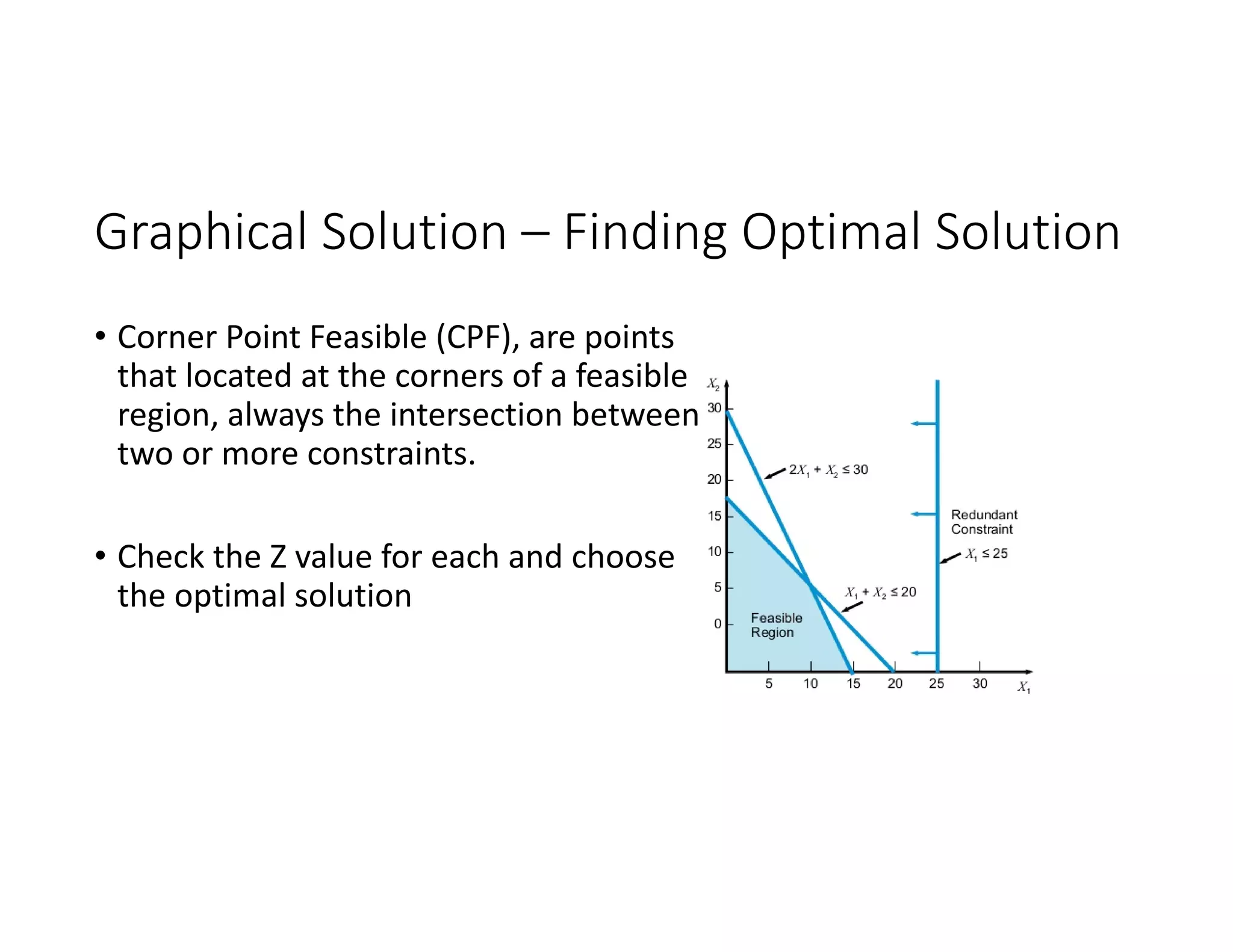
3. Graphically represent the constraints to find the feasible region
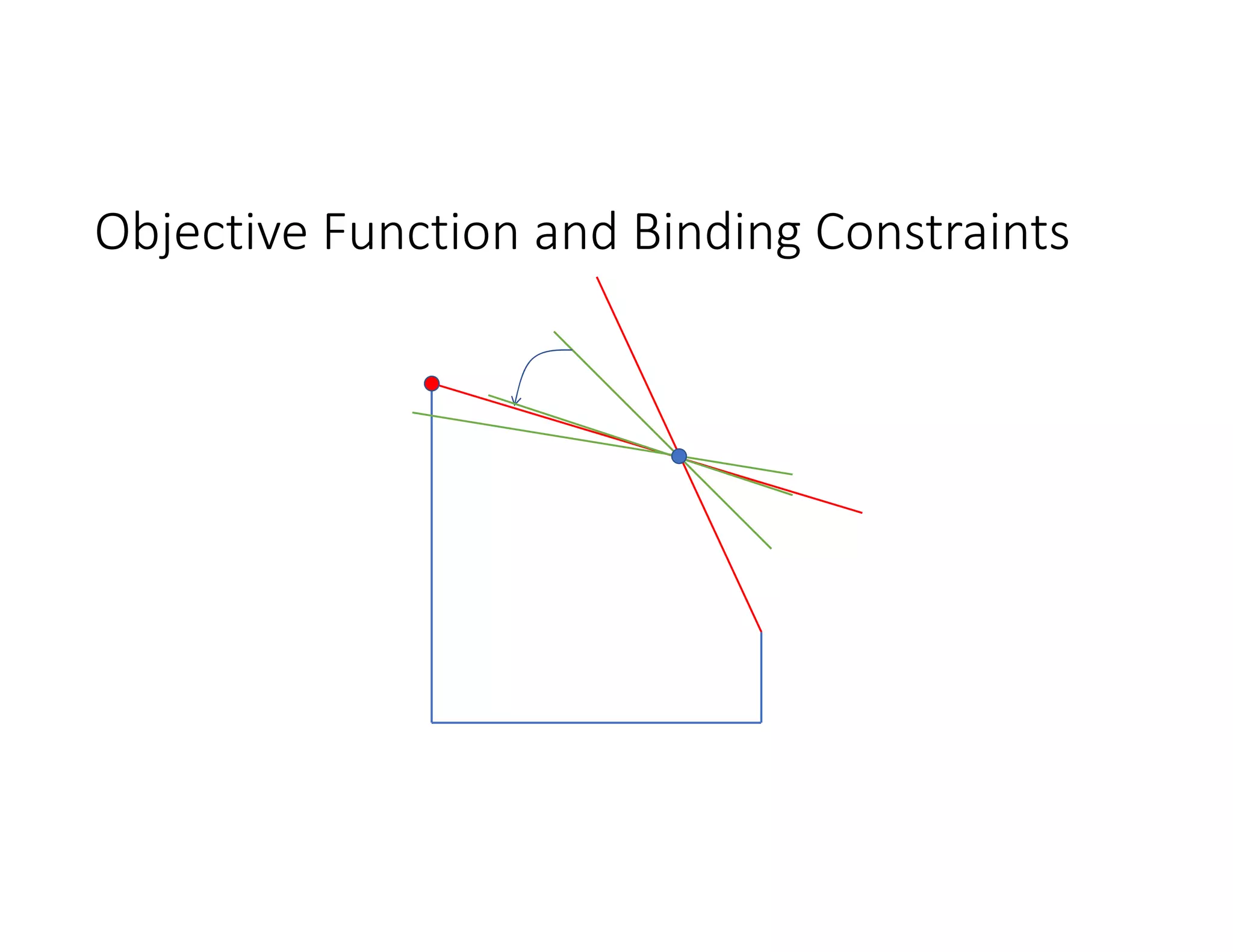
4. Identify the corner point solutions and check the objective value to find the optimal solution
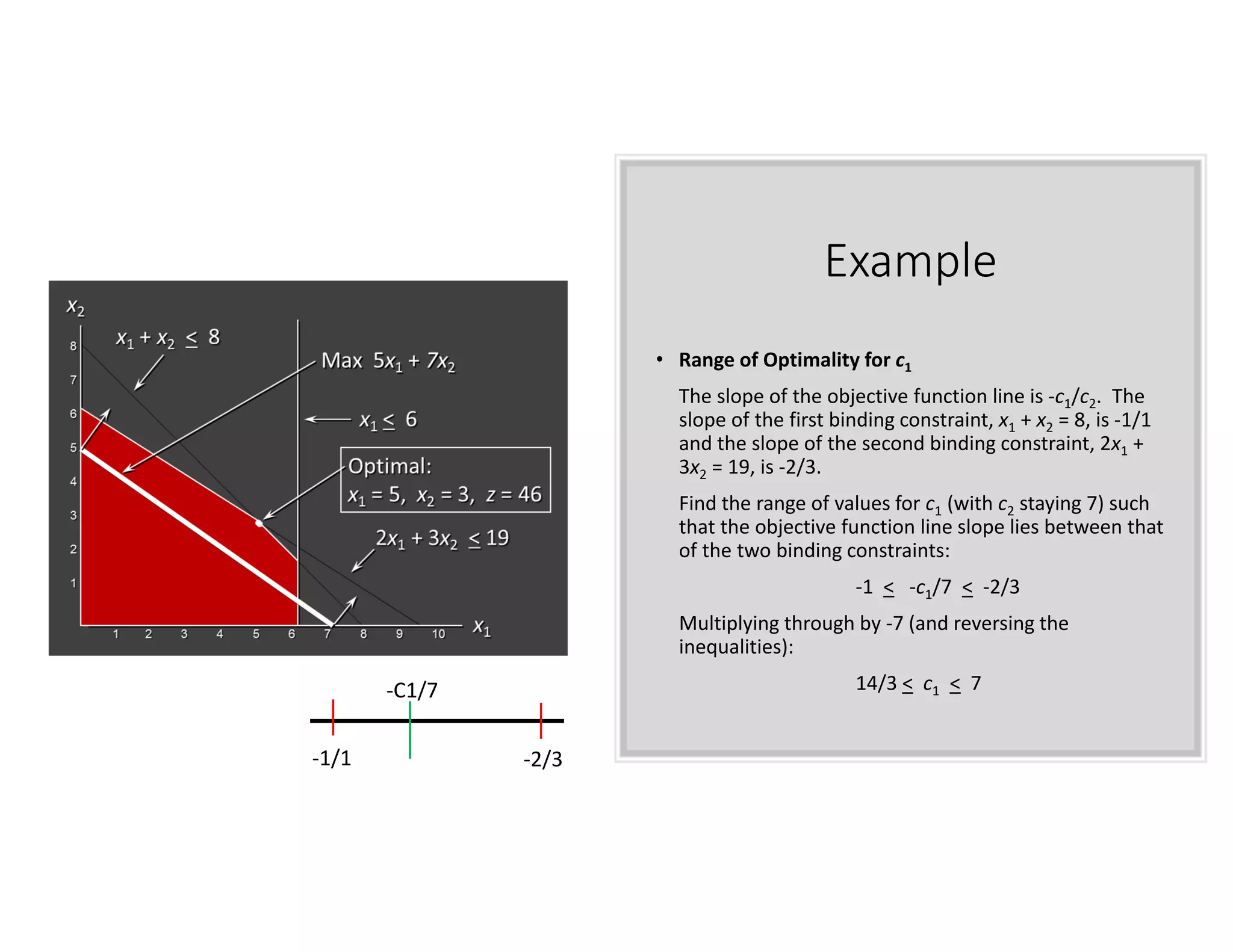
5. Conduct sensitivity analysis to determine how changes in costs would impact the optimal solution