Download as PDF, PPTX
Uploaded byCaptum Capital Limited
Captum Palisades UC 2011
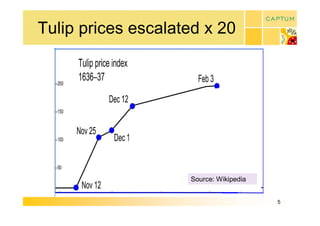
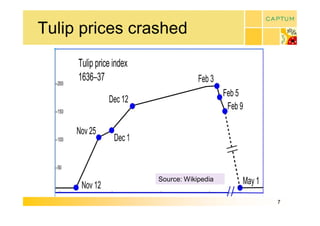
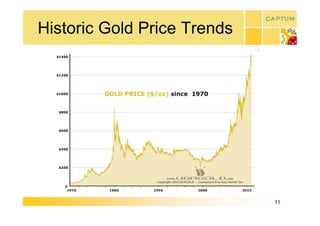
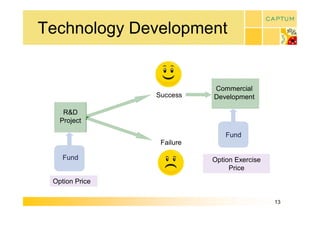
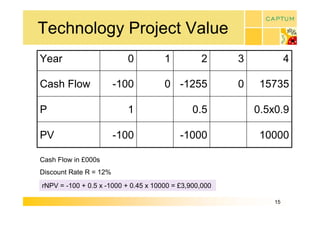
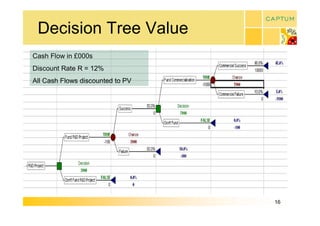
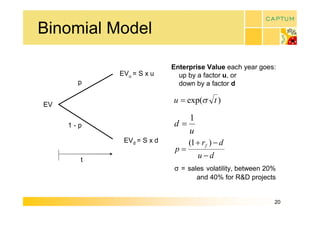
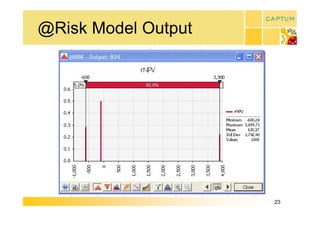
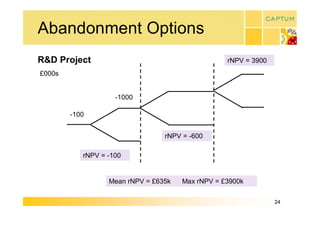
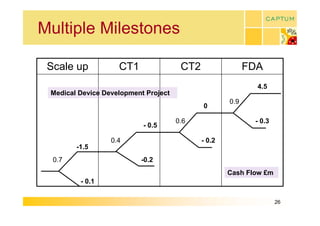
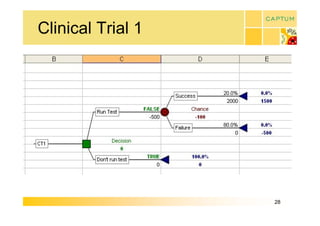
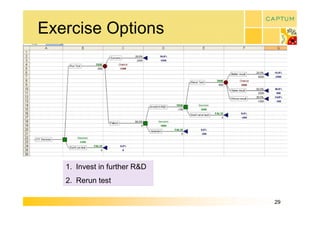
This document discusses real option valuation techniques for technology projects. It begins by providing examples of real options like options to abandon or expand a project. It then covers various valuation models like decision trees, binomial models, and Monte Carlo simulations. These models can value flexibility and account for uncertainty. The document concludes by discussing Captum Capital which provides valuation and consulting services, including upcoming events on their valuation masterclass and workshop on technology evaluation.
Captum Palisades UC 2011
- 1. Michael Brand Real Option Valuation of Technology Application of Precision Tree Palisade Risk Conference 2011 © 2011Captum Capital Limited
- 2. Valuation of Real Options § What are Real Options? § How are they valued? § Precision Tree models 2
- 3. Amsterdam – in year 1637 Bubble Tulips by Nancy Ethiel 3
- 4. The Viceroy Tulip Source: Wikipedia 4
- 5. Tulip prices escalated x 20 Source: Wikipedia 5
- 6. Future Value of a Tulip Bulb § In February 1637, a Viceroy Tulip bulb was worth 3,000fl. § You are offered an option to acquire 1000 bulbs in six months time at 3,000fl per bulb § What would you pay to acquire this option? Futures markets flourished in Amsterdam in 1637 6
- 7. Tulip prices crashed Source: Wikipedia 7
- 8.
- 9. Gold Mine Option § You own a gold mine § Geological survey estimates it contains 1 metric tonne of gold § What is the value of the mine? 9
- 10. Value of Gold Mine § Its value depends on the price of gold § Risk § You can start or stop mining depending on the price of gold § Flexibility in outcome This is a classic Real Option 10
- 11.
- 12. Real Options § Risk or Uncertainty in the…outcome § Nonlinearity: flexibility to react in different ways…so that a new set of outcomes is achieved Source: Michael Rees, Financial Modelling in Practice (2008) 12
- 13. Technology Development Commercial Success Development R&D Project Fund Failure Fund Option Exercise Price Option Price 13
- 14. Risk Adjusted NPV P C rNPV = å t t t ( + R 1 ) rNPV depends on 3 factors: •Probability, P •Cash Flow, C •Discount Rate, R Most commonly used method for valuing technology 14
- 15. Technology Project Value Year 0 1 2 3 4 Cash Flow 100 0 1255 0 15735 P 1 0.5 0.5x0.9 PV 100 1000 10000 Cash Flow in £000s Discount Rate R = 12% rNPV = 100 + 0.5 x 1000 + 0.45 x 10000 = £3,900,000 15
- 16.
- 17. Real Option Valuation § Key variables § Underlying Asset Value – Enterprise Value § Exercise Price § Term to Exercise § Volatility of Underlying Asset § Discount Rate 17
- 18. RO Valuation Methods § Black Scholes OptionPricing Model* § Binomial Model* § Monte Carlo Simulation § Decision Tree * Developed for financial option valuation 18
- 19. Black Scholes Equation Present Value of a Call Option: - r t PV = PN ( 1 ) - EXe f N ( 2 ) d d where: 2 N(d) = normal probability function log( P / EX ) + r t + s t / 2 f d = 1 EX = exercise price s t t = time to exercise log( P / EX ) + r t - s 2 t / 2 t d 2 = P = price of security s t _ ( P - P 2 ) σ = variance on return = N - 1 r = risk free rate f 19
- 20. Binomial Model Enterprise Value each year goes: EV = S x u u up by a factor u, or p down by a factor d EV s u = exp( t ) 1 1 p d = u EV = S x d d ( + r ) - d 1 f p = t u - d σ = sales volatility, between 20% and 40% for R&D projects 20
- 21.
- 22. @Risk Model 22
- 23.
- 24. Abandonment Options R&D Project rNPV = 3900 £000s 1000 100 rNPV = 600 rNPV = 100 Mean rNPV = £635k Max rNPV = £3900k 24
- 25. Strategic Decision Options § Defer Investment § Default § Expand § Contract § Shut Down and Restart § Abandon Lenos Trigeorgis, Real Options (1996) 25
- 26. Multiple Milestones Scale up CT1 CT2 FDA 4.5 Medical Device Development Project 0.9 0 0.6 0.3 0.5 0.4 0.2 1.5 0.7 0.2 Cash Flow £m 0.1 26
- 27.
- 28.
- 29. Exercise Options 1. Invest in further R&D 2. Rerun test 29
- 30. Summary § Decision Trees are a viable approach to Real Option Valuation: § Simple to construct using Precision Tree § Flexible – changes of strategy § Transparent – ease of communication § Credible not a “Black Box” 30
- 31. About Captum… § Formed in 2004 § Transatlantic presence § Life science sector consulting: § Business development, valuation, partnering § MasterClasses: § Valuation Masterclass attended by over 500 executives in UK and Europe § Internet virtual communities § Sensor100 31
- 32. Coming Events § MasterClass: Company Valuation th London, 25 May 2011 § Workshop: Evaluating Technology LES International Conference th London, 8 June 2011 32
- 33. Captum Growth Series Valuing Technology nd 2 edition To be published May 2011 33
- 34. Contact Captum Capital Limited Cumberland House 35 Park Row Michael Brand Nottingham NG1 6EE e: mjb@captum.com United Kingdom t: +44 (0) 115 988 6154 m: +44 (0) 7980 257 241 www.captum.com 34