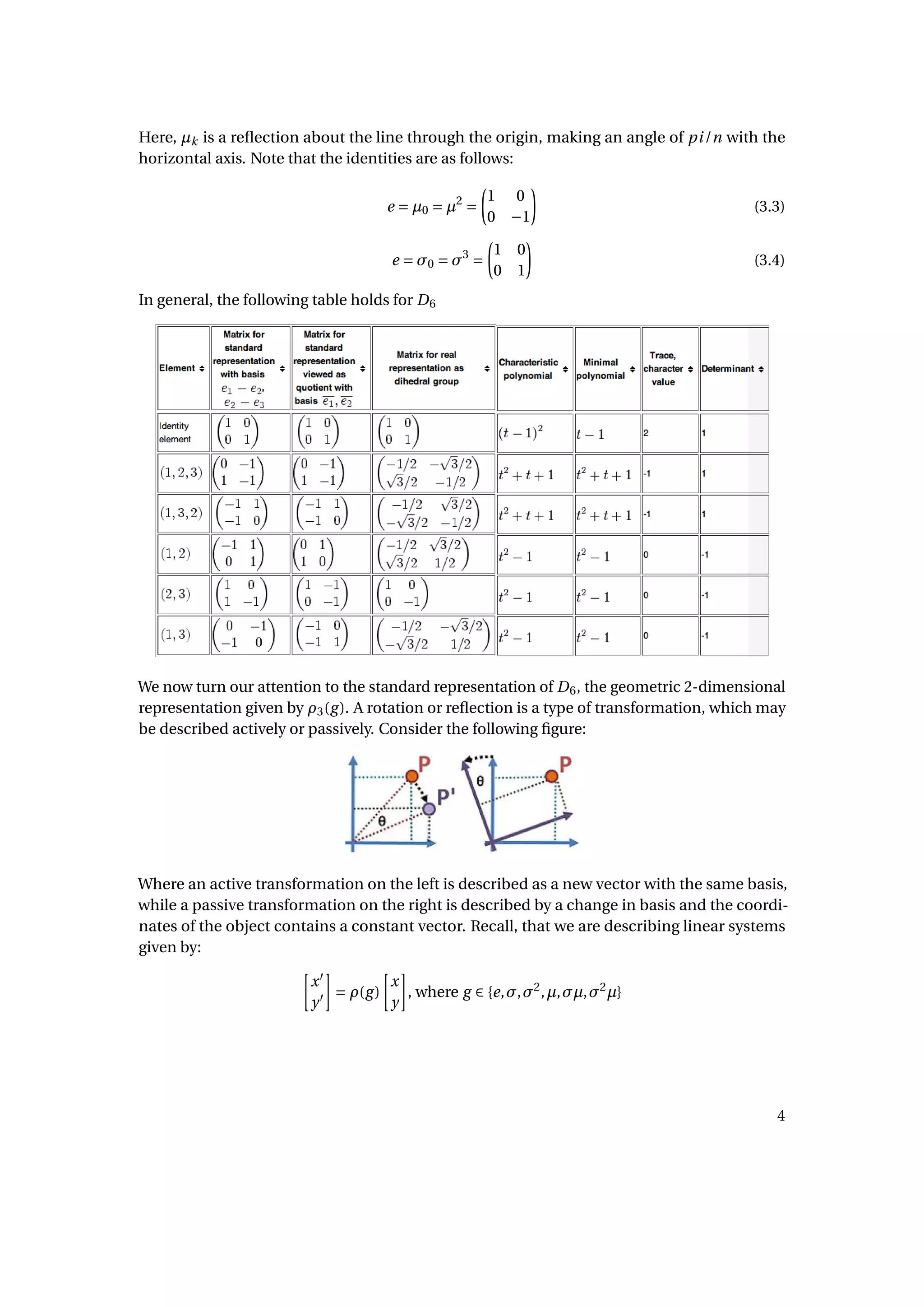
The document discusses the representation theory and symmetries of the dihedral group d6, which pertains to the symmetries of an equilateral triangle. It outlines the properties of groups and details how the group structure is preserved through homomorphisms, ultimately linking group elements to transformations in vector spaces using matrices. Various representations of d6, including trivial and geometric ones, are explored, emphasizing the relationship between group operations and their corresponding transformations.

1. STANDING WAVES: THE EQUILATERAL TRIANGLE
Group Representation Theory & Symmetry
Brian R. Covello
April 23, 2013
1 ABSTRACT ALGEBRA: GROUPS
Definition: A group G is a set of elements G = (I,a,b,c,...) and a given operation denoted ◦
between the elements of a group. A group has the following four properties:
1. Closure: Given a,b ∈ G, then a ◦b ∈ G
2. Identity: ∃ I ∈ G such that e ◦ a = a. We call this the identity element.
3. Inverse: For any element a within the group, ∃b ∈ G such that a ◦b = e, where b is called
the inverse of a and is denoted a−1
= b.
4. Associativity: a ◦b ◦c = a ◦(b ◦c) = (a ◦b)◦c
The group of interest is the non-abelian dihedral group D6, which represents the symmetries
of an equilateral triangle. A homomorphism from G to H is a function f : G → H such that
f (a ◦ b) = f (a) ◦ f (b). Thus, the group structure is preserved. Additionally, GLn(R) is the
general linear group where:
GLn ={invertible n x n matrices with entries in the Real numbers}
.
Thus, a homomorphism ρ : G → GLn(R) takes the group described by D6 and maps each group
element to a transformation of the vector space consistent with the multiplication table of
the group. Yet what exactly is a multiplication table? And can we best understand D6 and
symmetry of the equilateral triangle?
1

2. Figure 2.1: Symmetries of an Equilateral Triangle
2 SYMMETRY OF AN EQUILATERAL TRIANGLE
If we choose to label the vertices of a triangle 1,2,3 respectively, then we may describe these
vertex points by the symmetric group S3 given by the permutations of the set (1,2,3). Theere are
two ways in which we may transform the triangle. Either a rotation, of 2πk
n counter clockwise
denoted by σ, or a reflection across denoted by µ. Note above, that there are several types of
reflections that may be involved. We may then correlate changes to S3 to arrangments of the
set (1,2,3) as movement of the numbers representing vertices. In general, D6 is isomorphic to
S3, which contains all the permutations. From the figure above
a = (2,3) b = (1,3) c = (1,2) σ = (1,3,2) σ2
= (1,2,3) (2.1)
Thus, the multiplication table may be given by:
Observe that µσµ = σ−1
. Since µ = µ−1
, µσµ = σ−1
can be rewritten as µσ = σ−1
µ or as
µσ−1
= σµ. Thus, one can always move µ past σ at the expense of replacing σ with σ−
. For
example:
(σ2
µ)(σµ) = σ2
(σ−1
µ)µ = σ (2.2)
Taking this into consideration with the fact that σ3
= e, it becomes clear the product of
the set {e,σ,σ2
,µ,σµ,σ2
µ} will always be another element of the same set. Furthermore, if
2

3. σi
µj
= σk
µl
then σi−k
= µl−j
, with the permutation which is both a power of σ and µ being
the identity. It follows that σi
= σk
and µj
= µl
. The six expressions σi
µj
i ∈ (0,1,2), j ∈ (0,1)
corresponds to six distinct elements of the group. Thus, the set {e,σ,σ2
,µ,σµ,σ2
µ} describes
the entire dihedral group D6 with generators σ and µ.
We find that there are three trivial representations of D6.
1. The trivial 1 dimensional representation given by e. This may be described by ρ1(g) = 1
for every g ∈ D6
2. The sign representation maps even permutations in D6 such as {e, (1,2,3), (1,3,2)} to
+1 and odd mutations in D6 such as {(1,2), (1,3), (2,3)} to -1. In this manner, this repre-
sentation determines whether or not a reflection given by µ has occurred. This may be
described by ρ2(σ) = 1 or ρ2(µ) = −1.
3. The geometric 2-dimensional representation given by ρ3(g). It is well known that
non-abelian groups (groups that are not commutative) have at least one irreducible
representation above order 1. This representation will be discussed in detail in section 3.
Generalizing these observations for a regular n-sided polygon of the dihedral group D2n,
we find there are n rotation symmetries through angles of 2kπ/n where k ∈ {1,2,...,n −1} and
there are n reflection symmetries in the n lines which are the bisectors of the internal angle
and the perpendicular bisectors of the sides. If n is odd, then the bisector of an angle at a
vertex coincides with the bisector of the angle at the opposite side. We let σ be clockwise
rotation through 2π/n and µ any of the reflections, then σn
= µ2
= e and µσµ = σ−1
. There
are 2n elements of the group given by e,σ,σ2
,...,σn−1
,µ,σµ,σ2
µ,...,σn−1
µ. Additionally, the
multiplication table is determined by these relations.
3 HOMOMORPHISM ρ : G → GLn(R) AND TRANSFORMATIONS
A homomorphism from G to H is a function f : G → H such that f (a ◦b) = f (a)◦ f (b). Thus,
the group structure is preserved. Additionally, GLn(R) is the group of invertible linear transfor-
mations on the vector space V where:
GLn ={invertible n x n matrices with entries in the Real numbers}
.
Thus, a homomorphism ρ : G → GLn(R) takes the group described by D6 and maps each group
element to a transformation of the vector space consistent with the multiplication table of the
group in section 2.
The rotations around the origin given by σ and the reflection µ is represented by matrices
in the following manner:
σk =
cos(2πk/n) −sin(2πk/n)
sin(2πk/n) cos(2πk/n)
(3.1)
µk =
cos(2πk/n) sin(2πk/n)
sin(2πk/n) −cos(2πk/n)
(3.2)
3

4. Here, µk is a reflection about the line through the origin, making an angle of pi/n with the
horizontal axis. Note that the identities are as follows:
e = µ0 = µ2
=
1 0
0 −1
(3.3)
e = σ0 = σ3
=
1 0
0 1
(3.4)
In general, the following table holds for D6
We now turn our attention to the standard representation of D6, the geometric 2-dimensional
representation given by ρ3(g). A rotation or reflection is a type of transformation, which may
be described actively or passively. Consider the following figure:
Where an active transformation on the left is described as a new vector with the same basis,
while a passive transformation on the right is described by a change in basis and the coordi-
nates of the object contains a constant vector. Recall, that we are describing linear systems
given by:
x
y
= ρ(g)
x
y
, where g ∈ {e,σ,σ2
,µ,σµ,σ2
µ}
4

5. In linear algebra, a basis is a set of linearly independent vectors that in a multitude of linear
combinations can represent every vector in a given vector space. Thus in a vector space R2
, we
denote {e1,e2} as a basis and consider the vector v =
x
y
= xe1 + ye2. In active transformation,
v = ρ(g)v. A passive transformation must transform according to the inverse of the active
transformation operator ρ(g). A passive transformation is what allows consistent vectors, as
such, the following action is well defined with f (x, y) representing the Helmholtz Equation:
(g · f )(x, y) = f (ρ3(g)−1 x
y
) (3.5)
These characteristics allow ρ : G → GLn(R) to be a well defined homomorphism.
1. For GL(R) to accurately represent the situation, only invertible matrices can be used
because we must be able to rotate in both directions, obtaining similar solutions at some
point.
2. If we input f (x, y) = 0 then the right hand side of the equation would have determi-
nant=0 and ρ(g) would not be invertible. If ρ(g) is not invertible then the relationship
defining the dihedral group D2n (µ(σ)) = (σ−1
)µ would be lost. This would destroy group
structure.
3. On the right hand side ρ−1
(g) is really specifying a change of basis - if ρ(g) represents a
rotation then ρ−1
(g) could represent a clockwise rotation of the basis which is equivalent
to a counterclockwise rotation of the vectors. Another way to describe this situation is
(g · f )(x, y) would imply that this equals g · f (x, y) = f (ρ−1
(g)(x, y))
Yet these conclusions are inefficient to explain the necessity of the inverse matrix within this
equation. Our examination is one in which a representation is constructed within a function
space. In general, we consider a a map associating to every vector −→r a transformed vector
−→r = T −→r . Where T represents the group of rotations and reflections as previously mentioned.
Any scalar function denoted f at −→r will have a different value given by ft . Where f (−→r ) and
(ft (−→r )) are related by:
ft (−→r ) = f (T −1−→r ) (3.6)
. We define ft (−→r ) = Ot f (−→r ) to obtain:
Ot f (−→r ) = f (T −1−→r ) (3.7)
If the elements T form a group, then OSOR = OSR. As alluded to, the operator OR is applied first
and the operator OS acts on the whole expression placed right to it, forming a representation
of the group within a function space. More clearly,
OSOR f (−→r ) = OS f (R−1−→r ) = f (R−1
S−1−→r ) = f ((SR)−1−→r ) = OSR f (−→r ) (3.8)
5