Data Analytics

1. Bivariate Statistics
Notes and Solved Examples

2. Concept of Bivariate Statistics
• Bivariate statistics analyzes the relationship
between two quantitative variables.
• - Do two variables move together?
• - Is the relationship positive or negative?
• - Is it strong or weak?
• Key tools:
• - Covariance
• - Correlation (Pearson and Spearman)

3. Covariance
• Formula:
• Cov(X, Y) = (1 / (n - 1)) * Sum[(x_k - )(y_k - ȳ)]
x̄
• Interpretation:
• - Positive: both increase together
• - Negative: one increases, other decreases
• - Zero: no linear relationship

4. Covariance - Solved Example
• X = [60, 70, 80, 90, 100], Y = [160, 165, 170,
175, 180]
• Mean = 80, Ȳ = 170
X̄
• Sum[(x_k - )(y_k - ȳ)] = 500
x̄
• Cov(X,Y) = 500 / 4 = 125

5. Pearson Correlation Coefficient
• Formula:
• r_xy = Cov(X, Y) / (s_X * s_Y)
• Range: -1 to +1
• +1: perfect positive
• 0: no linear relation
• -1: perfect negative

6. Pearson Correlation - Solved
Example
• s_X = s_Y = sqrt(250) ≈ 15.81
• r_xy = 125 / (15.81 * 15.81) ≈ 0.5
• Moderate positive linear relationship

7. Spearman Rank Correlation
• Formula:
• r_s = 1 - [6 * Sum(d_i^2)] / [n(n^2 - 1)]
• Ranks:
• X = [1, 2, 3, 4, 5], Y = [2, 1, 3, 5, 4]
• d_i = [-1, 1, 0, -1, 1], Sum = 4
• r_s = 1 - (6 * 4) / (5 * 24) = 0.8

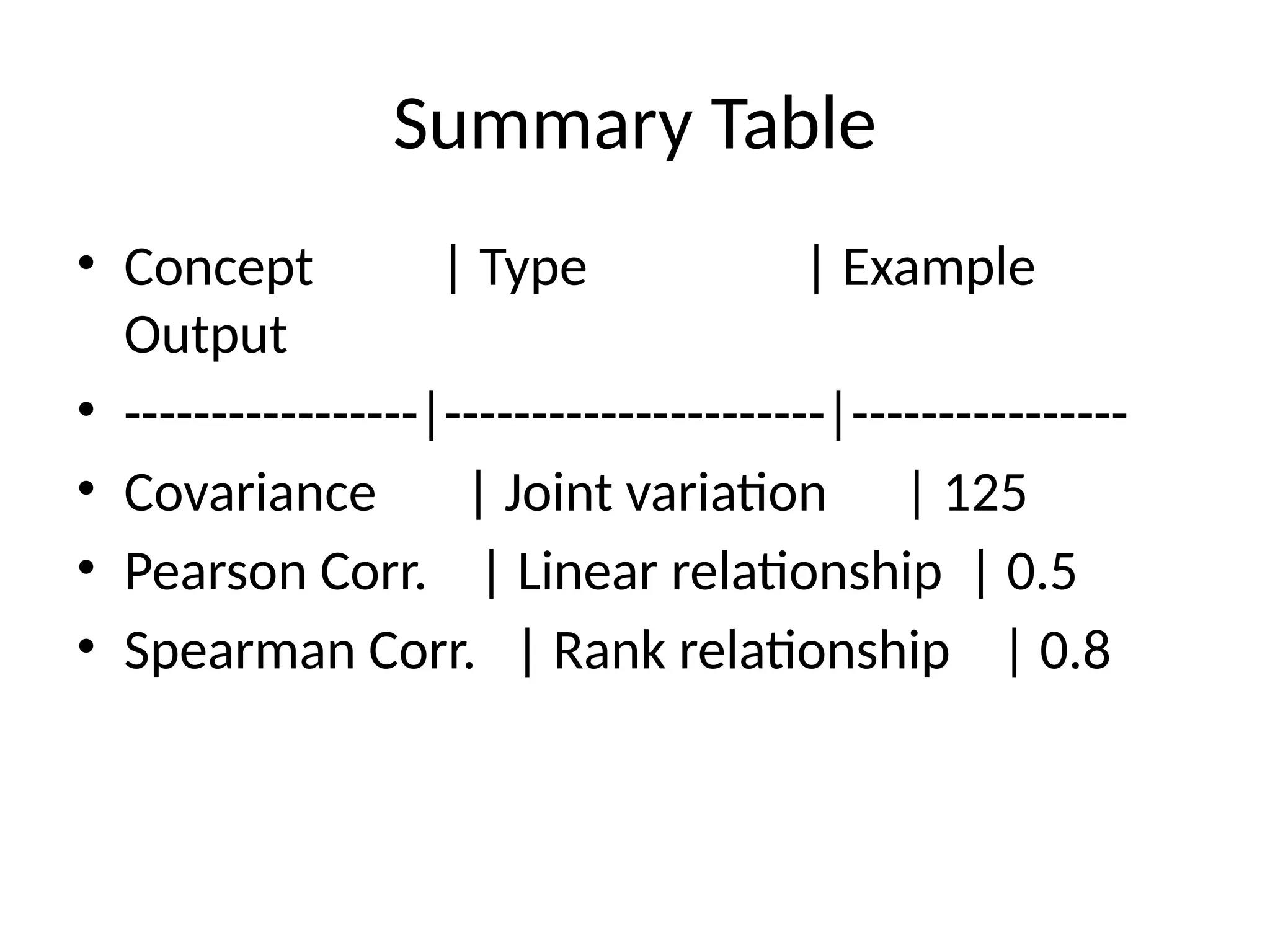
8. Summary Table
• Concept | Type | Example
Output
• -----------------|----------------------|----------------
• Covariance | Joint variation | 125
• Pearson Corr. | Linear relationship | 0.5
• Spearman Corr. | Rank relationship | 0.8