Tài liệu trình bày nội dung bài giảng toán cao cấp cho sinh viên tin học kinh tế, bao gồm các chủ đề như ma trận, định thức, và hệ phương trình tuyến tính. Chương 1 tập trung vào ma trận và các phép toán liên quan, trong khi chương 2 đề cập đến hàm số một biến và các khái niệm liên quan đến giới hạn và tính liên tục. Các mô hình toán học cũng được giới thiệu để áp dụng trong phân tích kinh tế.




![Chương 1
Ma trận, định thức, hệ phương trình tuyến
tính
Trong chương trình bày các khái niệm cơ bản về ma trận; định thức của ma trận
vuông, ma trận nghịch đảo của ma trận vuông, hạng của ma trận. Các khái niệm cơ bản
về hệ phương trình tuyến tính; hệ Crame, hệ phương trình tuyến tính thuần nhất cũng
như cách giải các hệ phương trình này. Giới thiệu một số mô hình tuyến tính trong phân
tích kinh tế.
1.1. Ma trận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2. Định thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3. Ma trận nghịch đảo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.4. Hạng của ma trận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.5. Hệ phương trình tuyến tính tổng quát . . . . . . . . . . . . . . . . . . . . . . . . 12
1.6. Một số mô hình tuyến tính trong phân tích kinh tế . . . . . . . . . . . 19
1.7. BÀI TẬP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.1. Ma trận
1.1.1. Định nghĩa
Định nghĩa 1.1.1. Cho m, n là hai số nguyên dương. Ma trận cấp m × n là một bảng
m × n số hình chữ nhật gồm m hàng, n cột có dạng
A =
a11 a12 · · · a1n
a21 a22 · · · a2n
...
...
...
...
am1 am2 · · · amn
=
a11 a12 · · · a1n
a21 a22 · · · a2n
...
...
...
...
am1 am2 · · · amn
hoặc viết tắt A = [aij]m×n,
(1.1.1)
trong đó aij, i = 1, 2, . . . , m, j = 1, 2, . . . , m, là phần tử ở hàng thứ i và cột thứ j của ma
trận A.
• Ma trận hàng: Là ma trận chỉ có một hàng và n cột, ký hiệu là
A = a11 a12 . . . a1n = [a1j]1×n, j = 1, 2, . . . , n.](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-5-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
• Ma trận cột: Là ma trận có m hàng và chỉ có một cột, ký hiệu là
A =
a11
a21
...
am1
= [ai1]m×1, i = 1, 2, . . . , m.
• Ma trận chuyển vị: Xét ma trận A = [aij]m×n. Đổi hàng thành cột và cột thành
hàng của ma trận A ta được ma trận mới gọi là ma trận chuyển vị của ma trận A,
ký hiệu là At
. Vậy At
= [aji]n×m.
• Ma trận vuông cấp n: Là ma trận có số hàng bằng số cột bằng n, ký hiệu là
A =
a11 a12 · · · a1n
a21 a22 · · · a2n
...
...
...
...
an1 an2 · · · ann
= [aij]n×n.
Các phần tử a11, a22, . . . , ann được gọi là các phần tử nằm trên đường chéo chính.
• Ma trận đối xứng: Là ma trận vuông có các phần tử nằm ở vị trí đối xứng bằng
nhau, tức là aij = aji, i = 1, 2, . . . , n, j = 1, 2, . . . , n.
• Ma trận chéo: Là ma trận vuông có các phần tử nằm ngoài đường chéo chính đều
bằng không, tức là aij = 0, i = j, i = 1, 2, . . . , n, j = 1, 2, . . . , n.
• Ma trận đơn vị cấp n: Là ma trận chéo mà các phần tử trên đường chéo chính đều
bằng 1, ký hiệu là In.
• Ma trận tam giác trên: Là ma trận vuông thỏa mãn aij = 0, i > j, i = 1, 2, . . . , n, j =
1, 2, . . . , n hay
A =
a11 a12 · · · a1n
0 a22 · · · a2n
...
...
...
...
0 0 · · · ann
.
• Ma trận tam giác dưới: Là ma trận vuông thỏa mãn aij = 0, i < j, i = 1, 2, . . . , n, j =
1, 2, . . . , n hay
A =
a11 0 · · · 0
a21 a22 · · · 0
...
...
...
...
an1 an2 · · · ann
.
• Ma trận không: Là ma trận mà mọi phần tử đều bằng không, ký hiệu O.
Ngô Mạnh Tưởng 2](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-6-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
• Hai ma trận được gọi là bằng nhau nếu chúng cùng cấp và các phần tử ở vị trí
tương ứng bằng nhau.
Các ví dụ:
• Ma trận A =
1 2 3
0 5 4
; ma trận chuyển vị At
=
1 0
2 5
3 4
;
• Ma trận vuông cấp 3: B =
5 −1 0
3 8 2
0 6 4
;
• Ma trận chéo: C =
1 0 0
0 4 0
0 0 −2
;
• Ma trận đối xứng: D =
1 0 5
0 3 7
5 7 2
;
• Ma trận đơn vị cấp 3: I =
1 0 0
0 1 0
0 0 1
.
1.1.2. Các phép toán trên ma trận
a. Phép cộng hai ma trận cùng cấp
Cho hai ma trận cùng cấp A = [aij]m×n; B = [bij]m×n. Ma trận tổng C = A + B =
[cij]m×n; trong đó cij = aij + bij, i = 1, 2, . . . , m, j = 1, 2, . . . , n.
b. Phép nhân một ma trận với một số
Cho ma trận A = [aij]m×n và số thực k. Ma trận k.A = [k.aij]m×n, i = 1, 2, . . . , m, j =
1, 2, . . . , n.
Ví dụ.
A =
1 2 3
0 5 4
; B =
2 0 −4
3 −5 2
.
Ta có:
A + B =
3 2 −1
3 0 6
; 2A =
2 4 6
0 10 8
.
Ngô Mạnh Tưởng 3](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-7-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
c. Phép nhân một ma trận hàng với một ma trận cột
Giả sử u là ma trận cấp 1 × n, v là ma trận cấp n × 1,
u = u1 u2 ... un , v =
v1
v2
...
vn
.
Tích của u và v được xác định:
u · v = u1.v1 + u2.v2 + · · · + un.vn.
Điều kiện để thực hiện phép nhân hai ma trận:
Muốn nhân ma trận A với ma trận B thì số cột của A phải bằng số hàng của B.
d. Phép nhân hai ma trận
Cho A = [aik]m×p là ma trận cấp m × p, B = [bkj]p×n là ma trận cấp p × n. Ma trận
tích C = A.B = [cij]m×n là ma trận cấp m × n, trong đó mỗi phần tử của C được xác
định bằng (Hàng i của A) x (Cột j của B)
cij = ai1.b1j + ai2.b2j + · · · + aip.bpj, i = 1, 2, . . . , m, j = 1, 2, . . . , n.
Ví dụ. Cho các ma trận
A =
3 1 4
2 0 5
; B =
1 3 0 0
1 1 0 0
0 0 1 1
;
Tìm ma trận tích C = A.B C sẽ là ma trận cấp 2x4 với các phần tử được xác định:
c11 = 3 × 1 + 1 × 1 + 4 × 0 = 4;
c12 = 3 × 3 + 1 × 1 + 4 × 0 = 10;
c13 = 3 × 0 + 1 × 0 + 4 × 1 = 4;
c14 = 3 × 0 + 1 × 0 + 4 × 1 = 4;
c21 = 2 × 1 + 0 × 1 + 5 × 0 = 2;
c22 = 2 × 3 + 0 × 1 + 5 × 0 = 6;
c23 = 2 × 0 + 0 × 0 + 5 × 1 = 5;
c24 = 2 × 0 + 0 × 0 + 5 × 1 = 5.
hay
A.B =
3.1 + 1.1 + 4.0 3.3 + 1.1 + 4.0 3.0 + 1.0 + 4.1 3.0 + 1.0 + 4.1
2.1 + 0.1 + 5.0 2.3 + 0.1 + 5.0 2.0 + 0.0 + 5.1 2.0 + 0.0 + 5.1
=
4 10 4 4
2 6 5 5
.
Vậy ma trận tích
C =
4 10 4 4
2 6 5 5
.
Ngô Mạnh Tưởng 4](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-8-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
• Nếu các ma trận thỏa mãn điều kiện nhân: A là ma trận cấp m×p, B là ma trận loại
p×q, C là ma trận cấp q×n thì tích A.B.C có tính chất kết hợp: A.(B.C) = (A.B).C;
• Phép nhân hai ma trận không có tính chất giao hoán;
• Nếu A, B thỏa mãn điều kiện nhân thì At
, Bt
cũng thỏa mãn điều kiện nhân và ta
có (A.B)t
= Bt
.At
;
• Trong phép nhân hai ma trận, hệ thức A.B = 0 chưa chắc đã kéo theo hoặc A = 0,
hoặc B = 0;
• Tính chất của ma trận đơn vị: Mọi ma trận đơn vị I nhân với ma trận vuông A
cùng cấp ta luôn có I.A = A.I = A.
1.2. Định thức
1.2.1. Định nghĩa định thức
• Cho A = [aij]n×n là ma trận vuông cấp n. Định thức của ma trận A là một số, ký
hiệu là det(A) hoặc |A|.
• Ký hiệu Aij là định thức thu được từ A bằng cách bỏ đi hàng i cột j của ma trận
A, được gọi là định thức con của A.
• Phần bù đại số của phần tử aij là đại lượng: Aij = (−1)i+j
· Aij, i = 1, 2, . . . , n, j =
1, 2, . . . , n.
Định nghĩa 1.2.1. Tính định thức bằng quy nạp
1. Với k = 1, A = [a11] suy ra |A| = a11.
2. Với k = 2,
A =
a11 a12
a21 a22
suy ra |A| = a11 · a22 − a12 · a21 = a11 · A11 + a12 · A12.
3. Với k = 3,
A =
a11 a12 a13
a21 a22 a23
a31 a32 a33
suy ra |A| = a11A11 + a12A12 + a13A13.
Ngô Mạnh Tưởng 5](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-9-320.jpg)




















![Chương 2
HÀM SỐ MỘT BIẾN
Trong chương trình bày các khái niệm cơ bản về hàm số một biến; giới hạn, liên
tục của hàm số một biến. Giới thiệu một số mô hình hàm, ứng dụng của cấp số nhân
trong phân tích kinh tế.
2.1. Hàm số một biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.2. Giới hạn của dạy số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.3. Giới hạn của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.4. Hàm số liên tục. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.5. Các mô hình hàm số trong phân tích kinh tế . . . . . . . . . . . . . . . . . . 43
2.6. Ứng dụng của cấp số nhân trong phân tích kinh tế . . . . . . . . . . . . 46
2.7. BÀI TẬP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
2.1. Hàm số một biến
2.1.1. Định nghĩa
Định nghĩa 2.1.1. Cho tập hợp số thực R. Một ánh xạ f từ R vào R được gọi là một
hàm số thực của một biến số thực, hay hàm số của một biến số, trong đó
• Phần tử x được gọi là biến số độc lập. Phần tử y tương ứng với x được gọi là giá trị
của hàm số tại x, ký hiệu y = f(x);
• Miền xác định: D = {x ∈ R| ∃ f (x) };
• Miền giá trị: Y = {f (x)| x ∈ D }.
Ví dụ. Hàm số y =
√
9 − x2 có miền xác định là D = [−3; 3]; miền giá trị là Y = [0; 3].
2.1.2. Đồ thị của hàm số
Định nghĩa 2.1.2. Cho hàm số y = f(x) có miền giá trị D. Tập tất cả các điểm trên
mặt phẳng Oxy: G = {M (x, y)| x ∈ D, y = f (x)} được gọi là đồ thị của hàm số.](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-30-320.jpg)

![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Hình 2.3: Tính chất của đồ thị hàm ngược
3. Hàm mũ y = ax
; a > 0, a = 1;
4. Hàm logarit y = logax; (a > 0, a = 1);
5. Các hàm lượng giác;
6. Các hàm lượng giác ngược;
7. Các hàm hypebolic.
Định nghĩa 2.1.6. Hàm sơ cấp là hàm thu được từ các hàm sơ cấp cơ bản bằng cách sử
dụng hữu hạn các phép toán: Cộng, trừ, nhân, chia, khai căn và phép hợp.
2.1.5. Các hàm lượng giác ngược
a. Hàm lượng giác ngược của hàm số y = sin x
Xét hàm lượng giác y = sin x. Trên đoạn −π
2
; π
2
, y = sin x là hàm 1-1. Do đó tồn tại
hàm ngược, ký hiệu y = arcsin x.
Hàm arcsinx có miền xác định:[−1; 1]; miền giá trị −π
2
; π
2
và luôn đồng biến trên tập
xác định.
Ngô Mạnh Tưởng 28](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-32-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Hình 2.4: Đồ thị hàm sin và hàm arcsin x
b. Hàm lượng giác ngược của hàm số y = cos x
Xét hàm lượng giác y = cos x. Trên đoạn [0; π], y = cos x là hàm 1-1. Do đó tồn tại hàm
ngược, ký hiệu y = arccos x.
Hình 2.5: Đồ thị hàm cos và hàm arccos x
Hàm arccos x có miền xác định là[−1; 1]; miền giá trị [0; π] và luôn nghịch biến trên
miền xác định.
c. Hàm lượng giác ngược của hàm số y = tan x
Xét hàm lượng giác y = tan x. Trên khoảng −
π
2
;
π
2
, y = tan x là hàm 1-1. Do đó tồn
tại hàm ngược, ký hiệu y = arctan x.
Hình 2.6: Đồ thị hàm tan và hàm arctan x
Ngô Mạnh Tưởng 29](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-33-320.jpg)










![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
c. Khử các dạng vô định
Định lý 2.3.7. (Quy tắc ngắt bỏ VCL)
lim
x→x0
TonghuuhancacVCL
TonghuuhancacVCL
= lim
x→x0
VCLbaccaonhatcuatu
VCLbaccaonhatcuamau
.
Ví dụ. Tính
I = lim
x→+∞
√
x2 + 4 + 2x + 3
√
x
√
x2 − 4 + x
.
Tử là tổng của ba VCL:
√
x2 + 4 + 2x + 3
√
x
x→+∞
∼ 3x.
Mẫu là tổng của hai VCL:
√
x2 − 4 + x
x→+∞
∼ 2x
I = lim
x→+∞
3x
2x
=
3
2
.
2.4. Hàm số liên tục
2.4.1. Định nghĩa
Định nghĩa 2.4.1. (Hàm liên tục tại một điểm ) Hàm y = f(x) được gọi là liên tục tại
x0 nếu xác định tại điểm này và lim
x→x0
f(x) = f(x0).
Nếu hàm y = f(x) không liên tục tại điểm x0 ta nói hàm gián đoạn tại điểm x0.
Định nghĩa 2.4.2. (Hàm liên tục trên đoạn kín) Ta nói y = f(x) liên tục trên [a; b] nếu
f(x) liên tục tại mọi điểm x ∈ (a; b) và liên tục phải tại a ( lim
x→a+
f (x) = f (a)), liên tục
trái tại b ( lim
x→b−
f (x) = f (b)).
Ngô Mạnh Tưởng 40](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-44-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
2.4.2. Phân loại điểm gián đoạn
Cho x0 là điểm gián đoạn của hàm số y = f(x).
Điểm gián đoạn loại 1 x0 là điểm gián đoạn loại 1 nếu giới hạn trái (f (x0
−
)) và giới
hạn phải (f (x0
+
)) tồn tại hữu hạn.
x0 là điểm khử được nếu f (x0
−
) = f (x0
+
);
x0 là điểm nhảy nếu f (x0
−
) = f (x0
+
).
Điểm gián đoạn loại 2 Nếu một trong hai giới hạn một phía không tồn tại hoặc bằng
vô cùng.
2.4.3. Tính chất của hàm liên tục
Cho f (x) , g (x) là hai hàm liên tục tại x0. Khi đó:
1. αf(x); f(x) + g(x); f(x) · g(x) liên tục tại x0;
2. Nếu g(x) = 0 thì
f (x)
g (x)
liên tục tại x0.
Định lý 2.4.1. Nếu hàm f(x) liên tục tại x0 và f(x0) > 0 thì tồn tại một lân cận của
x0, sao cho f(x) > 0 với mọi x thuộc lân cận này.
Định lý 2.4.2. (Định lý Bozano - Cauchy) Nếu f(x) liên tục trên [a; b] và f(x) =
A; f(b) = B thì ∀C ∈ [a; b] tồn tại x0 ∈ [a; b] sao cho f(x0) = C.
Hệ quả 2.4.1. Nếu f(x) liên tục trên [a; b] và f(a).f(b) < 0 thì tồn tại x0 ∈ [a; b] sao
cho f(x0) = 0.
Định lý 2.4.3. Hàm sơ cấp liên tục trên tập xác định của nó.
Ngô Mạnh Tưởng 41](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-45-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Ví dụ. Khảo sát tính liên tục
f (x) =
sin x
x
, x = 0
1, x = 0.
∀x = 0, f(x) =
sin x
x
là hàm sơ cấp nên liên tục trên MXD.
Tại x = 0 : lim
x→0+
sin x
x
= 1 = lim
x→0−
sin x
x
= f(0).
Hàm liên tục tại x = 0. Vậy hàm liên tục trên R.
Ví dụ. Khảo sát tính liên tục
f(x) =
sin x
|x|
, x = 0
1, x = 0
∀x = 0, f(x) =
sin x
|x|
là hàm sơ cấp nên liên tục trên MXD.
Tại x = 0 : lim
x→0+
sin x
x
= 1; lim
x→0−
sin x
|x|
= −1
x = 0 là điểm nhảy.
Bước nhảy: h = f (0+
) − f (0−
) = 1 − (−1) = 2.
Ví dụ. Khảo sát điểm gián đoạn
f(x) = arctan
1
x
.
Tập xác định: Df = R {0}.
Tại x = 0 : lim
x→0+
arctan
1
x
=
π
2
, lim
x→0−
arctan
1
x
= −
π
2
x = 0 là điểm nhảy.
Bước nhảy: h = f (0+
) − f (0−
) = π
2
− (−π
2
) = π.
Ví dụ. Khảo sát điểm gián đoạn
f(x) = x arctan
1
x
.
Tập xác định: Df = R {0}.
Tại x = 0 : lim
x→0+
x arctan
1
x
= 0; lim
x→0−
x arctan
1
x
= 0
x = 0 là điểm gián đoạn khử được.
Ví dụ. Tìm a, b để hàm số liên tục trên [−π/2; 3π/2]
f(x) =
x cos(x/2)
sin x
, x ∈ [−π/2, 3π/2] , x = 0, x = π
a, x = 0
b, x = π
Ngô Mạnh Tưởng 42](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-46-320.jpg)
















![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
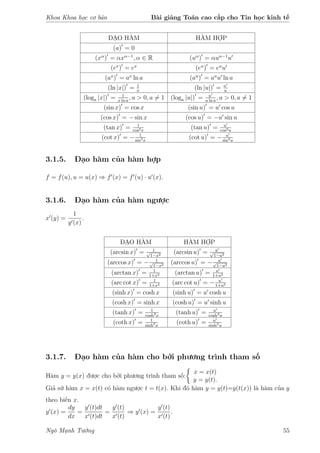
3.2.4. Vi phân cấp cao
Cho df (x) = f (x) dx là một hàm theo biến x. Vi phân (nếu có) của df(x) được gọi là vi
phân cấp 2 của hàm y = f(x) do đó
d2
f (x) = d (df) = d (f (x) dx) = (f (x) dx) dx = f (x) dx2
.
Tương tự, vi phân cấp n là vi phân (nếu có) của vi phân cấp n − 1
dn
f(x) = f(n)
(x)dxn
.
3.2.5. Vi phân cấp cao của hàm hợp
Cho hàm hợp
f = f(u)
u = u(x)
Vi phân cấp 1 có tính bất biến: df = f (x)dx = f (u)du.
Vi phân cấp 2: d2
f = d (df) = d (f (u)du).
Chú ý. dx là hằng số, du không phải là hằng số: du = u (x)dx
d2
f = d (f (u))×du+f (u)×d(du) = (f (u)) (u)du×du+f (u)×d2
u = f (u)du2
+f (u)d2
u.
3.3. Ứng dụng của đạo hàm của hàm số một biến
3.3.1. Các định lý về hàm số khả vi
Định lý 3.3.1. (Định lý Rolle) Nếu hàm f(x) liên tục trên khoảng kín [a, b]; khả vi
trong khoảng (a, b); f(a) = f(b) thì trong khoảng mở (a, b) có ít nhất một điểm c sao cho
f (c) = 0.
Chứng minh xem [1], [2], [5].
Định lý 3.3.2. (Định lý Lagrange) Nếu hàm f(x) liên tục trên khoảng kín [a, b], khả vi
trên khoảng mở (a, b) thì trong khoảng (a, b) có ít nhất một điểm c sao cho f (b) − f (a) =
f (c) (b − a).
Chứng minh xem [1], [2], [5].
Định lý 3.3.3. (Định lý Cauchy) Nếu các hàm f(x), g(x) liên tục trên [a, b], khả vi trong
(a, b) , g (x) = 0, ∀x ∈ (a, b), thì có ít nhất một điểm c ∈ (a, b) sao cho:
f (b) − f (a)
g (b) − g (a)
=
f (c)
g (c)
.
Ngô Mạnh Tưởng 60](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-64-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Để chứng minh định lý Cauchy ta áp dụng định lý Rolle cho hàm phụ
F(x) = f(x) −
f (b) − f(a)
g (b) − g(a)
[g(x) − g(a)] .
Định lý Lagrange là một trường hợp đặc biệt của định lý Cauchy với g(x) = x.
3.3.2. Quy tắc Lopitan
Định lý 3.3.4. Giả sử các hàm f(x), g(x) liên tục và khả vi trong một miền nào đó và
khi x → a hoặc khi x → ∞ thì cả hai hàm f(x), g(x) cùng tiến tới không (hoặc cùng tiến
tới vô cùng). Khi đó nếu giới hạn của tỷ số f (x)
g (x)
tồn tại thì giới hạn của tỷ số f(x)
g(x)
cũng
tồn tại và
lim
x→a
f (x)
g (x)
= lim
x→a
f (x)
g (x)
, lim
x→∞
f(x)
g(x)
= lim
x→∞
f (x)
g (x)
.
Chứng minh xem [1], [2], [5].
Quy tắc Lopitan có ứng dụng quan trọng trong việc tính toán các giới hạn có dạng vô
định 0
0
; ∞
∞
.
Ví dụ. Tính các giới hạn
1. lim
x→0
e2x−1−2x
2x2 = lim
x→0
2e2x−2
4x
= lim
x→0
4e2x
4
= 1.
2. lim
x→+∞
ln x
xα = lim
x→+∞
1
x
αxα−1 = lim
x→+∞
1
αxα = 0 (α > 0).
3. lim
x→+∞
ax
xn = lim
x→+∞
ax ln a
nxn−1 = ... = lim
x→+∞
ax(ln a)n
n!
= ∞ (a > 1).
Chú ý: Khi gặp các dạng vô định 0.∞, ∞ − ∞, 1∞
, 0∞
, 00
, ∞0
ta tìm cách biến đổi để
đưa chúng về dạng 0
0
; ∞
∞
rồi áp dụng quy tắc Lopitan.
Ví dụ. lim
x→0
(x2
ln x) = lim
x→0
ln x
1/x2
= lim
x→0
1/x
−2/x2 = −1
2
lim
x→0
x2
= 0.
3.3.3. Khai triển Taylor, Mac Laurin
Định lý 3.3.5. Nếu hàm số f(x) có đạo hàm liên tục tới cấp n trong một miền chứa
điểm x0 thì
f(x) = f (x0) +
f (x0)
1!
(x − x0) +
f (x0)
2!
(x − x0)2
+ · · · +
f(n)
(x0)
n!
(x − x0)n
+ Rn,
trong đó Rn được gọi là phần dư thứ n.
Ngô Mạnh Tưởng 61](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-65-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Công thức trên được gọi là công thức khai triển Taylor đến cấp n của hàm số bất f(x)
thành đa thức tại x0. Chứng minh xem [1], [2], [5].
Đặc biệt nếu x0 = 0 ta có công thức khai triển Mac Laurin
f(x) = f (0) +
f (0)
1!
x +
f (0)
2!
x2
+ ... +
f(n)
(0)
n!
xn
+ Rn
cho phép khai triển một hàm bất kì (có đạo hàm liên tục tới cấp n) thành đa thức của x.
Kết quả khai triển Mac Laurin của một số hàm số sơ cấp:
1. ex
= 1 + x
1!
+ x2
2!
+ ... + xn
n!
+ Rn.
2. sin x = x − x3
3!
+ x5
5!
− ... + (−1)k−1 x2k−1
(2k−1)!
+ R2k−1.
3. cos x = x − x2
2!
+ x4
4!
− ... + (−1)k x2k
(2k)!
+ R2k.
3.3.4. Bài toán khảo sát hàm số
Xem tài liệu [1], [2], [5].
3.4. Sử dụng đạo hàm trong phân tích kinh tế
3.4.1. Đạo hàm và giá trị cận biên
Xét mô hình hàm số: y = f(x), trong đó x và y là các biến số kinh tế. Trong kinh
tế học người ta quan tâm đến xu hướng biến thiên của y tại một điểm x0 khi x thay đổi
một lượng nhỏ. Theo định nghĩa đạo hàm ta có:
f (x0) = lim
∆x→0
f (x0 + ∆x) − f (x0)
∆x
.
Khi ∆x có giá trị tuyệt đối đủ nhỏ, ta có:
f (x0) ≈
f (x0 + ∆x) − f (x0)
∆x
⇒ ∆y = f (x0 + ∆x) − f (x0) ≈ f (x0) ∆x.
Khi ∆x = 1 ta có ∆y ≈ f (x0). Như vậy đạo hàm f (x0) biểu diễn xấp xỉ lượng thay đổi
giá trị của y khi x tăng thêm 1 đơn vị tại điểm x0. Giá trị này được gọi là giá trị y- cận
biên của x tại điểm x0.
Đối với một số hàm kinh tế, giá trị cận biên có tên gọi cụ thể như sau:
• Mô hình hàm sản xuất ngắn hạn Q = f(L), f (L0) được gọi là sản phẩm hiện vật
cận biên tại điểm L0. Giá trị này được ký hiệu là MPPL (Marginal Physical Product
Ngô Mạnh Tưởng 62](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-66-320.jpg)







![Chương 4
TÍCH PHÂN
Trong chương trình bày một số khái niệm cơ bản về nguyên hàm, tích phân, các
phương pháp tính tích phân của các hàm số hữu tỷ, vô tỷ, lượng giác; tích phân xác định,
tích phân suy rộng, các phương pháp tính và xét sự hội tụ của tích phân suy rộng; Ứng
dụng của tích phân trong phân tích kinh tế.
4.1. Nguyên hàm và tích phân không xác định. . . . . . . . . . . . . . . . . . . . . 70
4.2. Phương pháp tính tích phân không xác định . . . . . . . . . . . . . . . . . . 72
4.3. Phép tính nguyên hàm của một số hàm số . . . . . . . . . . . . . . . . . . . . 73
4.4. Tích phân xác định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
4.5. Hai phương pháp tính tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
4.6. Tích phân suy rộng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
4.7. Ứng dụng tích phân trong phân tích kinh tế . . . . . . . . . . . . . . . . . . 93
4.8. BÀI TẬP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
4.1. Nguyên hàm và tích phân không xác định
4.1.1. Nguyên hàm của hàm số một biến
Định nghĩa 4.1.1. Cho hàm số y = f(x) xác định trong khoảng mở (a; b)
Hàm số y = F(x) xác định trong (a; b) được gọi là nguyên hàm của hàm số y = f(x)
nếu y = F(x) có đạo hàm tại mọi điểm thuộc (a; b) và F (x) = f(x) hay dF(x) = f(x)dx
với mọi x ∈ (a; b).
• Hai nguyên hàm khác nhau của cùng một hàm số chỉ sai khác nhau một hằng số.
• Hàm số y = F(x) là nguyên hàm của hàm số y = f(x) trên khoảng đóng [a; b] nếu
– F(x) là nguyên hàm của f(x) trên (a; b) ;
– F (a + 0) = f(a); F (b − 0) = f(b).
Ví dụ. Nguyên hàm của hàm số f(x) = x2
là hàm số F(x) =
x3
3
. Nguyên hàm của hàm
số f(x) = sinx là hàm số F(x) = −cosx.](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-74-320.jpg)

![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
4.2. Phương pháp tính tích phân không xác định
4.2.1. Phương pháp đổi biến số
Định nghĩa 4.2.1. Nếu tồn tại hàm hợp f(ϕ(x)) và hàm t = ϕ(x) liên tục trên đoạn
[a; b] và khả vi trong khoảng (a; b), thì
f(ϕ(x)) · ϕ (x)dx = f(t)dt
t=ϕ(x)
.
Nếu tồn tại hàm số ngược x = ϕ−1
(t) của hàm t = ϕ(x) thì
f(t)dt = f(ϕ(x))ϕ (x)dx
x=ϕ−1(t)
hay
f(x)dx = f(ϕ(t))ϕ (t)dt
t=ϕ−1(x)
.
Ví dụ. Tính I =
dx
sin x
. Ta có
I =
dx
sin x
=
sin xdx
sin2
x
= −
dcosx
1 − cos2x
= −
dt
1 − t2
=
1
2
dt
t − 1
−
dt
t + 1
=
1
2
ln
cosx − 1
cosx + 1
+ C =
1
2
ln tan
x
2
+ C.
Ví dụ. Tính
ln(arccos x)dx
√
1 − x2 arccos x
. Đặt t = ln(arccos x) ⇒ dt =
−dx
√
1 − x2 arccos x
. Suy ra
ln(arccos x)dx
√
1 − x2 · arccos x
=
1
2
ln2
(arccos x) + C.
Ví dụ. Tính
dx
a2 + x2
bằng phương pháp đổi biến.
Sử dụng đổi biến dạng (2) đặt x = atant, a2
+ x2
=
a2
cos2t
, dx = a.
dt
cos2t
dx
a2 + x2
=
a.dt
cos2 t
:
a2
cos2 t
=
1
a
dt =
1
a
t + C =
1
a
arctan
x
a
+ C.
Chú ý. Thông thường khi gặp biểu thức
√
a2 − x2 đặt x = a sin t; khi gặp biểu thức
1
a2 + x2
đặt x = arctan x và sử dụng phép đổi biến số dạng (2).
4.2.2. Phương pháp tích phân từng phần
Định nghĩa 4.2.2. Giả sử hai hàm u = u(x), v = v(x) liên tục trên [a; b] và khả vi trong
(a; b). Nếu tồn tại v.u dx thì tồn tại u.v dx. Ngoài ra u · v dx = u · v − v · u dx hay
u · dv = u · v − v · du.
Ngô Mạnh Tưởng 72](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-76-320.jpg)







![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Hình dưới là các trường hợp chia S thành 8 và 12 phần
Với n càng lớn, diện tích tính được càng chính xác
Trên mỗi miền con S1, S2, ..., Sn lấy một điểm tùy ý Ta có S = S1 + S2 + · · · + Sn
S f (x∗
1) (x1 − x0) + f (x∗
2) (x2 − x1) + · · · f (x∗
n) (xn − xn−1)
S
n
i=1
f (x∗
i ) ∆xi
Nếu giới hạn I = lim
∆xi→0
n
i=1
f (x∗
i ) ∆xi tồn tại không phụ thuộc cách chia S và cách
chọn điểm x∗
i , thì I được gọi là tích phân xác định của hàm y = f(x) trên đoạn [a, b] và
S = lim
max(∆xi)→0
n
i=1
f (x∗
i ) ∆xi =
b
a
f (x)dx.
Ví dụ. Tính diện tích S giới hạn bởi: đường cong y = x2
, trục hoành, hai đường thẳng
x = 0 và x = 1
Chia S thành 4 miền và chọn điểm trung gian bên trái
Ngô Mạnh Tưởng 80](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-84-320.jpg)

![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Chia S thành 30 miền và chọn điểm trung gian bên trái, bên phải
Chia S thành 50 miền và chọn điểm trung gian bên trái, bên phải
Bảng thống kê một số giá trị
4.4.2. Tính chất
1. Nếu các hàm f(x), g(x) khả tích trên [a, b] thì các hàm f(x) + g(x), k.f(x) với k là
hằng số cũng khả tích trên [a, b] và
b
a
[f(x) + g(x)]dx =
b
a
f(x)dx +
b
a
g(x)dx;
b
a
kf(x)dx = k
b
a
f(x)dx;
2. Nếu hàm f khả tích trên các đoạn [a, c], [c, b] thì nó cũng khả tích trên [a, b] và
b
a
f(x)dx =
c
a
f(x)dx +
b
c
f(x)dx;
Ngô Mạnh Tưởng 82](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-86-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
3. Nếu f (x) 0, ∀x ∈ [a, b] thì
b
a
f (x) dx 0;
4. Nếu f (x) g (x) , ∀x ∈ [a, b] thì
b
a
f(x)dx
b
a
g(x)dx;
5. Nếu m và M là giá trị nhỏ nhất và lớn nhất của hàm f(x) trên [a, b] thì
m(b − a)
b
a
f(x)dx M(b − a);
6. Nếu f(x) là hàm lẻ thì
a
−a
f(x)dx = 0.
Nếu f(x) là hàm chẵn thì
a
−a
f(x)dx = 2
a
0
f(x)dx;
7. Công thức Newton- Leibnitz: Cho hàm số y = f(x) liên tục trên [a, b] và có nguyên
hàm là F(x). Khi đó
b
a
f(x)dx = F(x)|b
a = F(b) − F(a);
8. Công thức đạo hàm theo cận trên: Nếu f(x) liên tục trên [a, b] thì
x
a
f(t)dt
= f(x)
ϕ(x)
a
f(t)dt
= f(x).ϕ (x).
4.5. Hai phương pháp tính tích phân
4.5.1. Phương pháp đổi biến số
Nếu f(x) là một hàm liên tục trên [a, b], x = ϕ(t) là một hàm xác định và có đạo hàm
liên tục trên [α, β] với ϕ(α) = a, ϕ(β) = b thì
b
a
f(x)dx =
β
α
f[ϕ(t)].ϕ (t)dt.
Ví dụ. Tính I =
a
0
√
a2 − x2dx
Giải: Phép đổi biến x = a sin x ta có:
a2
− x2
= a2
(1 − sin2
t) = a2
cos2
t, dx = a cos tdt.
Ngô Mạnh Tưởng 83](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-87-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Đổi cận x = 0 ⇒ t = 0, x = a ⇒ t =
π
2
. Do đó
I =
π/2
0
a cos t.a cos tdt = a2
π/2
0
cos2
tdt =
a2
2
π/2
0
(1 + cos 2t)dt
=
a2
2
t +
1
2
sin 2t
π/2
0
=
πa2
4
.
Ví dụ. Tính I =
π/2
0
sin x
1 + cos2x
dx.
Giải: Đặt t = cos x ⇒ dt = − sin xdx, đổi cận x = 0 ⇒ t = 1, x =
π
2
⇒ t = 0
I =
0
1
−dt
1 + t2
=
1
0
dt
1 + t2
= arctgt|1
0 =
π
4
.
4.5.2. Phương pháp tích phân từng phần
Nếu u và v là các hàm số cùng với các đạo hàm của chúng liên tục trên [a, b] thì
b
a
f (x) dx =
b
a
udv = uv|b
a −
b
a
vdu.
Thật vậy, uv|b
a =
b
a
d(uv) =
b
a
(vdu + udv) =
b
a
vdu +
b
a
udv.
Ví dụ. Tính I =
2
1
ln xdx.
Giải: Đặt u = ln x, dv = dx ta có du =
dx
x
, v = x suy ra
I = x ln x |2
1 −
2
1
dx = 2 ln 2 − 1.
4.6. Tích phân suy rộng
4.6.1. Tích phân suy rộng loại 1 (Cận lấy tích phân là vô hạn)
a. Bài toán
Tính diện tích S miền vô hạn giới hạn bởi: đường cong y = f(x) ≥ 0 , trục hoành,
đường thẳng x = a
S =
+∞
a
f (x) dx = lim
b→+∞
b
a
f (x) dx.
Ngô Mạnh Tưởng 84](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-88-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
b. Định nghĩa
Định nghĩa 4.6.1. Cho hàm số y = f(x) khả tích trên đoạn [a, b], với mọi b > a.
Tích phân
+∞
a
f (x) dx = lim
b→+∞
b
a
f (x) dx
được gọi là tích phân suy rộng loại 1.
Các tích phân sau cũng được gọi là tích phân suy rộng loại 1
a
−∞
f (x) dx = lim
b→−∞
a
b
f (x) dx
+∞
−∞
f (x) dx =
a
−∞
f (x) dx +
+∞
a
f (x) dx.
c. Sự hội tụ, phân kỳ của tích phân suy rộng loại 1
Định nghĩa 4.6.2. Nếu giới hạn lim
b→+∞
b
a
f (x) dx tồn tại hữu hạn thì tích phân
+∞
a
f (x) dx
được gọi là hội tụ. Ngược lại, nếu tích phân không tồn tại hoặc bằng vô cùng thì tích
phân gọi là phân kỳ.
Định lý 4.6.1. (Công thức Newton-Leibnitz ) Giả sử F(x) là nguyên hàm của hàm số
f(x) trên [a, +∞) khi đó
+∞
a
f(x)dx = lim
b→+∞
b
a
f(x)dx = lim
b→+∞
(F(b) − F(a)) .
Tích phân tồn tại khi và chỉ khi tồn tại lim
b→+∞
F(b) := F(∞)
+∞
a
f(x)dx = F(x)|+∞
a = F(+∞) − F(a).
Ngô Mạnh Tưởng 85](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-89-320.jpg)

![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
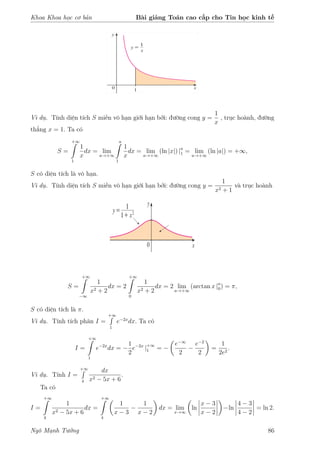
3. Với α = 1, suy ra
+∞
a
1
x
dx = ln |x||+∞
a = +∞
nên tích phân phân kỳ.
Vậy tích phân I =
+∞
a
1
xα
dx (α > 0) hội tu khi α > 1 và phân kỳ khi α 1.
d. Các tiêu chuẩn hội tụ
Định lý 4.6.2. (Định lý so sách 1) Giả sử các hàm số f (x) , g (x) khả tích trên [a, b] và
0 f (x) g (x) , x a. Khi đó
1. Nếu
+∞
a
g (x) dx hội tụ thì
+∞
a
f (x) dx hội tụ;
2. Nếu
+∞
a
f (x) dx phân kỳ thì
+∞
a
g (x) dx phân kỳ.
Để khảo sát sự hội tụ của I =
+∞
a
f(x)dx thường so sánh với
+∞
a
dx
xα
đã biết kết quả.
Chú ý. Trong định lý so sánh 1
1. f (x) , g (x) là các hàm số không âm;
2. Chỉ cần tồn tại α sao cho α a (∀x ∈ [α, +∞)) f(x) g(x);
3. Cận dưới của tích phân
+∞
a
dx
xα
là số dương a > 0.
Ví dụ. Khảo sát sự hội tụ của tích phân I =
+∞
1
dx
2x2 + sin2
3x
.
Ta có f(x) =
1
2x2 + sin2
3x
1
2x2
= g(x). Vì
+∞
1
dx
2x2
hội tụ, theo định lý so sánh 1 suy
ra I hội tụ.
Ví dụ. Khảo sát sự hội tụ của tích phân I =
+∞
1
ln3
xdx
x + 5
.
Ta có f (x) =
ln3
x
x + 5
>
1
x + 5
>
1
2x
= g (x) , ∀x > 5. Vì
+∞
1
dx
2x
phân kỳ, theo định lý so
sách 1 suy ra I phân kỳ.
Định lý 4.6.3. (Định lý so sách 2) Giả sử các hàm số f (x) , g (x) không âm, khả tích
trên [a, b] và lim
x→+∞
f (x)
g (x)
= k. Khi đó
• Nếu 0 < k < +∞ thì các tích phân
+∞
a
f (x) dx và
+∞
a
g (x) dx cùng hội tụ hay cùng
phân kỳ;
Ngô Mạnh Tưởng 88](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-92-320.jpg)

![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Do
+∞
1
1
x2
dx hội tụ, do đó J hội tụ. Áp dụng định lý suy ra I hội tụ tuyệt đối.
Chú ý.
1. Các tích phân
a
−∞
f (x) dx,
+∞
−∞
f (x) dx cũng có kết quả tương tự.
2. Với các tích phân chỉ có một điểm suy rộng
+∞
a
f(x)dx khi tách có dạng vô định
G(x)|+∞
a + H(x)|+∞
a = ∞ − ∞ chưa kết luận được tích phân ban đầu phân kỳ.
3. Với tích phân có hai điểm suy rộng
+∞
−∞
f (x) dx khi tách ra thành các tích phân
a
−∞
f(x)dx +
+∞
a
f(x)dx chỉ cần một trong hai tích phân phân kỳ thì tích phân ban
đầu phân kỳ.
4.6.2. Tích phân suy rộng loại 2 (Hàm dưới dấu tích phân có
điểm gián đoạn vô cực trong khoảng lấy tích phân)
a. Định nghĩa
Định nghĩa 4.6.4. Điểm x0 được gọi là điểm bất thường (hay điểm kỳ dị) của đường
cong y = f(x) nếu lim
x→x0
f(x) = ∞.
Giả sử trên [a, b] hàm số y = f(x) có một điểm bất thường duy nhất là x0 = b
Khi đó
b
a
f(x)dx := lim
t→0
b−t
a
f(x)dx
(0 < t < b − a) được gọi là tích phân suy
rộng loại hai của f(x) trên [a, b].
Giả sử trên [a, b] hàm số y = f(x) có một điểm bất thường duy nhất là x0 = a
Khi đó tích phân suy rộng loại hai của
f(x) trên [a, b] là
b
a
f(x)dx := lim
t→0
b
a+t
f(x)dx
trong đó (0 < t < b − a).
Ngô Mạnh Tưởng 90](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-94-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
Giả sử trên [a, b] hàm số y = f(x) có một điểm bất thường duy nhất là c ∈ [a, b]
Khi đó tích phân suy rộng loại hai của
f(x) trên [a, b] là
b
a
f(x)dx =
c
a
f(x)dx +
b
c
f(x)dx
= lim
t→0
c−t
a
f(x)dx + lim
t→0
b
c+t
f(x)dx.
Tích phân vế trái là hội tụ khi và chỉ khi cả hai tích phân ở vế phải hội tụ.
Nhận xét.
1. Các khái niệm hội tụ, phân kỳ giống như trong tích phân suy rộng loại một.
2. Tương tự tích phân suy rộng loại một: có hai tiêu chuẩn so sánh cho tích phân hàm
không âm.
3. Khái niệm hội tụ tuyệt đối cũng tương tự trong tích phân suy rộng loại một: Hội
tụ tuyệt đối thì hội tụ.
Ví dụ. Tính I =
0
−1
dx
√
1 − x2
.
Giải: Ta có điểm x = −1 là điểm bất thường nên
I =
0
−1
dx
√
1 − x2
= lim
ε→0
0
−1+ε
dx
√
1 − x2
= lim
ε→0
arcsin x |0
−1+ε
= lim
ε→0
(− arcsin (−1 + ε)) =
π
2
.
Ví dụ. Tính tích phân I =
3
0
dx
x − 1
.
Giải: Ta có điểm x = 1 là điểm bất thường trên [0, 3] nên
I =
1
0
dx
x − 1
+
3
1
dx
x − 1
= I1 + I2.
Mặt khác do
I1 = lim
t→0
1−t
0
dx
x − 1
= lim
t→0
ln |x − 1| |1−t
0 = lim
t→0
ln |t| = +∞.
Vậy I phân kỳ.
Ví dụ. Xét sự hội tụ của tích phân I =
b
a
1
(b − x)α dx (a < b, α > 0).
Giải: Ta có x = b là điểm bất thường
Ngô Mạnh Tưởng 91](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-95-320.jpg)
![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
• Với α = 1 ta có
I = lim
ε→0
b−ε
a
1
(b − x)α dx = lim
ε→0
(b − x)1−α
α − 1
|b−ε
a =
= lim
ε→0
1
α − 1
ε1−α
+
1
1 − α
(b − a)1−α
=
+∞ khi α > 1
(b − a)1−α
1 − α
khi α < 1.
• Với α = 1 ta có
b
a
1
(b − x)α dx =
b
a
1
b − x
dx = − lim
ε→0
ln |b − x| |b−ε
a = −∞.
• Vậy I hội tụ khi α < 1, phân kỳ khi α ≥ 1.
Ví dụ. Tương tự tích phân I =
b
a
1
(x − a)α dx (a < b, α > 0) hội tụ khi α < 1, phân kỳ
khi α ≥ 1.
b. Các tiêu chuẩn hội tụ
Định lý 4.6.4. (Định lý so sách 1) Giả sử các hàm số f (x) , g (x) khả tích trên (a, b] với
x = a là điểm bất thường duy nhất sao cho 0 ≤ f (x) ≤ g (x) , ∀x ∈ (a, c] ; a < c < b . Khi
đó
1. Nếu
b
a
g (x) dx hội tụ thì
b
a
f (x) dx hội tụ;
2. Nếu
b
a
f (x) dx phân kỳ thì
b
a
g (x) dx phân kỳ.
Định lý 4.6.5. (Định lý so sách 2) Giả sử các hàm số f (x) , g (x) không âm, khả tích
trên (a, b] với x = a là điểm bất thường duy nhất và lim
x→a+
f (x)
g (x)
= k. Khi đó
• Nếu 0 < k < +∞ thì các tích phân
b
a
f (x) dx và
b
a
g (x) dx cùng hội tụ hay cùng
phân kỳ;
• Nếu k = 0 và tích phân
b
a
g (x) dx hội tụ thì tích phân
b
a
f (x) dx hội tụ;
• k = +∞ và tích phân
b
a
g (x) dx phân kỳ thì tích phân
b
a
f (x) dx phân kỳ.
Định nghĩa 4.6.5. Giả sử hàm số f (x) có dấu bất kỳ. Khi đó
• Nếu
b
a
|f (x)| dx hội tụ thì
b
a
f (x) dx hội tụ và được gọi
b
a
f (x) dx hội tụ tuyệt đối;
Ngô Mạnh Tưởng 92](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-96-320.jpg)



![Khoa Khoa học cơ bản Bài giảng Toán cao cấp cho Tin học kinh tế
4.7.2. Ứng dụng tích phân xác định
a. Tính xác suất
Xét biến số x nhận các giá trị bằng số khác nhau một cách ngẫu nhiên, gọi là biến
ngẫu nhiêu. Xác suất để biến ngẫu nhiên x nhận một giá trị x0 nào đó được tính thông
qua một hàm số gọi là hàm mật độ xác suất hay hàm xác suất. Hàm mật độ xác suất của
một biến ngẫu nhiên liên tục x là một hàm số liên tục f(x) thỏa mãn các điều kiện sau:
1. f (x) ≥ 0 (có xác suất là số không âm);
2. Nếu miền biến thiên của biến số x là đoạn [A; B] thì
B
A
f (x) dx = 1;
3. Xác suất để x nhận giá trị trong đoạn [a; b] được tính bởi công thức
P (a ≤ x ≤ b) =
b
a
f (x) dx (A ≤ a ≤ b ≤ B) .
Ví dụ. Gọi t là thời gian xếp hàng để mua hàng trong một cửa hàng lớn (đo bằng phút).
Qua số liệu thực nghiệm người ta ước lượng được hàm tần suất
f(t) =
4
81
t3
(0 ≤ t ≤ 3).
Xác suất để một khách hàng phải xếp hàng từ 1 đến 2 phút là
p =
2
1
4
81
t3
dt =
1
81
t4 2
1
=
15
81
.
b. Tính thặng dư của người tiêu dùng và thặng dư của nhà sản xuất
Khái niệm hàm cung, hàm cầu và điểm cân bằng thị trường đã được trình bày ở
chương 2. Thông qua mô hình thị trường người ta có thể đánh giá được lợi ích của thị
trường đối với cả người mua và người bán.
Trong mô hình thị trường, hàm cầu Qd = D(p) cho biết lượng hàng hóa Qd mà người
mua bằng lòng mua ở mỗi mức giá p (Qd là lượng cầu của toàn bộ thị trường). Khi biểu
diễn bằng đồ thị mối liên hệ giữa giá và lượng cầu, các nhà kinh tế thường sử dụng trục
tung để biểu diễn giá p và trục hoành biểu diễn lượng Q. Với cách biểu diễn như vậy thì
đường cầu là đồ thị của hàm cầu đảo p = D−1
(Qd) (hàm ngược của hàm cầu Qd = D(p)).
Giả sử điểm cân bằng thị trường là (p0, Q0) và hàng hóa được bán với giá p0 trên thị
Ngô Mạnh Tưởng 96](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-100-320.jpg)




![Tài liệu tham khảo
[1] Lê Đình Thúy(2007), Toán cao cấp cho các nhà kinh tế, phần 1, 2, NXB Đại học
Kinh tế Quốc dân.
[2] Trương Hà Hải, Đàm Thanh Phương và nhóm tác giả (2016), Toán học cao cấp 1,
NXB Đại học Thái Nguyên.
[3] Trần Trọng Huệ (2001), Đại số tuyến tính và hình giải tích, NXB ĐH Quốc gia Hà
Nội.
[4] Lê Ngọc Lăng (2003), Bài tập và luyện tập Toán cao cấp, tập 1,2, NXB ĐHSP.
[5] Nguyễn Đình Trí, Tạ Văn Đĩnh, Nguyễn Hồ Quỳnh(2002), Toán học cao cấp, Tập
1,2. NXB Giáo dục.
[6] Nguyễn Đình Trí, Tạ Văn Đĩnh, Nguyễn Hồ Quỳnh(2002), Bài tập Toán học cao cấp,
Tập 1,2. NXB Giáo dục.
101](https://image.slidesharecdn.com/baigiangtoankt-170901075422/85/Bai-gi-ng-Toan-kinh-t-105-320.jpg)