Tài liệu gồm nhiều bài toán toán kinh tế liên quan đến sản lượng, chi phí và mô hình cung cầu. Các câu hỏi yêu cầu tính toán sản lượng cận biên, chi phí sản xuất, giá sản phẩm và các chỉ số kinh tế khác. Đặc biệt, tài liệu sử dụng các ma trận và phương pháp tính toán phức tạp để phân tích tình hình kinh tế trong các ngành sản xuất.








![9
Câu 1: Cho MTHSCPTT dạng hiện vật 3 ngành:
𝜶 = [
𝟎, 𝟐 𝟎, 𝟏 𝟎, 𝟑
𝟎, 𝟒 𝟎, 𝟑 𝟎, 𝟏
𝟎, 𝟏 𝟎, 𝟑 𝟎, 𝟐
]
𝜽 = (𝑬 − 𝜶)−𝟏
= [
𝟏, 𝟓𝟗 𝟎, 𝟓𝟏 𝟎, 𝟔𝟔
𝟎, 𝟗𝟗 𝟏, 𝟖𝟑 𝟎, 𝟔𝟎
𝟎, 𝟓𝟕 𝟎, 𝟕𝟓 𝟏, 𝟓𝟔
]
Vecto hệ số sử dụng lao động 𝜷 = (𝟎, 𝟐 𝟎, 𝟑 𝟎, 𝟏)
1. Nêu ý nghĩa của 𝛼31, 𝜃31, giải thích sự khác nhau giữa chúng
𝛼31 = 0,1 : Cho biết ngành 1 muốn sản xuất ra 1 đơn vị sản phẩm thì ngành
3 phải cung cấp cho nó 0,1 đơn vị sản phẩm
𝜃31 = 0,57: Cho biết ngành 1 muốn sản xuất ra 1 đơn vị sản phẩm cuối cùng
thì ngành 3 phải sản xuất cho nó 0,57 đơn vị sản phẩm
𝑆ự 𝑘ℎá𝑐 𝑛ℎ𝑎𝑢 𝑔𝑖ữ𝑎 𝑐ℎú𝑛𝑔:
2. Biết nhu cầu SPCC của 3 ngành lần lượt là: 190, 280, 330 đơn vị. Tính sản
lượng và số lao động phải sử dụng của mỗi ngành
Theo giả thiết, ta có SPCC của 3 ngành:
𝑞 = (190 280 330)
𝑄 = 𝜃. 𝑞
= (
1,59 0,51 0,66
0,99 1,83 0,6
0,57 0,75 1,56
) . (
190
280
330
) = (
662,7
898,5
833,1
)
Lượng lao động phải sử dụng mỗi ngành là
𝑄01 = 𝛽1. 𝑄1 = 0,2 𝑥 662,7 = 132,54
𝑄02 = 𝛽2. 𝑄2 = 0,3 𝑥 898,5 = 269,55
𝑄03 = 𝛽3. 𝑄3 = 0,1 𝑥 833,1 = 83,31
3. Cho tiền công của 3 ngành lần lượt là: 19, 28, 30 đơn vị](https://image.slidesharecdn.com/thitonkinhtccnm-220508125302-c96a3169/85/D-THI-TOAN-KINH-T-CAC-NAM-pdf-9-320.jpg)











![21
Xét hệ phương trình: {{
𝜋′𝑄1
= −4𝑄1 + 2𝑄2 + 24 = 0
𝜋𝑄2
= −6𝑄2 + 2𝑄1 + 78 = 0
=> {
𝑄1 = 15
𝑄2 = 18
M(𝑄1 = 15, 𝑄2 = 18) là điểm dừng
+) Điều kiện đủ:
𝑎11 = 𝜋′′𝑄1
=
𝜕𝜋
𝜕𝑄1
2 = −4
𝑎22 = 𝜋′′𝑄2
=
𝜕𝜋
𝜕𝑄2
2 = −6
𝑎12 = 𝑎21 = 𝜋′𝑄1𝑄2
=
𝜕𝜋
𝜕𝑄1
𝜕𝑄2
= 2
Tính:
𝐷 = |
−4 2
2 −6
| = 20 > 0
Vậy M(𝑄1 = 15, 𝑄2 = 18) thì lời nhuận tối đa
Khi đó:
𝑃1 = 24 − 𝑄1 + 𝑄2 = 27
𝑃2 = 78 + 𝑄1 − 2𝑄2 = 57
Câu 3: Cho biết các ma trận hệ số chi phí dạng hiện vật, của 3 ngành:
𝜶 = [
𝟎, 𝟒 𝟎, 𝟐 𝟎, 𝟑
𝟎, 𝟏 𝟎, 𝟏 𝟎, 𝟎𝟓
𝟎, 𝟐 𝟎, 𝟐 𝟎, 𝟏
]
𝜽 = [
𝟐, 𝟎 𝟎, 𝟔 𝟎, 𝟕
𝟎, 𝟐𝟓 𝟏, 𝟐 𝟎, 𝟏𝟓
𝟎, 𝟓 𝟎, 𝟒 𝟏, 𝟑
]
𝜷 = (𝟎, 𝟐 𝟎, 𝟏 𝟎, 𝟐)](https://image.slidesharecdn.com/thitonkinhtccnm-220508125302-c96a3169/85/D-THI-TOAN-KINH-T-CAC-NAM-pdf-21-320.jpg)




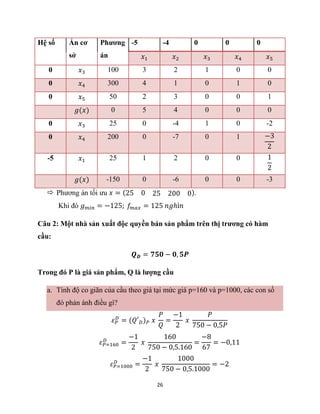















![45
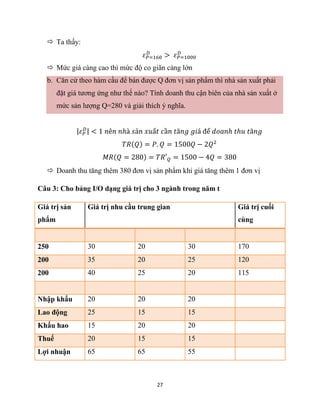
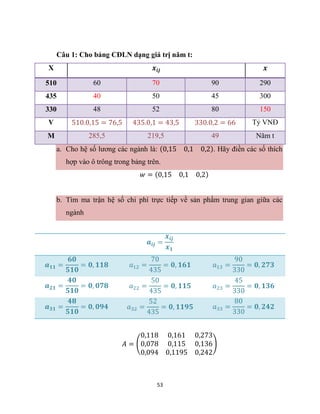
Câu 1: Cho ma trận hệ số chi phí trực tiếp dạng giá trị của 3 ngành năm t:
𝑨 = [
𝟎, 𝟏 𝟎, 𝟒 𝟎, 𝟐
𝟎, 𝟑 𝟎, 𝟐 𝟎, 𝟑
𝟎, 𝟒 𝟎, 𝟏 𝟎, 𝟐
]
𝑪 = (𝑬 − 𝑨)−𝟏
= [
𝟏, 𝟖𝟐 𝟏, 𝟎𝟏 𝟎, 𝟖𝟒
𝟏, 𝟎𝟕 𝟏, 𝟗𝟏 𝟎, 𝟗𝟖
𝟏, 𝟎𝟒 𝟎, 𝟕𝟓 𝟏, 𝟕𝟗
]
Hệ số chi phí lao động: 𝑨𝟎 = (𝟎, 𝟐𝟓 𝟎, 𝟏𝟓 𝟎, 𝟐)
a. Nêu ý nghĩa của 𝑎23, 𝑐23
𝑎23 = 0,3: cho biết ngành 3 muốn sản xuất ra 1 đơn vị giá trị sản phẩm thì
ngành 2 phải cung cấp cho nó 0,3 đơn vị giá trị sản phẩm
𝑐23 = 0,3: cho biết ngành 3 muốn sản xuất ra 1 đơn vị giá trị sản phẩm cuối
cùng thì ngành 2 phải sản xuất cho nó 0,3 đơn vị giá trị sản phẩm
b. Nêu giá trị SPCC các ngành năm t là (420 290 350), tính giá trị TSL
các ngành năm t
𝑞 = (420 290 350)
Gọi TSL các ngành năm t là 𝑄𝑡 = (𝑄1 𝑄2 𝑄3)
𝑄𝑡 = 𝐶𝑡. 𝑞𝑡
= (
1,82 1,01 0,84
1,07 1,91 0,98
1,04 0,75 1,79
) 𝑥 (
420
290
350
) = (
1351,3
1346,3
1230,8
)
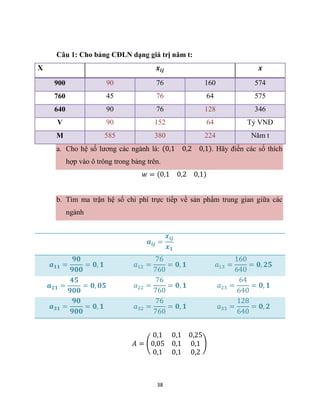
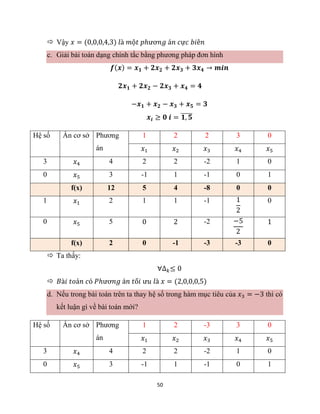
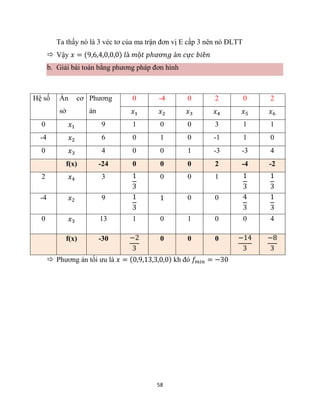
c. Biết rằng mọi hệ số năm t+1 không thay đổi so với năm t. Lập bảng CĐLN
năm t+1 biết giá trị SPCC năm t+1 là (460 335 380)
X 𝒙𝒊𝒋 𝒙
900 90 76 168 460](https://image.slidesharecdn.com/thitonkinhtccnm-220508125302-c96a3169/85/D-THI-TOAN-KINH-T-CAC-NAM-pdf-45-320.jpg)

















![67
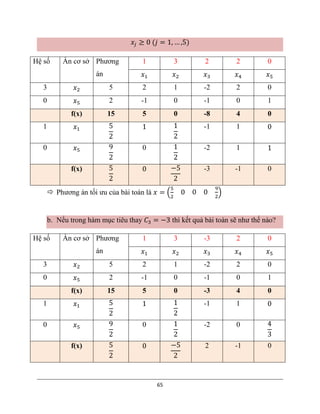
Câu 1: Cho ma trận hệ số chi phí trực tiếp dạng hiện vật của 3 ngành:
𝜶 = [
𝟎, 𝟑 𝟎, 𝟏 𝟎, 𝟒
𝟎, 𝟐 𝟎, 𝟑 𝟎, 𝟏
𝟎, 𝟏 𝟎, 𝟒 𝟎, 𝟐
]
𝜽 = (𝑬 − 𝜶)−𝟏
= [
𝟏, 𝟗 𝟎, 𝟕𝟏 𝟎, 𝟗𝟓
𝟎, 𝟖𝟖 𝟏, 𝟗𝟒 𝟏, 𝟏𝟔
𝟎, 𝟖𝟐 𝟏, 𝟎𝟐 𝟏, 𝟖𝟒
]
Và vector hệ số sử dụng lao động 𝜷 = (𝟎, 𝟑; 𝟎, 𝟐; 𝟎, 𝟐)
a. Nêu ý nghĩa của 𝛼23𝑣à 𝜃23, giải thích sự khác nhau của chúng
𝛼23 = 0,1: cho biết ngành 3 muốn sản xuất ra 1 đơn vị sản phẩm thì ngành 2
phải cung cấp cho nó 0,1 đơn vị sản phẩm
𝜃23 = 1,16: cho biết ngành 3 muốn sản xuất ra 1 đơn vị sản phẩm cuối cùng
thì ngành 2 phải sản xuất cho nó 1,16 đơn vị sản phẩm
b. Biết nhu cầu SPCC của 3 ngành lần lượt là 150, 250, 300 đơn vị. Tính sản
lượng và số lao động phải sử dụng của mỗi ngành
𝑞 = (150 250 300)
𝑄 = 𝜃. 𝑞
= (
1,9 0,71 0,95
0,88 1,94 1,16
0,82 1,02 1,84
) . (
150
250
300
) = (
747,5
965
930
)
𝑆ố 𝑙𝑎𝑜 độ𝑛𝑔 𝑝ℎả𝑖 𝑠ử 𝑑ụ𝑛𝑔 𝑐ủ𝑎 𝑚ỗ𝑖 𝑛𝑔à𝑛ℎ:
𝑄01 = 0,3.747,5 = 224,25
𝑄02 = 0,2.965 = 193
𝑄03 = 0,2.930 = 186
c. Cho tiền công của 3 ngành lần lượt là 15, 25 và 30 đơn vị.
i. Tính giá của sản phẩm](https://image.slidesharecdn.com/thitonkinhtccnm-220508125302-c96a3169/85/D-THI-TOAN-KINH-T-CAC-NAM-pdf-67-320.jpg)






















![91
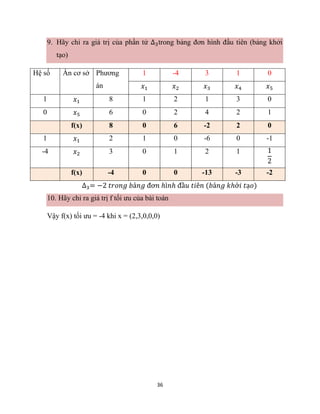
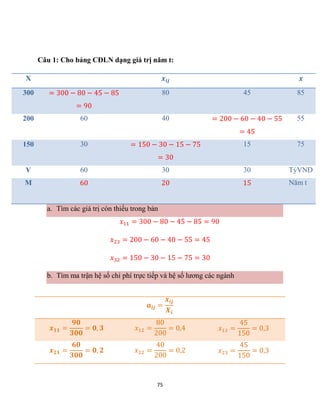
Câu 9: Cho ma trận hệ số chi phí trực tiếp
𝑨 = (
𝟎, 𝟑 𝟎, 𝟒 𝟎, 𝟑
𝟎, 𝟐 𝟎, 𝟐 𝟎, 𝟑
𝟎, 𝟏 𝟎, 𝟏𝟓 𝟎, 𝟏
)
Hệ số lao động: 𝑩 = (𝟎, 𝟐 𝟎, 𝟏𝟓 𝟎, 𝟐)
Lập bảng CĐLN
X xij x
V Tỷ VND
M Năm t
Câu 10: Cho ma trận hệ số chi phí toàn bộ dạng hiện vật:
𝜽 = [
𝟏, 𝟐𝟎𝟕 𝟎, 𝟏𝟔 𝟎, 𝟏𝟐
𝟎, 𝟎𝟗𝟔 𝟏, 𝟐𝟏 𝟎, 𝟏𝟒
𝟎, 𝟐𝟐 𝟎, 𝟐𝟑 𝟏, 𝟏𝟓
]
a. Tìm ma trận hệ số chi phí trực tiếp
𝛼 = 𝐸 − 𝜃−1
= (
1 0 0
0 1 0
0 0 1
) − (
1,207 0,16 0,12
0,096 1,21 0,14
0,22 0,23 1,15
)
−1
= (
0,1497 0,0978 0,0768
0,0497 0,1482 0,0984
0,1527 0,1516 0,096
)](https://image.slidesharecdn.com/thitonkinhtccnm-220508125302-c96a3169/85/D-THI-TOAN-KINH-T-CAC-NAM-pdf-91-320.jpg)