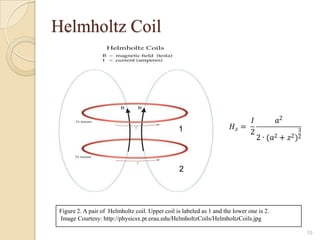
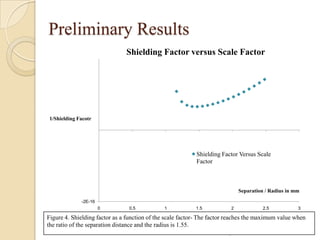
This document discusses finding the optimal setup for shielding external magnetic fields to trap Bose-Einstein condensate (BEC) atoms. It examines using two coils of the same size separated by a varying distance. Preliminary results show shielding factor is maximized when the separation distance between coils is 1.55 times the coil radius based on the Helmholtz configuration. Future work includes analytically evaluating the inverse shielding factor and developing an experiment in spring 2014.

1. Finding the Optimum Setup for
Shielding External Magnetic Field
to Trap the BEC Atoms
Shouvik Bhattacharya
PHY791 | 10.30.2013

2. Problem

We are surrounded by a geomagnetic field.
In addition, there are various factors that
can potentially fluctuate the field
strength, which is undesired for the BEC
study. Some of those factors are: power
source and equipment used in the
laboratory, charged particles (Cosmic
Rays), and the Space Weather.
Bhattacharya
2

3. Thesis

To find the optimum set-up that will
screen fluctuations in external magnetic
field. Two coils of same size are separated
by a varying distance configuration was
mainly focused for this instance.
Bhattacharya
3

4. Theory
Faraday’s law of Induction
 Lenz’s Law
 Properties of superconductor

Bhattacharya
4

5. Faraday’s law of Induction

Bhattacharya
5

6. Lenz’s Law
Figure 1.1 If one passes a bar magnet through the center of the loop, a change in magnetic field
B creates an induced electric field E. Current I loops around counterclockwise, due to
orientation of magnetic pole.
Image Courtesy: http://www.physics.rutgers.edu/ugrad/labs/online/Faraday_html_600e2a63.jpg
Bhattacharya
6

7. Inductance


Self-inductance occurs due to varying
current that passes through the coil.
Mutual-inductance occurs when two
or more coils are connected. Mutualinductance is greater when the
separation between two coils reaches
minimum distance .
Bhattacharya
7

8. Properties of Superconductor
Resistance is zero at the superconducting
transition temperature.
 Superconductor atoms attain the BEC
(Bose-Einstein Condensate) at a very low
temperature.
 Atoms at BEC behave like magnets.

Bhattacharya
8

9. Methods
Review the Helmholtz configuration.
 Talk about the Radia package to evaluate
the field strength for different
configuration.

Bhattacharya
9

10. Helmholtz Coil
1
2
Figure 2. A pair of Helmholtz coil. Upper coil is labeled as 1 and the lower one is 2.
Image Courtesy: http://physicsx.pr.erau.edu/HelmholtzCoils/HelmholtzCoils.jpg
10

11. Radia
Figure 3. Changing the separation parameter and reporting associated
magnetic field with it.
Bhattacharya
11

12. Analyses

Bhattacharya
12

13. Preliminary Results
Shielding Factor versus Scale Factor
1/Shielding Facotr
Shielding Factor Versus Scale
Factor
Separation / Radius in mm
-2E-16
0
0.5
1
1.5
2
2.5
3
Figure 4. Shielding factor as a function of the scale factor- The factor reaches the maximum value when
the ratio of the separation distance and the radius is 1.55.
Bhattacharya
13

14. Future Work
Would like to analyze the function for
finding inverse shielding factor
analytically.
 Will develop a research proposal to do the
experiment in spring 2014.

Bhattacharya
14

15. Acknowledgements

I would like to thank Dr. Jonathan Wrubel
for his continuous help and support to
make progress in this problem.
Bhattacharya
15

16. References
Dyck, R S Van, Moore, Jr. F
L, Farnham, D. L, Schwinberg, P. B.
1986. Rev. Sci Instrun 57 (593).
 Gabrielse G. and Tan. J. 15 May, 1988.
Self-shielding superconducting solenoid
systems. Journal of Applied Physics 10 .
 Grivich Matthew I. Jackson David P. May
2000. The magnetic field of currentcarryingpolygons: An application of
vector field rotations. Ameircan Journal
of Physics 68 (5): 469-74.

Bhattacharya
16

17. Questions
Figure 5. Faraday Medal, front side: Image Courtesy:
http://royalsociety.org/awards/michael-faraday-prize/
Bhattacharya
17