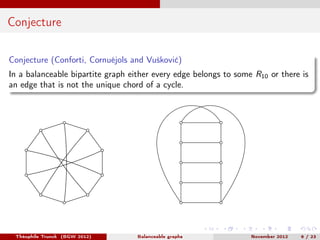
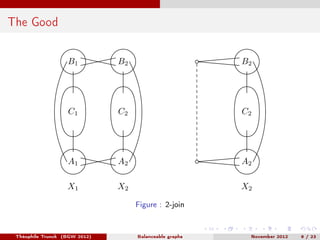
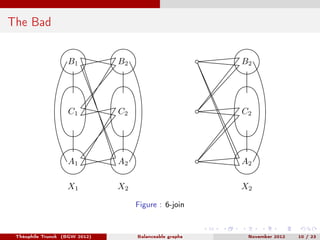
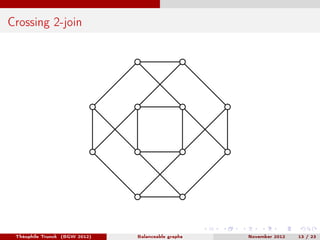
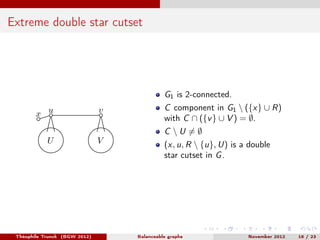
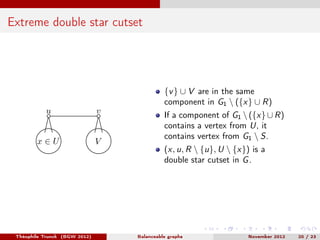
Théophile Trunck presented work on linear balanceable and subcubic balanceable graphs at BGW 2012 in November. The document discusses definitions of balanceable graphs, previous conjectures regarding twins in cubic graphs with induced 4-cycle-free graphs, and results proving the existence of low degree vertices in 4-hole free balanceable graphs. Decomposition theorems are also presented, showing that balanceable graphs can be decomposed using 2-joins, 6-joins, or star cutsets while preserving being balanceable. Open questions are posed regarding building all cubic 4-cycle-free graphs and resolving a previous conjecture.