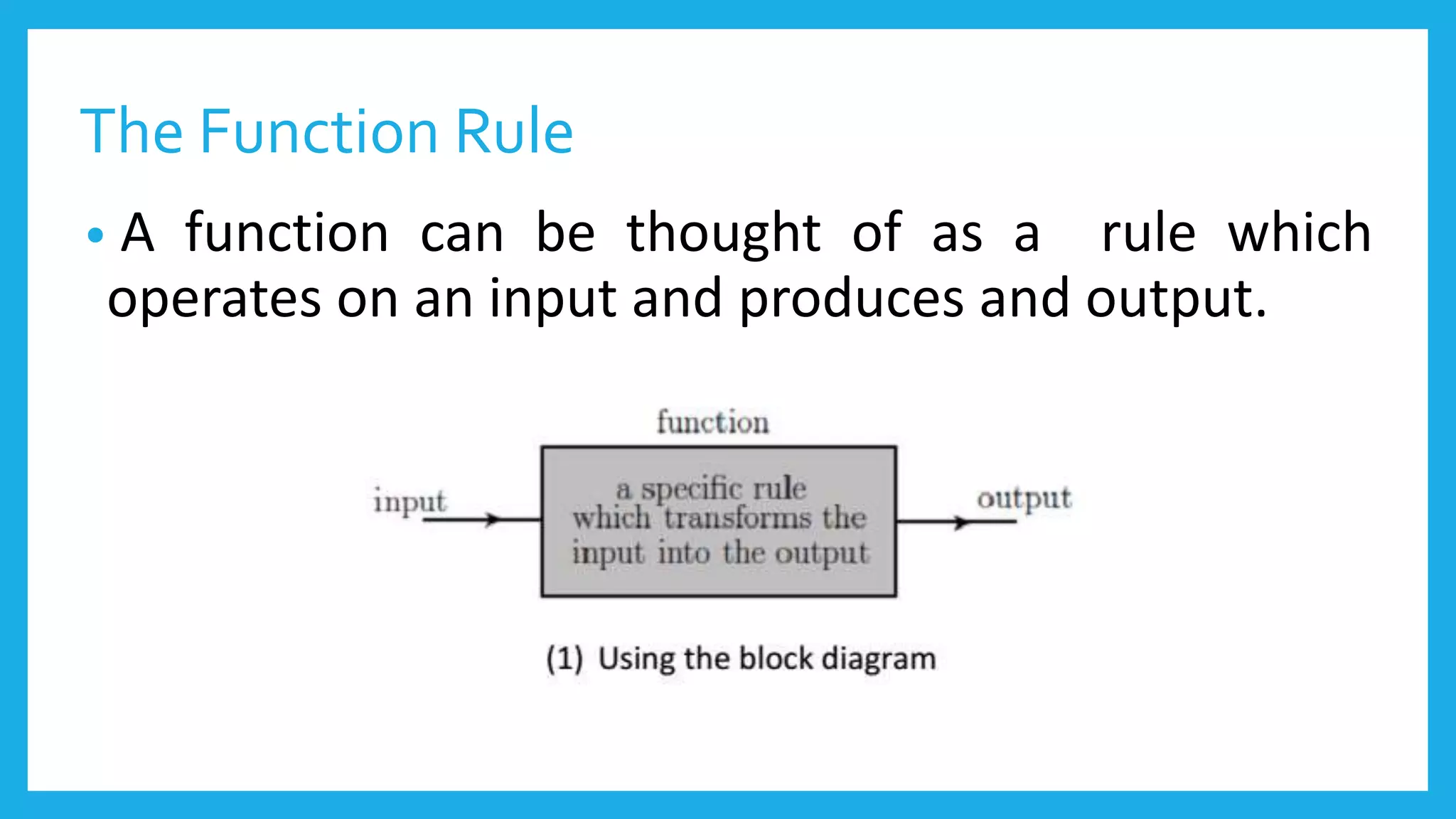
This document introduces functions and function notation. It defines a function as a rule that takes an input and produces an output. It shows examples of functions written in function notation like f(x)=3x and evaluates functions for given inputs. It discusses operations that can be performed on functions like addition, subtraction, multiplication, and composition. It provides examples of evaluating these operations. It also gives real-life examples of functions modeling jeepney fares and investment growth. Finally, it introduces piecewise functions and gives an example of a piecewise function modeling guide fees.

1. FUNCTIONS
INTRODUCTION

2. The Function Rule
• A function can be thought of as a rule which
operates on an input and produces and output.

3. The Function Notation
𝑓 𝑥 = 3𝑥
• Read as “𝒇 as a function of 𝒙” or “𝒇 of 𝒙” or “the rule of 𝒇 is….”
• meaning that the value of the output from the function depends upon the value of the
input x.
• The value of the output is often called the ‘value of the function’.
Name of the
function
Input Output (value of the function)

4. The Function Notation
Given the following functions, find the value of the output with each given
input or argument:
1. Given: 𝑓 𝑥 = 3𝑥 + 1
i. 𝑓 2
ii. 𝑓 −1
iii. 𝑓(6)
2. Given: 𝑦 𝑥 = 3𝑥 + 2
i. 𝑦 𝑡
ii. 𝑦 2𝑡
iii. 𝑦(𝑧 + 2)

5. The Function Notation
Given the following functions, find the value of
the output with each given input or argument:
3. 𝑔 𝑥 = 3𝑥2 − 7
i. 𝑔(3𝑡)
ii. 𝑔 𝑡 + 5

6. Operations on Functions
•Similar to any real numbers, functions can also be added,
subtracted, multiplied and divided.
EQUATION OPERATION
𝒇 + 𝒈 𝒙 = 𝒇 𝒙 + 𝒈(𝒙) Addition
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔(𝑥) Subtraction
𝑓 ∙ 𝑔 𝑥 = 𝑓(𝑥) ∙ 𝑔(𝑥) Multiplication
𝑓
𝑔
𝑥 = 𝑓(𝑥)/𝑔 𝑥 Division
𝑓 ∘ 𝑔 𝑥 = 𝑓(𝑔 𝑥 ) Composition

7. Operations on Functions
Examples:
1. Given 𝑓 𝑥 = 3𝑥 + 2 and 𝑔 𝑥 = 4 − 5𝑥,
Find:
i. (𝑓 + 𝑔)(𝑥)
ii. 𝑓 − 𝑔 𝑥
iii. 𝑓 ∙ 𝑔 𝑥
iv.
𝑓
𝑔
𝑥

8. Operations on Functions
Examples:
2. Given: 𝑓 𝑥 = 2𝑥, 𝑔 𝑥 = 𝑥 + 4, and ℎ 𝑥 = 5 − 𝑥3
.
Find:
i. 𝑓 + 𝑔 2
ii. ℎ − 𝑔 2
iii. 𝑓 ∙ ℎ 2
iv.
ℎ
𝑔
2
v. (𝑔 ∘ ℎ)(2)

9. Drills
For numbers 5 and 6, evaluate the following functions.
5. Given the function 𝑓 𝑥 = 5𝑥 + 8, find the value of the
output given the following input or argument
a. 𝑓 𝑡
b. 𝑓 −8
c. 𝑓 5
d. 𝑓 3𝑥
e. 𝑓(7 − 𝑥)

10. Functions in Real-Life Situations
Example 1:
f(t) = 10,000(1.05)t represent the amount of money if P10,000 is invested at 5% compounded
annually.
Example 2:
Suppose that a jeepney ride costs P8 for the first 4 kilometers, then an additional P1.50 for each
succeeding kilometer.Then the cost of a jeepney fare for a jeepney on an 8-kilometer route can be
modeled by:
𝐹( 𝑑) =
8.00 𝑖𝑓 0 < 𝑑 ≤ 4
9.50 𝑖𝑓 4 < 𝑑 ≤ 5
11.00 𝑖𝑓 5 < 𝑑 ≤ 6
12.50 𝑖𝑓 6 < 𝑑 ≤ 7
14.00 𝑖𝑓 7 < 𝑑 ≤ 8
where d is the distance travelled and F(d) is the fare.

11. Piecewise Function
• Is a function defined by multiple sub-functions with each sub-
function applying to a certain interval of the function’s domain
(or a sub-domain)
𝐹( 𝑑) =
8.00 𝑖𝑓 0 < 𝑑 ≤ 4
9.50 𝑖𝑓 4 < 𝑑 ≤ 5
11.00 𝑖𝑓 5 < 𝑑 ≤ 6
12.50 𝑖𝑓 6 < 𝑑 ≤ 7
14.00 𝑖𝑓 7 < 𝑑 ≤ 8

12. Piecewise Function
Example:
•The fee for hiring a guide to hike Mt. Apo is P700. Suppose that
the guide can take care of at least 8 hikers and a maximum of 16.
For every succeeding 2 hikers, there is an additional fee of P125.
Represent the cost of hiring guides as a piecewise function of the
number of hikers.

13. REVIEWTHE CONCEPTS FOR A SMOOTH
FLOWTHISWEEK! :3