This document outlines the basic limit laws for evaluating limits in functions, including the limit of constant functions, the identity function, and various operation laws such as the sum, product, and quotient laws. It provides examples and explains how to apply these laws to find limits directly without using tables or graphs. Additionally, it mentions a quiz for practicing the application of these limit laws.

1. The Basic
Limit Laws
GRADE 10 – ELECTIVE

2. Illustration of Limit
Laws
The limits laws enable us to directly
evaluate limits, without need for a table
or a graph. Let c is a constant, and f and g
are the function which may or may not
have c in their domains.

3. BASIC LIMIT LAWS
• Limit of a Constant Function
• Limit of an Identity Function
• Constant Multiple Law

4. LIMIT OF A CONSTANT
The limit of a constant is itself. If k is any constant,
then,
lim
𝑥 → 𝐶
𝑘=𝑘

5. LIMIT OF A CONSTANT
The limit of a constant is itself. If k is any constant,
then,
lim
𝑥 → 𝐶
𝑘=𝑘
lim
𝑥 → 5
2=¿

6. LIMIT OF A CONSTANT
The limit of a constant is itself. If k is any constant,
then,
lim
𝑥 → 𝐶
𝑘=𝑘
lim
𝑥 → 5
2=2

7. LIMIT OF A CONSTANT
The limit of a constant is itself. If k is any constant,
then,
lim
𝑥 → 𝐶
𝑘=𝑘
lim
𝑥 → 5
2=2 lim
𝑥 → 1
−1.25=¿

8. LIMIT OF A CONSTANT
The limit of a constant is itself. If k is any constant,
then,
lim
𝑥 → 𝐶
𝑘=𝑘
lim
𝑥 → 5
2=2 lim
𝑥 → 1
−1.25=−1.25

9. LIMIT OF AN IDENTITY FUNCTION
The limit of the identity function f(x) = x approaches c
is equal to c.
lim
𝑥 → 𝐶
𝑥=𝑐

10. LIMIT OF AN IDENTITY FUNCTION
The limit of the identity function f(x) = x approaches c
is equal to c.
lim
𝑥 → 𝐶
𝑥=𝑐
lim
𝑥 → 1.5
𝑥=¿

11. LIMIT OF AN IDENTITY FUNCTION
The limit of the identity function f(x) = x approaches c
is equal to c.
lim
𝑥 → 𝐶
𝑥=𝑐
lim
𝑥 → 1.5
𝑥=1.5

12. LIMIT OF AN IDENTITY FUNCTION
The limit of the identity function f(x) = x approaches c
is equal to c.
lim
𝑥 → 𝐶
𝑥=𝑐
lim
𝑥 → 1.5
𝑥=1.5

13. LIMIT OF AN IDENTITY FUNCTION
The limit of the identity function f(x) = x approaches c
is equal to c.
lim
𝑥 → 𝐶
𝑥=𝑐
lim
𝑥 → 1.5
𝑥=1.5

14. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐦
→𝒄
𝒌 ∙ 𝒇 ( 𝒙 )=¿

15. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐥𝐢𝐦
𝒙 →𝒄
𝒌 ∙ 𝒇 ( 𝒙 )=𝒌∙ 𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )

16. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐥𝐢𝐦
𝒙 →𝒄
𝒌 ∙ 𝒇 (𝒙 )=𝒌∙ 𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )=𝒌∙ 𝑳
𝑥 )

17. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐥𝐢𝐦
𝒙 →𝒄
𝒌 ∙ 𝒇 (𝒙 )=𝒌∙ 𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )=𝒌∙ 𝑳
3 ∙ 𝑓 ( 𝑥 )

18. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐥𝐢𝐦
𝒙 →𝒄
𝒌 ∙ 𝒇 (𝒙 )=𝒌∙ 𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )=𝒌∙ 𝑳
lim
𝑥 → 𝑐
3 ∙ 𝑓 (𝑥)=3 ∙ lim
𝑥→ 𝑐
𝑓 ( 𝑥)=3 (5)=15

19. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐥𝐢𝐦
𝒙 →𝒄
𝒌 ∙ 𝒇 (𝒙 )=𝒌∙ 𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )=𝒌∙ 𝑳
− 2 ∙ 𝑓 ( 𝑥 )= ¿

20. CONSTANT MULTIPLE LAW
The limit of a constant k multiplied by a function is
equal to k multiplied by the limit of the function.
𝐥𝐢𝐦
𝒙 →𝒄
𝒌 ∙ 𝒇 (𝒙 )=𝒌∙ 𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )=𝒌∙ 𝑳
lim
𝑥 → 𝑐
−2 ∙ 𝑓 (𝑥)=−2 ∙ lim
𝑥→ 𝑐
𝑓 ( 𝑥)=−2 (5)=−10

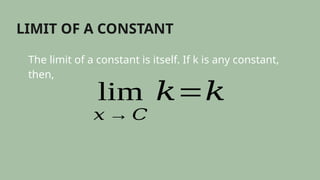
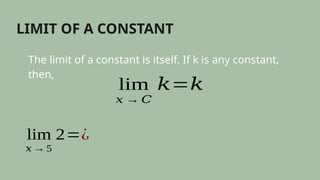
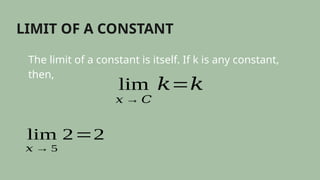
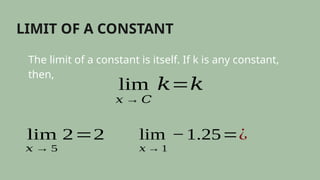
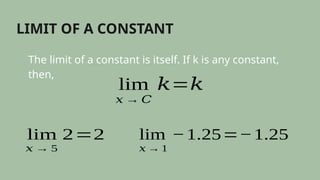
21. SUM OR DIFFERENCE LAW
The limit of the sum or difference of two functions is
equal to the sum or difference of the limits of the two
functions.
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 ( 𝒙 ) ± 𝒈( 𝒙 )]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙) ± 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈( 𝒙 )=𝑳± 𝑴
If and , then
𝐦
𝒄
[ 𝒇 ( 𝒙 )+𝒈 ( 𝒙) ]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙 ) ± 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙)=¿

22. SUM OR DIFFERENCE LAW
The limit of the sum or difference of two functions is
equal to the sum or difference of the limits of the two
functions.
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 ( 𝒙 ) ± 𝒈( 𝒙 )]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙) ± 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈( 𝒙 )=𝑳± 𝑴
If and , then
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 ( 𝒙 )+𝒈( 𝒙) ]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙 ) −𝐥𝐢𝐦
𝒙→ 𝒄
𝒈( 𝒙 )=− 𝟑+𝟒=𝟏

23. SUM OR DIFFERENCE LAW
The limit of the sum or difference of two functions is
equal to the sum or difference of the limits of the two
functions.
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 ( 𝒙 ) ± 𝒈( 𝒙 )]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙) ± 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈( 𝒙 )=𝑳± 𝑴
If and , then
𝐢𝐦
→𝒄
[ 𝒇 ( 𝒙 ) −𝒈 ( 𝒙)]=𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )− 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙 )=¿

24. SUM OR DIFFERENCE LAW
The limit of the sum or difference of two functions is
equal to the sum or difference of the limits of the two
functions.
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 ( 𝒙 ) ± 𝒈( 𝒙 )]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙) ± 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈( 𝒙 )=𝑳± 𝑴
If and , then
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 ( 𝒙 ) −𝒈 ( 𝒙)]=𝐥𝐢𝐦
𝒙 →𝒄
𝒇 ( 𝒙 )− 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈( 𝒙 )=−𝟑− 𝟒=−𝟕

25. PRODUCT LAW
The limit of the product of two functions is equal to the
product of the limits of the two functions.
If and , then
𝒇 ( 𝒙 ) ∙ 𝒈 ( 𝒙 )]=𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 (𝒙 ) ∙ 𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙)=¿

26. PRODUCT LAW
The limit of the product of two functions is equal to the
product of the limits of the two functions.
If and , then
𝐥𝐢𝐦
𝒙 →𝒄
[ 𝒇 (𝒙 )∙𝒈(𝒙 )]=𝐥𝐢𝐦
𝒙→ 𝒄
𝒇 (𝒙 ) ∙𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙)=𝟔(−𝟖)=−𝟒𝟖

27. QUOTIENT LAW
The limit of the quotient of two function is equal to the
quotient of the limits of the two functions, provided
that the limit of the divisor is not equal to zero.
𝐥𝐢𝐦
𝒙 →𝒄
𝒇 (𝒙 )
𝒈(𝒙 )
=
𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙)
𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙)
=
𝑳
𝑴
provided that 𝑀

28. QUOTIENT LAW
𝐥𝐢𝐦
𝒙 →𝒄
𝒇 (𝒙 )
𝒈(𝒙 )
=
𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙)
𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙)
=
𝑳
𝑴
provided that 𝑀
For example, if and ,

29. QUOTIENT LAW
𝐥𝐢𝐦
𝒙 →𝒄
𝒇 (𝒙 )
𝒈(𝒙 )
=
𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 ( 𝒙)
𝐥𝐢𝐦
𝒙 → 𝒄
𝒈 ( 𝒙)
=
𝑳
𝑴
provided that 𝑀
For example, if and ,

30. POWER LAW
The limit of the integral power of a function is equal to
the integral power of the limit of the function,
provided that the limit of the function is not equal to
zero when the exponent is negative, i.e. when .
𝐥𝐢𝐦
𝒙 →𝒄
[𝒇 (𝒙 )]
𝒏
=
[𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 (𝒙 )
]
𝒏
=𝑳𝒏
provided that when

31. POWER LAW
𝐥𝐢𝐦
𝒙 →𝒄
[𝒇 (𝒙 )]
𝒏
=
[𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 (𝒙 )
]
𝒏
= 𝑳
𝒏
provided that when
For example, if ,

32. POWER LAW
𝐥𝐢𝐦
𝒙 →𝒄
[𝒇 (𝒙 )]
𝒏
=
[𝐥𝐢𝐦
𝒙 → 𝒄
𝒇 (𝒙 )
]
𝒏
= 𝑳
𝒏
provided that when
For example, if ,

33. ROOT LAW
The limit of the th
root of a function is equal to the th
root
of the limit of the function, where is a positive integer,
and the limit of the function is positive when is even. In
symbols:

34. ROOT LAW
For example, if , then

35. ROOT LAW
For example, if , then

36. QUIZ
TOMORROW!
10-09-24

37. Direction: Evaluate and identify the limits using the Limit
Laws. Show each steps.
QUIZ 1
lim
𝑥 → 5
2=2− 𝐿𝑖𝑚𝑖𝑡 𝑜𝑓 𝑎𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
Ex.
1. lim
𝑥 → 5
(2 𝑥 − 3 𝑥+ 4)
2
2.
lim
𝑥 → 9
8 𝑥
3. If and
=
4. lim
𝑥 → 7.6
𝑥=¿
5.
𝐥𝐢𝐦
𝒙 →𝒄
𝟐 ∙ 𝒇 ( 𝒙 )=¿
c = 3