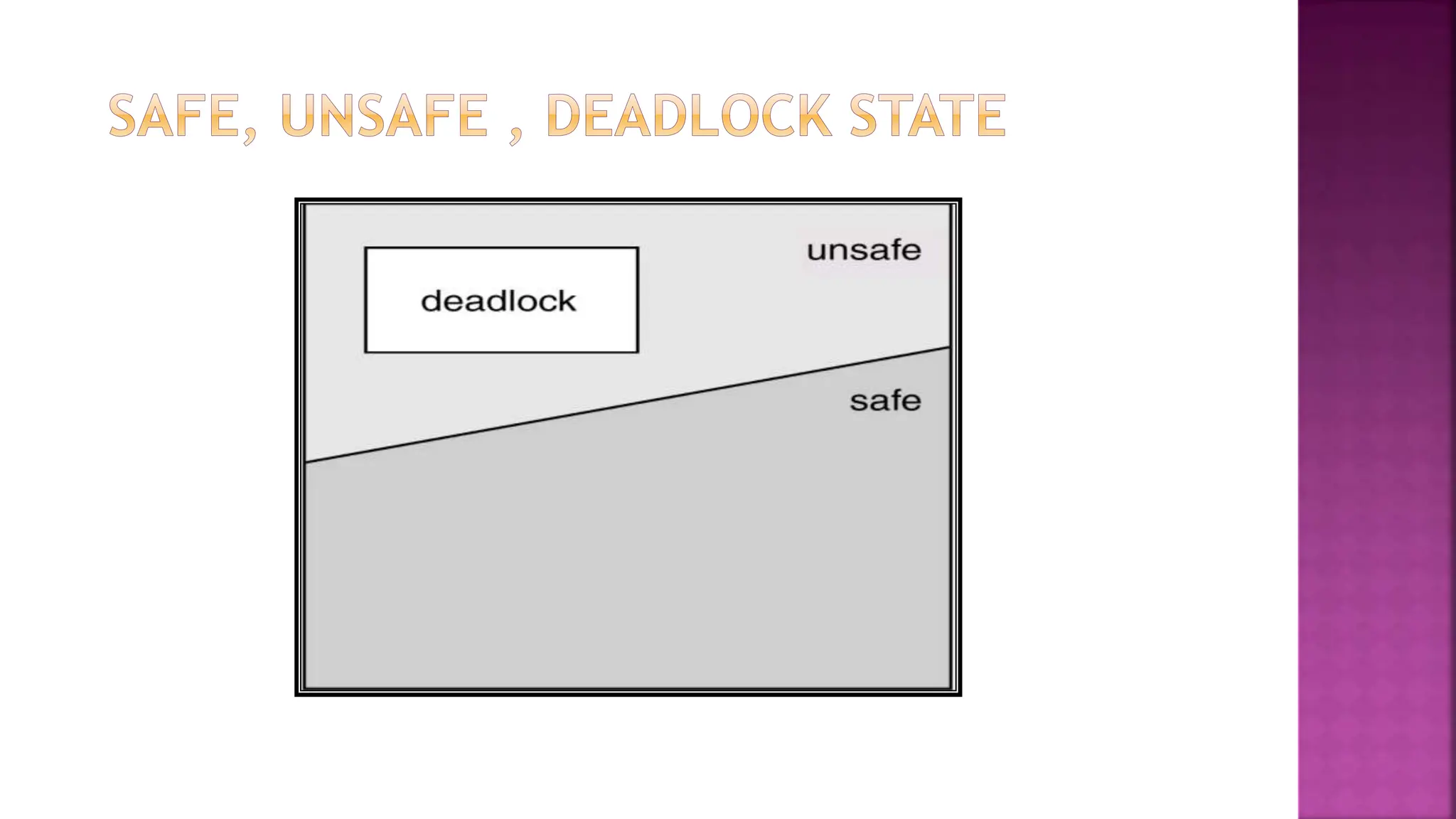
The document discusses a model for resource allocation and deadlock avoidance, emphasizing the importance of knowing the maximum resource needs of each process. It details the Banker’s algorithm, which checks if resource allocation can proceed without entering an unsafe state, and outlines the steps for simulating resource allocation. The overall goal is to ensure that the system remains in a safe state to prevent deadlock situations.

2.  Simplest and most useful model requires that each
process declare the maximum number of resources of
each type that it may need.
 Resource-allocation state is defined by the number of
available and allocated resources, and the maximum
demands of the processes.
 The deadlock-avoidance algorithm dynamically
examines the resource-allocation state to ensure that
there can never be a circular-wait condition.
Requires that the system has some additional a priori information
available.

3.  When a process requests an available resource, system must decide if
immediate allocation leaves the system in a safe state.
 System is in safe state if there exists a safe sequence of all
processes.
 Sequence <P1, P2, …, Pn> is safe if for each Pi, the resources that Pi
can still request can be satisfied by currently available resources +
resources held by all the Pj, with j<I.
 If Pi resource needs are not immediately available, then Pi can wait until all
Pj have finished.
 When Pj is finished, Pi can obtain needed resources, execute, return
allocated resources, and terminate.
 When Pi terminates, Pi+1 can obtain its needed resources, and so on.

4.  If a system is in safe state  no deadlocks.
 If a system is in unsafe state  possibility of deadlock.
 Avoidance  ensure that a system will never enter an unsafe
state.

6.  The banker’s algorithm is a resource allocation and deadlock
avoidance algorithm
 In this each process’s maximum recourses need must be
known in advance
 It tests for safe state by simulating the allocation for
predetermined maximum possible amounts of all resources,
before deciding whether allocation should be allowed to
continue.

7.  Let ‘n’ be the number of processes in the system and ‘m’ be the
number of resources types.
Available:
It is a 1-d array of size ‘m’ indicating the number of available
resources of each type.
 Available[ j ] = k means there are ‘k’ instances of resource type Rj

8. Max:
It is a 2-d array of size ‘n*m’ that defines the maximum demand of each
process in a system.
 Max[ i, j ] = k means process Pi may request at most ‘k’ instances of
resource type Rj.

9. Allocation :
It is a 2-d array of size ‘n*m’ that defines the number of resources of each type
currently allocated to each process.
Allocation[i,j] = k means process Pi is currently allocated ‘k’ instances of resource
type Rj

10. Need :
It is a 2-d array of size ‘n*m’ that indicates the remaining resource need of each process.
Need [ i,j] = k means process Pi currently need ‘k’ instances of resource type Rj for its
execution.
Need [ i,j] = Max [i,j] – Allocation [i,j]
Allocationi specifies the resources currently allocated to process Pi and Needi specifies the
additional resources that process Pi may still request to complete its task.

11. 1) Let Work and Finish be vectors of length ‘m’ and ‘n’ respectively.
Initialize: Work = Available
Finish[i] = false; for i=1, 2, 3, 4….n
2) Find an i such that both
a) Finish[i] = false
b) Needi <= Work
if no such i exists goto step (4)
3) Work = Work + Allocation[i]
Finish[i] = true
goto step (2)
4) if Finish [i] = true for all i
then the system is in a safe state

12. Let Requesti be the request array for process Pi. Requesti [j] = k means process Pi wants k
instances of resource type Rj. When a request for resources is made by process Pi, the
following actions are taken:
1) If Requesti <= Needi
Goto step (2) ; otherwise, raise an error condition, since the process has exceeded its
maximum claim.
2) If Requesti <= Available
Goto step (3); otherwise, Pi must wait, since the resources are not available.
3) Have the system pretend to have allocated the requested resources to process Pi by
modifying the state as
follows:
Available = Available – Requesti
Allocationi = Allocationi + Requesti
Needi = Needi– Requesti

13. 2 0

14. - =
Calculating Need
Max [i, j] – Allocation [i, j] = Need [i, j]
0 0
3 2