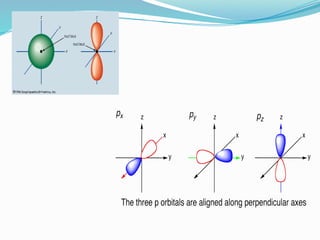
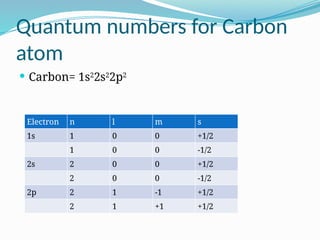
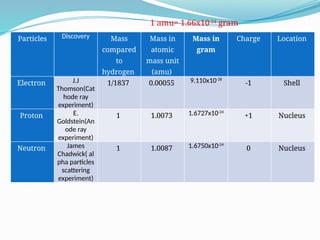
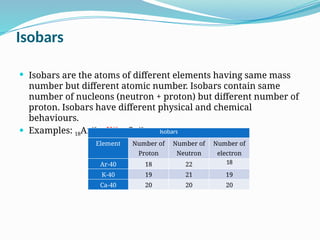
The document covers atomic structure, detailing the composition of atoms, including protons, neutrons, and electrons, and explaining key concepts like atomic number, mass number, isotopes, isobars, and isotones. It also discusses historical atomic models, specifically Thomson's plum pudding model, Rutherford's nuclear model, and Bohr's atomic theory, highlighting their postulates and limitations. Additionally, the document addresses the quantum mechanical model of the atom, including de Broglie's equation and the Heisenberg uncertainty principle.

1. Atomic Structure
Rajesh Poudel

2.  The smallest particle of an element that can take
part in chemical reaction is called atom.
 Atom consists of three subatomic particles-
proton, electron and neutron(fundamental
Particles).
Atom and its fundamental particles

3. Particles Discovery Mass
compared
to
hydrogen
Mass in
atomic
mass unit
(amu)
Mass in
gram
Charge Location
Electron J.J
Thomson(Cat
hode ray
experiment)
1/1837 0.00055 9.110x10-28
-1 Shell
Proton E.
Goldstein(An
ode ray
experiment)
1 1.0073 1.6727x10-24
+1 Nucleus
Neutron James
Chadwick( al
pha particles
scattering
experiment)
1 1.0087 1.6750x10-24
0 Nucleus
1 amu= 1.66x10-24
gram

4.  The number of protons an atom contains is
known as its atomic number. e.g, A helium atom
contain two proton and therefore has atomic
number 2. The identity of an element is
determined by the number of protons in its
atoms-its atomic number.
 Atomic Number =No. of proton
Atomic Number (Z)

5.  The sum of the number of protons and the
number of neutrons gives the mass number of
the element.
 Mass Number= number of protons + number of
neutron.
Mass Number (A)
Mass number is different from
atomic mass or atomic weight

7.  The symbol represent potassium atom.
 Its atomic number is 19.
 Its mass number is 40.
 Number of proton= 19
 Number of electron= 19
 Number of neutron= 40-19= 21
What information can you obtain from the
symbol 19K40
or K-40 ?

8.  What information do you obtain from:
1H2
11Na23
8O16
17Cl35
17Cl-
8O2-
19K+
Do yourself:

9. Isotopes, isobars and isotones

10.  Isotopes are atoms with the same number of
protons, but a different number of neutrons ( or
with same atomic number but different mass
number).
 Example: C-12 (6C12
), C-13(6C13
), C-14(6C14
)
Isotopes of an element
Naturally occurring isotopes of Carbon, C
Atomic
Number
Number
of Proton
Number
of
Neutron
Mass
Number
C-12 6 6 6 12
C-13 6 6 7 13
C-14 6 6 8 14

11.  Isobars are the atoms of different elements having same mass
number but different atomic number. Isobars contain same
number of nucleons (neutron + proton) but different number of
proton. Isobars have different physical and chemical
behaviours.
 Examples: 18Ar40
,19K40
,20Ca40
Isobars
Isobars
Element Number of
Proton
Number of
Neutron
Number of
electron
Ar-40 18 22 18
K-40 19 21 19
Ca-40 20 20 20

12.  Isotones are the atoms of different elements
having same number of neutrons but different
atomic number (proton).
 Examples: 6C14
, 7N15
and 8O16
are isotones of each
other containing 8 neutrons in each.
Isotones:
Isotones
Element Number of
Proton
Number of
Electron
Number of
neutron
C-14 6 6 8
N-15 7 7 8
O-16 8 8 8

13. Isotones
Element Number of
Proton
Number of
Electron
Number of
neutron
C 6 6 8
N 7 7 8
O 8 8 8
Isobars
Element Number of
Proton
Number of
Neutron
Number of
electron
Ar 18 22 18
K 19 21 19
K 20 20 20
Naturally occurring isotopes of Carbon, C
Atomic Number Number of
Proton
Number of
Neutron
Mass Number
6 6 6 12
6 6 7 13
6 6 8 14

14. Thomson’s model of atom
 J.J. Thomson's experiments
with cathode ray tubes
showed that all atoms
contain tiny negatively
charged subatomic
particles or electrons.
Thomson proposed
the plum pudding
model of the atom, which
had negatively-charged
electrons embedded
within a positively-charged
"soup."

15. RUTHERFORD’S MODEL OF ATOM (RUTHERFORD'S α-RAY
SCATTERING EXPERIMENT):
Rutherford's model of atom is based on the alpha ray
scattering experiment which was performed by Earnest
Rutherford and his coworkers in the year 1910. In α-ray
scattering experiment, particles emitted from a radioactive
substance were bombarded on a thin gold foil, and the fate
of these particles was detected by placing a movable screen
coated with zinc sulphide around the gold foil.

16. Observations:
1. Most of the α-particles (nearly 99%) passed through the
gold foil without deflection.
2. Some of α- particles deflected through small angles.
3. Very few (about 1 in 1,00,000) α particles were deflected
through angles more than 90% of even bounced back.

17. Inferences/Conclusion:
Alpha particles are positively charged helium ion which gets deflected away from other positively charged mass.
1. Since most of the α-particles passed through the gold foil without
deflection, it means that there is a large empty space within the atom.
In other words, atom is mostly empty.
2. Since some of the α-particles are deflected through small angles, it
means that there is a heavy positively charged mass present in the
atom. Moreover this mass must be occupying a very small space within
the atom. In other words atom contains positively charged mass
occupying extremely small volume.
3. The strong deflection or even bouncing back of α- particles from the
gold foil must be due to the close encounter of α- particles with the
massive positively charged mass present in the atom.

19. Important postulates of Rutherford’s
nuclear model of atom
1. Atom consists of a positively charged nucleus around
which negatively charged electrons revolve.
2. Most of the space between the nucleus and the
revolving electron is empty.
3. Nucleus occupy a very small space within the atom. Its
size is extremely small compared to the size of the atom.
4. The entire mass of atom is concentrated at the nucleus.
5. The centrifugal force of the revolving electron is
balanced by the electrostatic force of attraction
between the electron and the nucleus.

20. Defects of Rutherford's model of atom
1. Inability to explain the stability of atom: Rutherford model of
atom could not explain why the electrons which lose energy
continuously do not fall into the nucleus collapsing the atom.
2. Inability to explain the formation of atomic spectra:
Rutherford's model of atom could not explain the origin of
line spectra of atoms.

21. Solved Questions:
 What are alpha particles?
 Why did Rutherford select gold for his alpha
particle scattering experiment?
 What is the use of zinc sulphide screen in alpha
ray scattering experiment?

22. Do yourself:
1. What are the conclusions made by Rutherford's alpha ray
scattering experiment about the structure of atom? What is
the major drawback of this model? Explain.
2. What are the postulates of nuclear model of atomic structure
according to Rutherford's alpha particle scattering
experiment? Pont out its limitation.
3. What experimental evidences led Rutherford to conclude that:
a. The nucleus of the atom contains most of the atomic mass
b. The nucleus of the atom is positively charged
c. The atom consists of mostly empty space.

23. BOHR’S MODEL OF ATOM/Bohr’s atomic theory
1. Electron in an atom revolves round the nucleus in a
certain selected orbit which possesses a definite
amount of energy. Hence, these orbits are called
stationary states.
2. So long as the electron is in any particular stationary
state it will not radiate energy despite the demand of
classical electrodynamics.
3. Only those orbits are possible for which angular
momentum of the electron is integral multiple of
h/2π where h is Planck’s constant. (Quantization of
angular momentum)
Mathematically
mvr = nh/2 π
where,
n= principal quantum number
m= mass of electron
v= linear velocity of the electron
r= radius of the orbit
mvr= angular momentum of the electron
h= Planck’s constant= 6.62x10-27
erg x sec
4. When energy is supplied to an atom, electron can jump
from one orbit(energy level) to another. In doing so they
radiate or absorb a definite amount of energy. The amount
of energy absorbed or emitted is equal to the difference in
energy between the two energy level. The difference in
energy is given out as a single quantum in the form of
radiation and is given by
ΔE = E2 –E1 = hν
Where,
E2= energy of the electron in the higher state n=2
E1= energy of the electron in the lower state n=2
ν= frequency of radiation emitted,
h=Plank’s constant
5. Origin of atomic spectra: When electron jumps from
higher energy level to lower energy level, energy is released
and a emission spectrum is produced . Similarly when
electron jumps from lower to higher energy level, energy is
absorbed and an absorption spectra is produced.

26. Conclusion/Summary
Atom consists of positively charged nucleus around which
negatively charged electrons revolve in selected non radiating
orbits known as stationary states. The centrifugal force of
revolving electron is balanced by the columbic force of
attraction. In a stationary state, the angular momentum of the
electron is equal to the integral multiple of h/2 π and electrons
can jump from one stationary state to another. In doing so the
difference in energies between the two stationary states is
emitted or absorbed in the form of electromagnetic radiation
which gives rise to atomic spectra.

27. Do yourself:
4. Write down the main postulates of Bohr’s atomic model.
How does the model correct the defect of Rutherford's
atomic model?

28. Interpretation of hydrogen spectra on the basis of Bohr’s theory:
The origin of the Hydrogen spectra can be explained on the basis of Bohr's
Theory.
When electric discharge is passed through hydrogen gas at low pressure,
first of all hydrogen molecules are split into atoms, then hydrogen atoms
absorbs more energy whereby electrons are promoted to higher energy
levels. The electrons in higher energy states are unstable hence the electrons
jumps to lower energy states emitting electromagnetic radiation which gives
rise to line spectra (hydrogen spectra).
The wave length of different lines in the spectra can be calculated from the
following empirical equation.
1/λ = R(1/n1
2
- 1/n2
2
) where R= Rydberg’s constant= 109677 cm-1

30. Spectral series in hydrogen atom
Series n1 n2 Spectral Region Wave length
(A0
)
Lyman 1 2,3,4… Ultraviolet 920- 1200
Balmer 2 3,4,5… Visible 4000- 6500
Paschen 3 4,5,6… Infrared 9500-18750
Brackett 4 5,6,7… Infrared 19450-
40500
Pfund 5 6,7,8… Far infrared >40500

31. The following spectral line is obtained is
hydrogen spectra.
 Lyman series: Lyman series is obtained when electron
jump from any of the higher energy level(n2=2,3,4,5….)
to first energy level (n1= 1). This series is obtained in
UV region(920 to 1200 A0
). The wave length of the
spectral line in Lyman series is given by:
 1/λ = R(1/12
- 1/n2
2
) where, n2= 2,3,4,5…..
 Balmer series:
 Paschen series:
 Brackett series:
 Pfund series:

32. Advantages of Bohr’s atomic model
 Stability of atom: Electron in an atom revolves round the nucleus
in a certain selected orbit known as stationary state or orbit which
possesses a definite amount of energy. So long as the electron is in
any particular stationary state it will not radiate energy despite the
demand of classical electrodynamics. The angular momentum of
electron is also quantized. The centrifugal force of revolving electron
is balanced by the columbic force of attraction. Therefore, atom is
stable and it do not jump into the nucleus.
 Formation of hydrogen spectra: This model explains that the
formation of hydrogen spectra occurs when energy is releases during
the transition of electron from higher energy level to lower energy
level.

33. Limitations of Bohr's atomic model:
a) It is only applicable for single electron system like H, He+
, Li++
,
Be+++
etc
b) It does not explain about the splitting of spectral lines during
high resolution i.e, about "fine structure".
c) This theory is not accordance with Heisenberg Uncertainty
Principle.
d) It does not explain dual nature of electron.
e) It does not explain about splitting of spectral lines in
magnetic field(Zeeman’s effect) and in electric field(Stark’s
effect).

34. Solved Questions:
1. Why does hydrogen gas show large number of line spectra (discontinuous) though H-atom
contains one electron?
When hydrogen atom gains energy, its electron can get promoted to any of the higher energy level
(n2=2, 3, 4, 5….) according to the quantum of radiation absorbed. In the same way, when electron
emits radiation, it can return to any of the lower energy level (n1= 2, 3, 4, …..) and emission
spectrum is observed. So there are several but limited number of energy levels between which
transitions can occur. So, hydrogen gas shows large number of discontinuous line spectra.
2. Why is it that electrons do not jump into the nucleus?
Or, How does Bohr’s atomic theory explain the stability of atom?
Electron in an atom revolves round the nucleus in a certain selected orbit known as stationary state
or orbit which possesses a definite amount of energy. So long as the electron is in any particular
stationary state it will not radiate energy despite the demand of classical electrodynamics. The
angular momentum of electron is also quantized. The centrifugal force of revolving electron is
balanced by the columbic force of attraction. Therefore, atom is stable and it do not jump into the
nucleus.

35. Do yourself:
5. What is continuous and discontinuous spectrum? Give example.
6. Name the spectral series which appears visible part of the electromagnetic
spectrum. How is such series originated?
7. How is Balmer series and Paschen series originated in hydrogen spectra?
8. What is quantization of angular momentum?
9. Why is it that electrons do not jump into the nucleus?
10. What is meant by atomic spectrum?
11. Mention any two limitations of Bohr's theory.
12. How does Bohr’s theory predict the origin of line spectra of hydrogen atom?
13. Explain hydrogen spectra in the light of Bohr’s theory. Why does hydrogen
gas show large number of line spectra though hydrogen atom contains one
electron?

36. Solved questions:
 The spectrum of frequencies of electromagnetic radiation
emitted or absorbed during transitions of electrons
between energy levels within an atom. Each element has
a characteristic spectrum by which it can be recognized.
 A continuous spectrum contains many different colors,
or wavelengths, with no gaps. Perfectly white light shined
through a prism causes dispersion of the light, and we see
a rainbow. This is a continuous spectrum.
 A discontinuous electromagnetic spectrum is
a spectrum that contains gaps, holes, or breaks in terms
of the wavelengths that it contains. Example: Hydrogen
spectra

37. Solved Questions:
1. Why is that electrons does not jump into the nucleus?
 According to Bohr's model, atom consists of positively charged
nucleus around which negatively charged electrons revolve in
selected non-radiating orbits known as stationary states. The
electron revolving in the stationary states has a fixed amount of
energy. Morever, the least possible orbit for an atom is the first
shell or energy level with principal quantum number,n=1. The
electron does not jump into the nucleus because the centrifugal
force of revolving electron is balanced by the columbic force of
attraction. However, electron can jump from one orbit to another
when it absorbs or emits quantum of radiation.

38. Wave mechanical model/Quantum
mechanical model
1. De-Broglie’s equation
2. Heisenberg’s Uncertainty Principle
3. Probability concept (Orbital concept)

39. DE-BROGLIE EQUATION
—The quantum mechanical model of atom is based on the wave-particle duality
of matter.
 —In 1924, a French physicist, de Broglie, suggested that the matter or particles
in motion show the dual nature of particle and wave. For example, in
electron microscope, electron behaves as a wave like light wave.
 —This idea of wave particle duality of matter led him to derive the following equation
which includes the behavior of matter in motion both as a particle and as wave.
λ=h/mv
Where λ= wavelength of the moving particle
h= Planck's constant
m= mass of electron
v= velocity of electron
For an object with negligible mass (like electron), the wave character
is significant and particle character is insignificant.
Similarly, for an object with large mass (like a cricket ball) the
particle character is significant and wave character is insignificant.

40. Derivation of de Broglie’s equation
 From Einstein equation;
 E= mc2
…..(i)
where, m= mass of photon and c= velocity of light
 From Planck’s equation;
 E= hν …..(i)
 where, h=planck’s constant and v= frequency of radiation
 From equation 9i) and (ii)
 mc2
= hν
 mc2
= h(c/ ) [ν= c/ ]
 = h/mc (for light)
 = h/mv (for any material particle)
 The equation is de-Broglie’s equation.
 Therefore,
 α(1/p) where mv= p= momentum
 It follows that wave length of a particle is inversely proportional to its momentum.

41. Do yourself:
14.What is de Broglie equation?
15.What is wave particle duality? Write an equation to
show wave particle duality of electron.
16.What is matter wave? How is the wave length of matter
wave determined?

42. HEISENBERG UNCERTANTY PRINCIPLE
Heisenberg Uncertainty principle states that, 'It is impossible to determine simultaneously
the position and momentum of microscopic particles with absolute certainty".
Mathematically,
 Where, ∆x and ∆p are uncertainty in position and momentum respectively and h is
planck's constant.
It means that,
1. If we measure the position more accurately, then uncertainty in momentum becomes
large.
2. If we measure the momentum accurately, the uncertainty in position becomes large.
Bohr's model of atom violates uncertainty principle for it describes simultaneously both
location and momentum of the planetary electron.

43. Do yourself:
17. Which principle goes against the concept of Bohr's
fixed orbits? State the principle.

44. Solved Questions:
1. Why is Bohr's model appeared to be defective in the light of Heisenberg's
Uncertainty principle?
 According to Bohr's model, atom consists of positively charged nucleus around which
negatively charged electron revolve in selected non-radiating orbits known as
stationary states. In stationary state, the angular momentum of the electron
quantized and is equal to the integral multiple of nh/2π.
 However, according to Heisenberg uncertainty principle, it is impossible to
determine simultaneously the exact position and momentum of electron with
absolute certainty. It means in an atom, electron does not always remains at a fixed
distance from the nucleus. It keeps moving in the whole space around the nucleus,
but tends to remain most of the time within a small volume around the nucleus,
where the probability of locating the electron is maximum.
 Thus, Bohr's idea of definite orbit appeared defective in the light of Heisenberg's
uncertainty Principle.

45. ATOMIC ORBITALS
The region around the nucleus where the probability of finding electron is maximum is
called orbital.
Types of orbital:
1. s-orbital
2. p-orbital
3. d-orbital
4. f- orbital
Shape of s-orbitals: s-orbitals are spherical in shape. The size of the s-orbital increases
with increase in the principle quantum number, n. s- orbital is non- directional in nature.
For s- orbital l= 0 and m=0.therefore there is only one s- orbital.
Shape of p-orbitals: p-orbital has dumb-bell shape. For p-orbital l= 1 and therefore m can
have three values +1, 0 -1, therefore there are three p orbital oriented at x, y and z- axes
i.e. px, py and pz. P- orbital are thus directional in nature.

47. Do yourself:
18.What is an atomic orbital? How is it different from
orbit?
19.Write the shape of s and p orbital.

48. Differences between orbit and orbital
Orbit Orbital
1. It is the well defined circular path
around the nucleus where electron
revolves.
2. All orbits are circular.
3. It represents the
planar(2dimensional) motion of an
electron around the nucleus.
4. Orbits do not have directional
character.
5. The concept of orbit is not in
accordance with Heisenberg’s
Uncertainty principle.
6. The maximum number of electron
in an orbit is given by 2n2
where n
is principal quantum number.
1. It is the space around the nucleus
where the probability of finding the
electron is maximum.
2. Different orbitals have different
shapes.
3. It represent the three dimensional
motion of an electron around the
nucleus.
4. All orbitals except s-orbital have
directional character.
5. The concept of orbitals is in
accordance with Heisenberg’s
Uncertainty principle.
6. An orbital can have maximum of 2
electrons.

49. QUANTUM NUMBERS:
Quantum numbers are those numbers which are
used to characterize the state of an electron in an
atom. Electrons in an atom are completely
described by the set of four quantum numbers.
The four quantum numbers are;

50. Principal quantum number (n):
It is introduced by Neil Bohr. It represents the main shell or energy level
around the nucleus. It specifies the location and energy of electron in an atom.
It is denoted by 'n' and its values are 1, 2, 3, 4 … or denoted by K, L, M, N ……
E .It permits the electrons in different shells according to 2n2
rule. Thus the
first, second, third, fourth and fifth shell can accommodate 2, 8, 18, 32 and 50
electrons respectively.
Significance of principal quantum number:
1. It gives an average distance of the electron form the nucleus.
2. It determines the energy of an electron of nth shell.
3. It gives maximum numbers of electrons present in any shell by 2n2
.
4. It explains the main lines of a spectrum.

51. Azimuthal quantum number (l):
It is introduced by Somerfield to explain the fine lines observed with high power
spectroscope. It represents the sub-shell of the main shell. It describes the shape of
the sub-shell (orbital) in which the electron is located. It is also called subsidiary
quantum number. The sub-shells are designated by s, p, d and f. It is denoted by 'l'. Its
value depend on the principle quantum number and ranges from 0 to (n-1).
For n= 1 (K shell), l-=0 (only one subshell)
For n=2 (L shell) l= 0,1 (two subshells)
For n=3 (M shell), l= 0,1,2 (three subshells)
For n=4 (N shell), l=0,1,2,3 (four subshells)
Subshells with n= 0,1,2,3 are designated as s,p,d and f orbitals respectively. It permits
electrons in different orbital according to 2(2l+1) rule. Thus first shell has only one sub-
shell, second shell has two sub-shells, and third shell has three sub-shells and so on.

52. Significance of azimuthal quantum number:
1.It explains the fine lines observed in the spectrum with high
power spectroscope.​
2.It determines the number of subshell in the main shell.​
3.It gives information about the angular momentum of the
electron present in any subshell.​
4.It gives relative energies of various subshells which follows the
order s< p< d< f.​
5.It gives the shape of the subshells.​
6.It helps to determine the total number of electrons that can be
accommodated in a given subshell which is equal to 2(2l+1).​

53. Magnetic quantum number (m):

It was introduced by Linde to explain Zeeman effect. It represents the orientation of the orbitals in
space in presence of magnetic field. It is denoted by 'm' .Its values depend on the azimuthal
quantum number and ranges from +l to –l including 0.

When l=0 (s-subshell), m=0 (only one orbital)

When l=1 (p-subshell), m=+1, 0, -1 (three orbital)

When l=2 (d-subshell), m=+2, +1, 0, -1, -2 (five orbital)

When l=3 (f-subshell), m=+3, =2, =1, 0, -1, -2, -3 ( seven orbital)

For every 'l' values of azimuthal quantum number, there are 2l +1 values of magnetic quantum
number.

Significance of magnetic quantum numbers:
1. It explain Zeeman effect.
2. It determines the number of orbitals present in any subshell. (2l +1 rule)
3. It gives information about space orientation of orbitals.

54. Spin quantum number (s):

It was introduced by Goudsmit and Uhlenbeck to explain double lines structure observed in the
spectrum of multi-electron system. It explains the spin angular momentum of electron. It is denoted
by 's' and can have +1/2 and -1/2 values, corresponding to clockwise and anticlockwise spin. +1/2
and -1/2 are often represented by arrow pointing up (↑) and down (↓) respectively. This quantum
number helps to explain magnetic properties of substance. A spinning electrons behaves like a
micro-magnet with definite magnetic moments. If an orbital contains two electrons, the two
magnetic moments oppose and cancel each other. Electron pair in an orbital is represented as ↑ ↓.

In an atom, if all the orbitals are completely filled, the net magnetic moment is zero. So the
substance is diamagnetic. In an atom, if some orbitals are partially filled, the substance has a
magnetic moment and is paramagnetic.

Significance of spin quantum number:
1. It explains double line structure observed in the spectrum of multi-electron atom.
2. It tells about the direction of electron spin like clockwise or anticlockwise.
3. It explains the magnetic properties of the substances.

55. Write short notes on quantum numbers.
 Quantum numbers are those numbers which are used to characterize the state of an
electron in an atom. Electrons in an atom are completely described by the set of four
quantum numbers. The four quantum numbers are;
1. Principal quantum number: It is introduced by Neil Bohr. It represents the main shell or energy level
around the nucleus. It specifies the location and energy of electron in an atom. It is denoted by 'n' and
its values are 1, 2, 3, 4 … or denoted by K, L, M, N …… E .It permits the electrons in different shells
according to 2n2
rule. Thus the first, second, third, fourth and fifth shell can accommodate 2, 8, 18, 32
and 50 electrons respectively.
2. Azimuthal quantum number: It is introduced by Somerfield to explain the fine lines observed with
high power spectroscope. It represents the sub-shell of the main shell. It describes the shape of the
sub-shell (orbital) in which the electron is located. It is also called subsidiary quantum number. The
sub-shells are designated by s, p, d and f. It is denoted by 'l'. Its value depend on the principle
quantum number and ranges from 0 to (n-1). Subshells with n= 0,1,2,3 are designated as s,p,d and f
orbitals respectively. It permits electrons in different orbital according to 2(2l+1) rule. Thus first shell
has only one sub-shell, second shell has two sub-shells, and third shell has three sub-shells and so on.
3. Magnetic quantum number: It was introduced by Linde to explain Zeeman effect. It represents the
orientation of the orbitals in space in presence of magnetic field. It is denoted by 'm' .Its values
depend on the azimuthal quantum number and ranges from +l to –l including 0. For ever 'l' values of
azimuthal quantum number, there are 2l +1 values of magnetic quantum number.
4. Spin quantum number: It was introduced by Goudsmit and Uhlenbeck to explain double lines
structure observed in the spectrum of multi-electron system. It explains the spin angular momentum
of electron. It is denoted by's' and can have +1/2 and -1/2 values, corresponding to clockwise and
anticlockwise spin. +1/2 and -1/2 are often represented by arrow pointing up (↑) and down (↓)
respectively.

56. Do yourself:
20.For n =3, write all possible values of l and m.
21.How many maximum number of electrons that may be present in principle
quantum number 3 and azimuthal quantum number 2?
22.What is (2l +1) rule?
23.What is 2(2l+1) rule?
24.For n =4, write all possible values of l and m.
25.What are the values of principle quantum for atom having atomic number =11?
26.Give the values of all four quantum number of 11th
electron of Magnesium (At.
No=12)
27.What are the values of n, l and m for 2px orbital?
28.An electron of an atom possesses the quantum numbers n=2, l =0 and m=0.
What do they mean?

57. Solved questions:
 (2l +1) rule: For a particular value of azimuthal
quantum number(l), there are 2l +1 value of
magnetic quantum number(m). This is called 2l +
1 rule.
 Example: for l= 1, m= 2x1+1= 3 values
 2(2l+1) rule: The maximum number of electron
that can be accommodated in a particular value
of l i.e., a subshell is given by 2(2l+1) rule.
 Example: for l=2(d-orbital), maximum number of
electron accommodated= 2(2x2+1)= 10 electrons

58. ELECTRONIC CONFIGURATION:
Three important rules governing the filling up of orbital
with electrons are as follow:
1. Bohr-Burry Scheme
2. Aufbau Principle
3. Hund’s rule

59. BOHR-BURRY SCHEME
Electrons are filled according to 2n2
rule.
Maximum number of electrons in various shells
Principle Quantum
number(n)
Shell Maximum no of
electrons(2n2
)
1 K 2
2 L 8
3 M 18
4 N 32
29. What is 2n2
rule? Write its limitation.

60. ..
 The maximum number of electron that can be
accommodated in a particular shell is given by 2n2
formula
where n is principal quantum number.
 Example: for n=1(K-shell), the maximum number of
electron=2x1 =2 electrons
 Limitations:
 The valence shell should not have more than 8 electrons.
 The penultimate shell (second last shell) should not have
more than 18 electrons.
 It is not necessary for an orbit to be completely filled
before the next orbit starts filling. In fact, a new shell
begins when the outermost orbit gets 8 electrons.

61. AUFBAU PRINCIPLE:
The atomic orbitals are filled up in the ground state in order of increasing energy levels.
This means that in the ground state of an atom, the electron enters the orbital of
lowest energy first. The energy levels of various orbitals are determined by the sum of
the principle quantum number 'n' and the azimuthal quantum number 'l'. This is known
as (n+l) rule. Hence the sequence of filling the orbitals proceeds as follow.
i. Orbitals are filled in order of increasing value of (n+l). For instance, for 4s orbitals,
(n+l) = 4+0=4, and for 3d orbitals, (n+l) = 3+2=5. Hence 4s orbitals is filled up before
3d orbital.
ii. For the orbitals having the same value of (n+l), the one having the lower value of n is
filled first. For instance, 2p orbital (n+l=2+1=3 and 3s orbital (n+l) =3+0 =3 have the
same value of (n+l). But, since 2p orbital has lower value of n, it is filled before 3s
orbital.
Following these rule, the sequence of filling of orbitals is 1s,2s,2p,3s,3p,3d..

62. Do yourself:
30.What is n+l rule? Give example.
31.Arrange the following orbitals in order of increasing
energy level: 3s, 3p, 3d, 4s
32.What is the sequence of filling the following atomic
orbital? 4s, 4d, 4p, 5f

63. Electronic configuration of atoms

1 Hydrogen 1s1

2 Helium

3 Lithium

4 Beryllium

5 Boron

6 Carbon

7 Nitrogen

8 Oxygen

9 Fluorine

10 Neon

11 Sodium

12 Magnesium

13 Aluminum

14 Silicon

15 Phosphorus

16 Sulphur

17 Chlorine

18 Argon

19 Potassium

20 Calcium

21 Scandium

22 Titanium
23 Vanadium

24 Chromium

25 Manganese

26 Iron

27 Cobalt

28 Nickel

29 Copper

30 zinc

64. Exception to Aufbau’s Principle
The exceptions to the above rule are
 Chromium 1s2
,2s2
,2p6
,3s2
,3p6
,4s1
,3d5
 Copper 1s2
,2s2
,2,3d10
These abnormalities are attributed to the fact that half
filled and completely filled d-orbitals have lower energy or
posses some extra stability..

65. Do yourself:
33. Write the electronic configuration of the element with atomic number 18 and
26.
34. Write the electronic configuration of Cr++
and O--
.
35. What is the maximum number of electrons that may be present in all the
atomic orbitals with principle quantum number (n=4) and azimuthal
quantum number (l=3)
36. An atom A has atomic number (Z=29). Calculate the total number of s
electrons of A++
.
37. Write the electronic configuration of the atom having atomic number 19.
What are the values of n, and l of its outermost electron?
Electronic configuration=1s22s22p63s23p64s1
Outermost electron is 4s1
n=4, l=0

66. Do yourself:
38. Give the electronic configuration of Copper (At no 29) in term of s, p, d, f orbital.
39. Give the electronic configuration of silver (At no 47) in term of s, p, d, f orbital.
40. A scientist investigating the structure of the element concluded that the K, L, and M
shells were all full and that the N shell contained 4 electrons. What is the atomic
number of that element? Write the electronic configuration.
41. Write the electronic configuration of elements with the atomic number 19 and 24. Give
the name of these elements.
42. Write the electronic configuration of Cu++
and Fe+++
.
43. Give the electronic configuration of chromium (At. no 24) in term of s, p, d, f orbital.
44. Write the atomic number of elements whose outermost electronic configuration are
represented by (a) 3s1
(b) 3p6
45. An element has 2 electrons in K shell, 8 electrons in L shell and 9 electrons in M shell.
Write the electronic configuration and calculate the total numbers of p-electrons.

67. HUND’S RULE OF MAXIMUM MULTIPLICITY
 The orbitals with equivalent energy are called degenerate orbitals. Examples;
 3Px, 3py, and 3pz are degenerate orbitals.
 4dxy, 4dyz, 4dzx, 4dz2, 4dx2-y2 are degenerate orbitals
Electrons will distribute themselves in degenerate orbitals so as to retain parallel spin as
much as possible.
Or
Electrons do not pair up until they have to.
According to Hund’s rule while filling up electrons in degenerate orbitals, electrons first fill
up singly then only starts to pair up. It means atomic orbitals tends to have more number
of unpaired electrons as far as possible. Greater number of unpaired electrons offer
maximum multiplicity
The electronic configuration of C, N and O can be written as:

69. Pauli's Exclusion Principle:
"No two electron in an atom have same set of four
quantum numbers."

70. Pauli's Exclusion Principle:-Illustration:
 He= 1s2
 In He atom, the value of n, l and m are same but
the value of s is different.
Electron n l m s
1st
electron
1 0 0 +1/2
2nd
electron
1 0 0 -1/2

71. Quantum numbers for Carbon
atom
 Carbon= 1s2
2s2
2p2
Electron n l m s
1s 1 0 0 +1/2
1 0 0 -1/2
2s 2 0 0 +1/2
2 0 0 -1/2
2p 2 1 -1 +1/2
2 1 +1 +1/2

72. Discussion and Additional Questions:

73. Atomic Structure
Discussion Questions / Homework
1.Rutherford’s nuclear model of atom is
based on alpha particles scattering
experiment.
a. What are alpha particles?
b. Why did Rutherford select gold for
his experiment? Suggest.

74. 2.While Bohr’s atomic theory introduced the concept of
orbit, wave mechanical model (de broglie’s equation and
Schrodinger’s wave equation) introduced the concept of
probability, the orbitals.
a. Explain on the basis of Bohr’s why is it that electrons do
not jump into the nucleus?
b. Which principle goes against the concept of Bohr's fixed
orbits?
c. What is matter wave? How is the wave length of matter
wave determined?
d. Why is Hund’s rule called the rule of maximum
multiplicity?

75. 3.When high electric discharge is passed through hydrogen
molecule at low pressure, hydrogen spectra is formed.
a. Name the spectral series which appears visible part of
the electromagnetic spectrum. How is such series
originated?
b. Why does hydrogen gas show large number of line
spectra though hydrogen atom contains one electron?

76. 4.According to Aufbau’s principle, electrons are filled up in ground
state in order of increasing energy level.
a. How is orbital different from orbit?
b. Arrange the following orbitals in order of increasing energy level:
3s, 3p, 3d, 4s
c. What is the sequence of filling the following atomic orbital? 4s, 4d,
4p, 5f
d. Write the electronic configuration of Cr++
and O- -
.
e. Give the electronic configuration of chromium (At. no 24) and
Copper (At no 29) in term of s, p, d, f orbital.
f. Write the electronic configuration of elements with the atomic
number 19 and 24. Give the name of these elements.
g. Write the atomic number of elements whose outermost electronic
configuration are represented by (a) 3s1
(b) 3p6
h. Write the electronic configuration of Cu++
and Fe+++
. Also calculate
the number of unpaired electron in each case.
i. An atom A has atomic number (Z=29). Calculate the total number of
s electrons of A++
.

77. 5.An atom consists of a large number of orbitals. Different orbitals are distinguished
from each other on the basis of shape, size and orientation in space. These are
explained on the basis of quantum numbers.
a. An electron of an atom possesses the quantum numbers n=2, l =0 and m=0. What
do they mean?
b. For n =4, write all possible values of l and m.
c. Determine the value of l and m for 3d and 4p orbitals
d. Determine the value of l, m and s for 4s1
, 3p1
, 4p2
, 2p3
and 4p4
orbitals.
e. How many maximum number of electrons that may be present in principle
quantum number 3 and azimuthal quantum number 2?
f. What are the values of principle quantum for atom having atomic number =11?
g. Give the values of all four quantum number of 11thelectron of Magnesium (At.
No=12)
h. Write the electronic configuration of the atom having atomic number 19. What
are the values of n, and l of its outermost electron?

78. 6.An element has 2 electrons in K shell, 8
electrons in L shell and 9 electrons in M shell.
Find out the following:
a. Electronic configuration of the atom
b. Total number of principal quantum number
c. Total number of subshell
d. Total numbers of s, p and d-electrons.
e. Number of unpaired electrons

79. Additional Practice Questions:
1. What experimental evidence led Rutherford to conclude that?
a. The nucleus of an atom contains most of the atomic mass
b. The nucleus of an atom is positively charged
c. The atom consists of mostly empty space.
2. Why electron does not fall into the nucleus? Write the
shortcomings of nuclear model.

80. 3. The arrangement of orbitals on the basis of energy is based upon their
(n+l) value.
a. State the principle which explain this rule.
b. An atom has 2, 8 and 2 electrons in K, L, and M shells respectively.
Find out the followings.
i. electronic configuration of the atom.
ii. total number of principal quantum numbers.
iii. total number of sub shells and number of s electron
c. Briefly, discuss the quantum number which introduce the sub-shell
and orbitals.
d. Based upon the above information, which of the following orbitals
has the lowest energy? Give reason.
4d, 4f, 5s, 5p
e. How many electrons could be held in the second shell of an atom, if
the spin quantum numberms could have three values instead of just two?

81. 4. Bohr’s atomic theory is able to explain the
stability of atom as well as the formation of
hydrogen spectra.
a. How does this theory explain the stability
of atom?
b. Draw a labeled diagram to show different
spectral series of hydrogen spectra.
c. Which principle goes against Bohr’s
theory? State the principle.

82. 5. An element “A” has 2 electrons in K-shell,
8 electrons in L shell and 5 electrons in M
shell.
i. Identify the element “A” and write the
number of protons and electrons in it.
ii. Size of X- - -
ion is greater than that of “A”
atom through both contain the same number
of protons. Give reason.
iii. write down the formula of one of the
compounds of A where A is in -3 oxidation
state.

83. 6. Different model was put forward to explain the structure
of atom, one of them is nuclear model of atom.
a. How is nuclear model of atom is improved by Bohr?
b. How did it overcome the limitations of nuclear model of
atom?
c. Write the electronic configuration of iron in Fe(OH)3 and
Fe(OH)2.
d. How many orbitals are present in the M-shell?

84. 7. Quantum number are the number which give the
complete information of electron in an atom.
a. Explain the quantum numbers which specifies the
shape of orbitals and main energy of an atom.
b. A scientist investigating atomic structure of the
element concluded that the K, L, & M shell were all
full and that the N shell contained four electrons.
What is the atomic number of the element?
c. State the Hund’s rule with suitable example? Why
is Hund’s rule called rule of maximum multiplicity?
d. Give the values of all four quantum of 11th
electron
of Magnesium.

85. 8. Hydrogen gas show large number of line spectra though
hydrogen atom contains one electron.
a. What is meant by atomic spectrum? What is continuous and
discontinuous spectrum? Give example.
b. Draw the different spectral line obtained in Hydrogen spectrum.
c. Explain the spectral line observed in visible and infrared region.
d. State and explain de-Broglie’s wave particle duality concept.
e. State Pauli-exclusion principle.

86. 9. Bohr successfully explain the stability of atom by introducing the
stationary state and Hydrogen spectra.
a. State the principle which goes against the concept of Bohr’s fixed
concept. How would the velocity be affected if the position is known?
b. Write the drawbacks of the Bohr’s model.
c. Point out differences between the orbit and orbital. Sketch the shape
of s and p orbitals.
d. Write the atomic number of elements whose outermost electronic
configuration is represented by 3p6
.

87. 10. The valence shell electronic configuration of two atoms “X” and
“Y” are 4S1
and 3s2
3p5
respectively.
a. Write their atomic number.
b. Give the values of quantum number for the electron with highest
energy in sodium atom and for n=4, write all possible values of l and
m.
c. Write the electronic configuration of Cr +2
and Zn 2+.
Mention the
number of unpaired electrons in each case.
d. What do you mean by quantization of angular momentum?
e. An electron of an atom possesses the quantum number n = 2, l = 0
and m = 0. What do they mean?

88. 11. Orbital are the three-dimensional space around the nucleus,
where there is maximum probability of finding electrons.
a. Write the shapes of s and p orbital.
b. An Atom of element has 24 electrons, calculate the total
number of s and p electron?
c. What is meant by degenerate orbitals? Give suitable example
of it.
d. Name the quantum number that specifies the energy of an
electron in an atom. Calculate the values of quantum number m
and l of electrons for 3d and 3p orbitals.

89. 12. Each atomic orbital is characterized by three quantum numbers- n(principal ),
l(azimuthal) and m(magnetic).
a. For n =3, write all possible values of l and m.
b. Write the electronic configuration of the element with atomic number 18 and
26.
c. What is (2l +1) and 2(2l+1) rule?
d. Give the electronic configuration of silver (At no 47) in term of s, p, d, f
orbital.
e. What is the maximum number of electrons that may be present in all the
atomic orbitals with principle quantum number (n=4) and azimuthal quantum
number (l=3)