Asymmetric Encryption with RSA

$ 7absec
-- Aaftab Harun
(7absec)

$ 7absec
Introduction
Encryption V/S Encoding
Prime & Coprime
Encryption Process
Decryption Process
Conclusion
11:10 AM
11:20 AM
11:30 AM
11:40 AM
12:10 PM
12:20 PM

$ 7absec
Asymmetric cryptography, also known as public-key cryptography, is a process that
uses a pair of related keys -- one public key and one private key -- to encrypt and
decrypt a message and protect it from unauthorized access or use.

$ 7absec
RSA is an asymmetric public-key encryption system that is very commonly
used in real world applications.
The RSA Encryption algorithm is based primarily around the concept
of Coprimality.

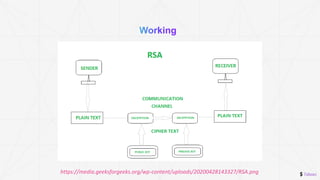
$ 7absec
https://media.geeksforgeeks.org/wp-content/uploads/20200428143327/RSA.png

$ 7absec
p = A prime number
q = A prime number
n = p * q
φ = (p - 1) * (q - 1)
e = public Key
d = Private Key
m = Message ( to encrypt/decrypt)
=== Co-prime Number

$ 7absec
• A Number that is only divisible by 1 and the number itself
• For instance 2,3,5,7,11, …
Walk Through
2: Coprime Number
3: Assigning values of p & q
4: Calculating n and phi
5: Progress upto this
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys
10: Encryption & Decryption

$ 7absec
• Two numbers having 1 as greatest common divisor (gcd)
• For instance 11 & 13, 8 & 15 etc
Walk Through
1: Prime Number
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys

$ 7absec
• RSA Key generation starts with two prime numbers.
• These can be randomly selected or otherwise — they
just have to be prime.
• P = 11
• Q = 13
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys

$ 7absec
• N is simply p and q multiplied together.
• n = p * q = 11 * 13 = 143
• Phi is the number of integers that are coprime to n
• phi = (p-1) * (q-1) = (11-1) * (13-1) = 120
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys

$ 7absec
RSA Encryption
• p = 11
• q = 13
• n = 143
• phi = 120
• e?
• d?
• m =“?”
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys

$ 7absec
• A number that is less than phi, and coprime to both n
and phi.
• The key should be greater than 2 and less than phi
(2<e<phi)
• n = 143
• phi = 120
• possible_bup_keys = []
• for i in range(2, phi):
• if gcd(n, i) == 1 and gcd (phi, i) == 1:
• possible_bup_keys.append(i)
• Print(possible_bup_keys)
Walk Through
1: Prime Number
2: Coprime Number
7: Finding “d”
9: Asymmetric Keys

$ 7absec
• A number that is grater than phi
• d*e mod phi = 1 or d*e % phi = 1
• phi = 120
• e = 7
• possible_pvt_keys = []
• for i in range(phi + 1, phi + 1000):
• if i * e % phi == 1:
• possible_pvt_keys.append(i)
• Print(possible_pvt_keys)
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
9: Asymmetric Keys

$ 7absec
RSA Encryption
P = 11
q = 13
n = 143
phi = 120
e = 7
d = 223
m= “ Hello”
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys

$ 7absec
• Public Key: (e, n)
• Private Key: (d, n)
• Public Key: (7, 143)
• Private Key (223, 143)
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
7: Finding “d”

$ 7absec
• Encryption
• m ** e % n
• Decryption
• enc_m ** d % n
Walk Through
1: Prime Number
2: Coprime Number
6: Finding “e”
7: Finding “d”
9: Asymmetric Keys

$ 7absec
• Asymmetric encryption is more secure than symmetric encryption.

$ 7absec
Questions/Suggestions…

Asymmetric Encryption with RSA

More Related Content

Similar to Asymmetric Encryption with RSA

Recently uploaded

Asymmetric Encryption with RSA