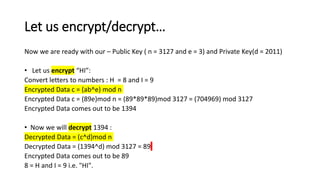
RSA is an asymmetric encryption algorithm that uses public and private key pairs for encryption and decryption. It involves key generation to create the public and private keys, and encryption and decryption functions that use the keys to scramble and unscramble data. Digital signatures generated using RSA can verify the authenticity of electronically sent messages.

1. RSA Encryption
• RSA is an asymmetric cryptography algorithm.
 Key Generation: Generating the keys to be used for encrypting and decrypting the data to be exchanged.
 Encryption/Decryption Function: The steps that need to be run when scrambling and recovering the data.
RSA Digital Signature
Digital signatures are used to verify the authenticity of the message sent electronically.
RSA – Rivest, Shamir, Adleman

2. What Is Asymmetric Encryption?

3. Public/Private Key Generation
• Public Key: Select two prime no's. Suppose P = 53 and Q = 59.
Now First part of the Public key : n = P*Q = 3127
Now z = (p-1)(q-1), Choose a number e where 1 < e < z. Let us now consider e as 3
c = (PQ^e) mod n
Our Public Key is made of n and e
• Private Key: We need to calculate Φ(n) :
Such that Φ(n) = (P-1)(Q-1)
so, Φ(n) = (53-1)(59-1)=(52)(58)=3016
Now calculate Private Key, d :
d = (k*Φ(n) + 1) / e for some integer k
For k = 2, d = (2*3016+1)/3 = (6032+1)/3 = (6033)/3 = 2011
value of d is 2011.

4. Let us encrypt/decrypt…
Now we are ready with our – Public Key ( n = 3127 and e = 3) and Private Key(d = 2011)
• Let us encrypt “HI”:
Convert letters to numbers : H = 8 and I = 9
Encrypted Data c = (ab^e) mod n
Encrypted Data c = (89e)mod n = (89*89*89)mod 3127 = (704969) mod 3127
Encrypted Data comes out to be 1394
• Now we will decrypt 1394 :
Decrypted Data = (c^d)mod n
Decrypted Data = (1394^d) mod 3127 = 89
Encrypted Data comes out to be 89
8 = H and I = 9 i.e. "HI".

5. RSA Digital Signature

6. RSA Digital Signature…

7. Code pointers
• integ_rsa_encrypt.c
• integ_rsa_decrypt.c
• integ_rsa_keygen.c
typedef struct _CpaCyRsaKeyGenOpData {
CpaFlatBuffer prime1P;
CpaFlatBuffer prime2Q;
Cpa32U modulusLenInBytes;
CpaCyRsaVersion version;
CpaCyRsaPrivateKeyRepType privateKeyRepType;
CpaFlatBuffer publicExponentE;
} CpaCyRsaKeyGenOpData;
Integ code
isg_cid_qat_sal/me_acceleration_layer/access_layer/look_aside_acceleration/integ_test/common/crypto/asym/rsa
typedef struct _CpaCyRsaEncryptOpData {
CpaCyRsaPublicKey *pPublicKey;
/**< Pointer to the public key. */
CpaFlatBuffer inputData;
/**< The input data that the RSA encryption primitive operation is
* performed on. The data pointed to is an integer that MUST be in big-
* endian order. The value MUST be between 0 and the modulus n - 1. */
} CpaCyRsaEncryptOpData;
typedef struct _CpaCyRsaDecryptOpData {
CpaCyRsaPrivateKey *pRecipientPrivateKey;
/**< Pointer to the recipient's RSA private key. */
CpaFlatBuffer inputData;
/**< The input data that the RSA decryption primitive operation is
* performed on. The data pointed to is an integer that MUST be in big-
* endian order. The value MUST be between 0 and the modulus n - 1. */
} CpaCyRsaDecryptOpData;

8. Code pointers…
Key Generation
LacIntegRsa_AllocKeyGenData
-LacIntegPke_CreatePrivateKey
-LacIntegPke_CreatePublicKey
LacIntegRsa_KeySendReq
-LacIntegRsa_KeySend
-cpaCyRsaGenKey -> SAL code
Encryption
LacIntegRsa_EncryptInt/LacIntegRsa_EncPerfTestInt
-LacIntegRsa_AllocEncData
-LacIntegPke_CreatePublicKey
-LacIntegPke_PopulateFlatBuffer
LacIntegRsa_EncPerfTestInt
-LacIntegRsa_EncSendReq
-LacIntegRsa_EncSend
-cpaCyRsaEncrypt ->SAL code
Decryption
LacIntegRsa_Decrypt1Int
->LacIntegRsa_AllocDec1Data
->LacIntegPke_CreatePrivateKey1
->LacIntegPke_PopulateFlatBuffer
LacIntegRsa_DecPerfTestInt
LacIntegRsa_DecSendReq
->LacIntegRsa_DecSend
->cpaCyRsaDecrypt -> SAL code