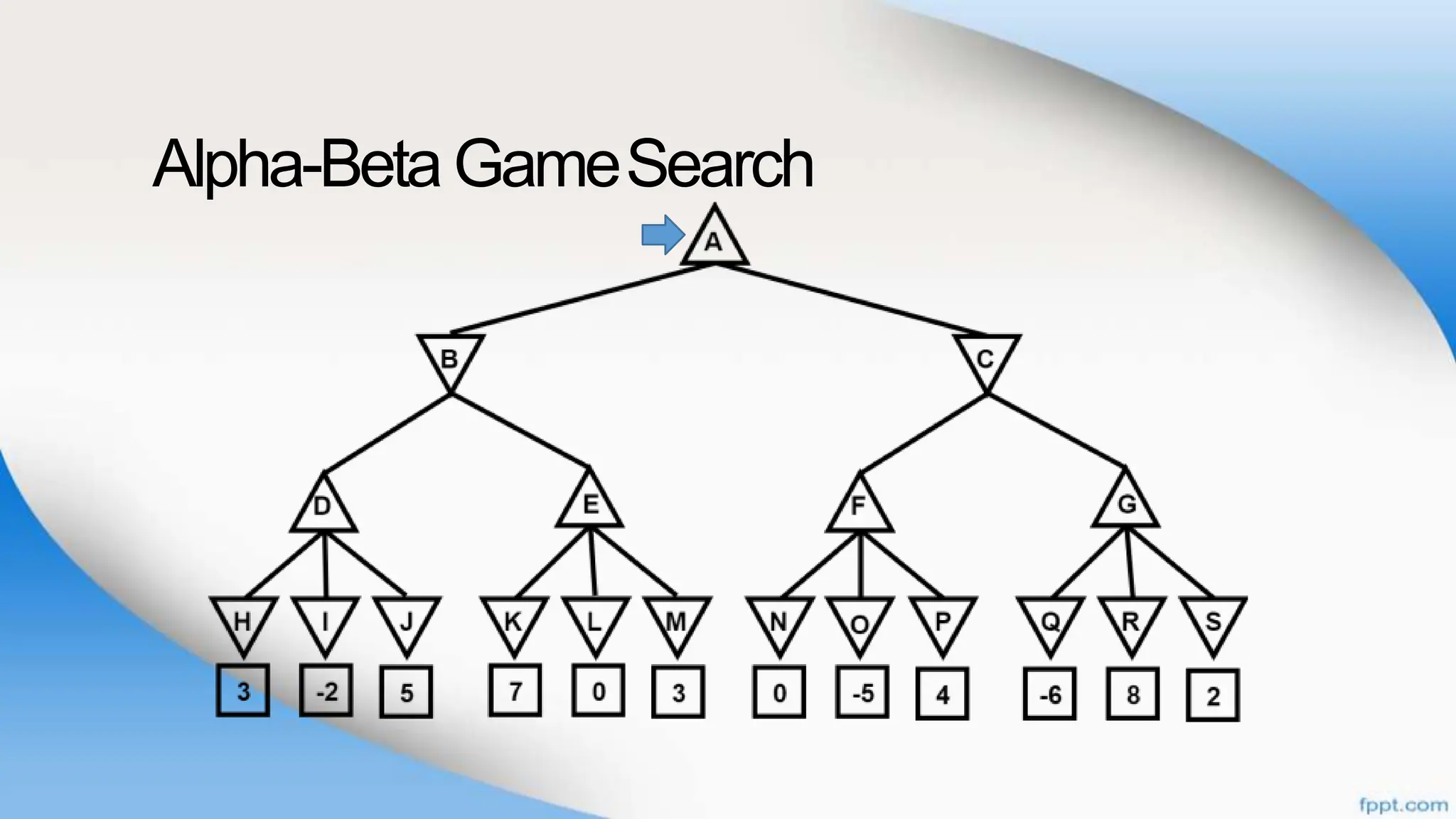
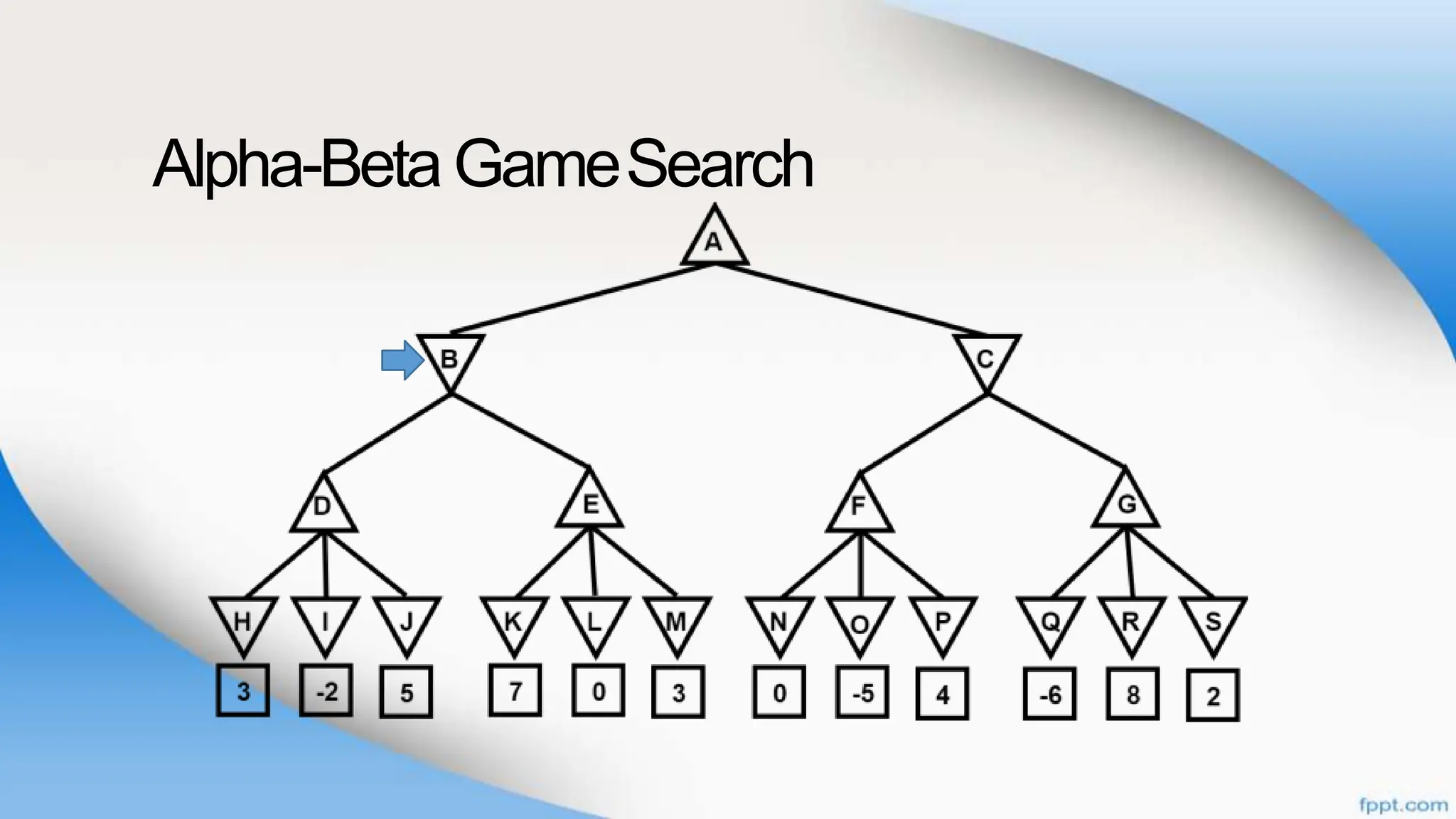
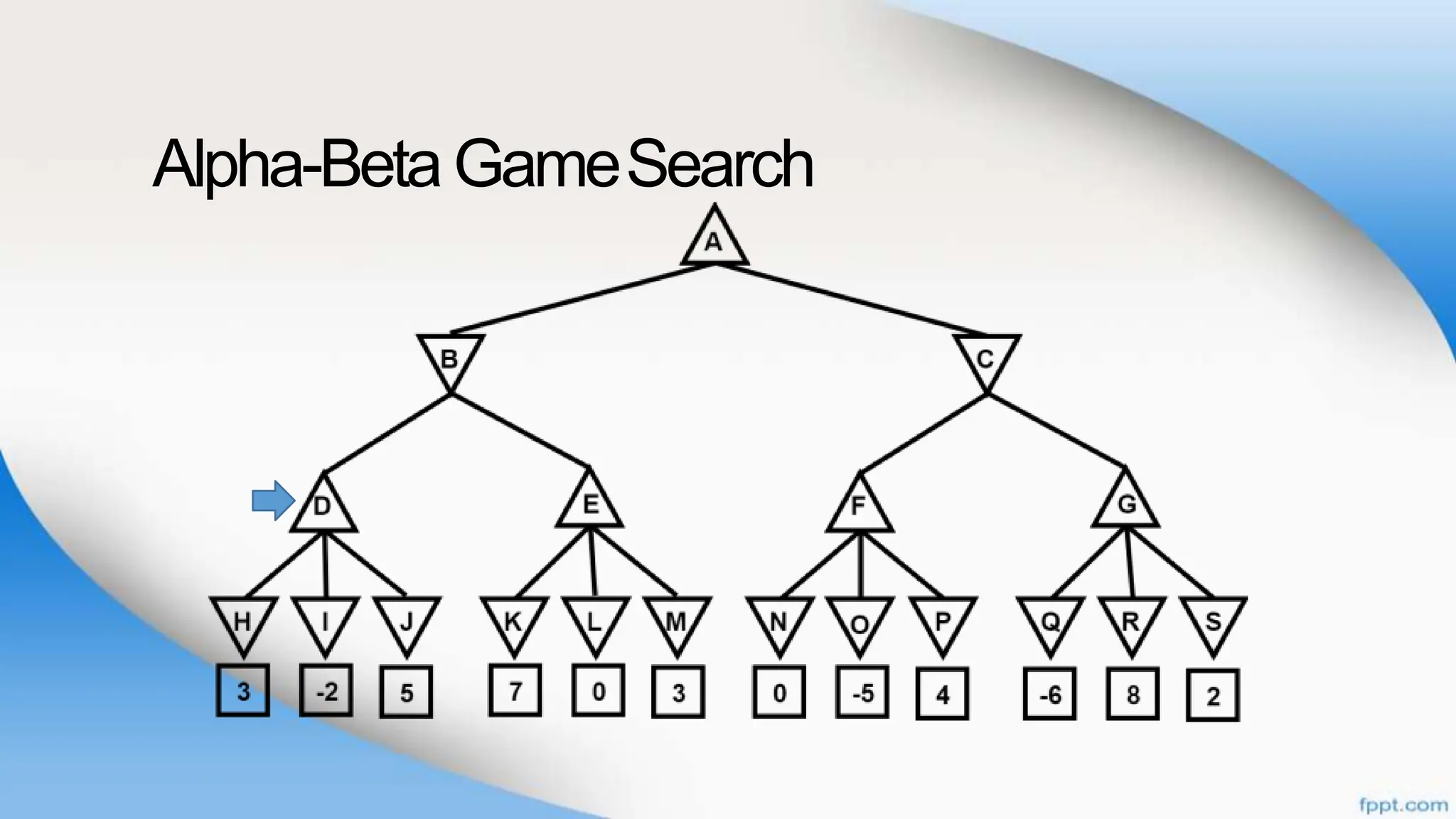
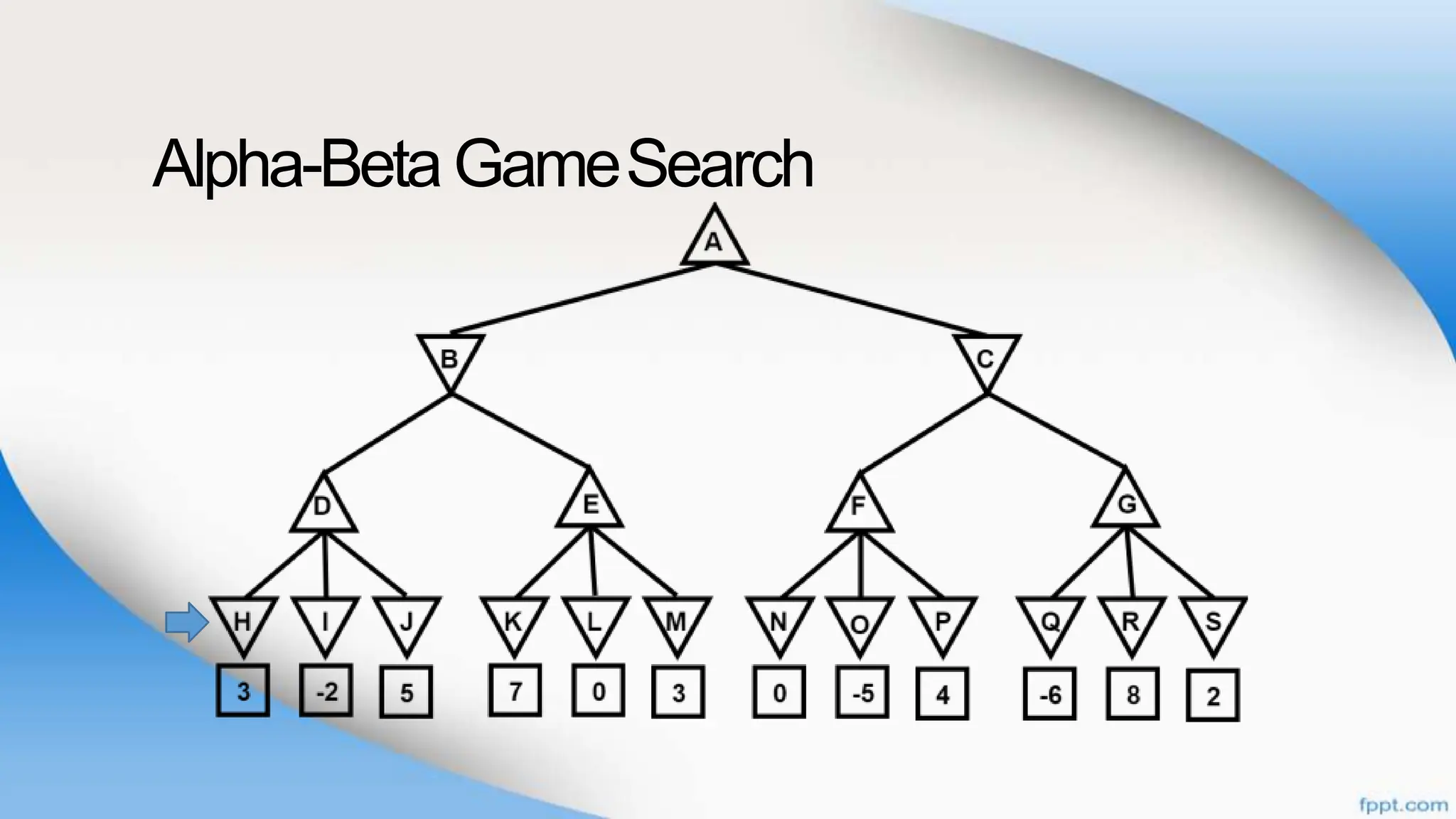
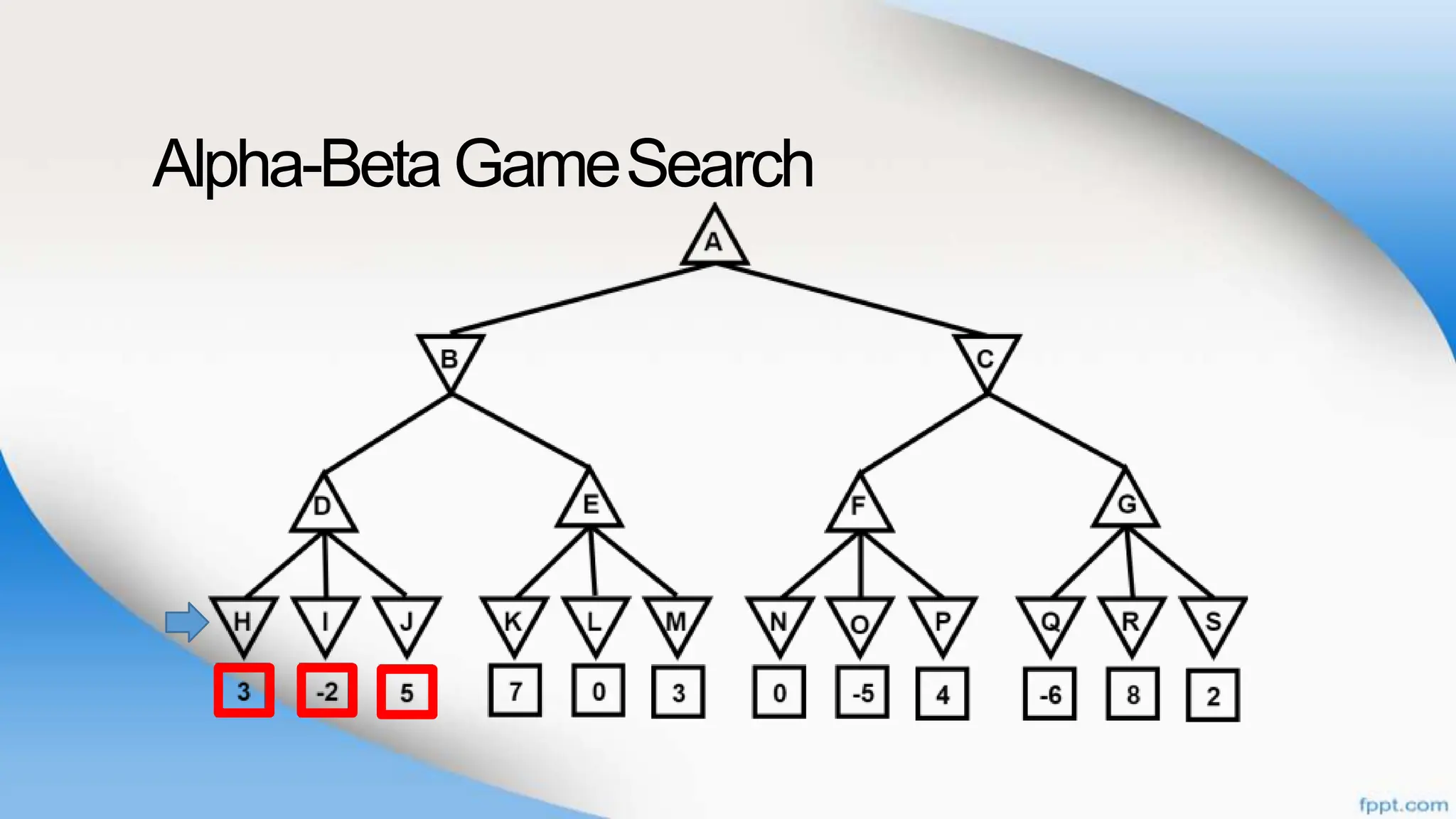
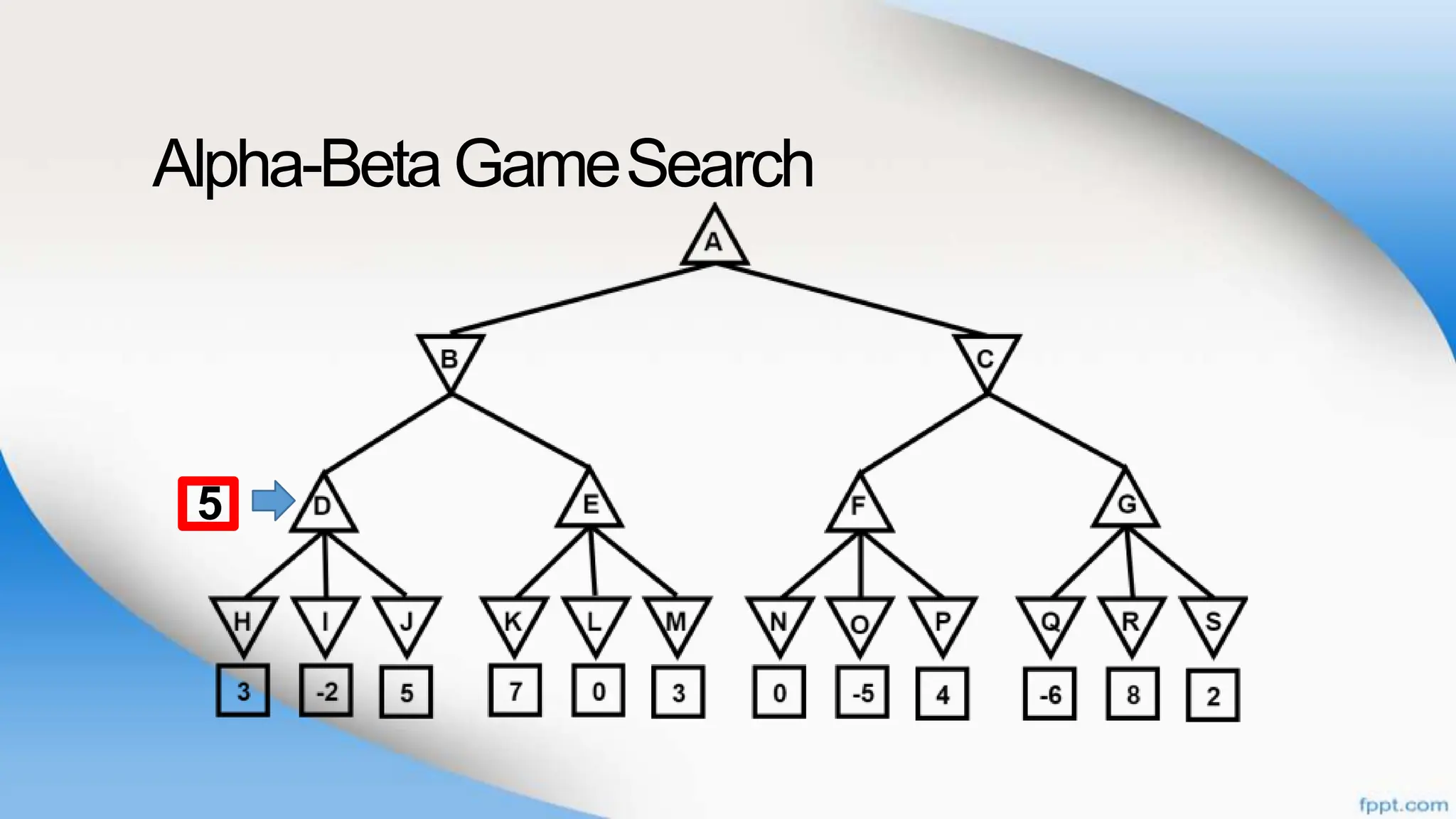
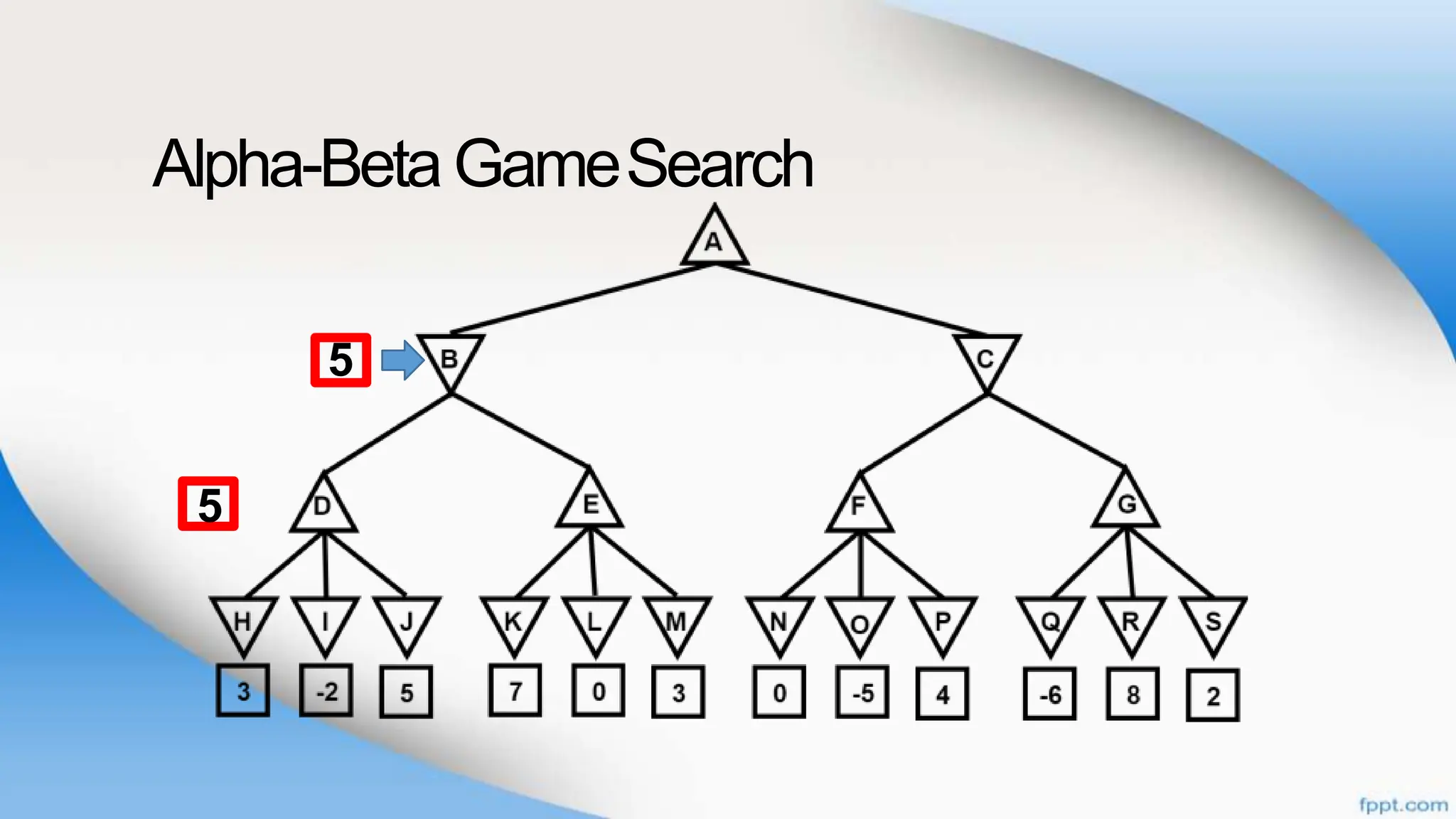
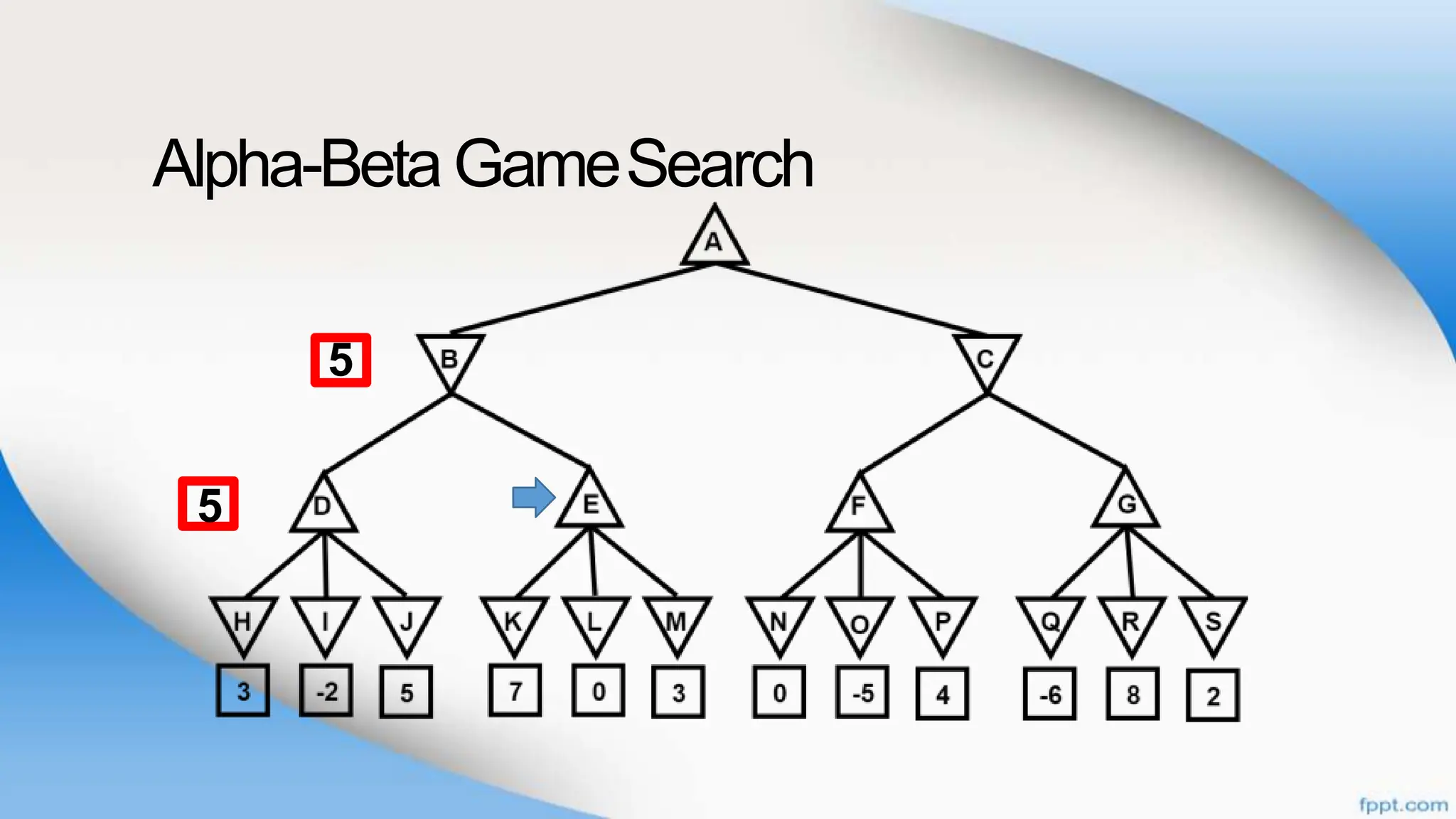
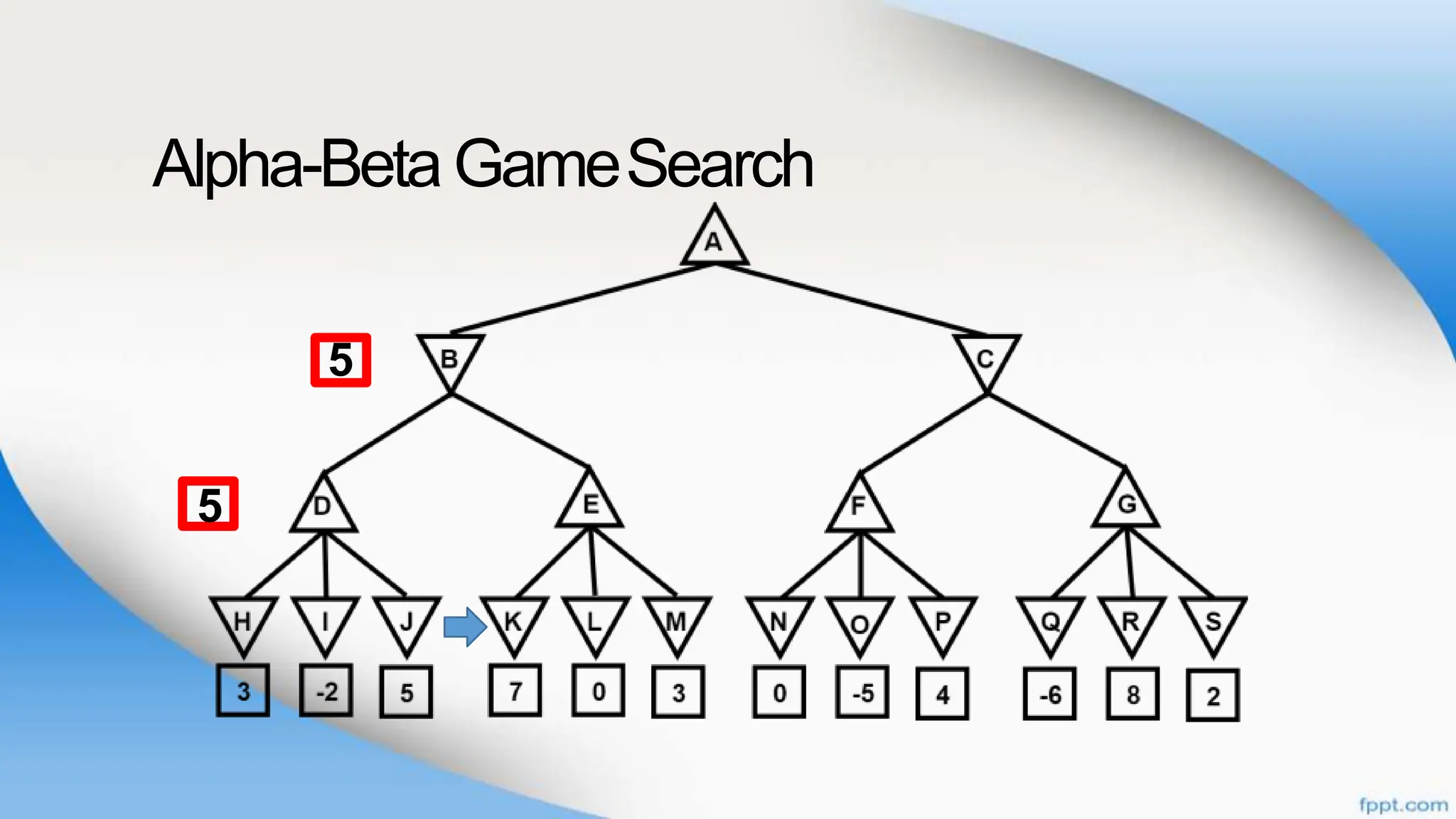
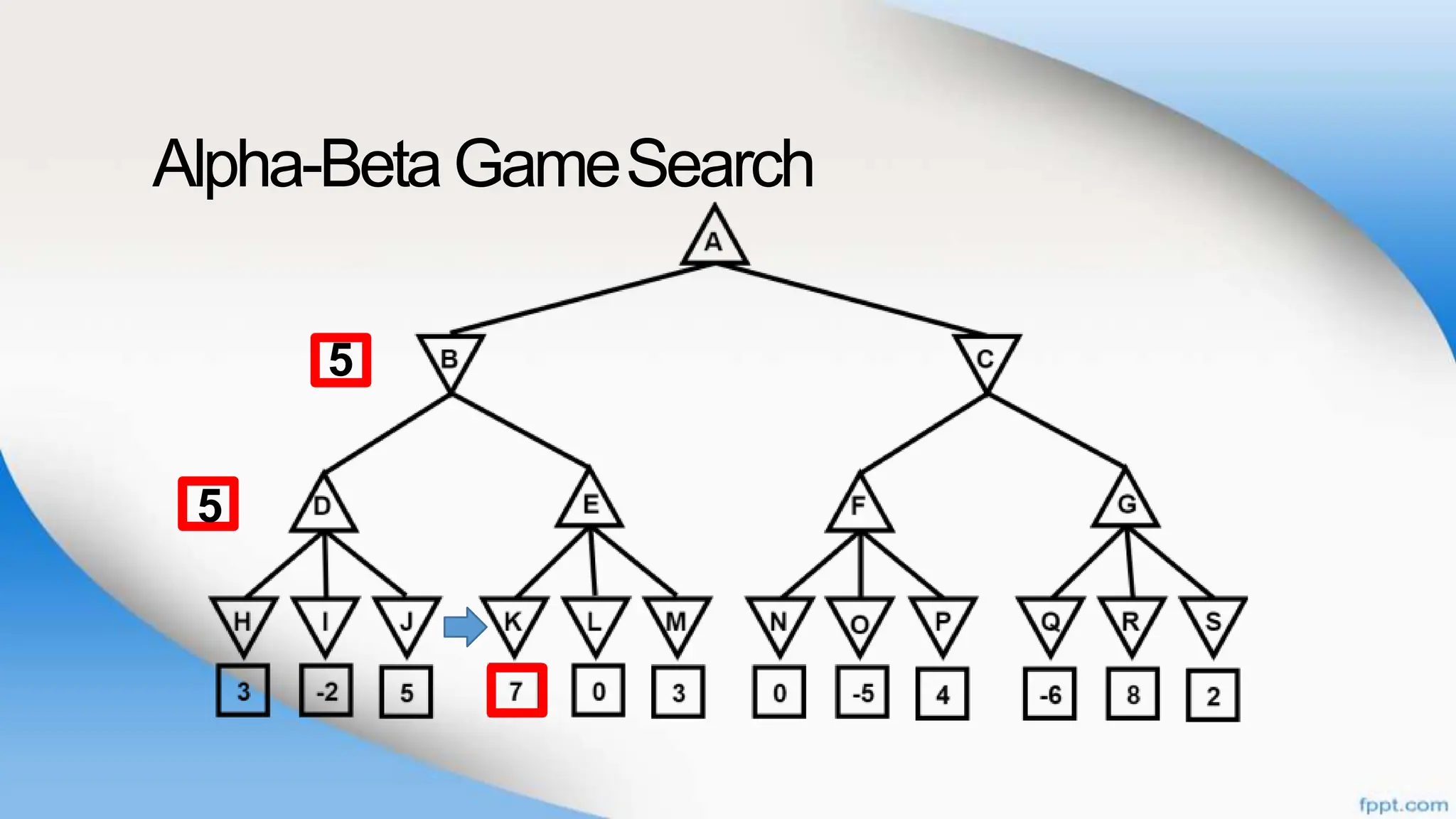
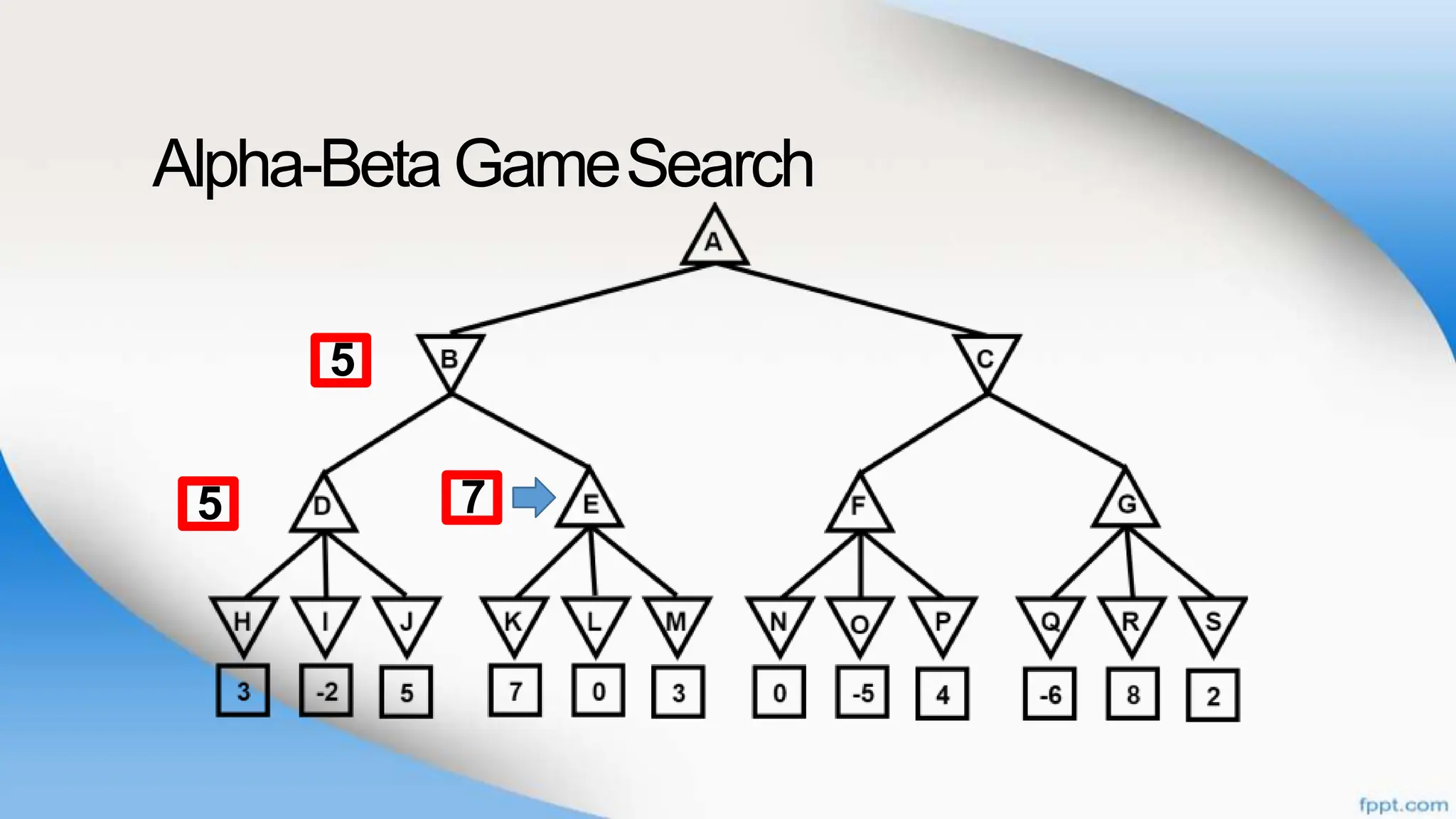
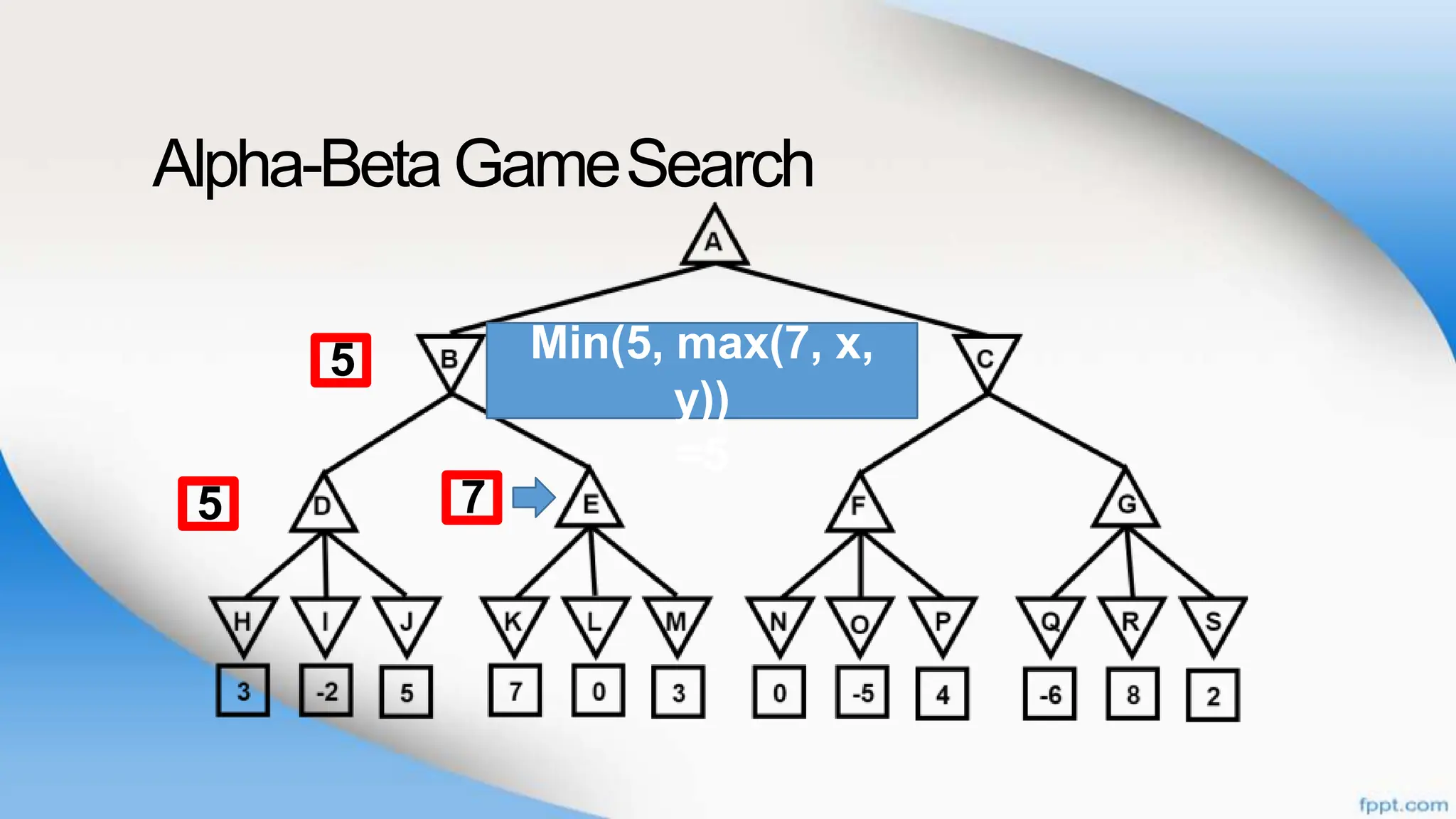
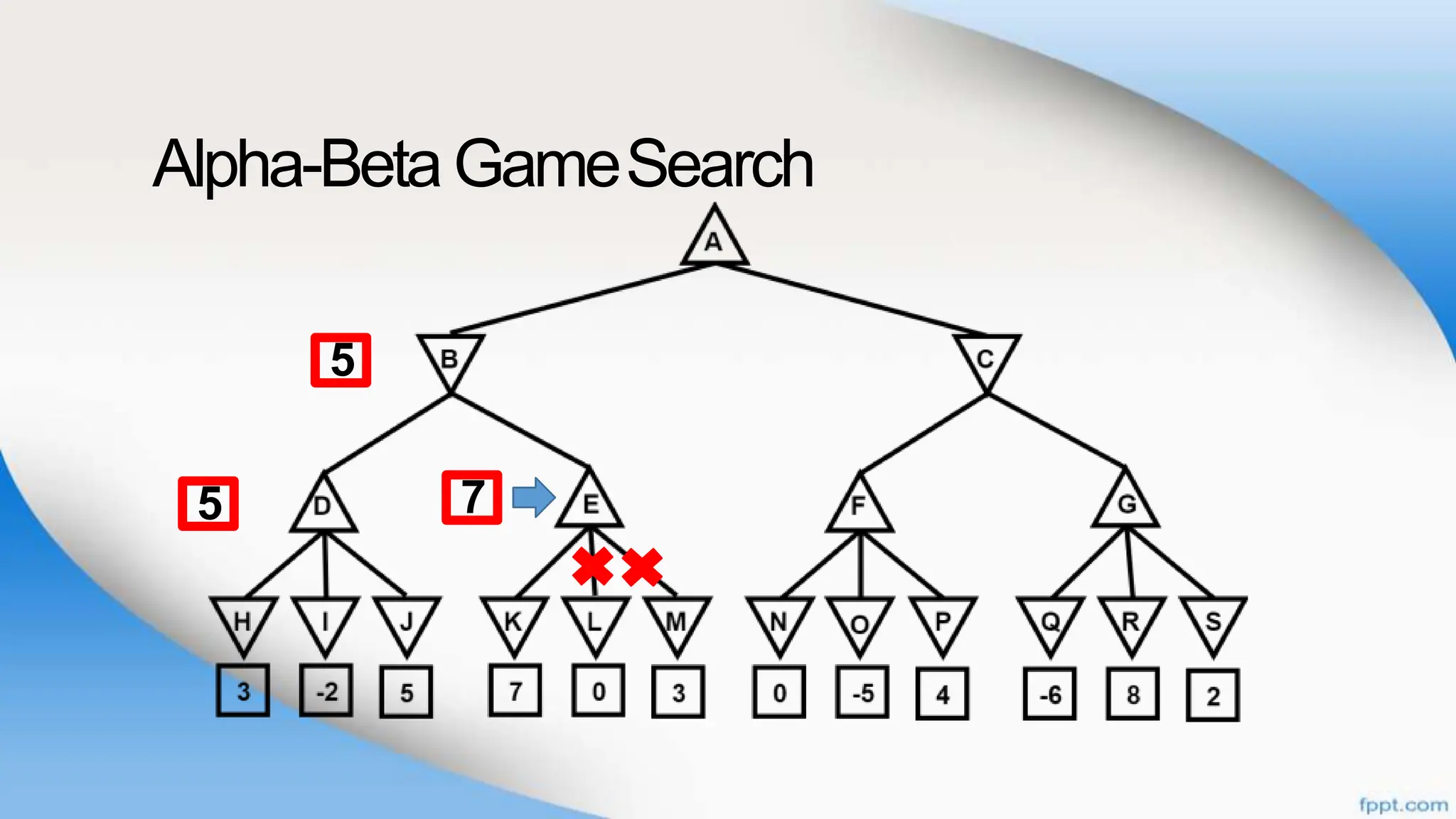
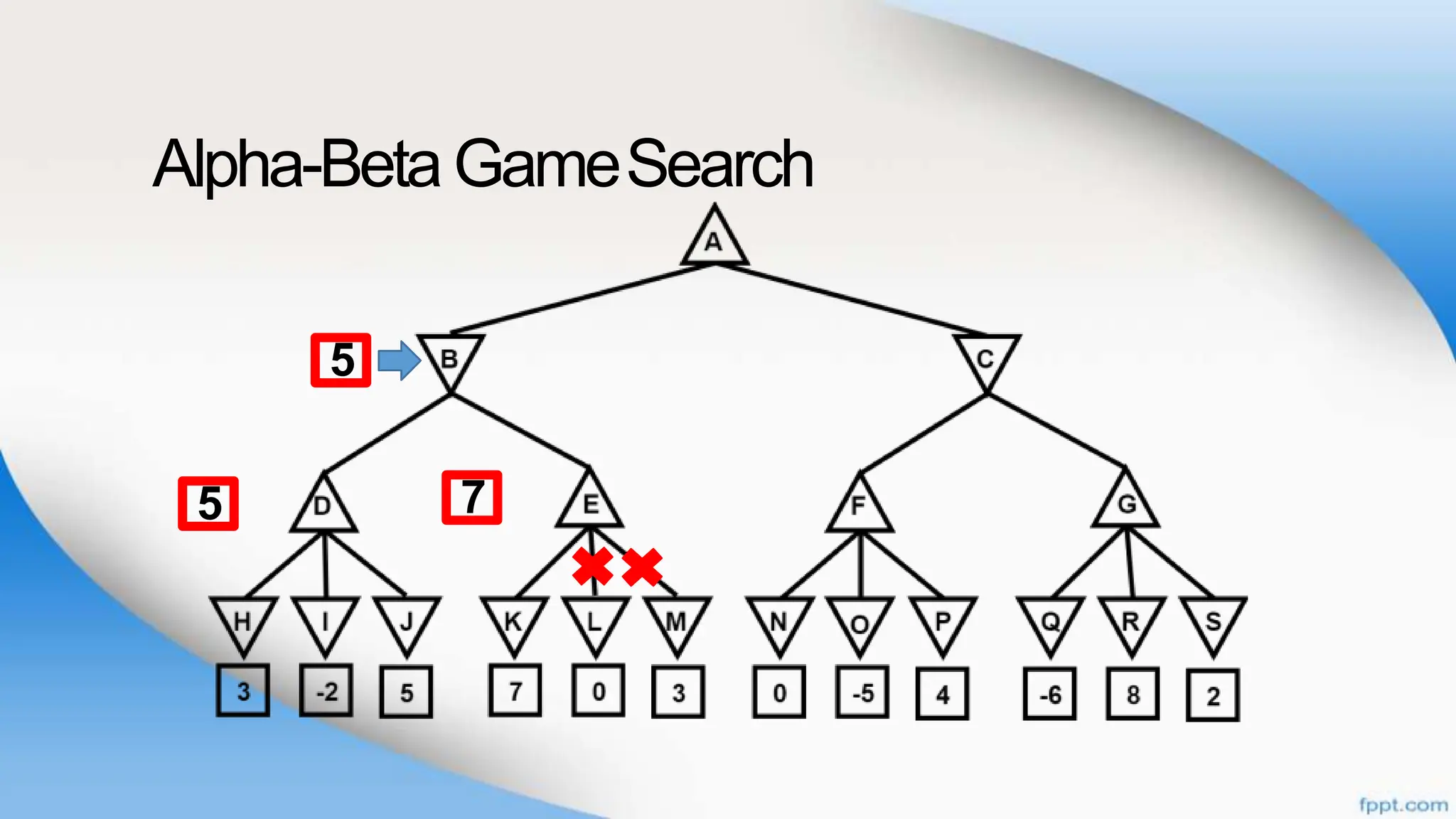
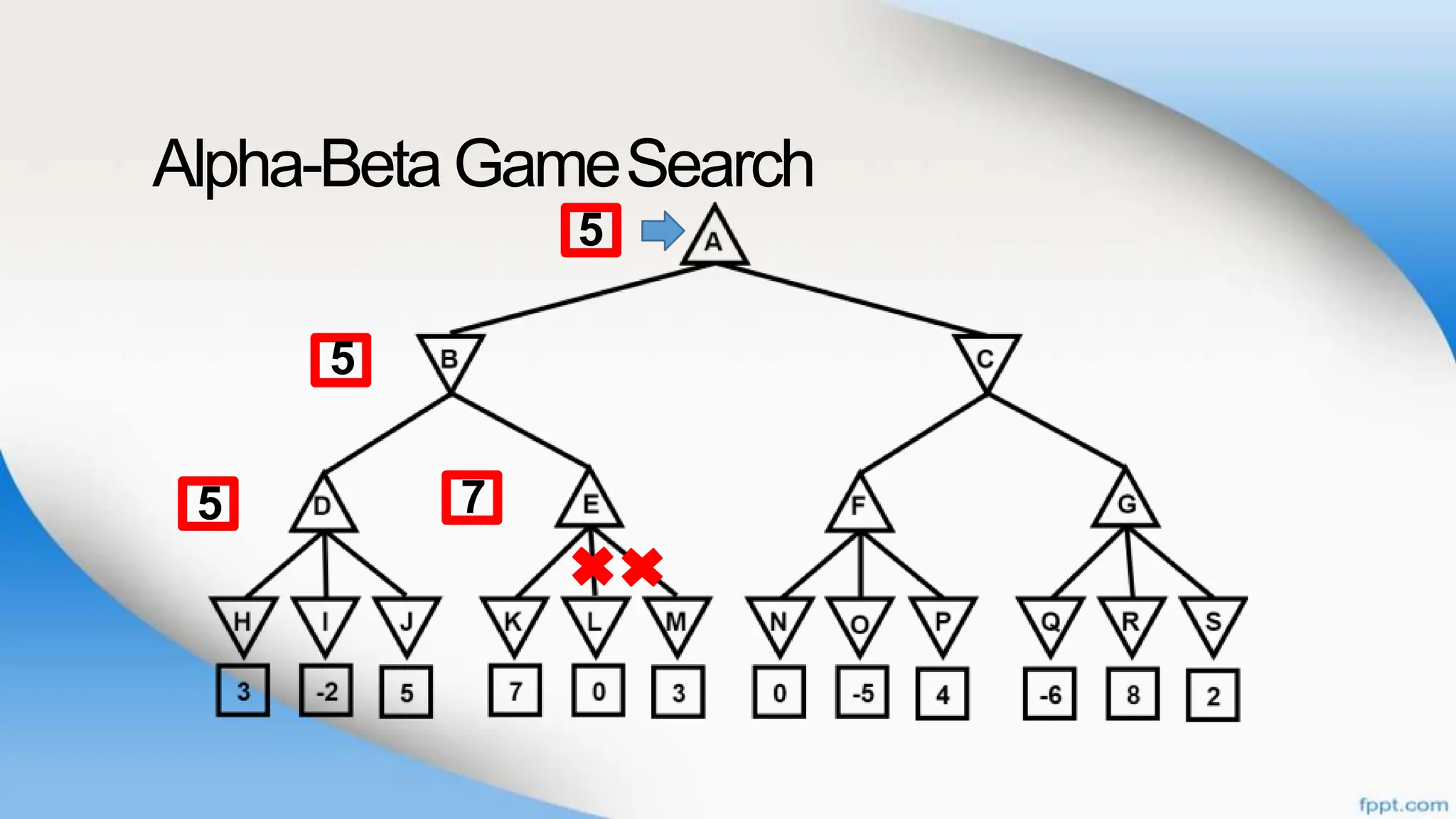
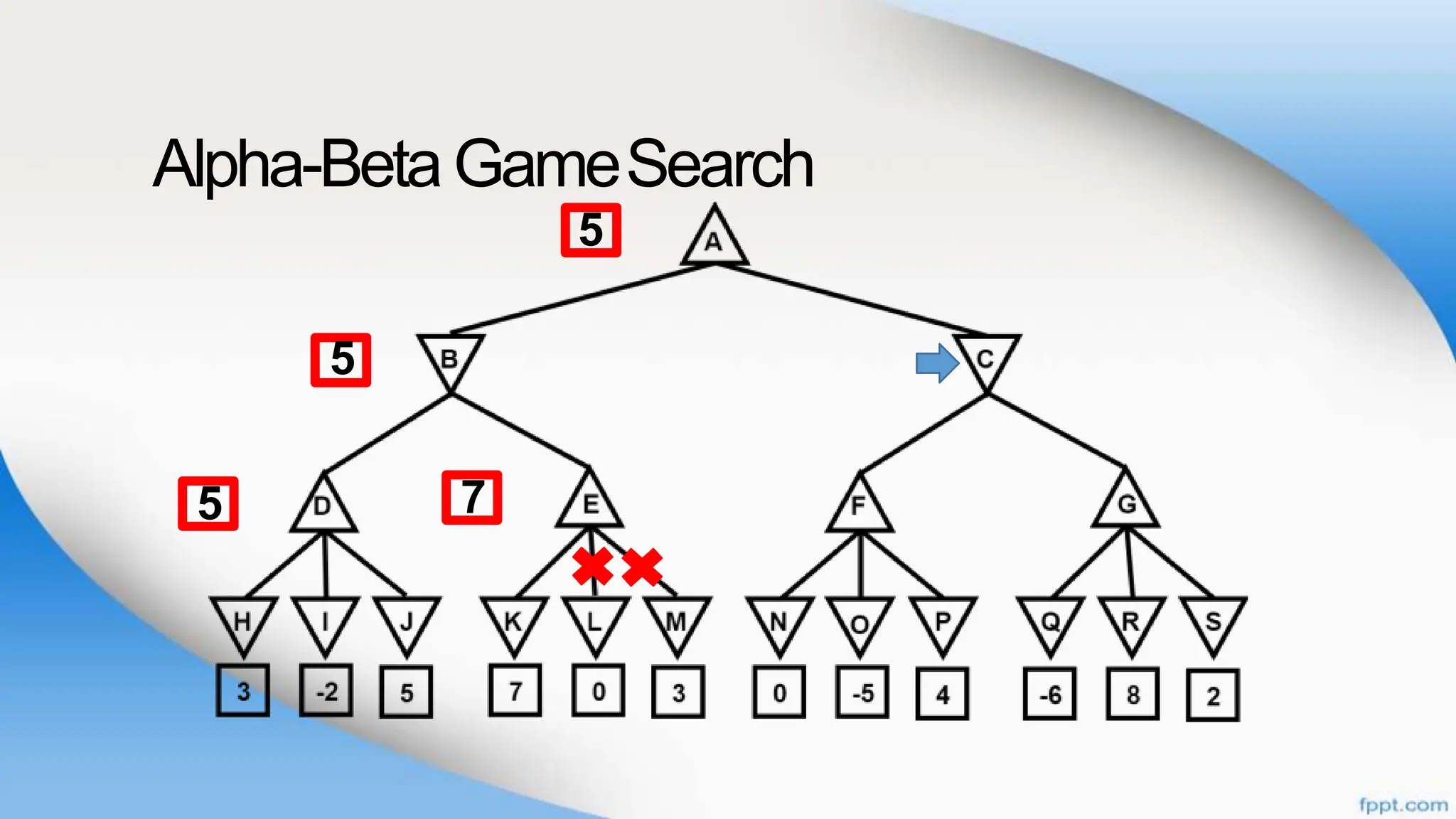
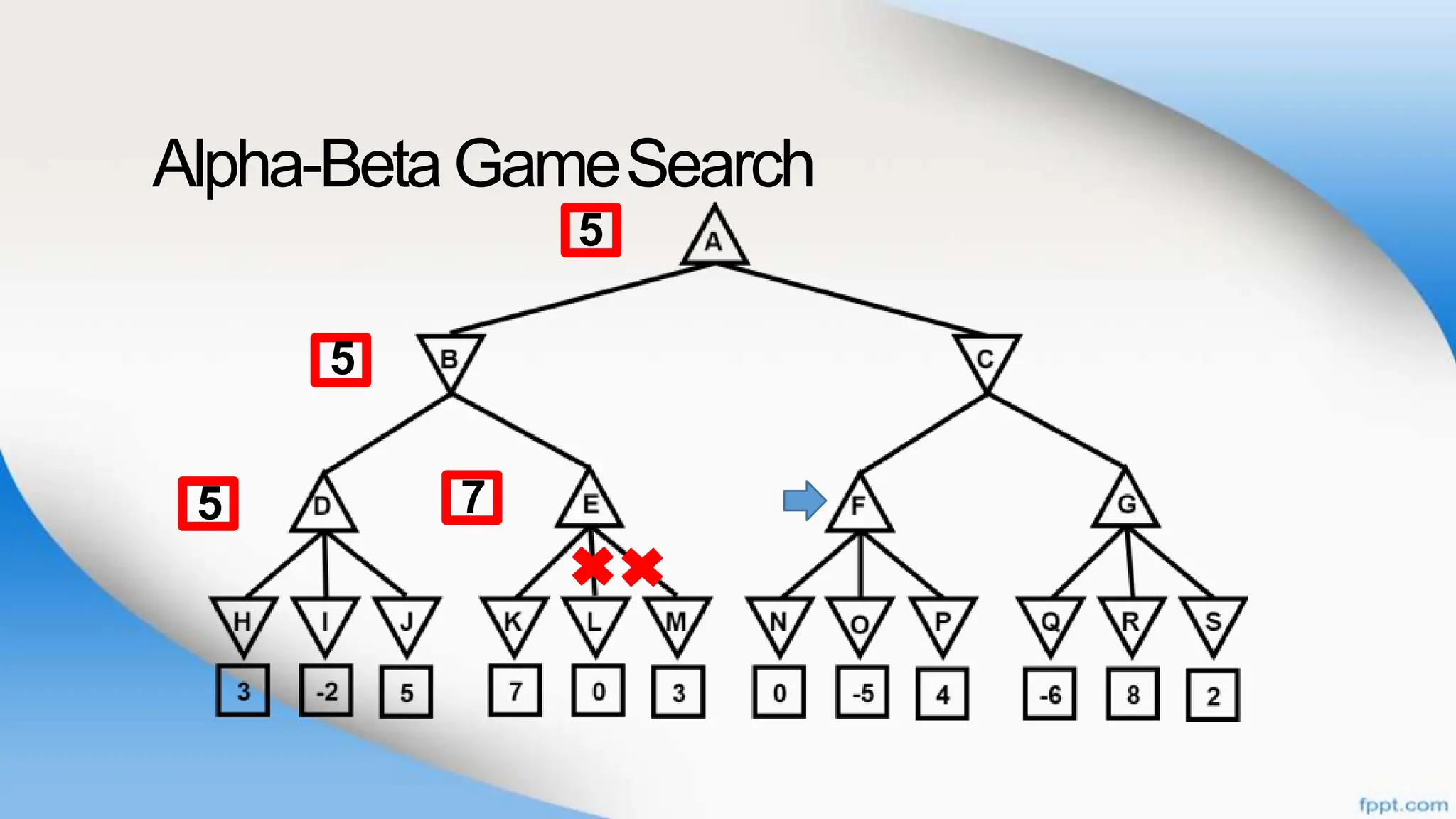
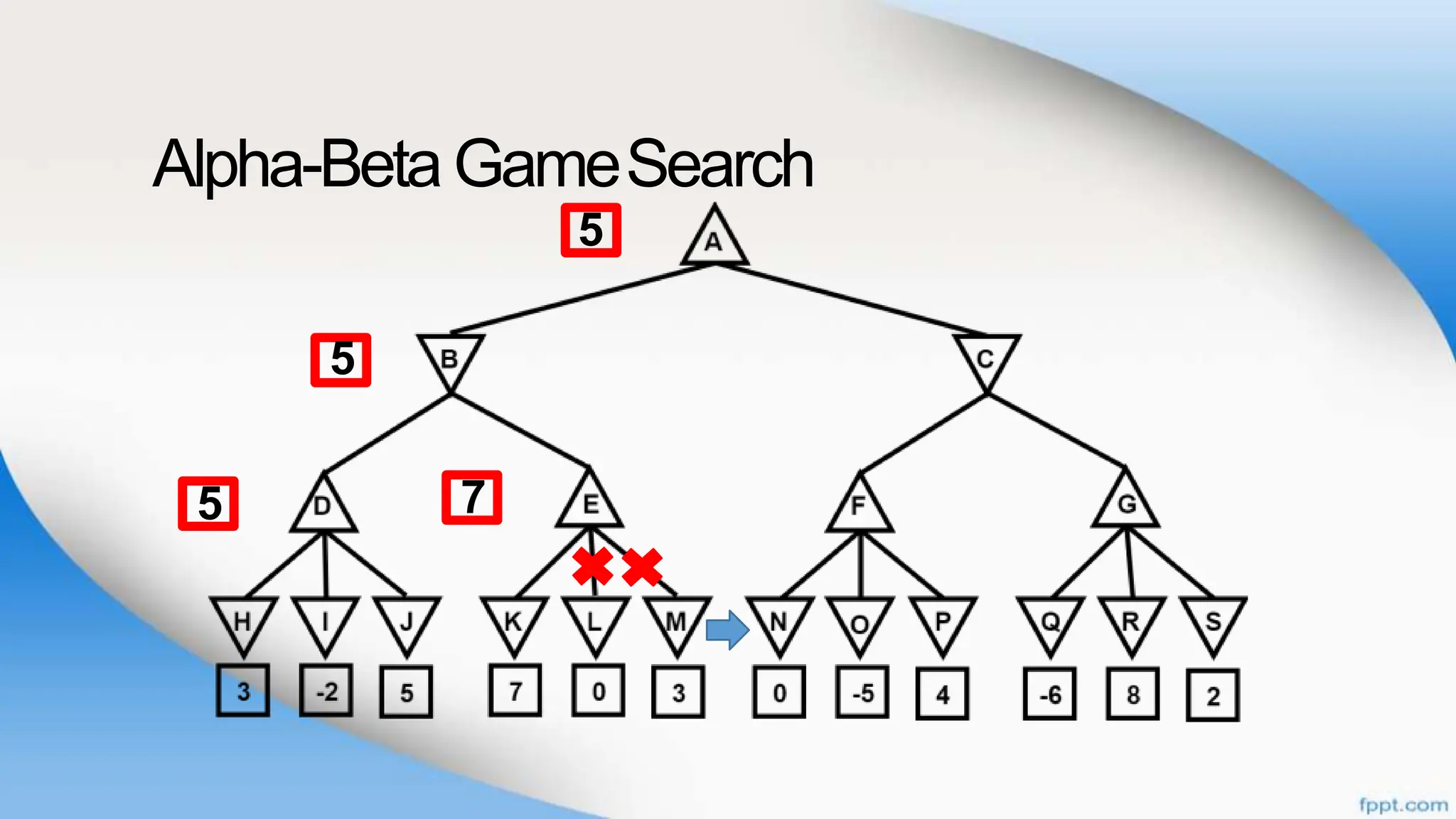
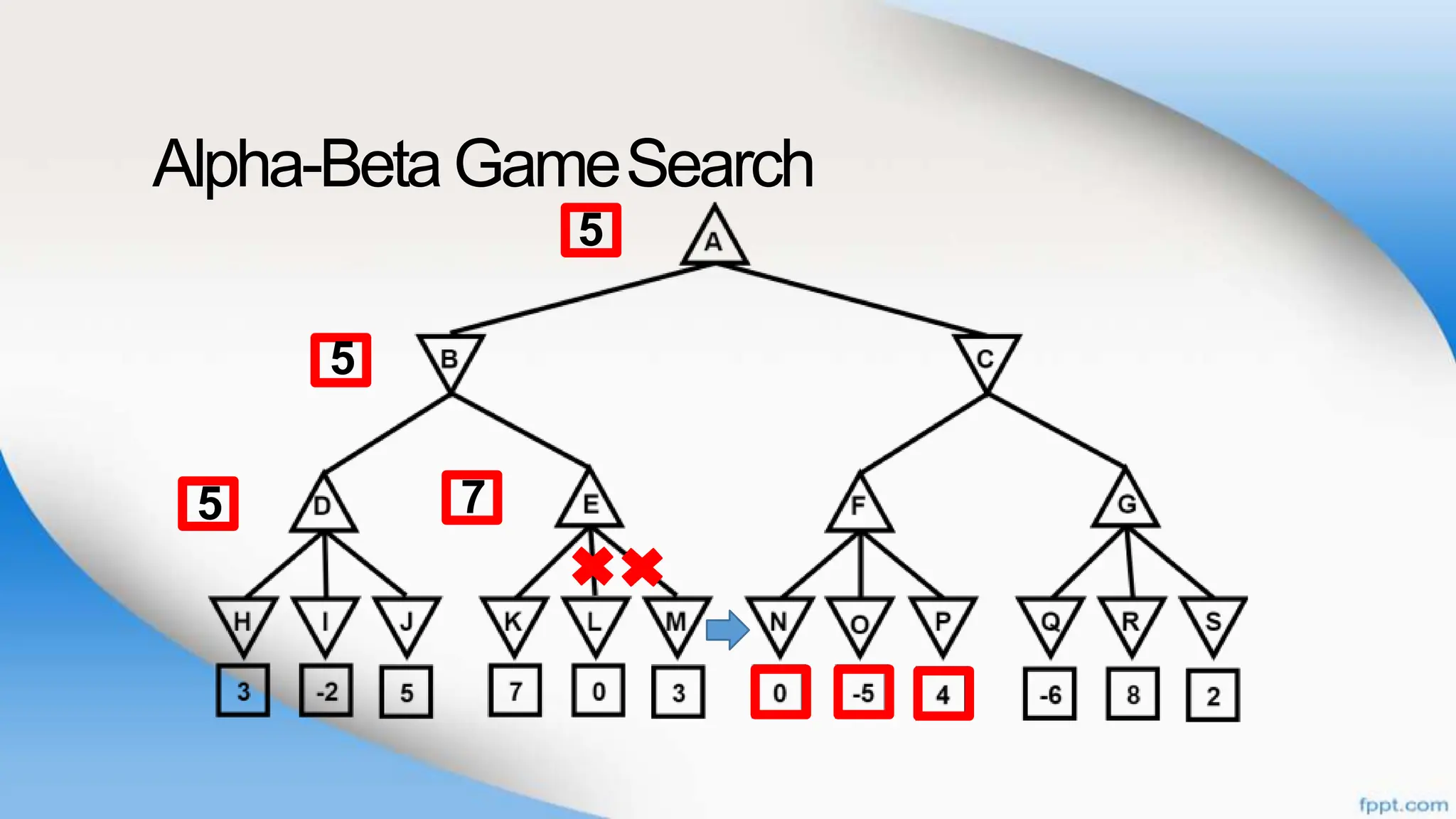
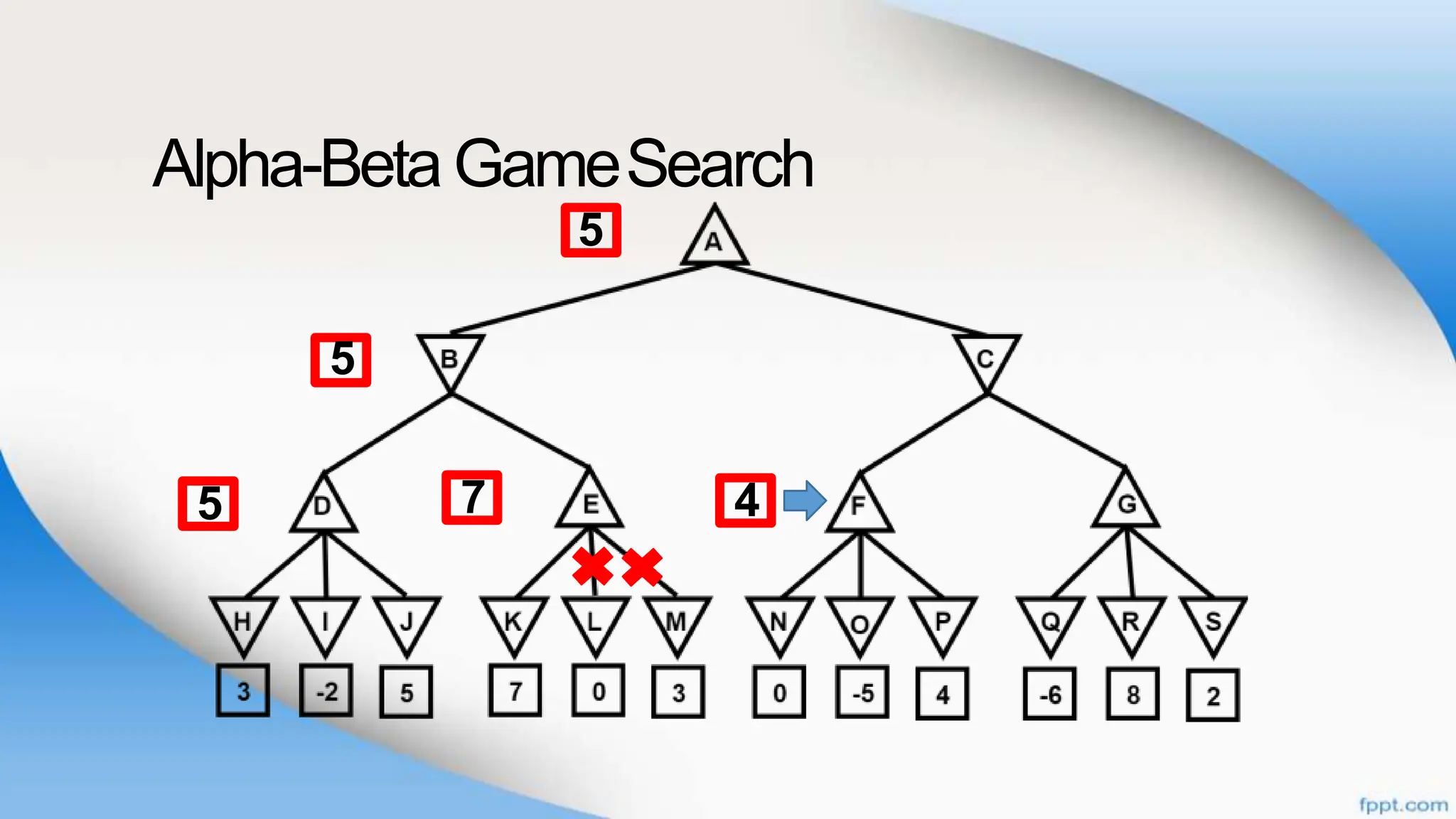
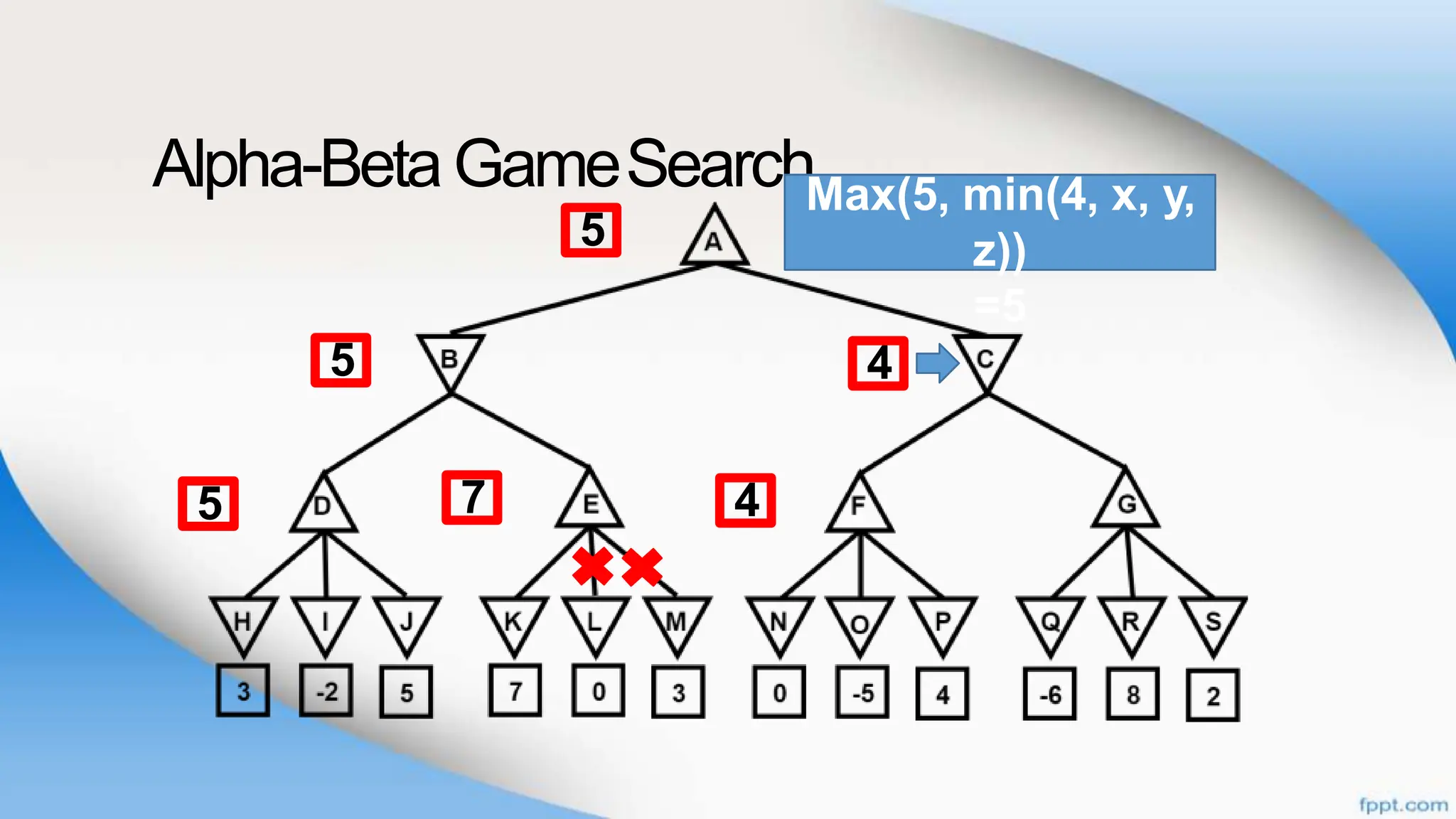
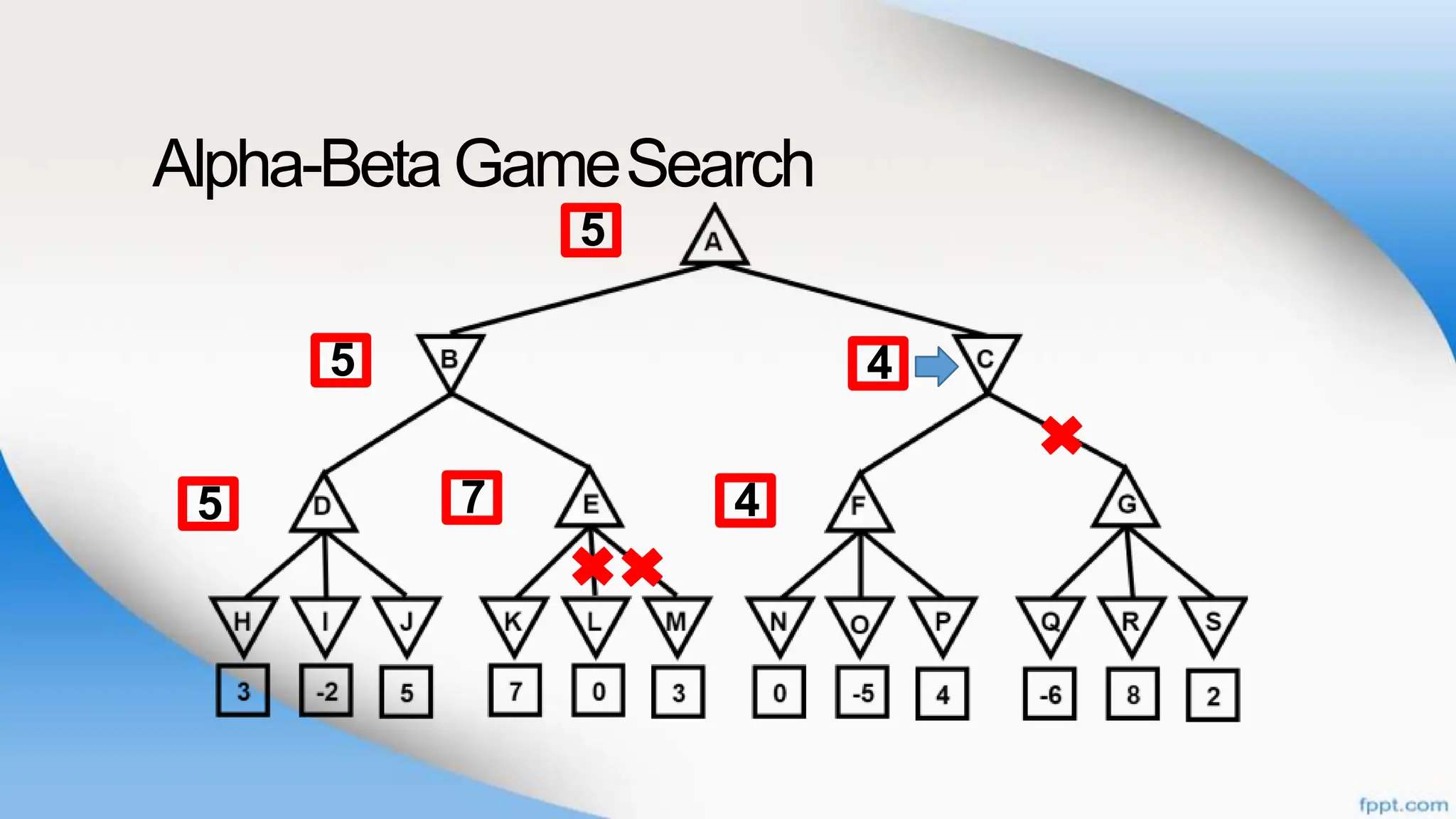
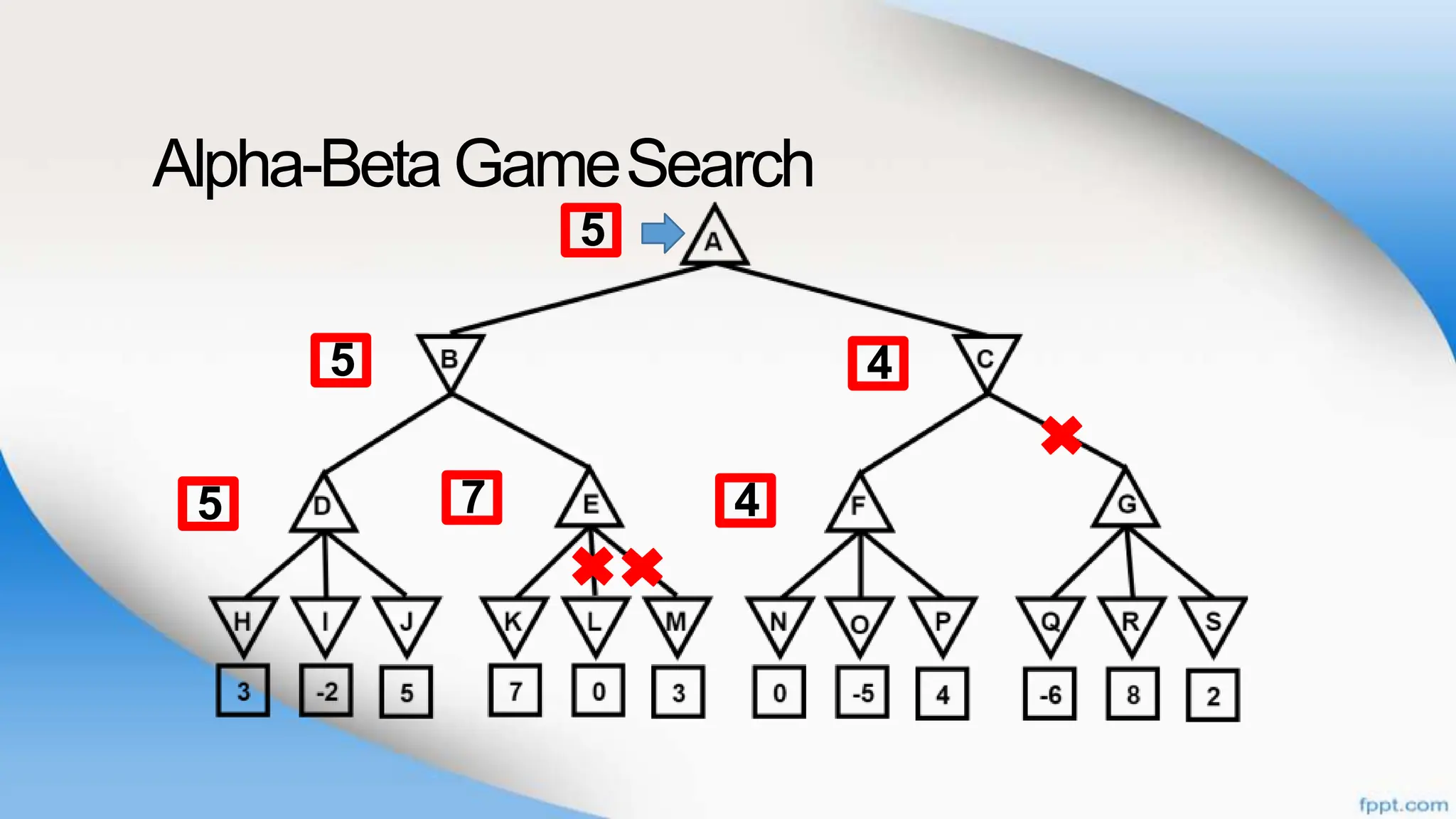
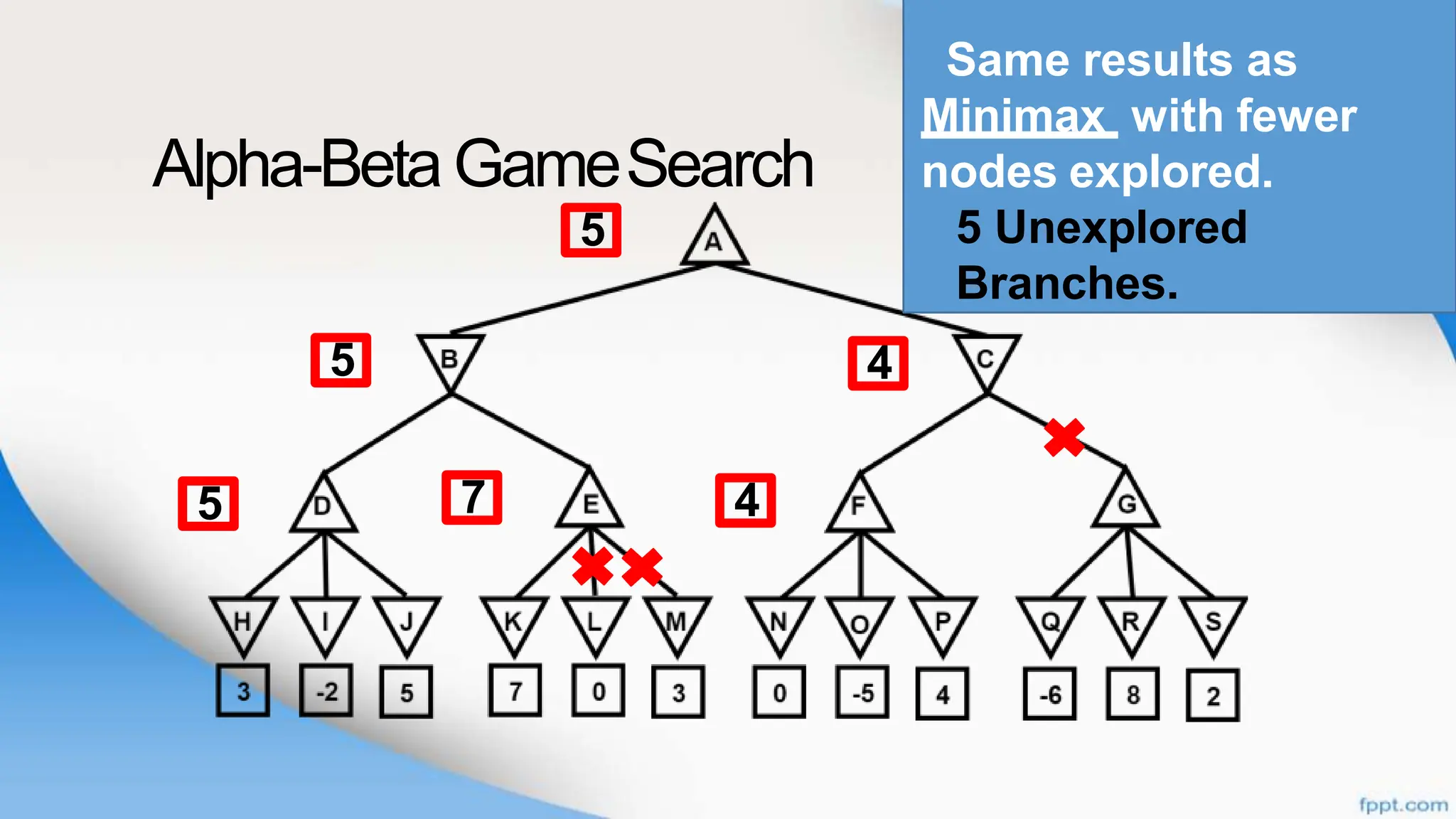
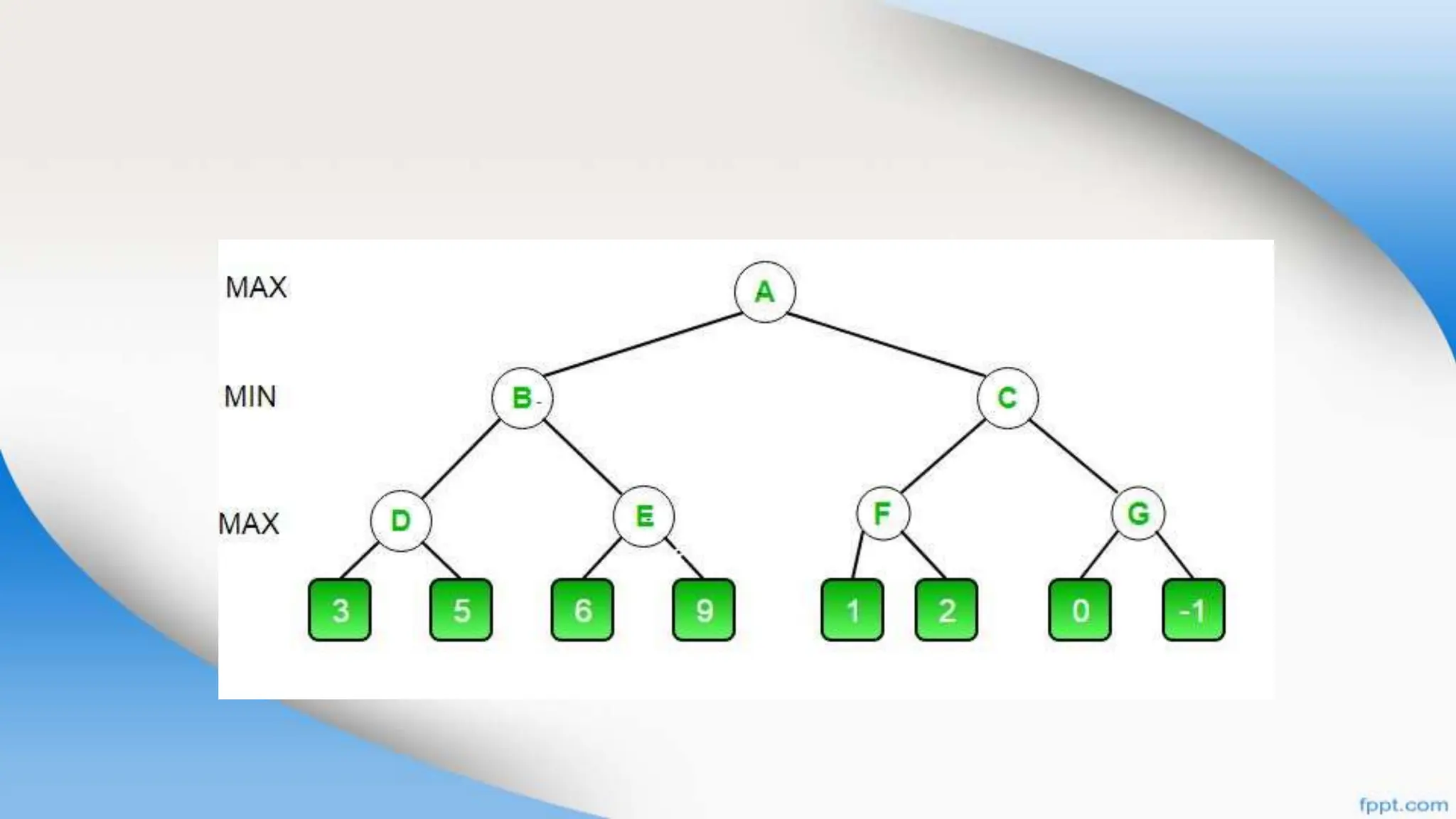
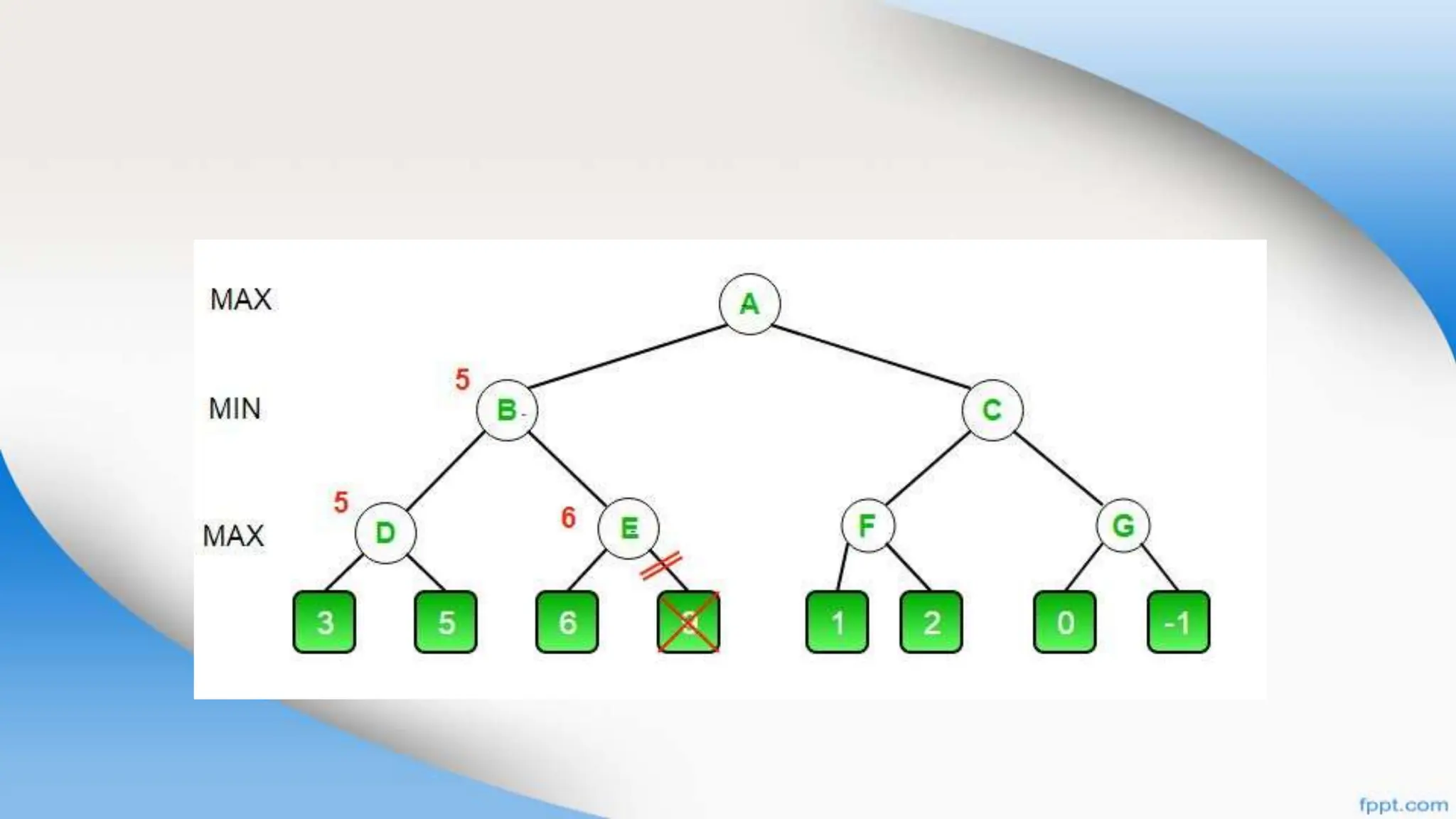
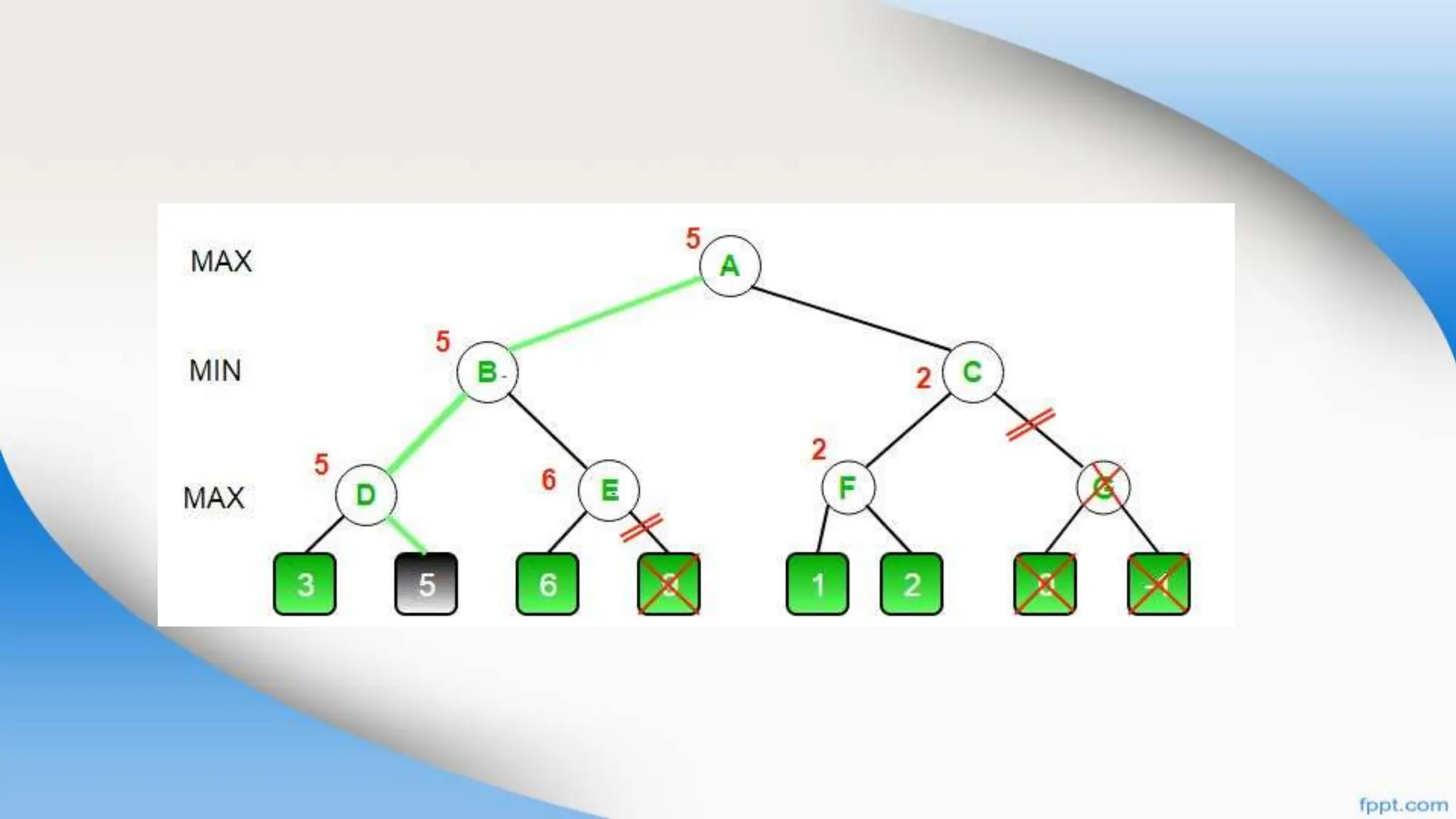
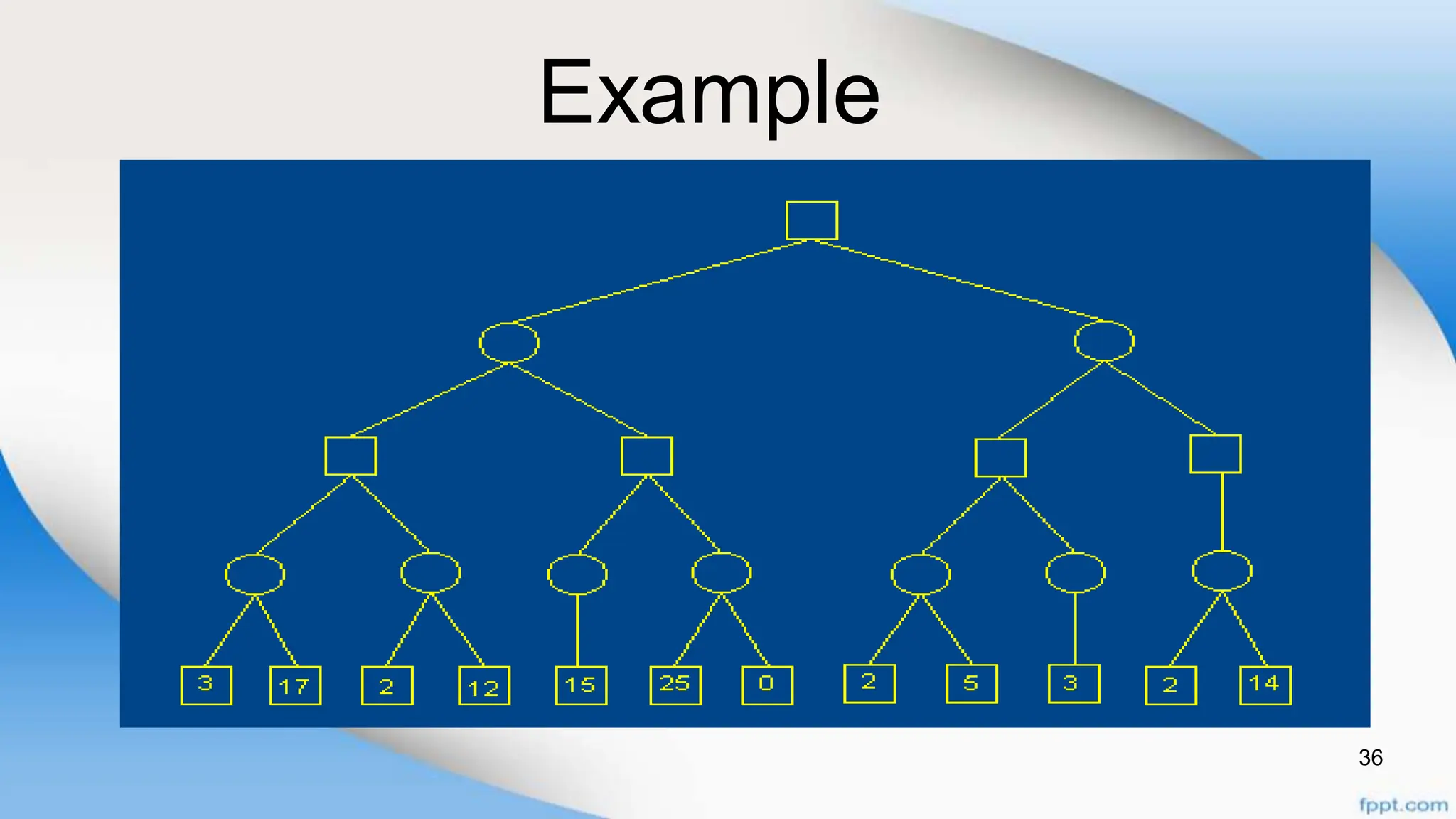
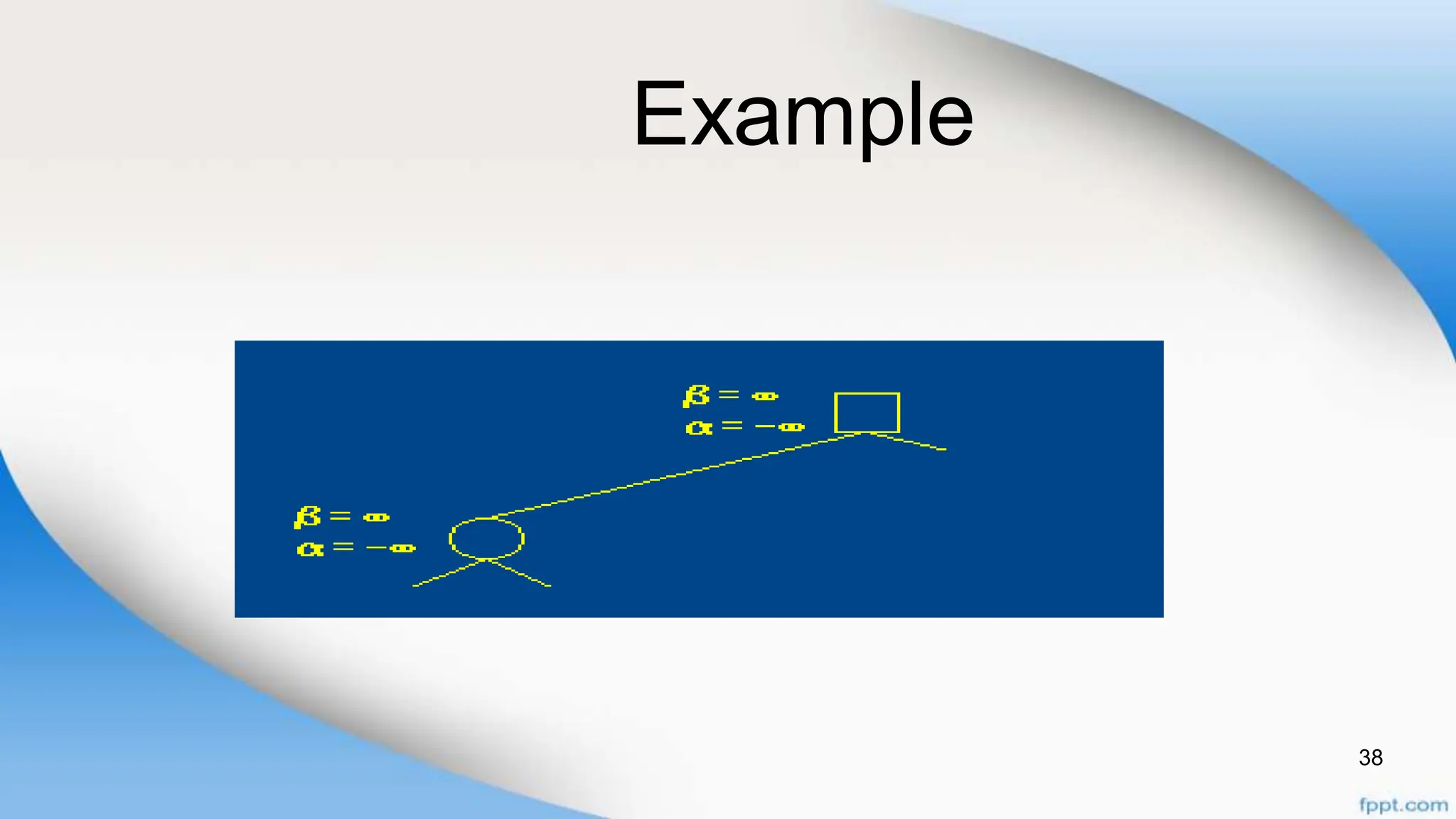
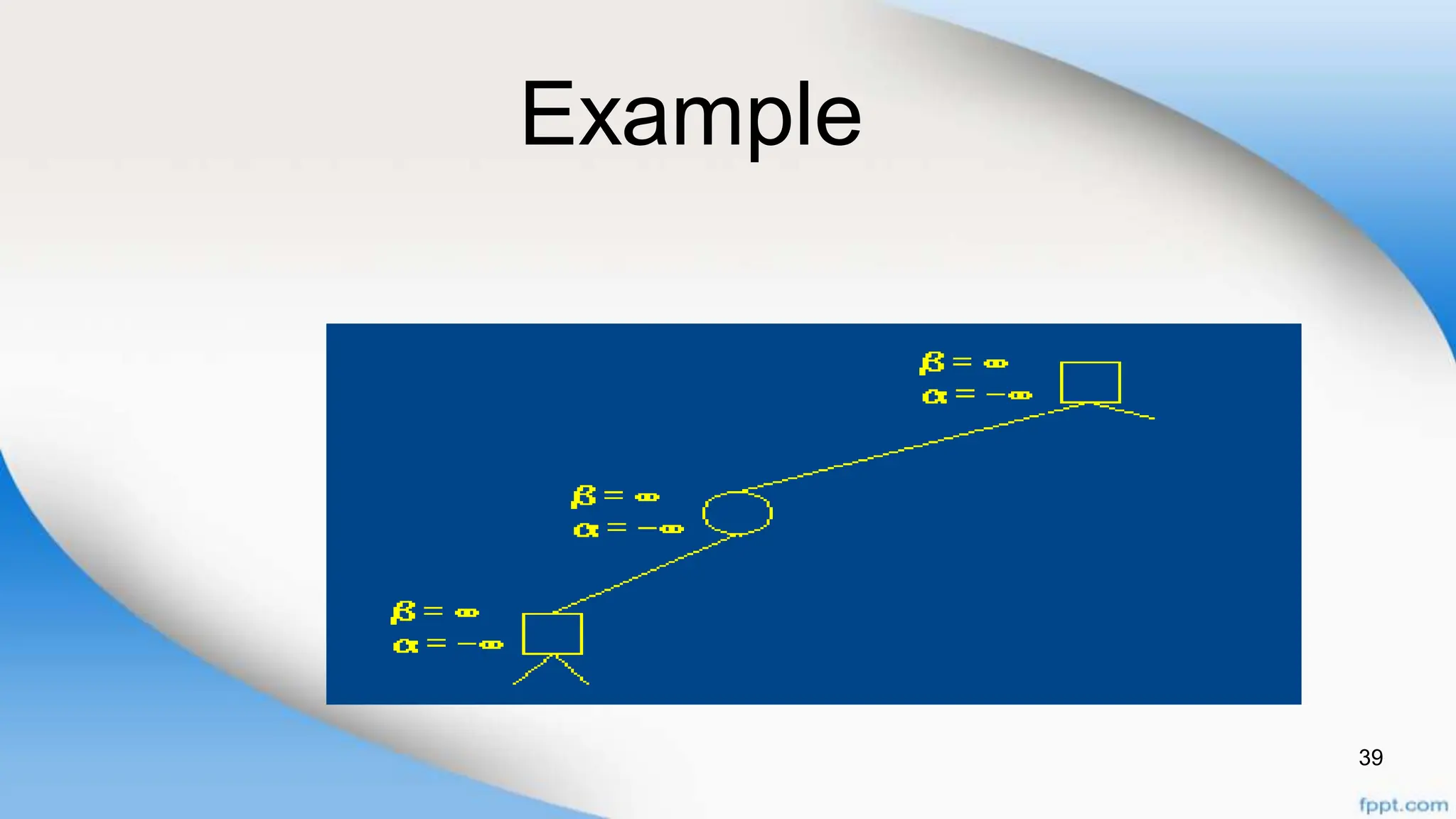
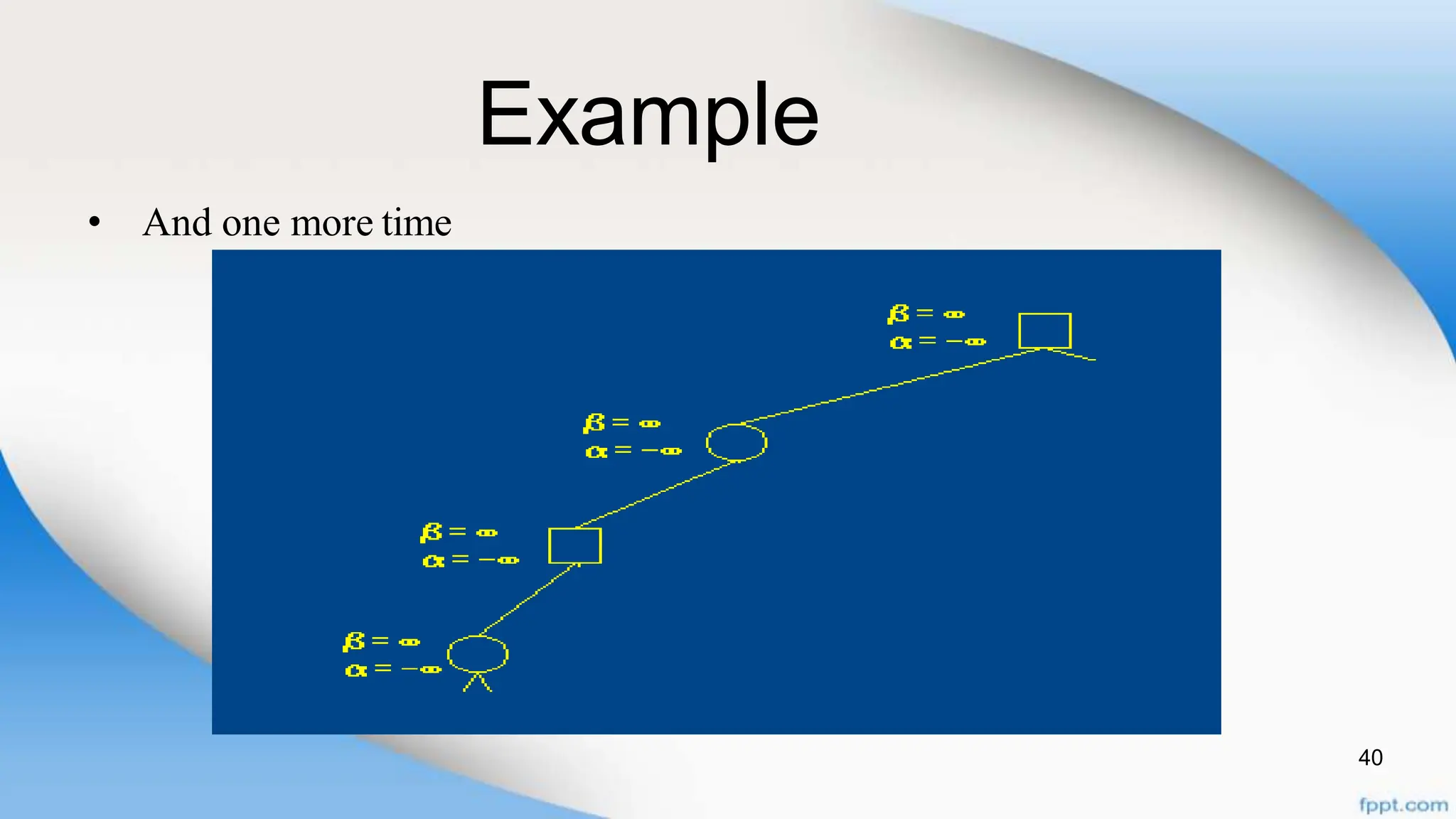
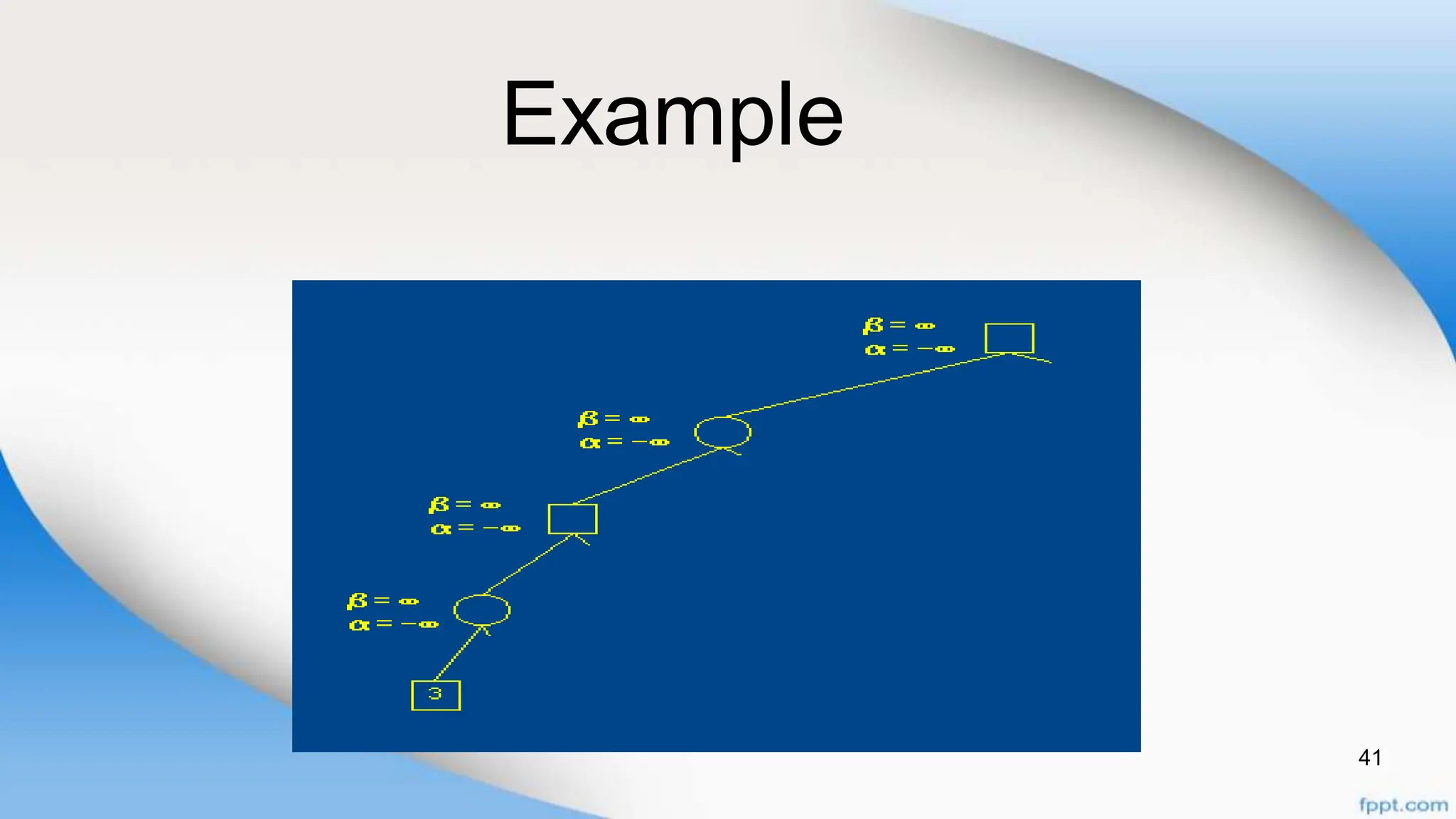
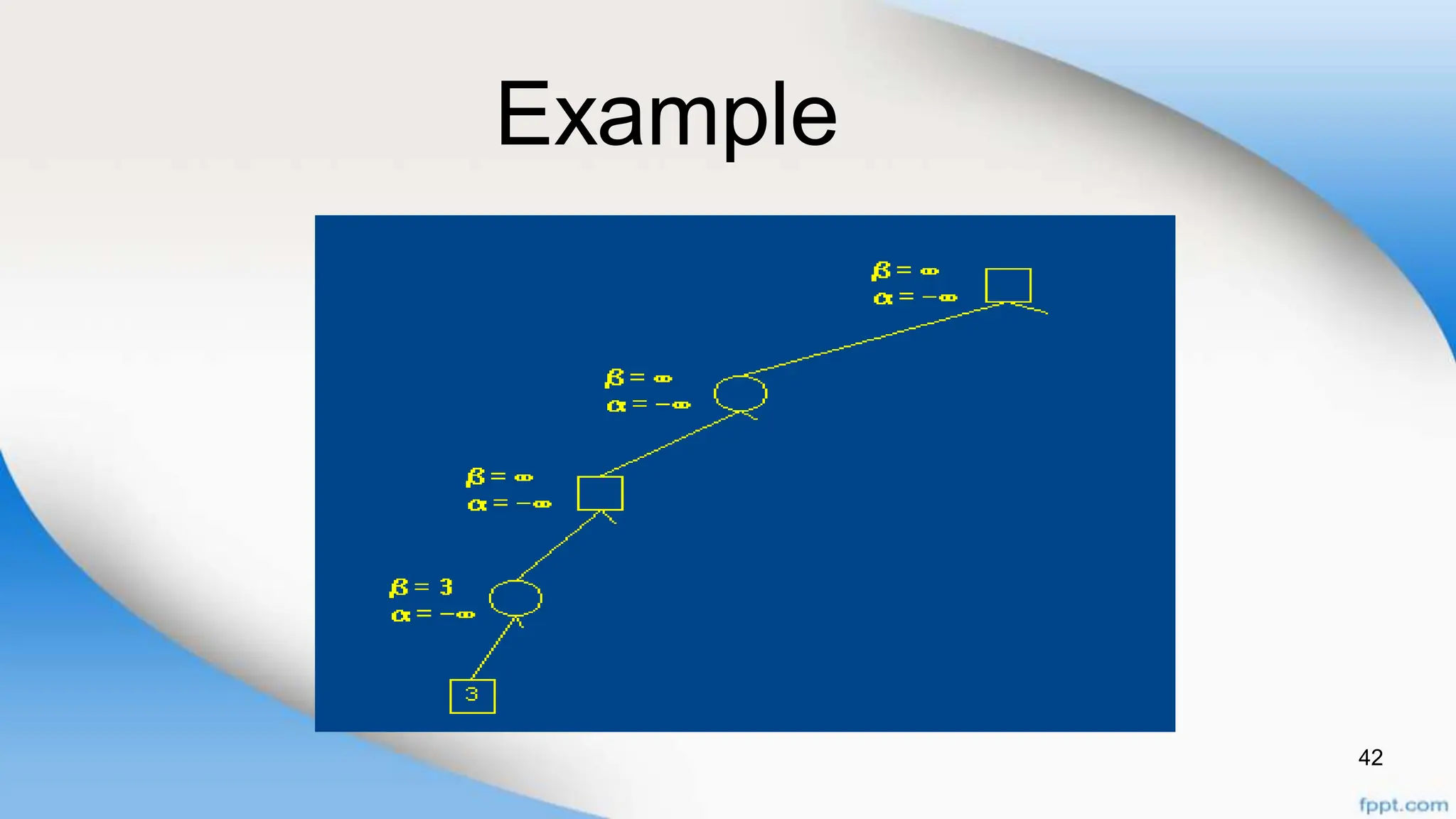
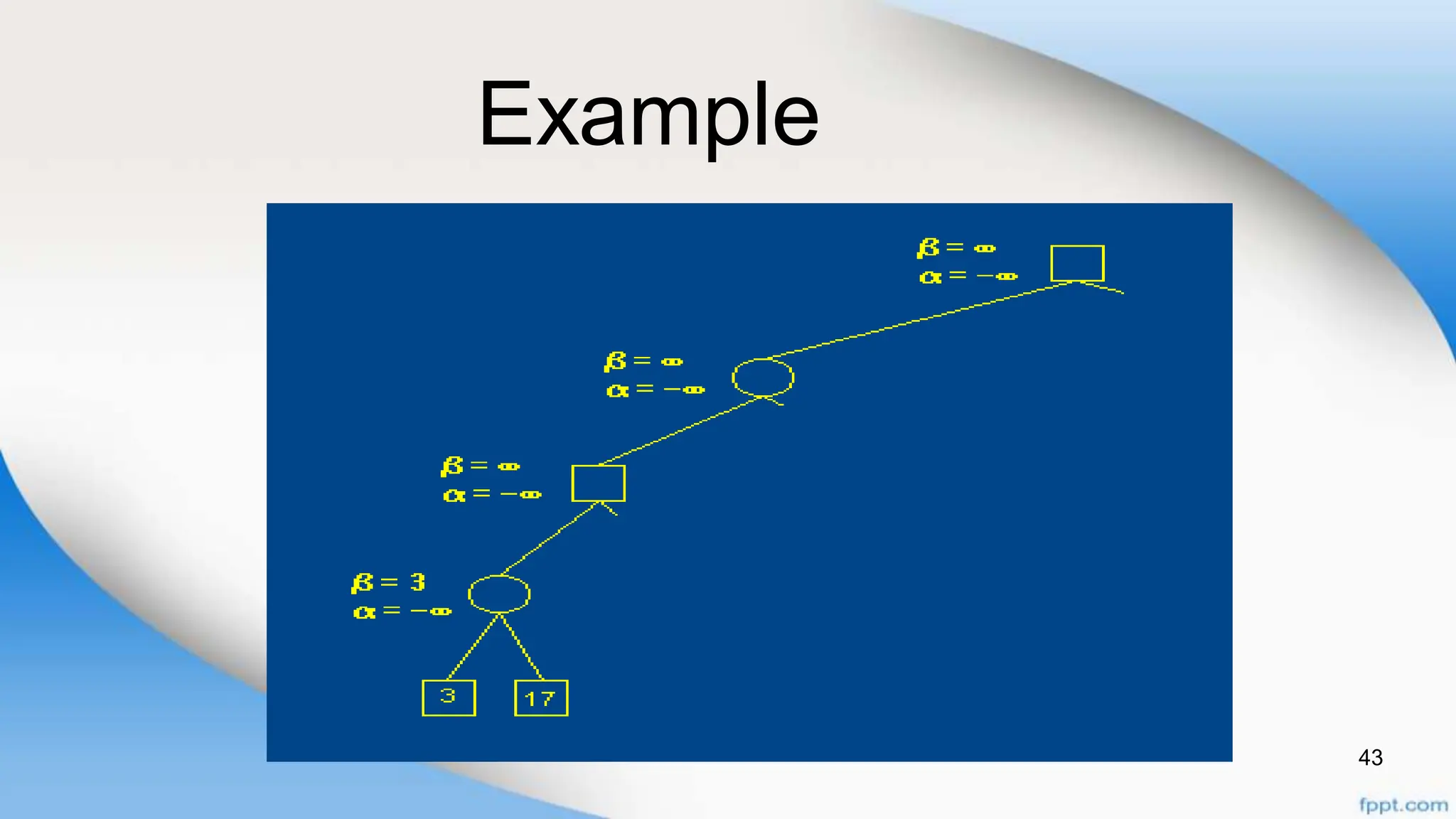
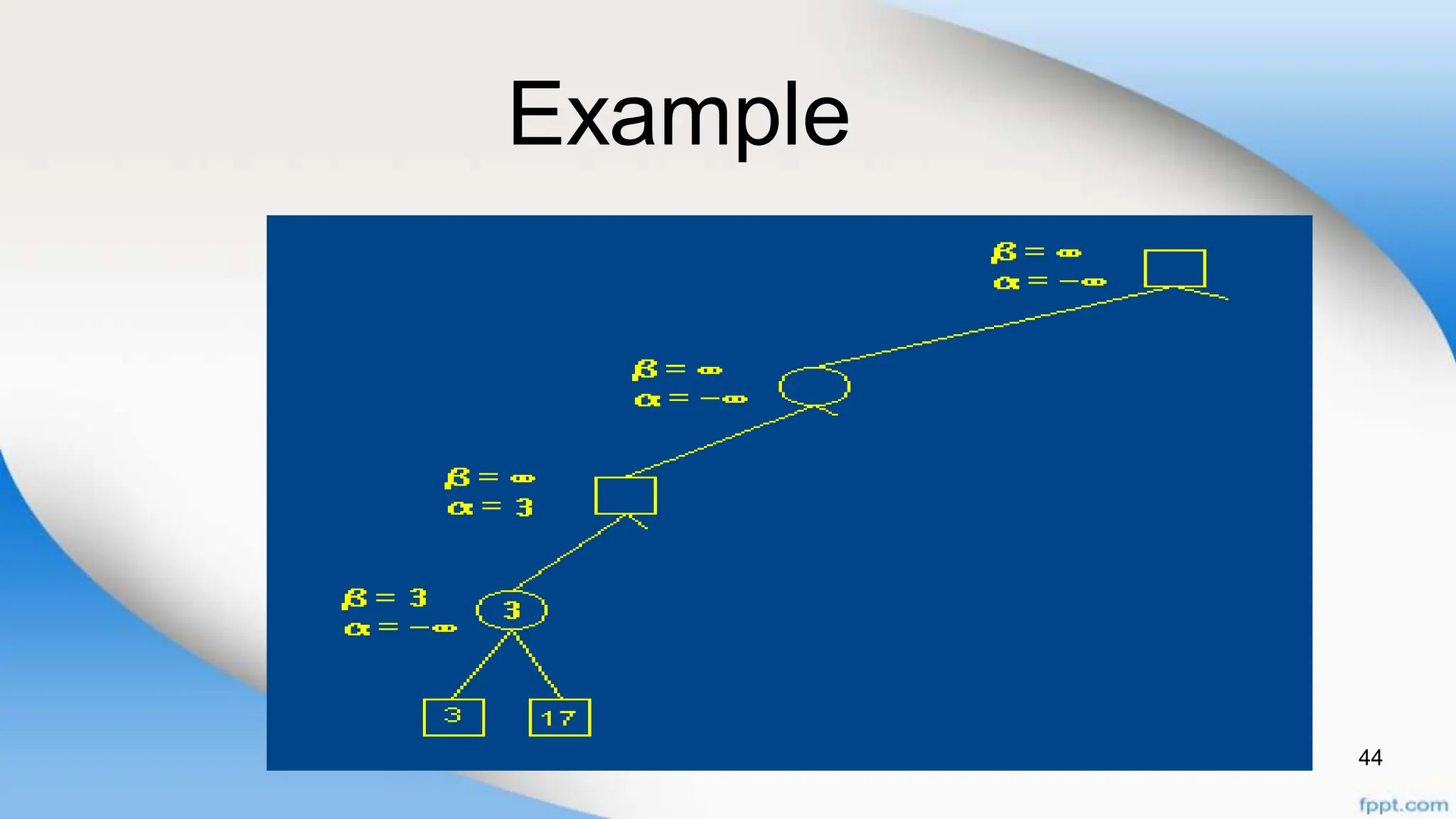
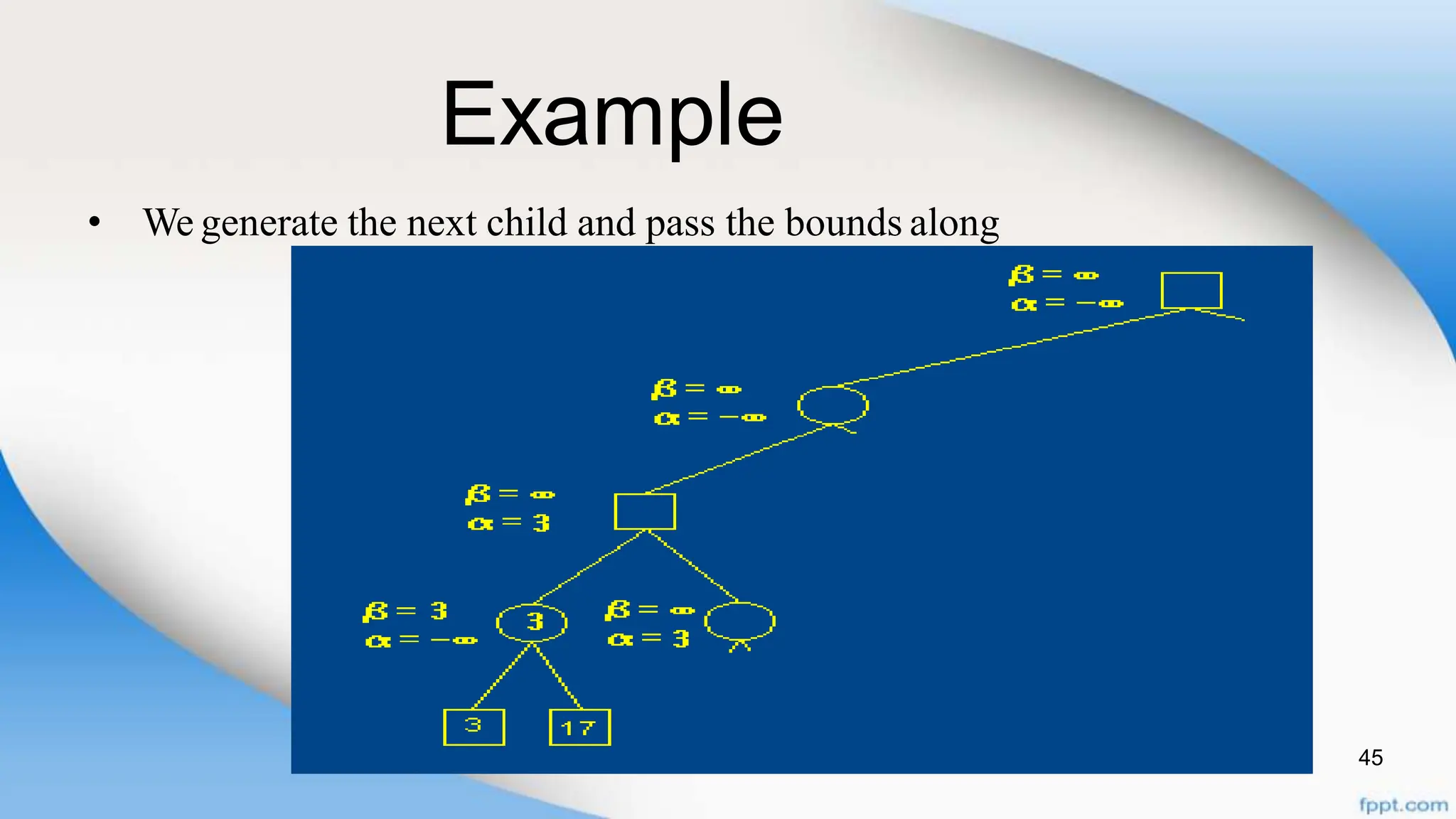
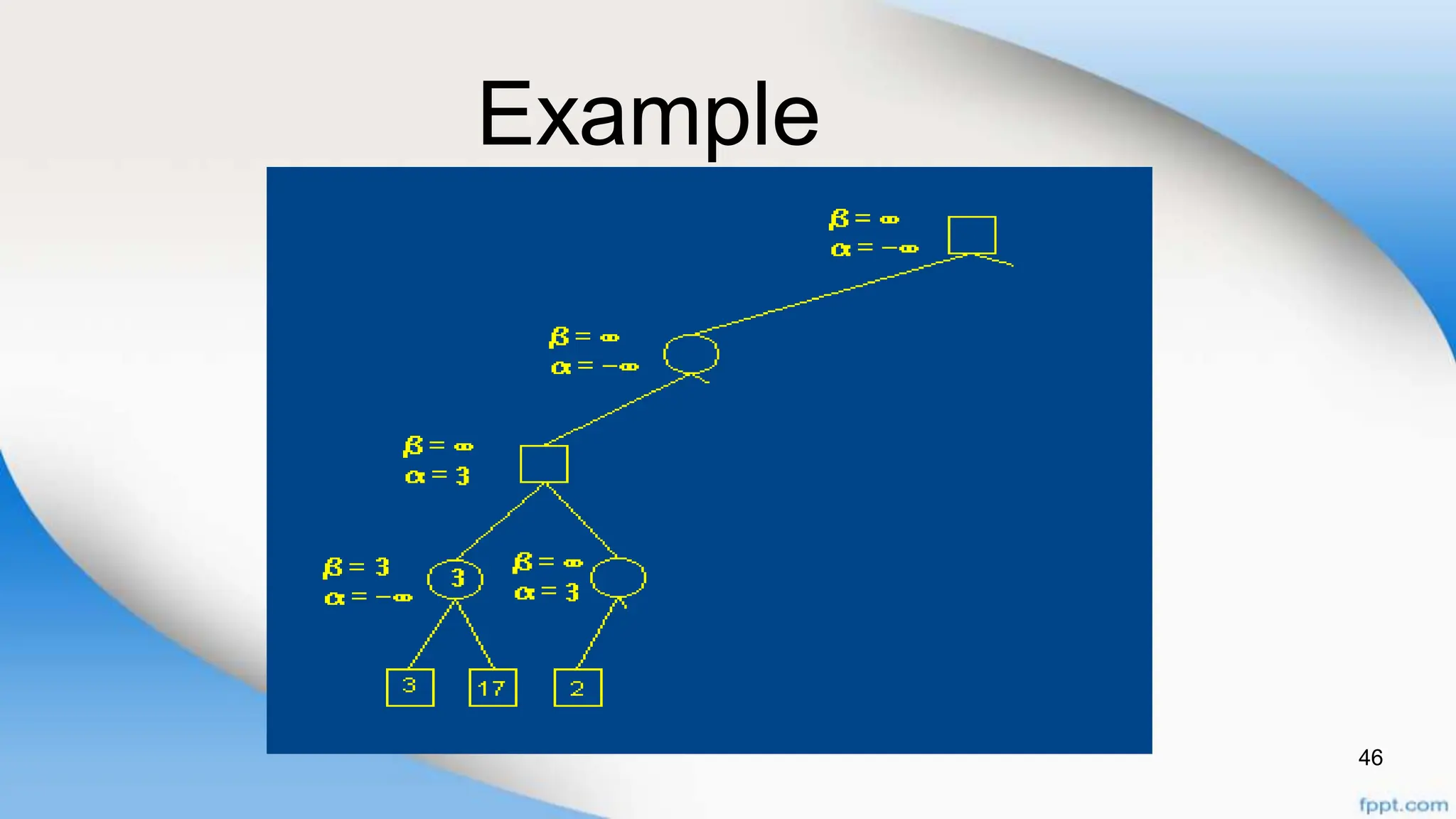
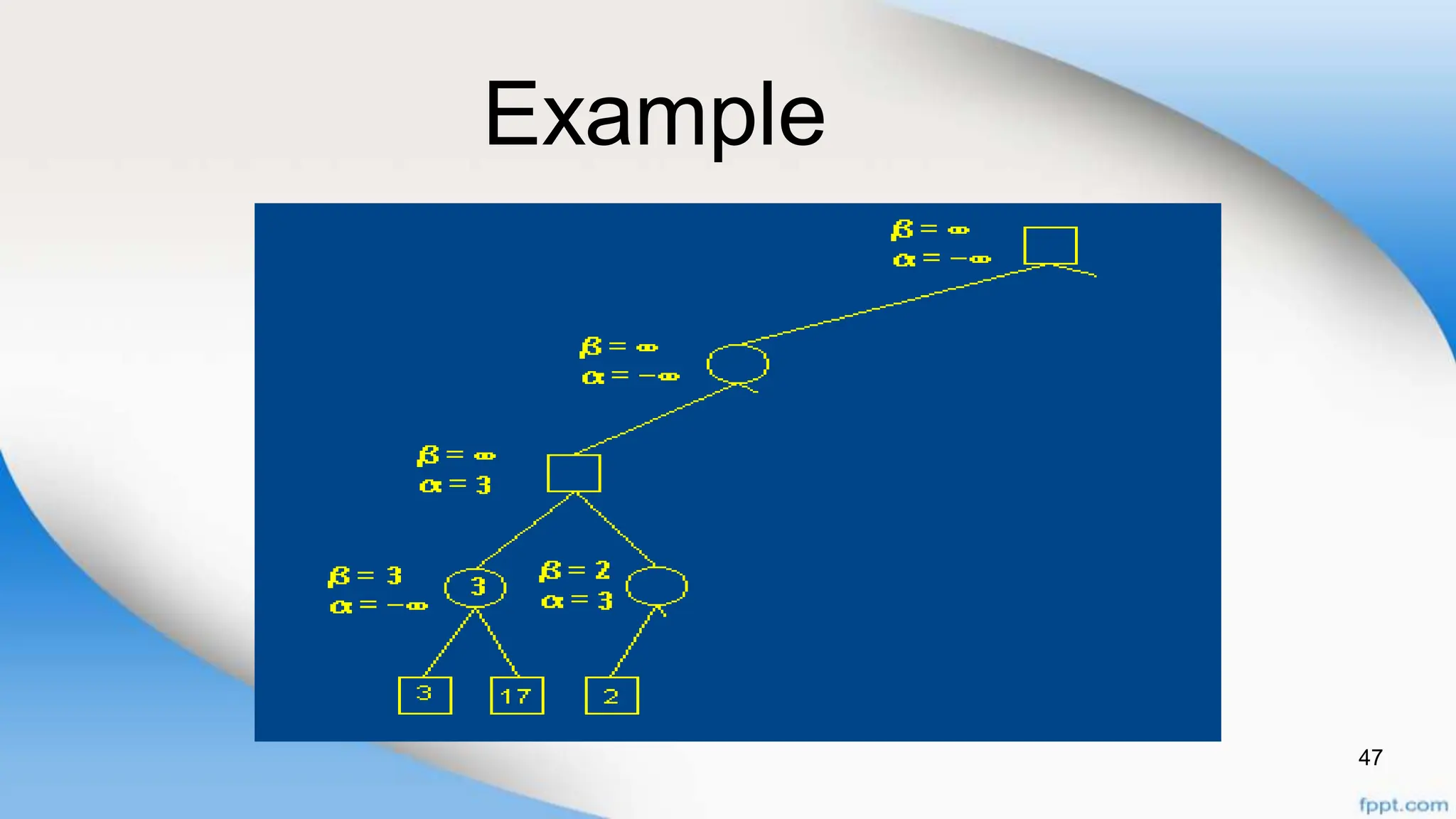
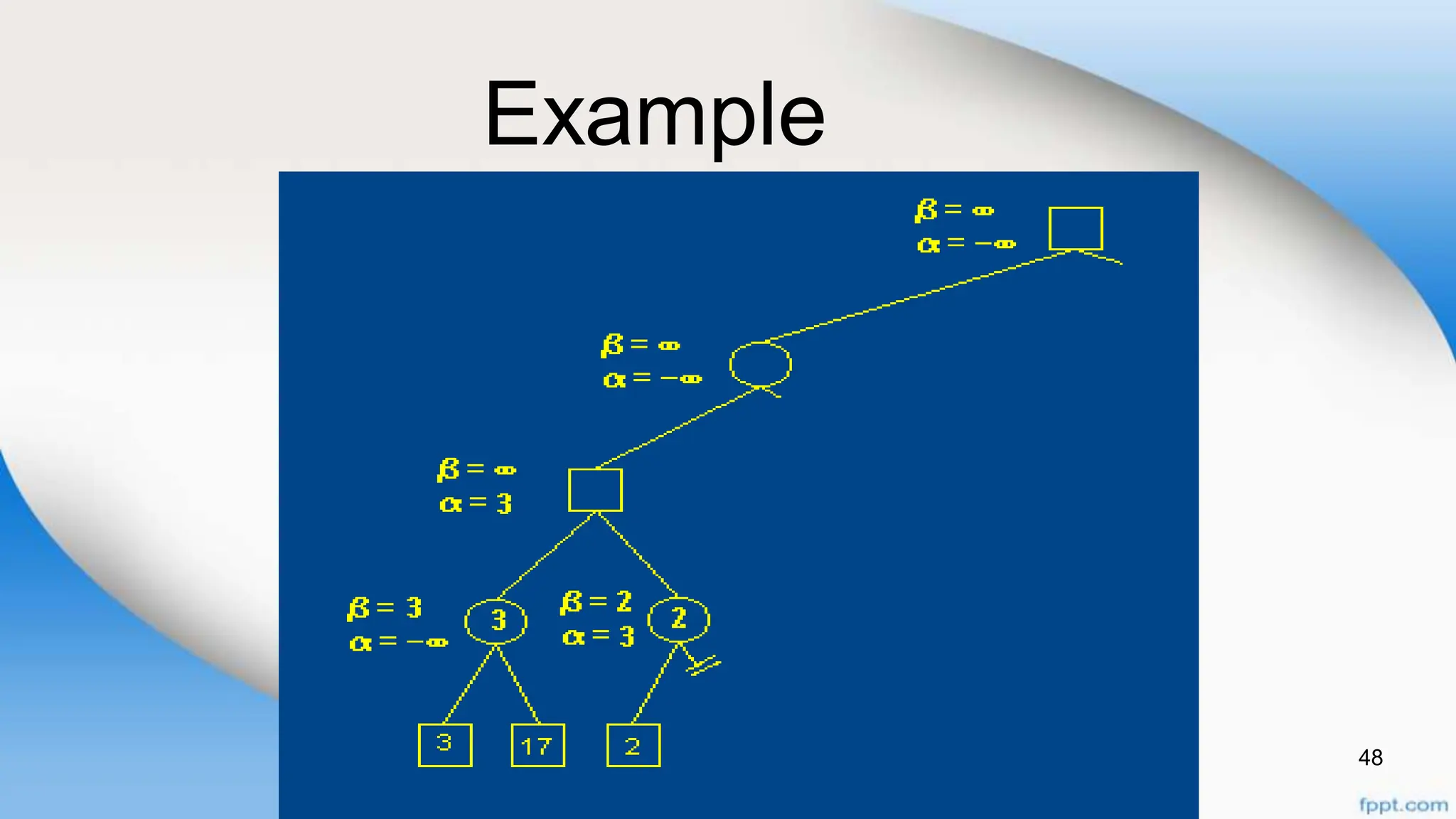
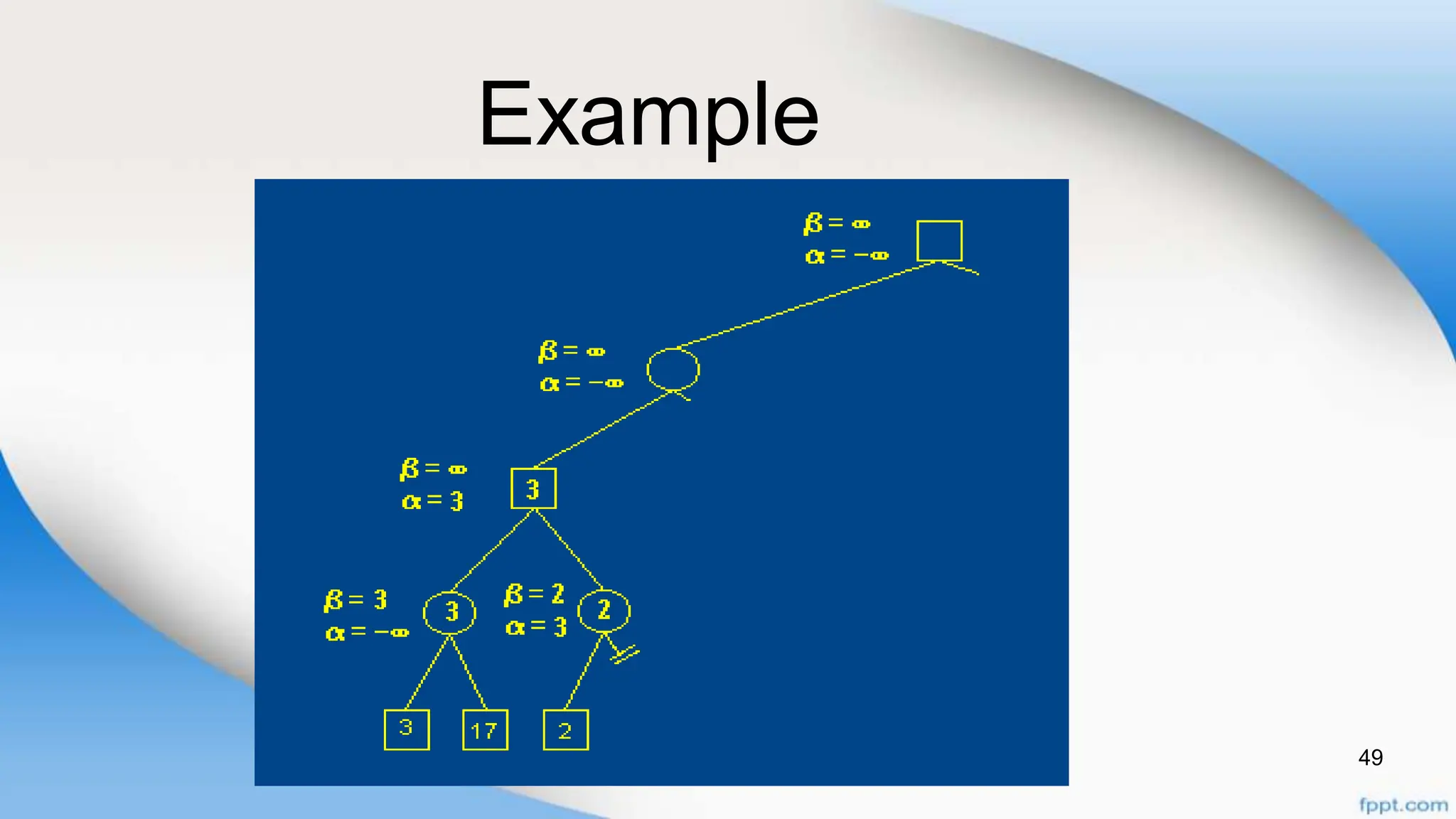
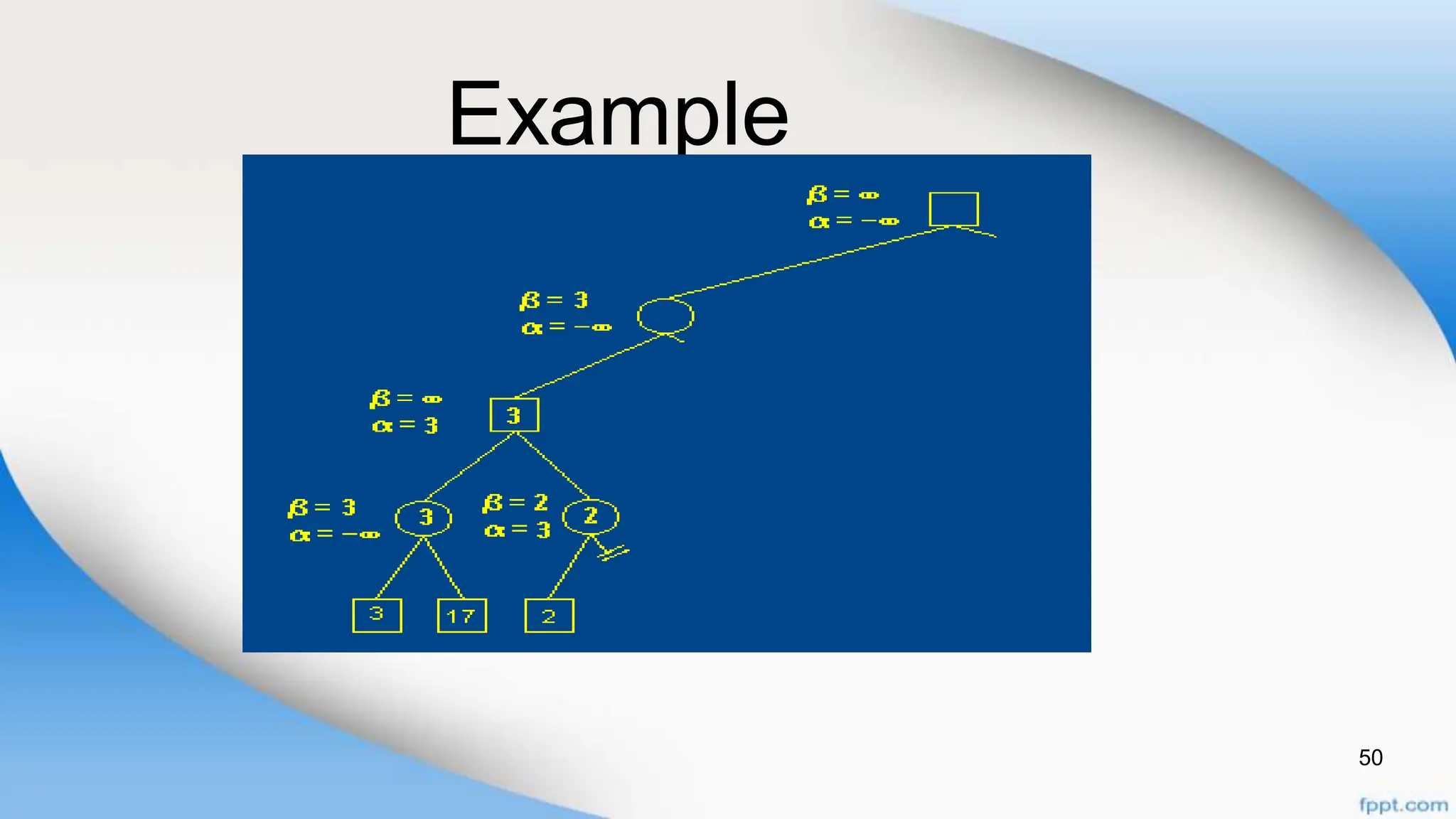
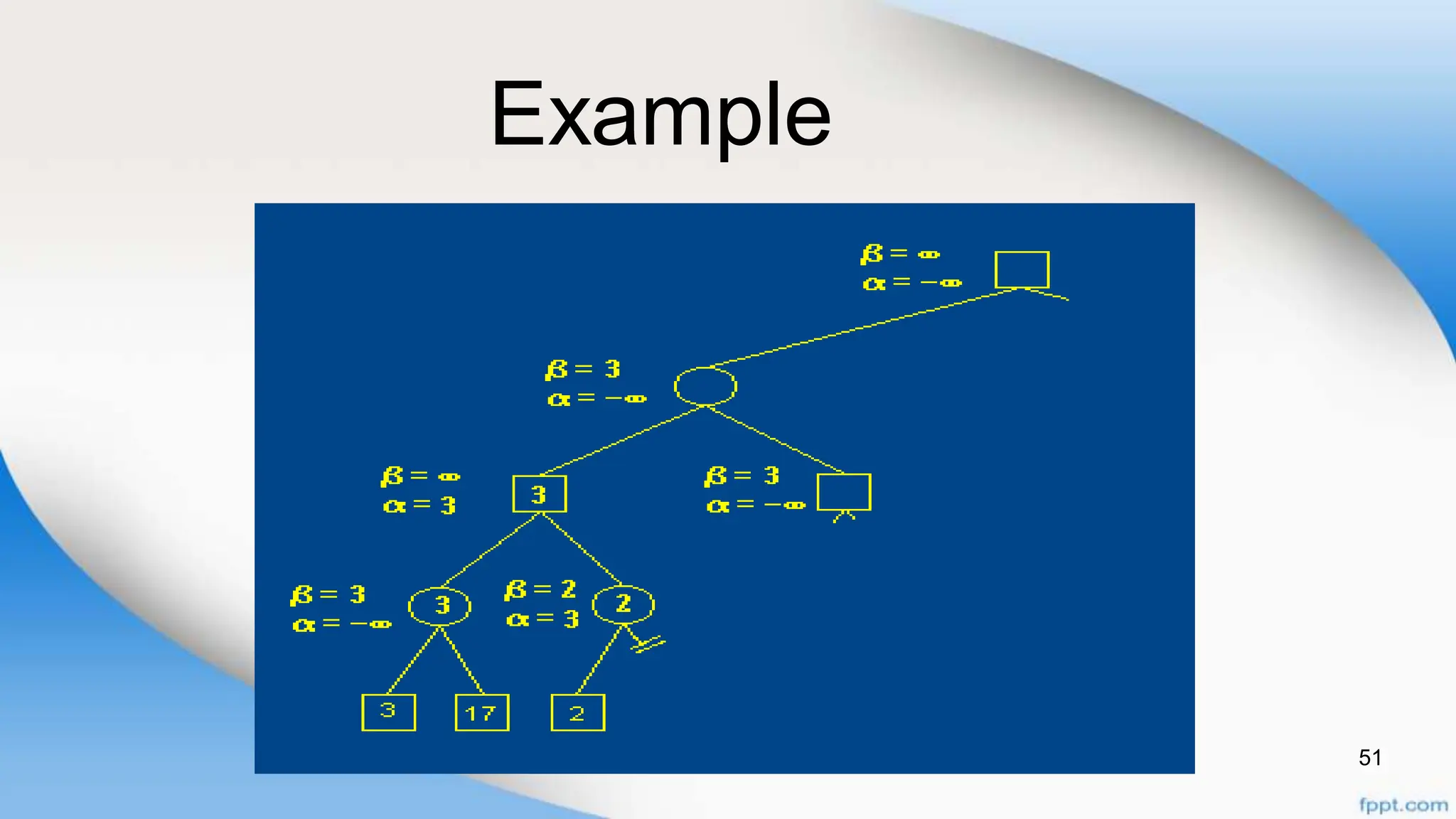
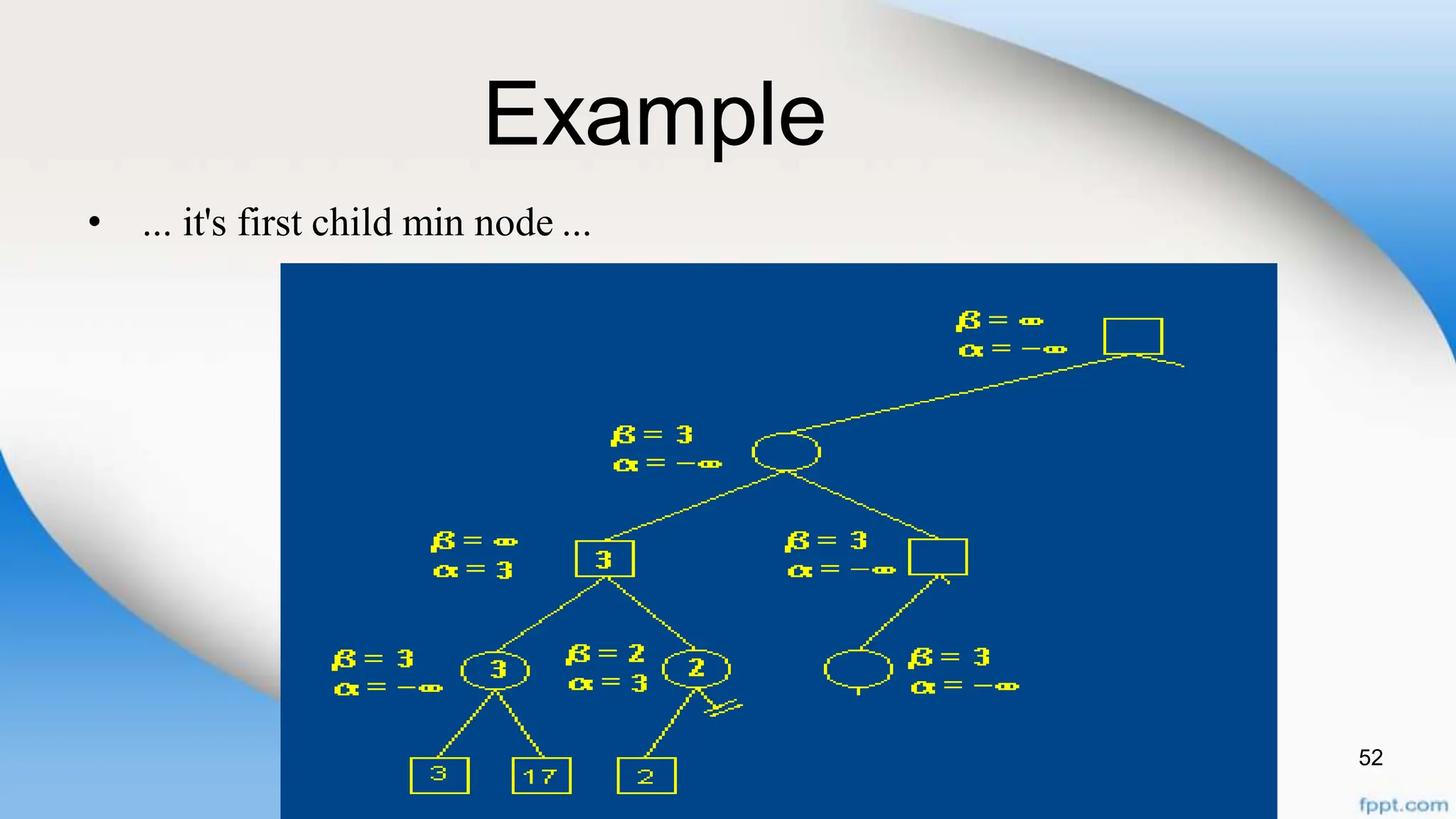
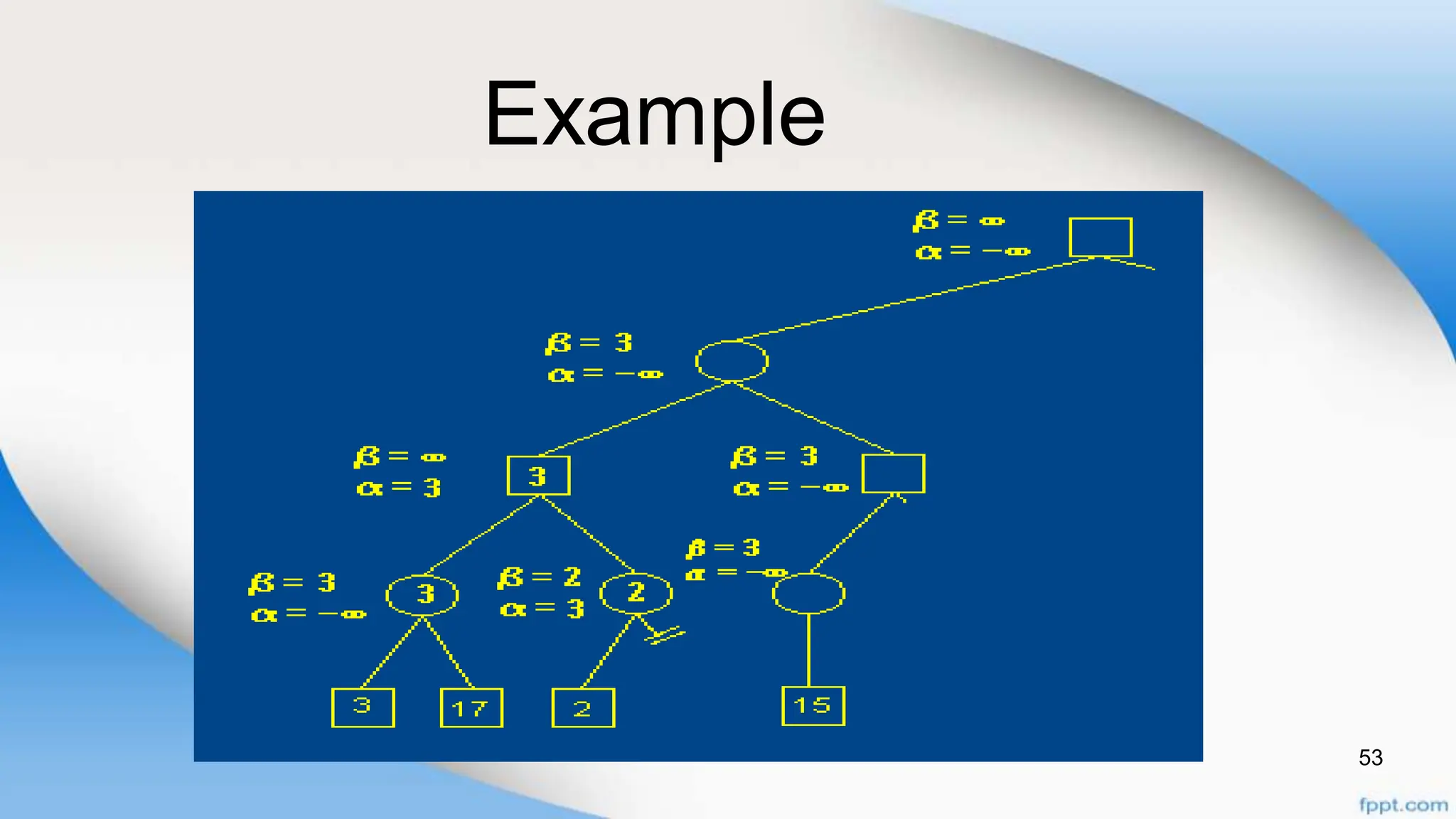
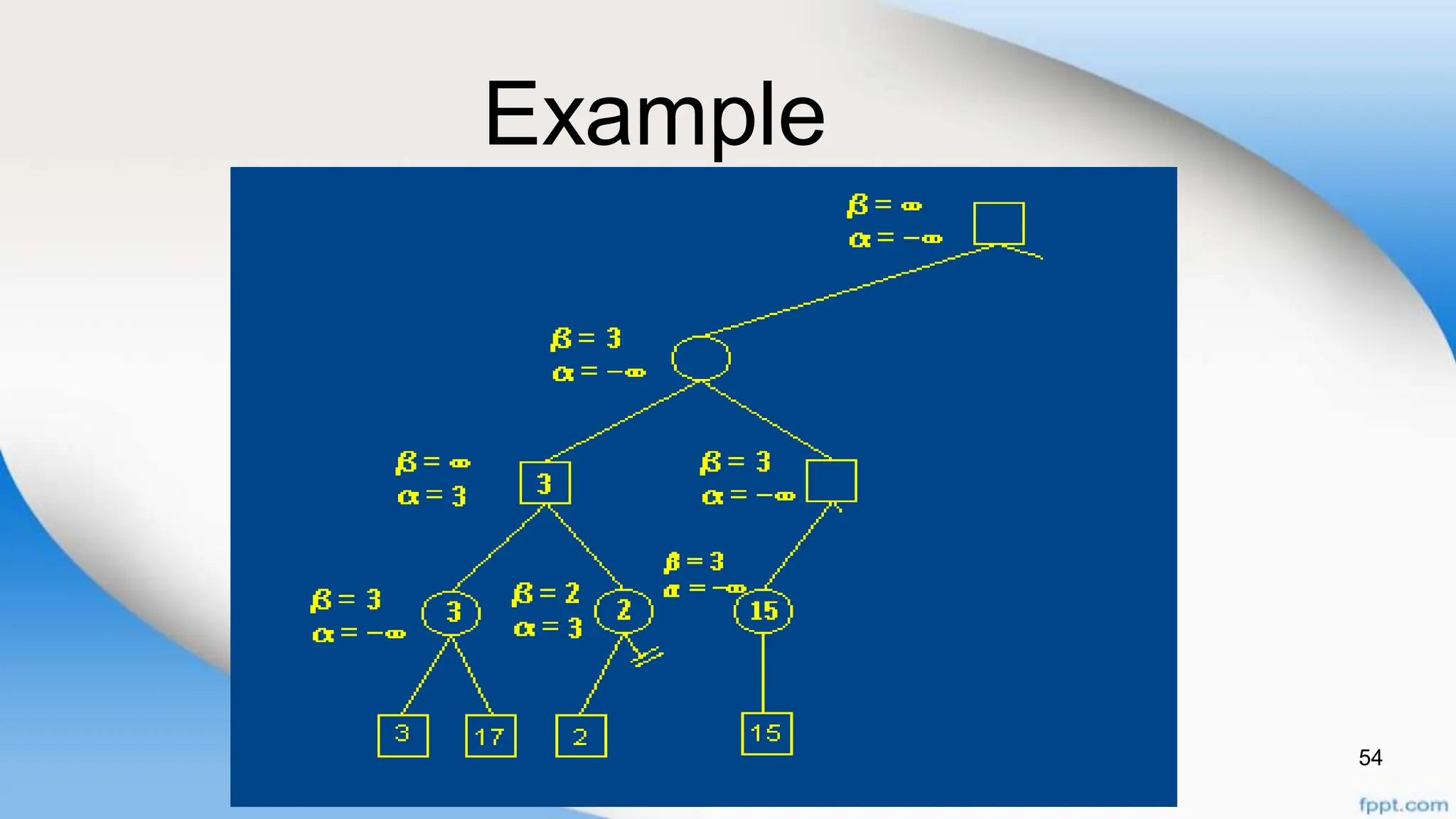
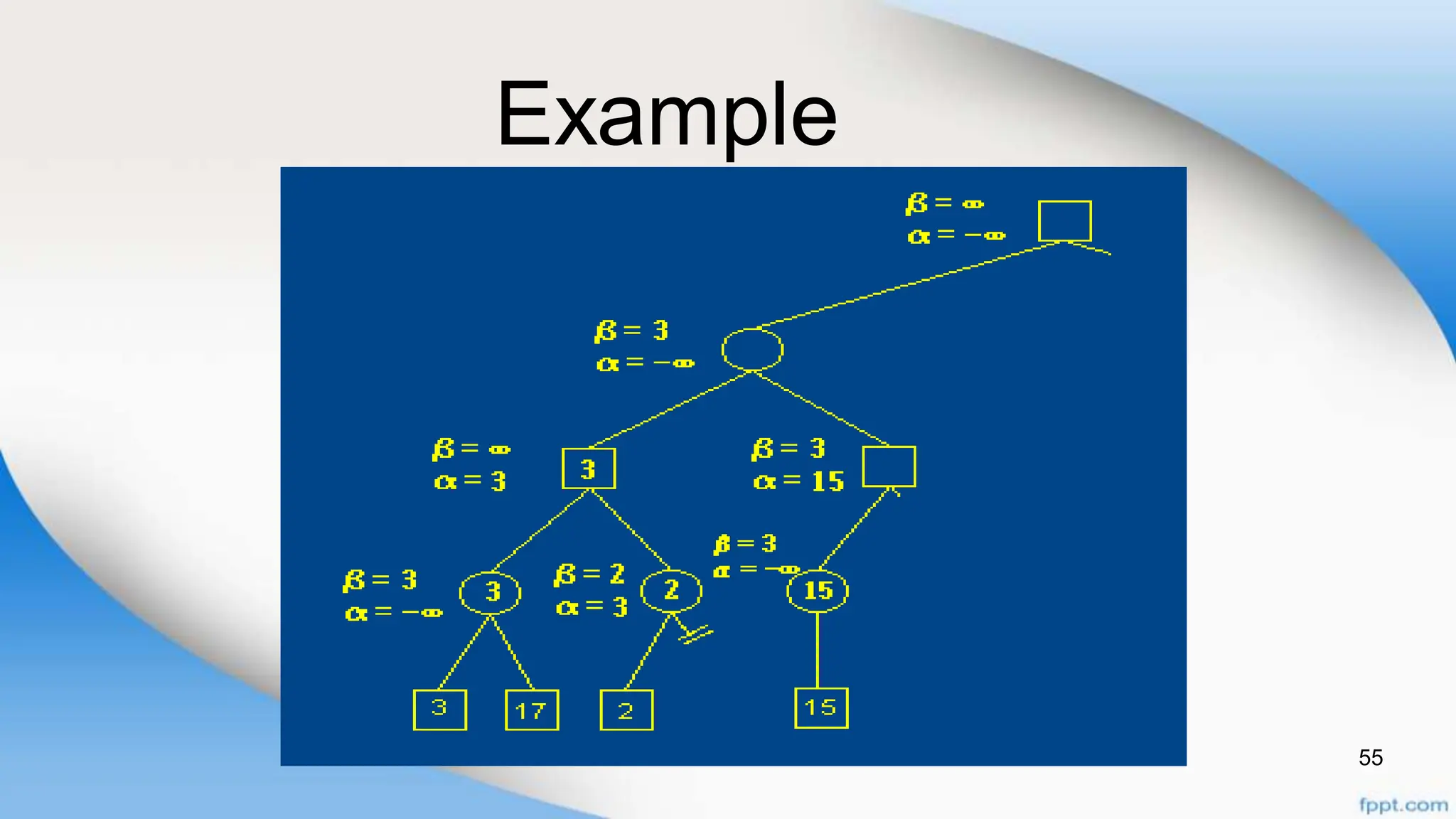
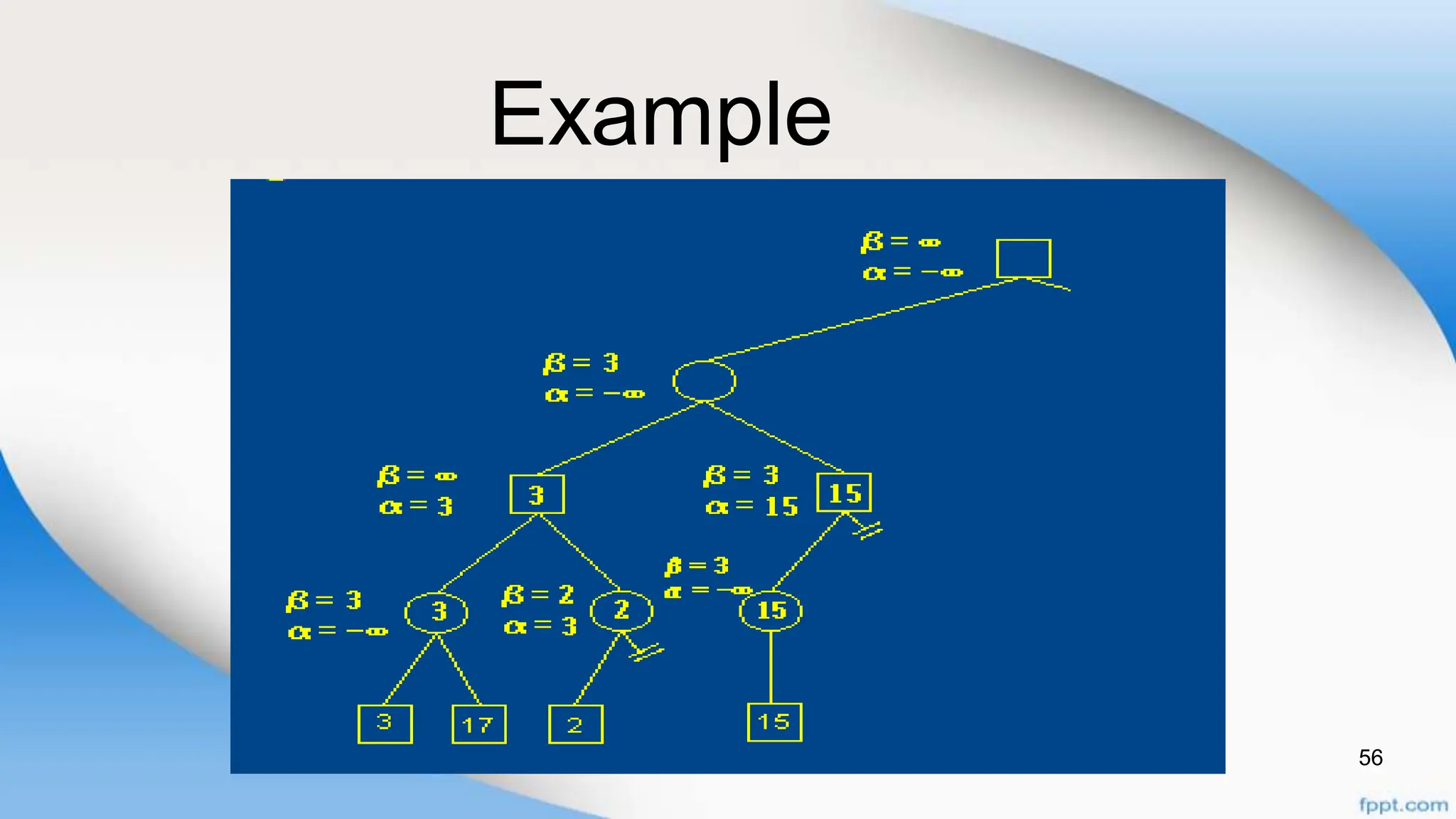
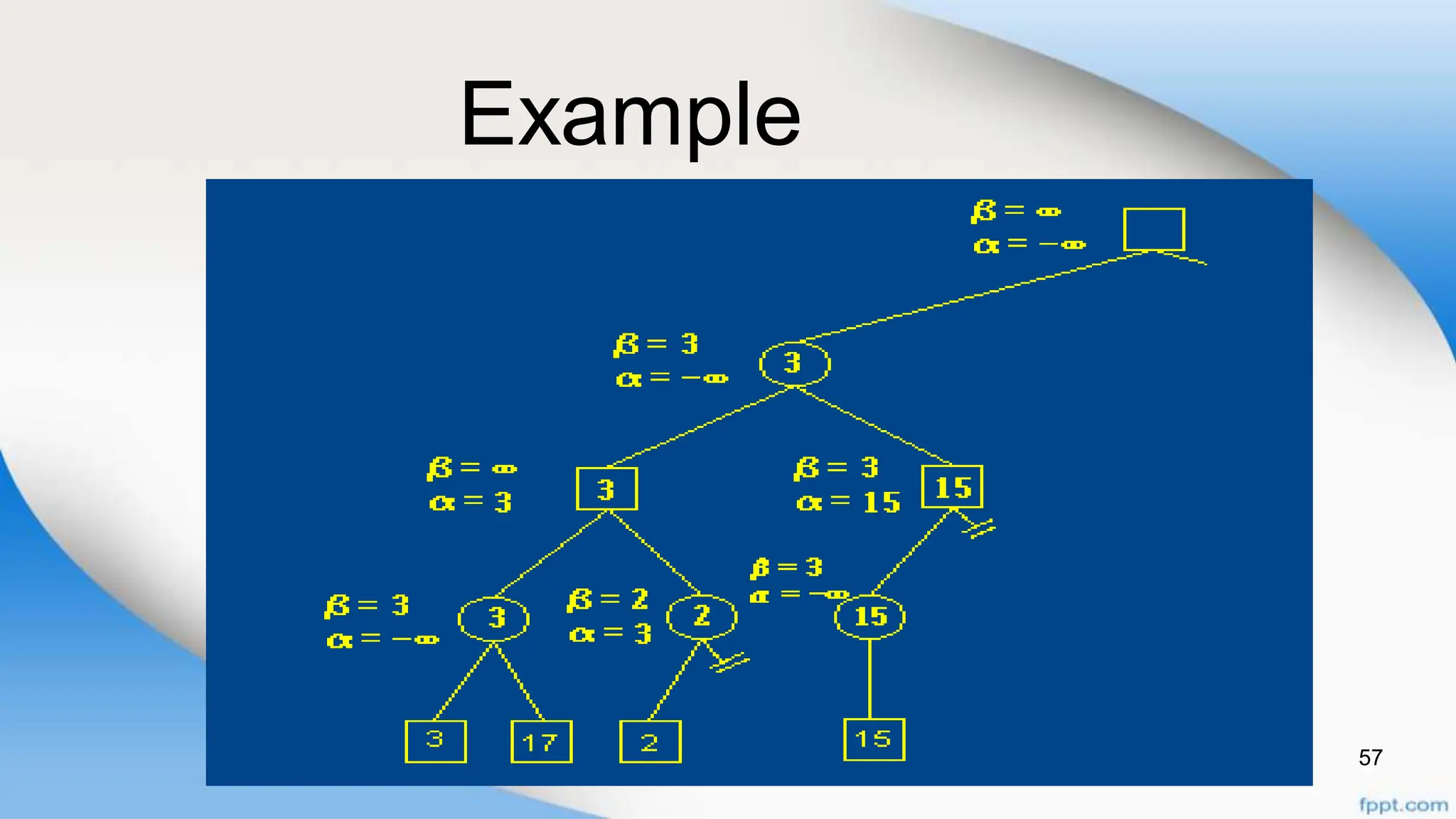
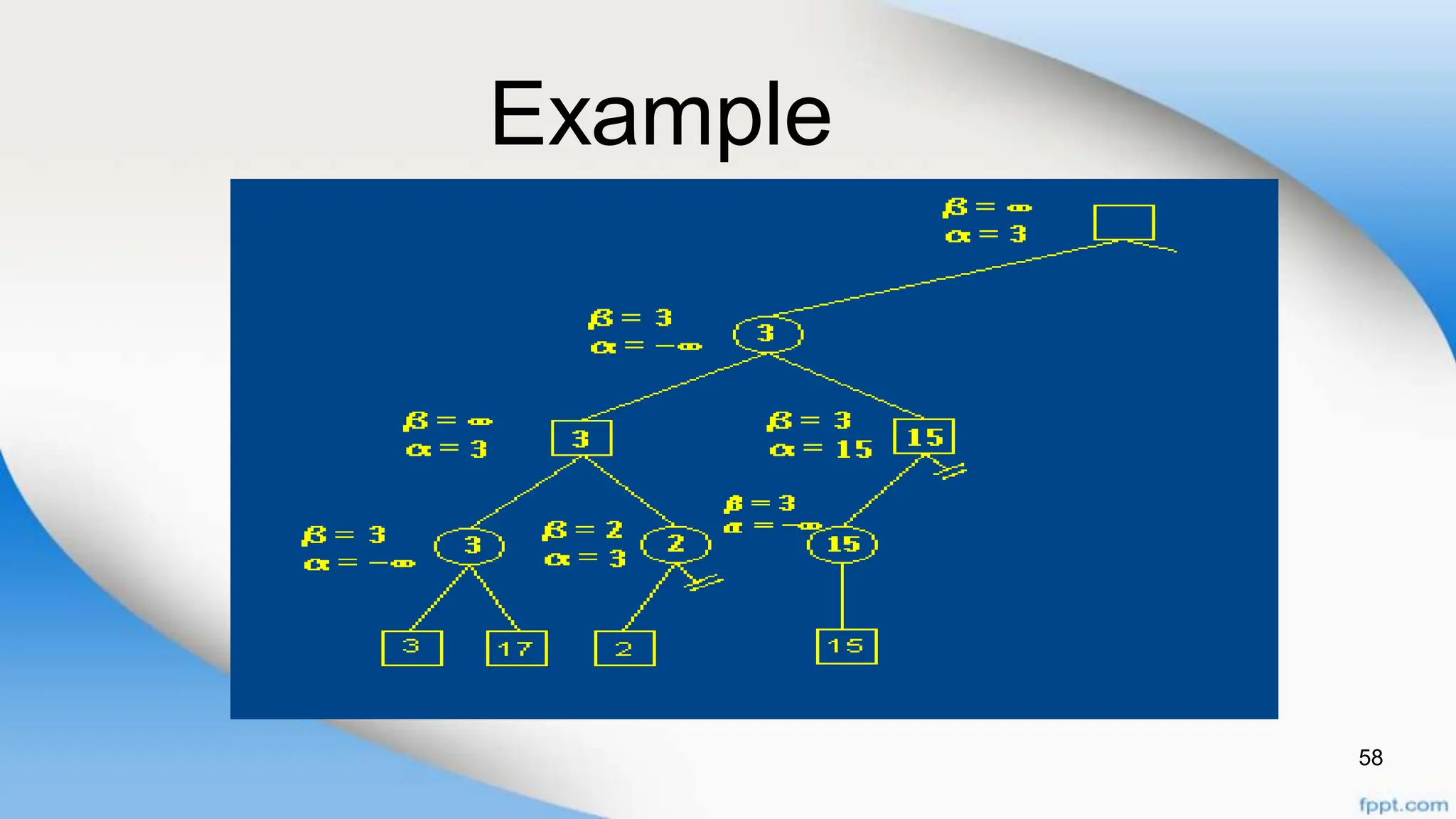
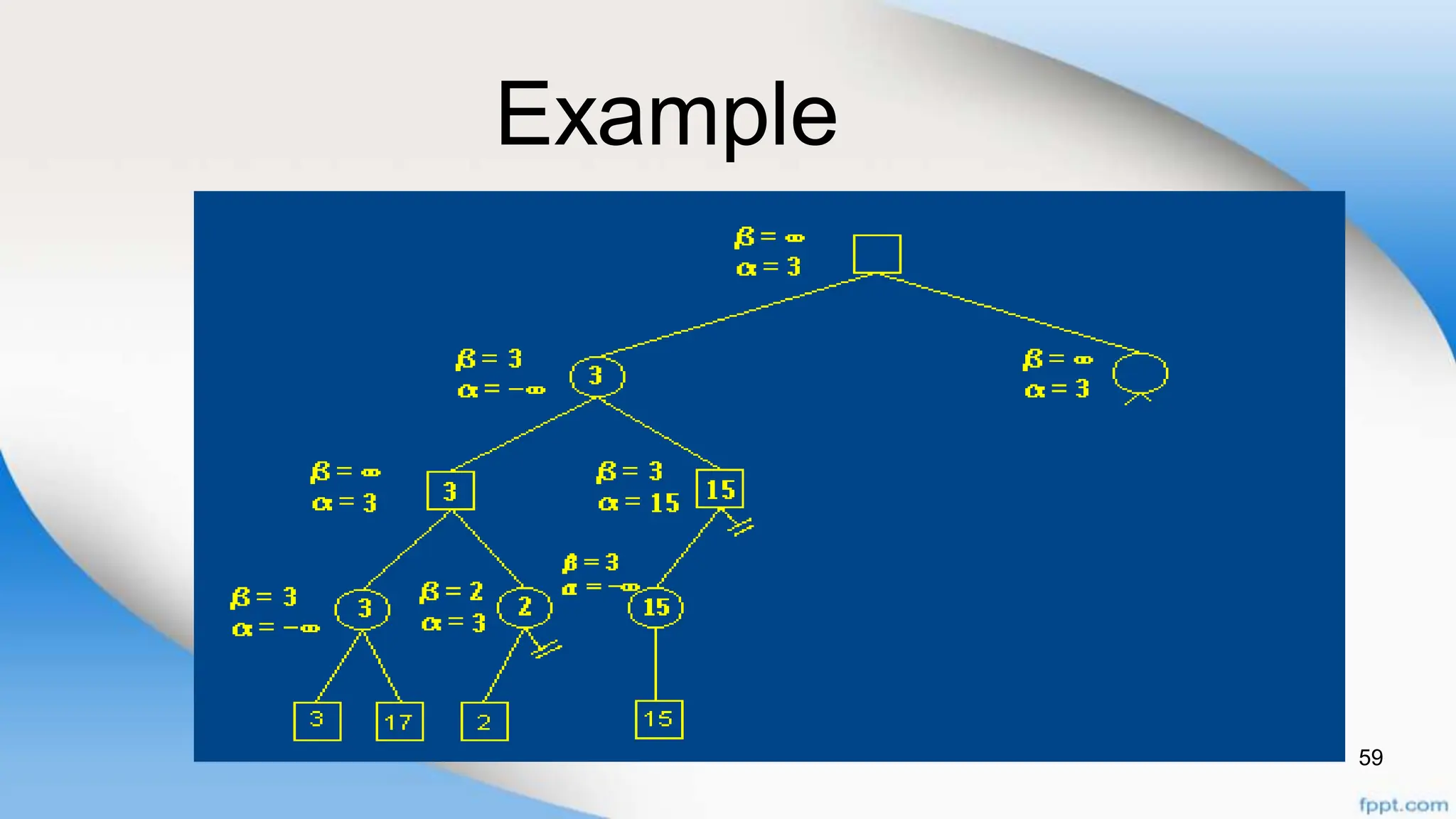
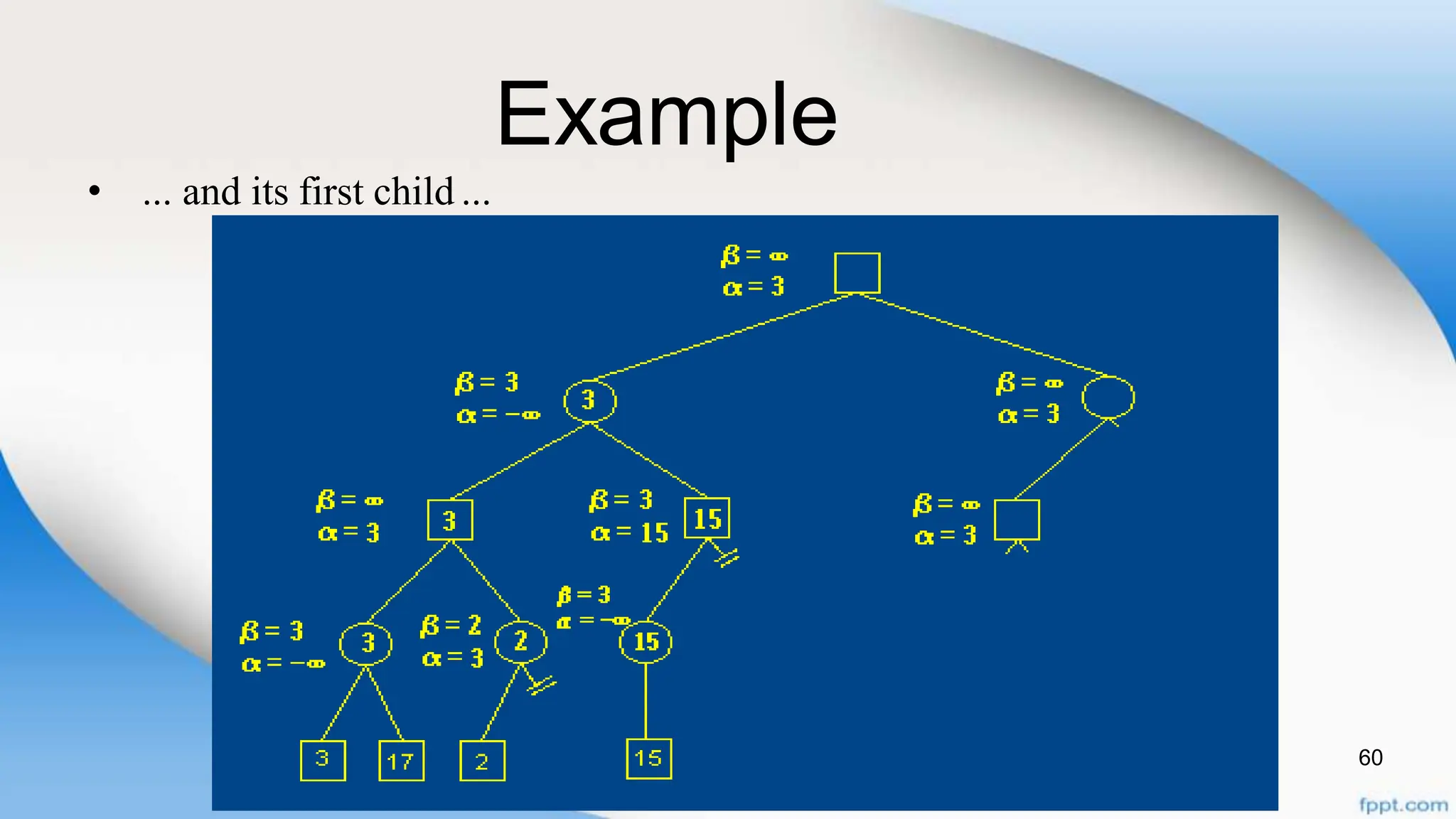
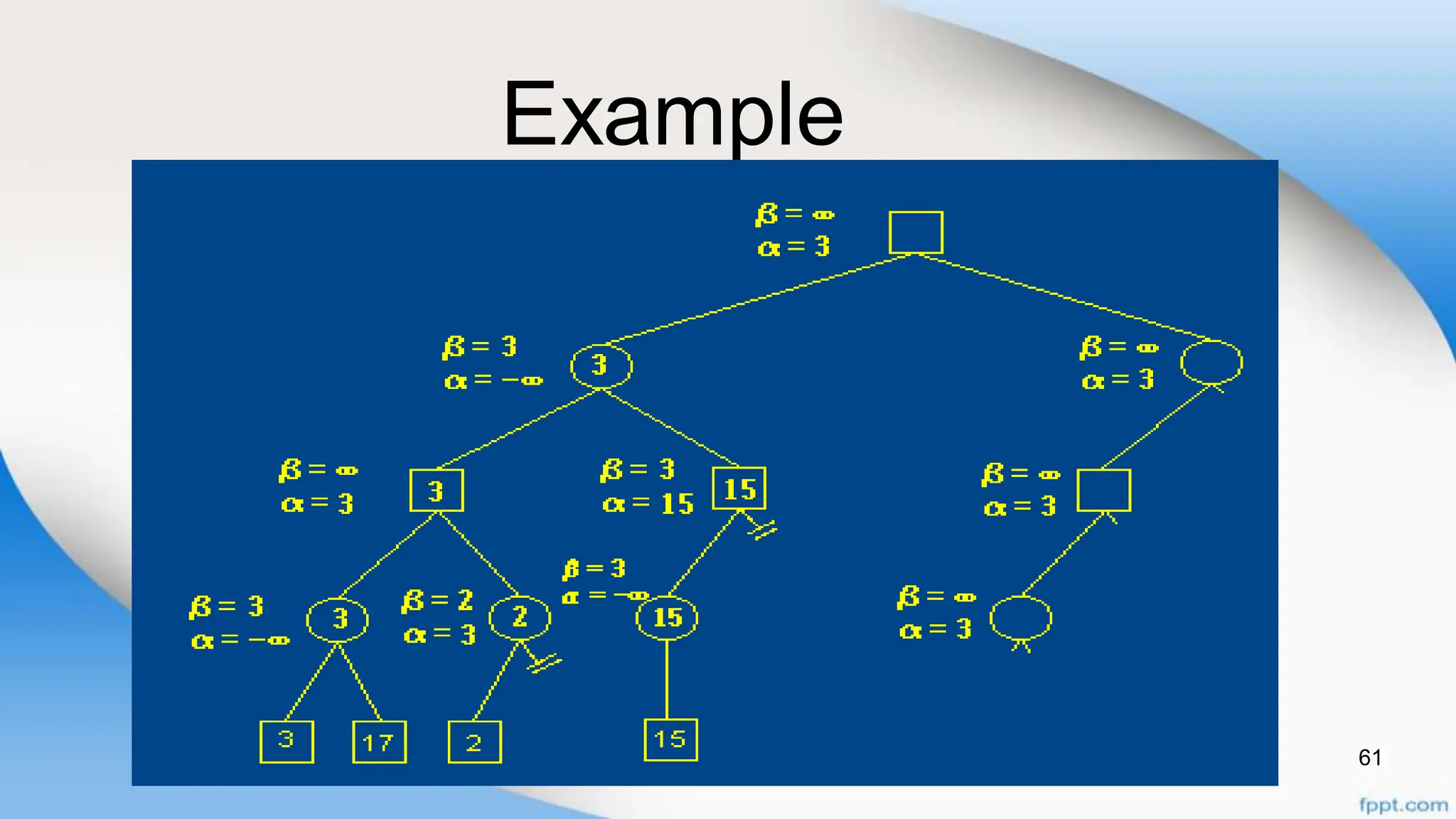
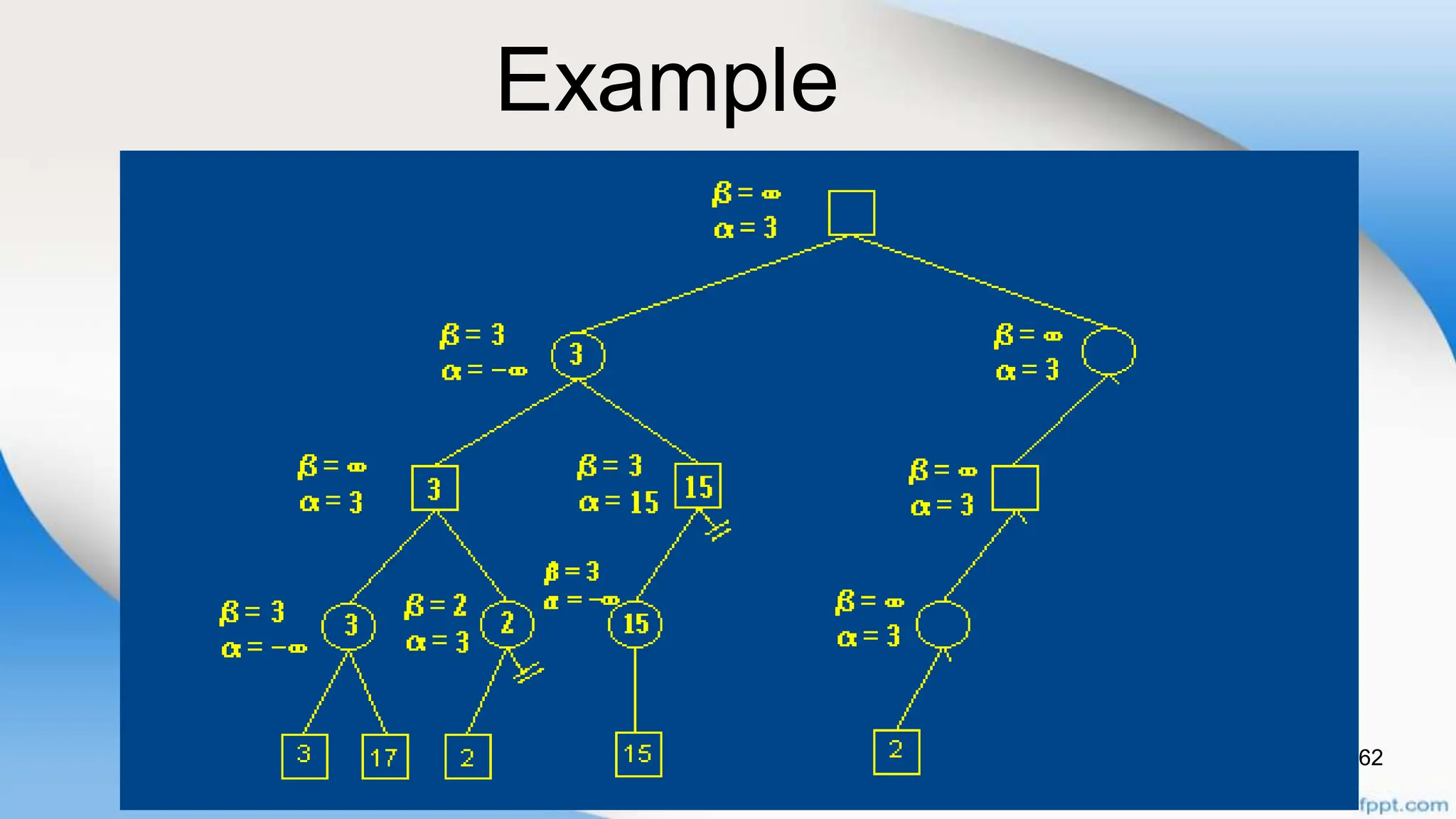
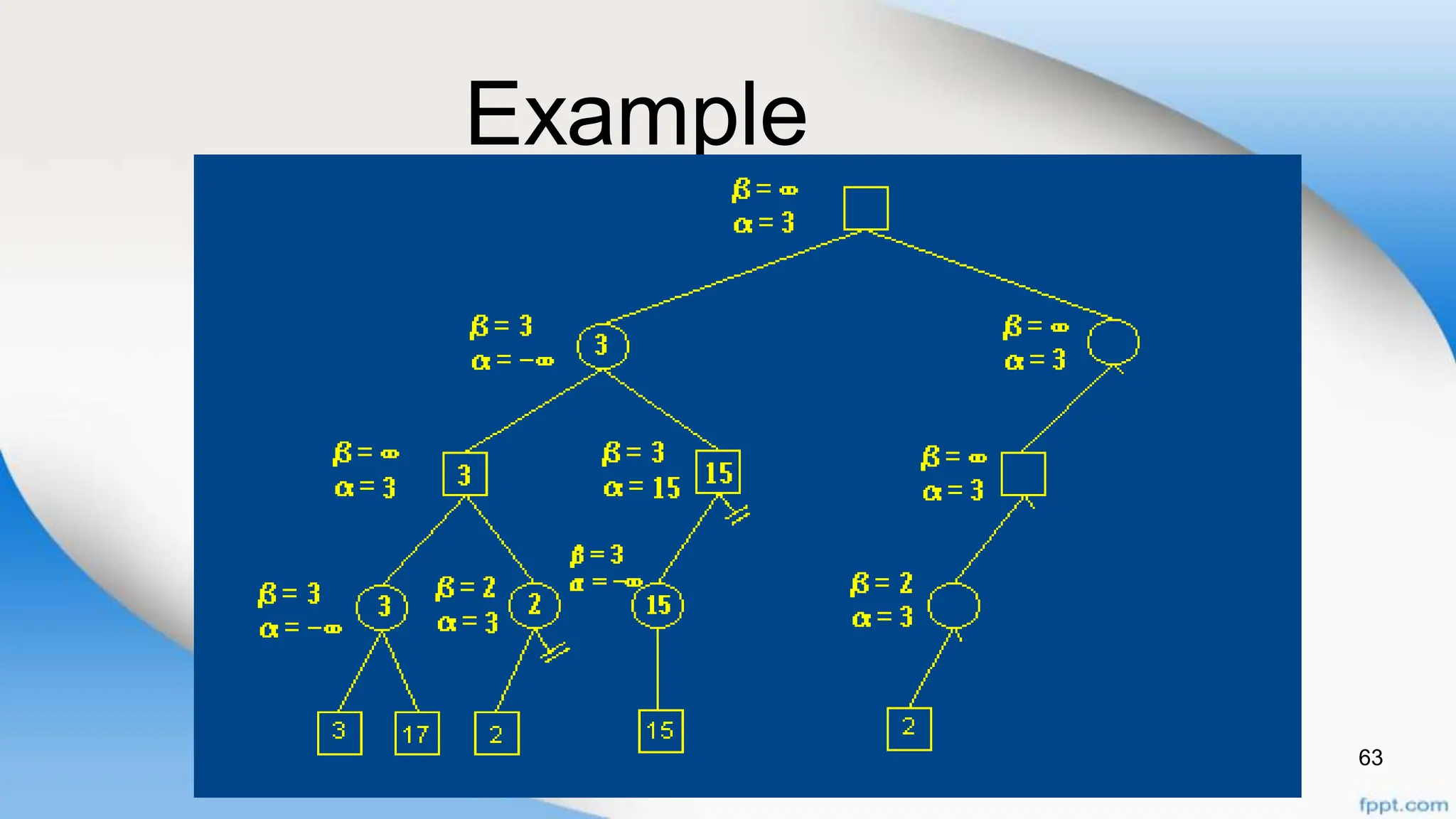
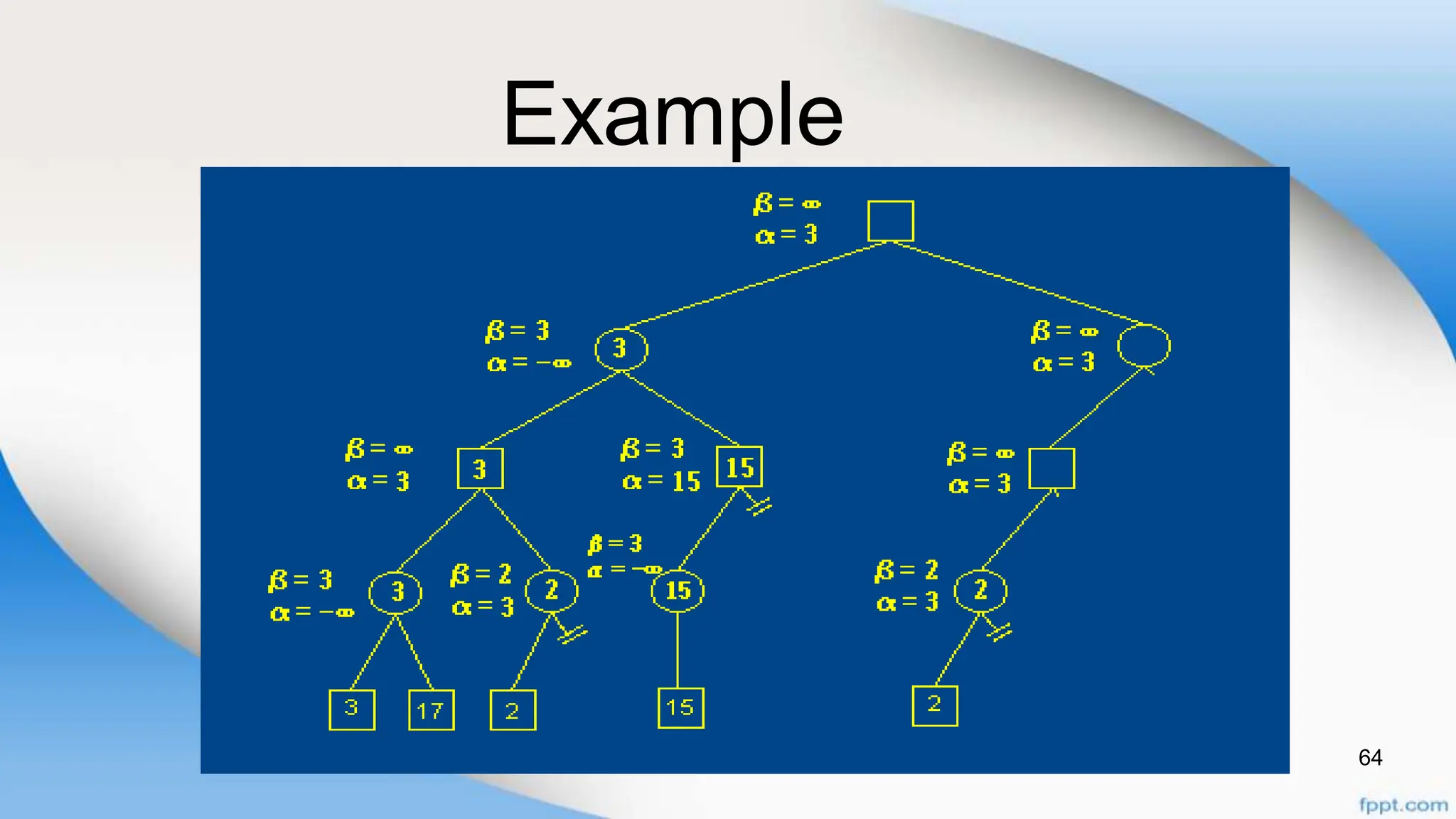
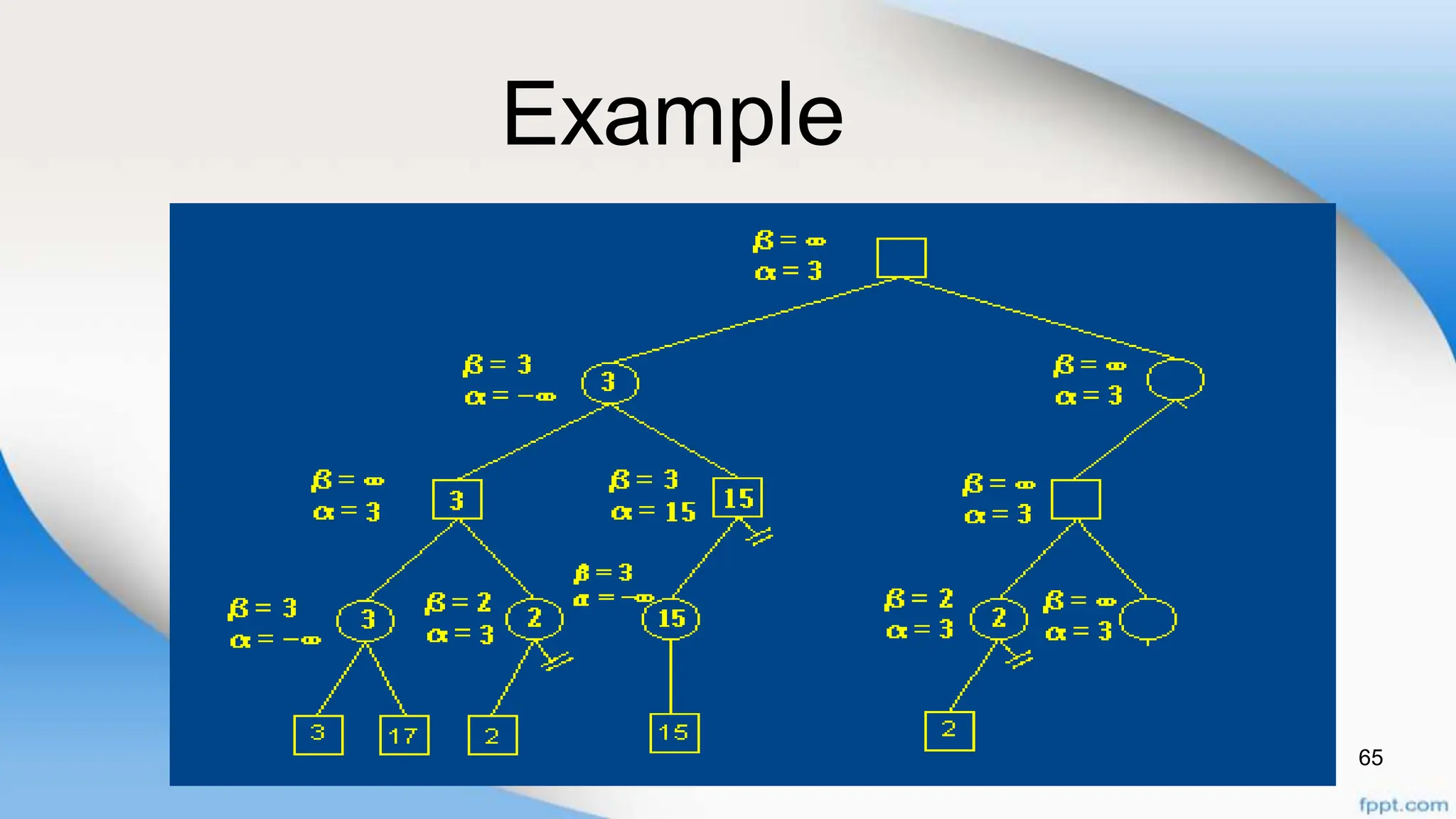
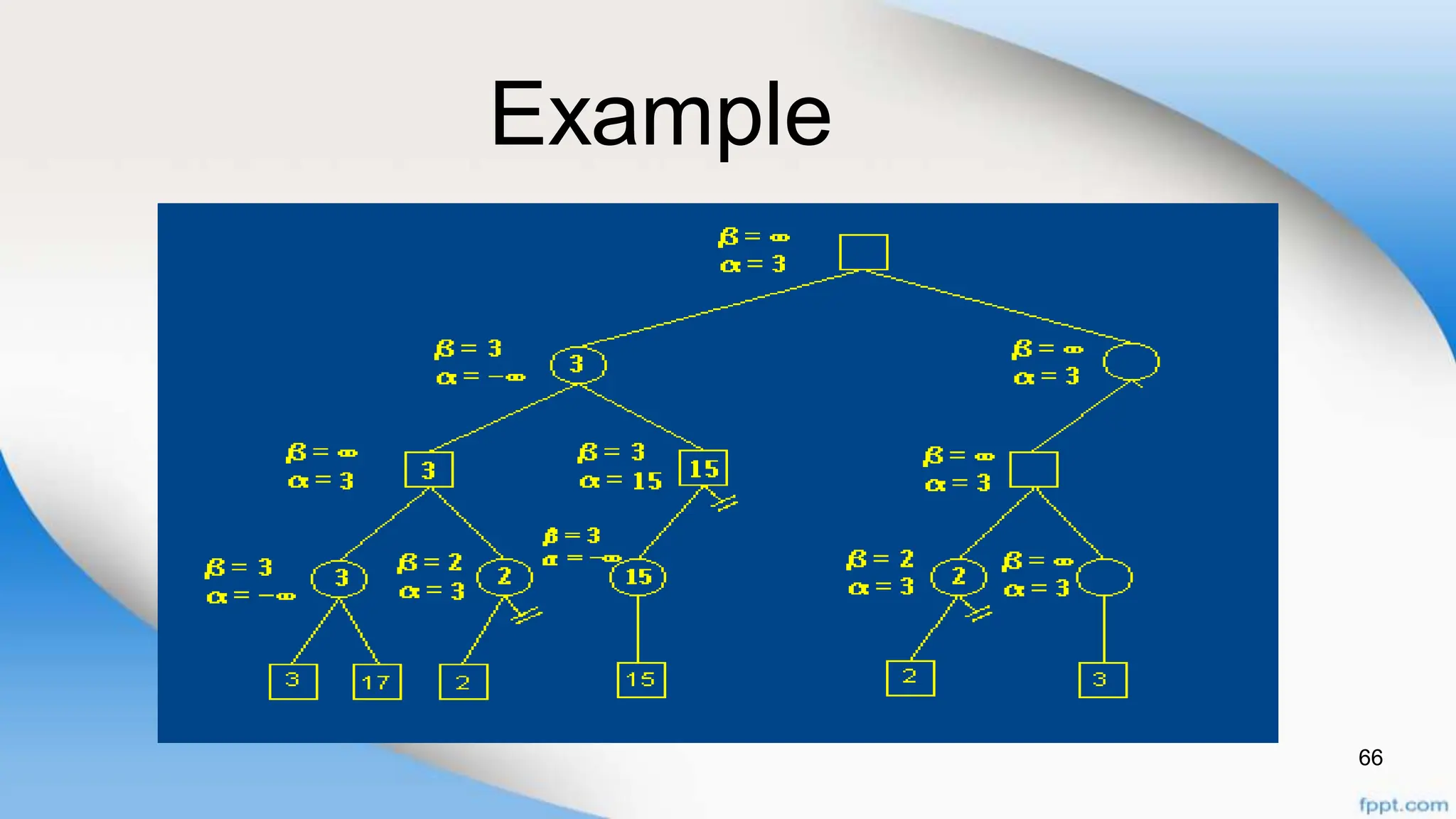
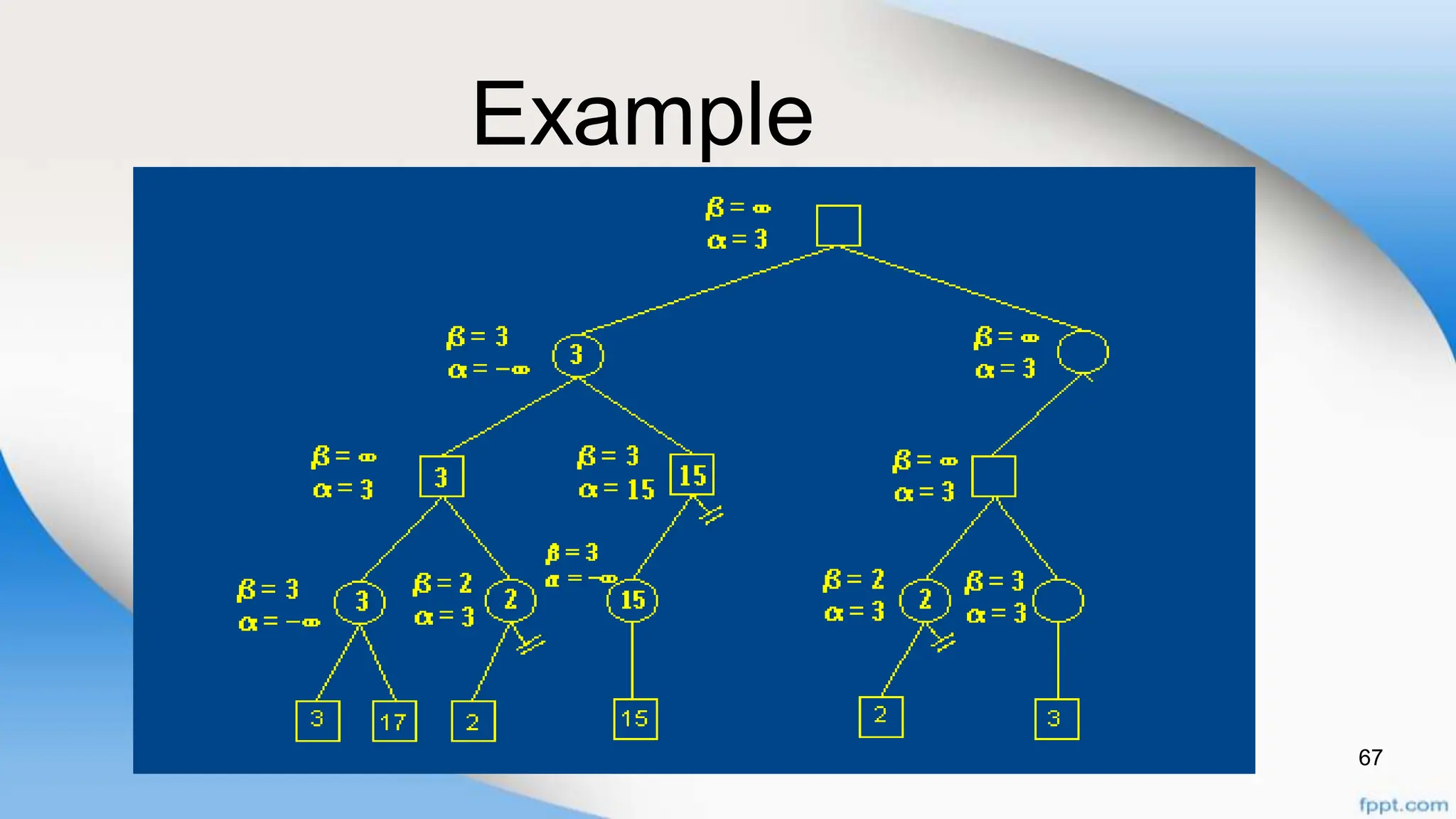
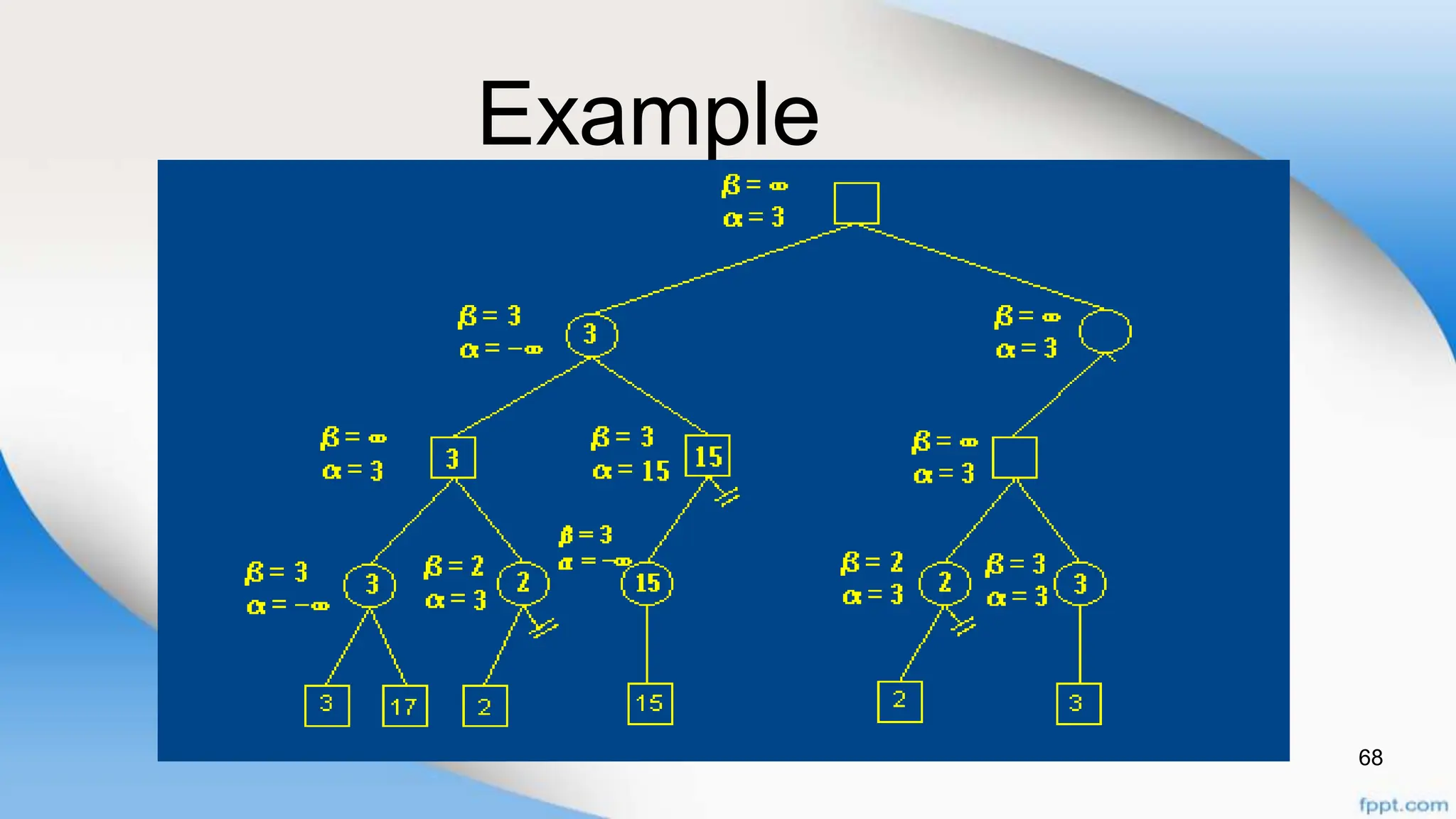
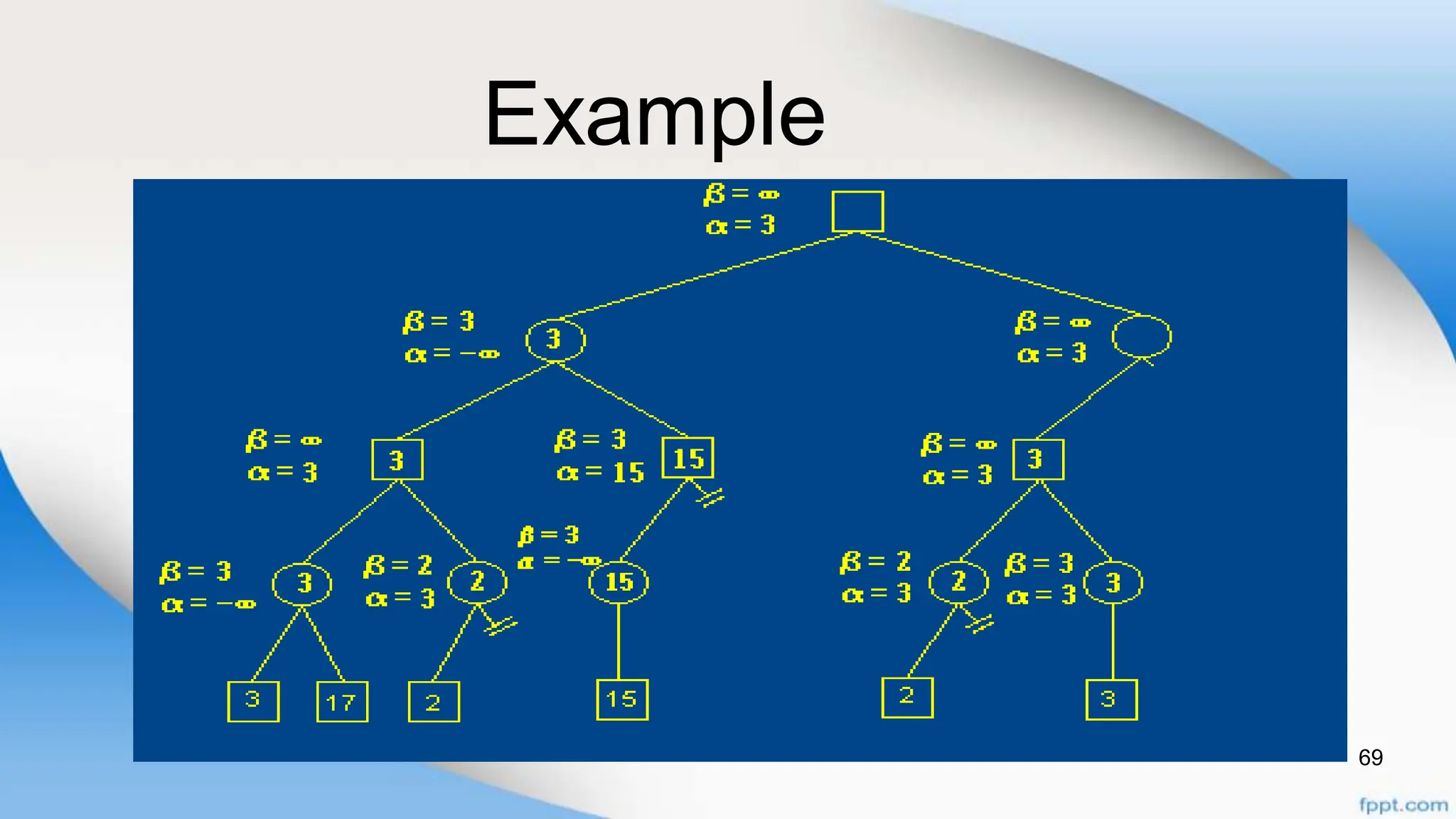
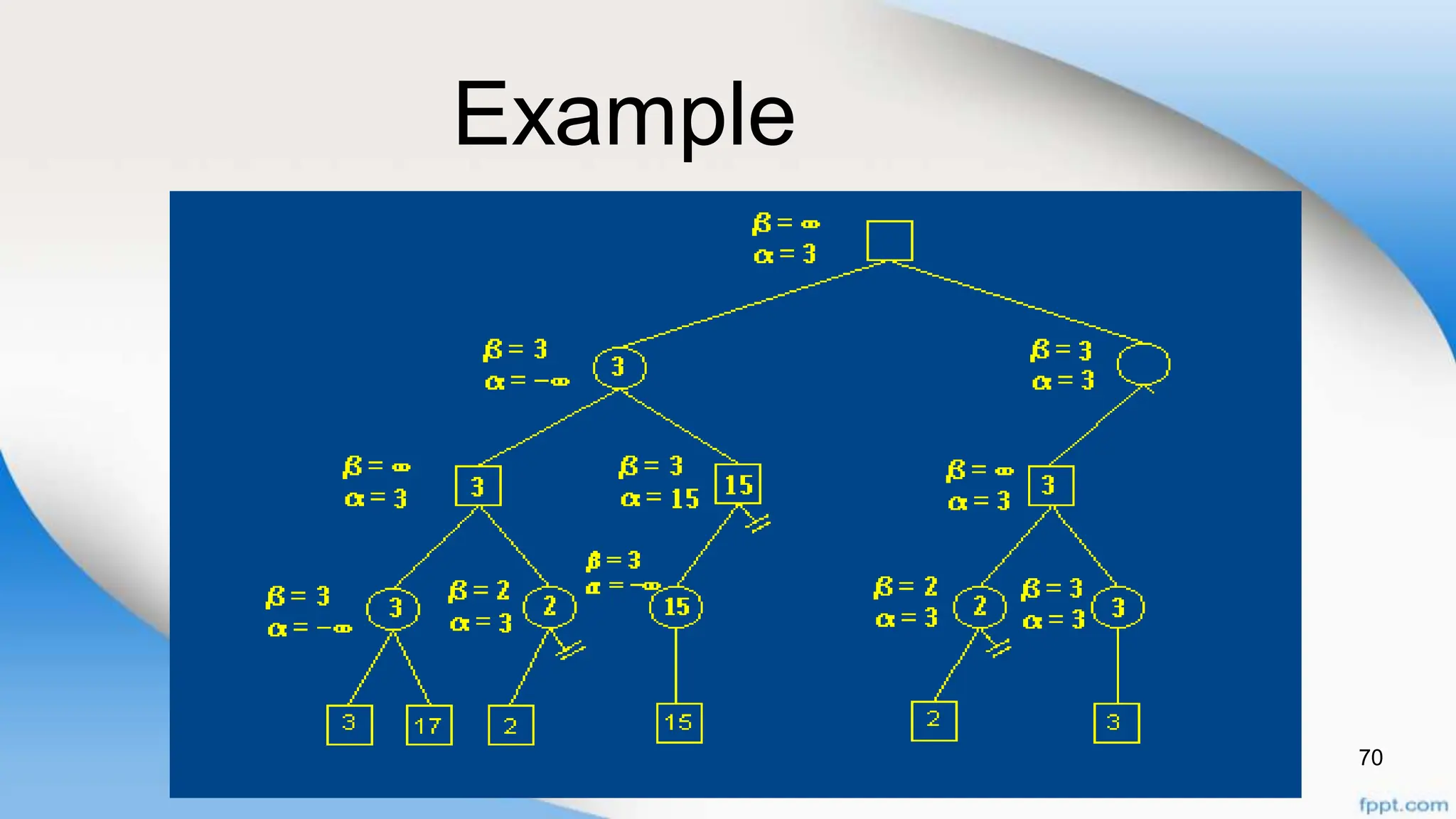
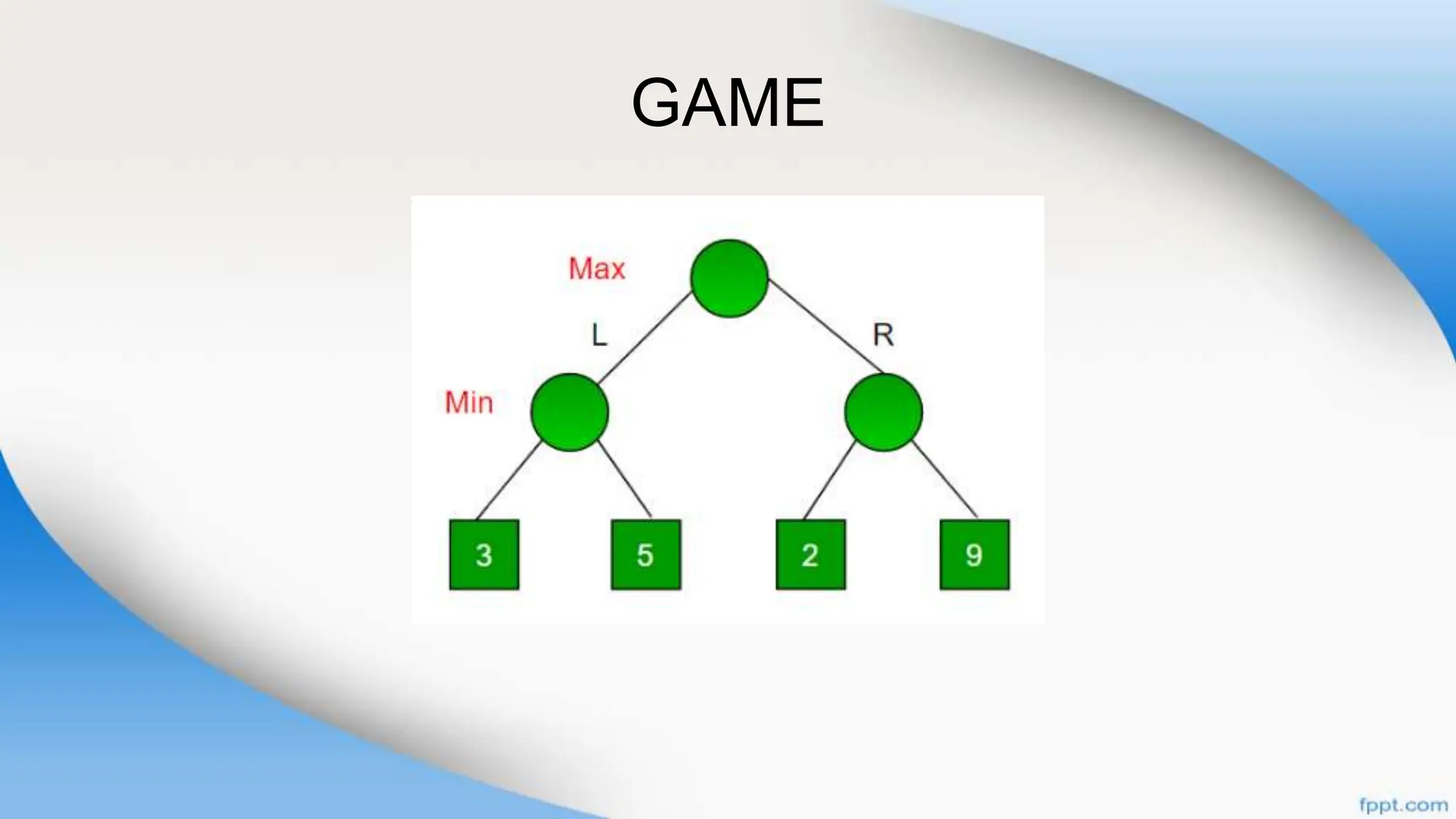
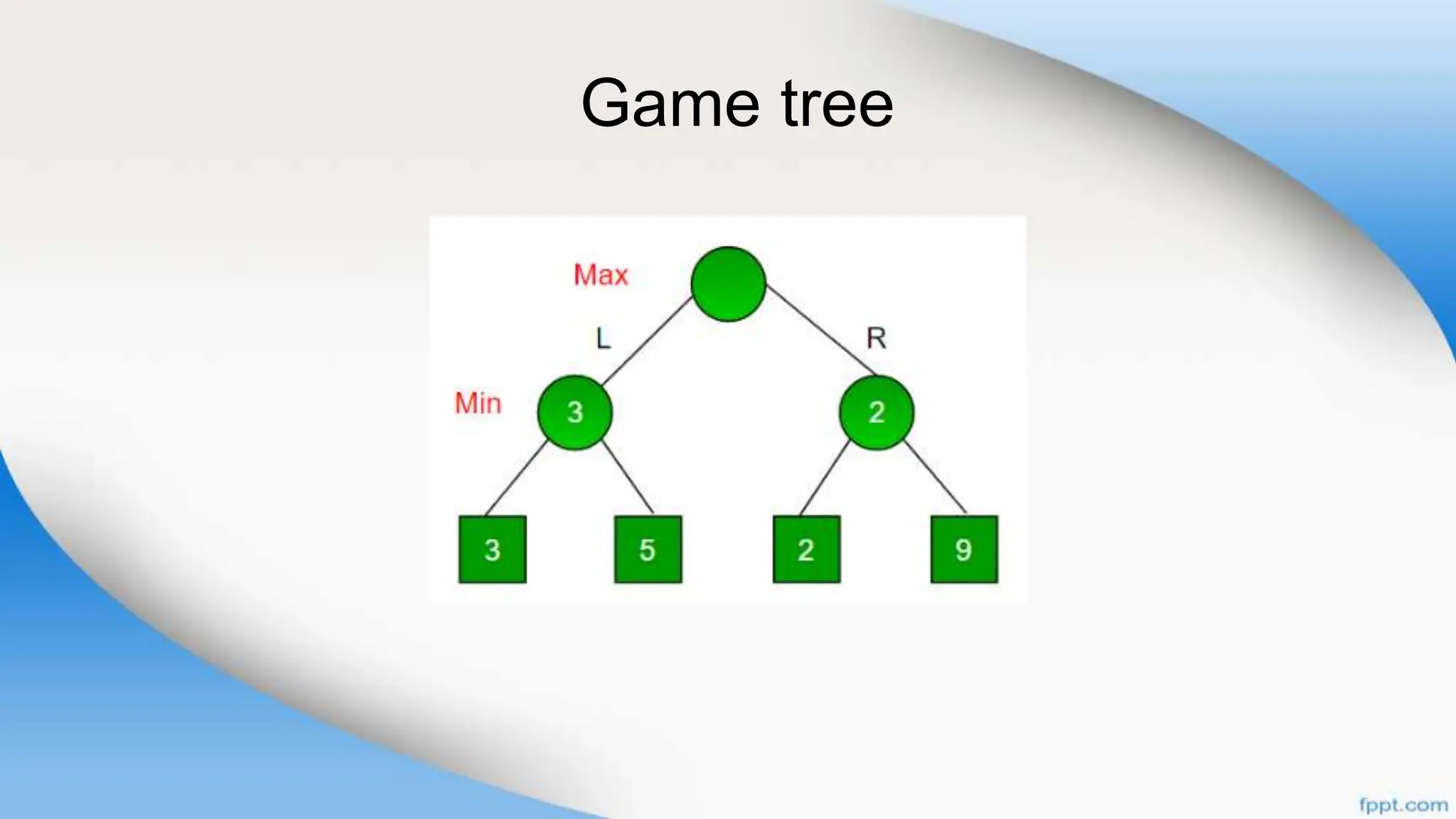
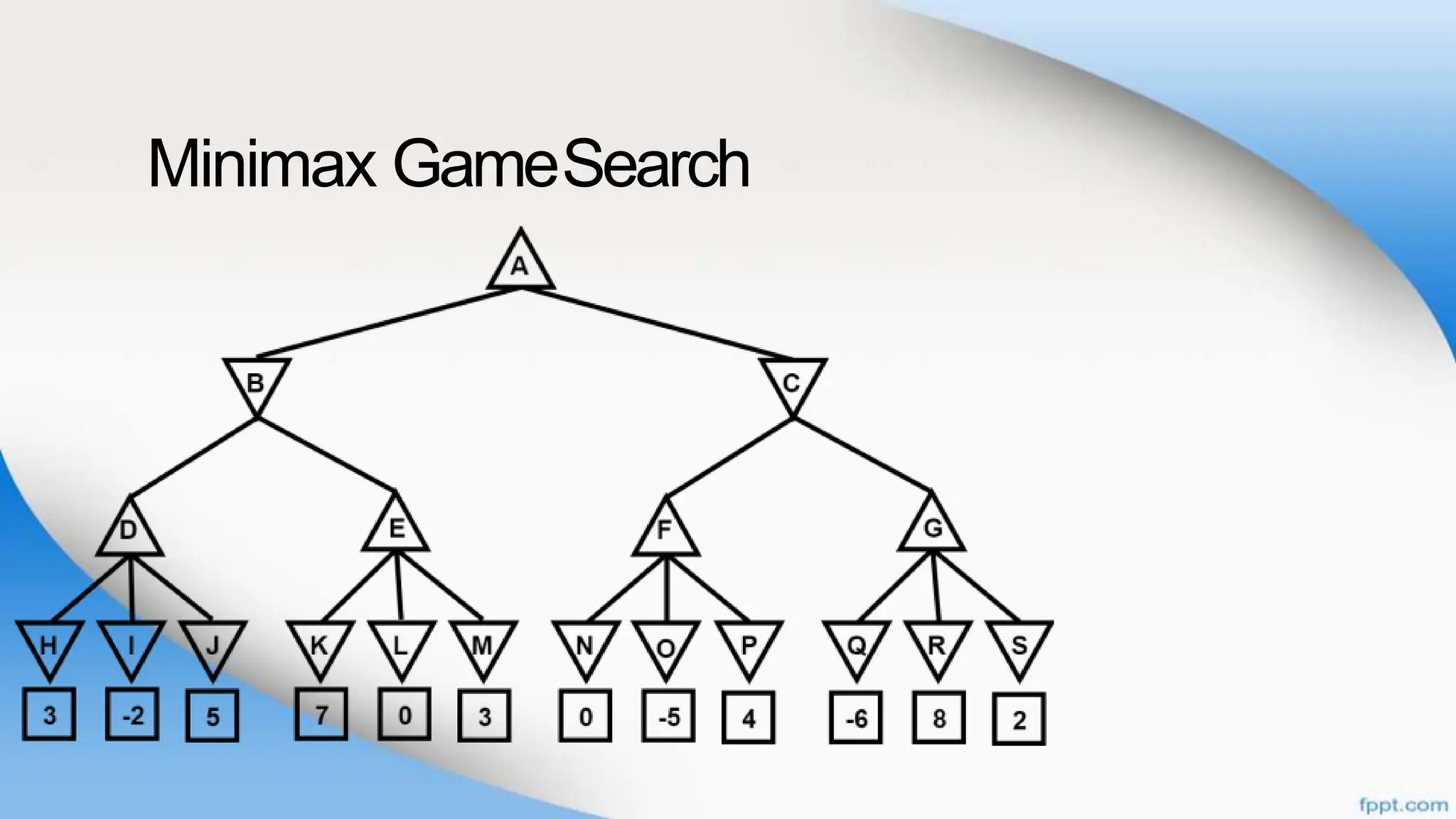
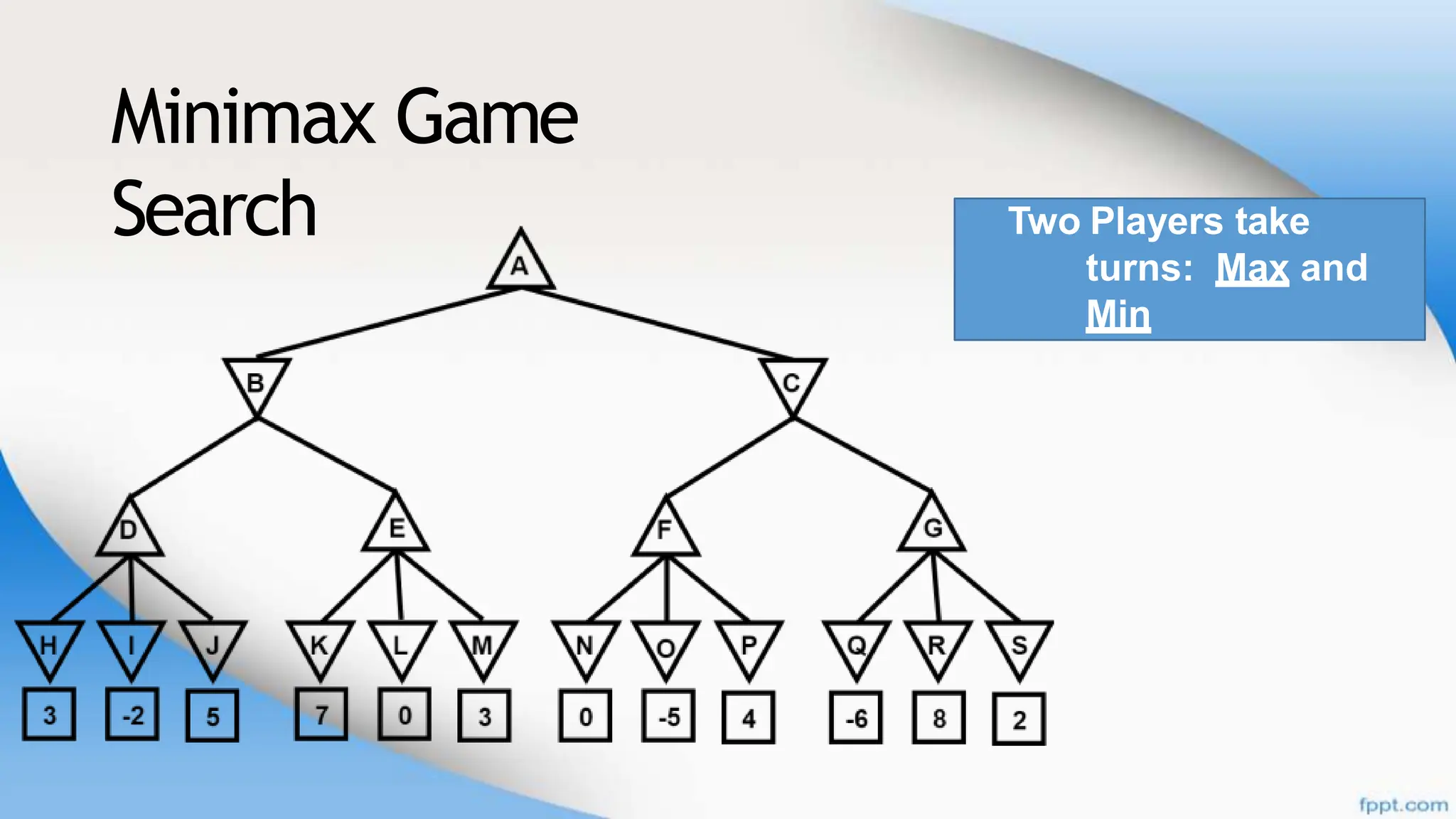
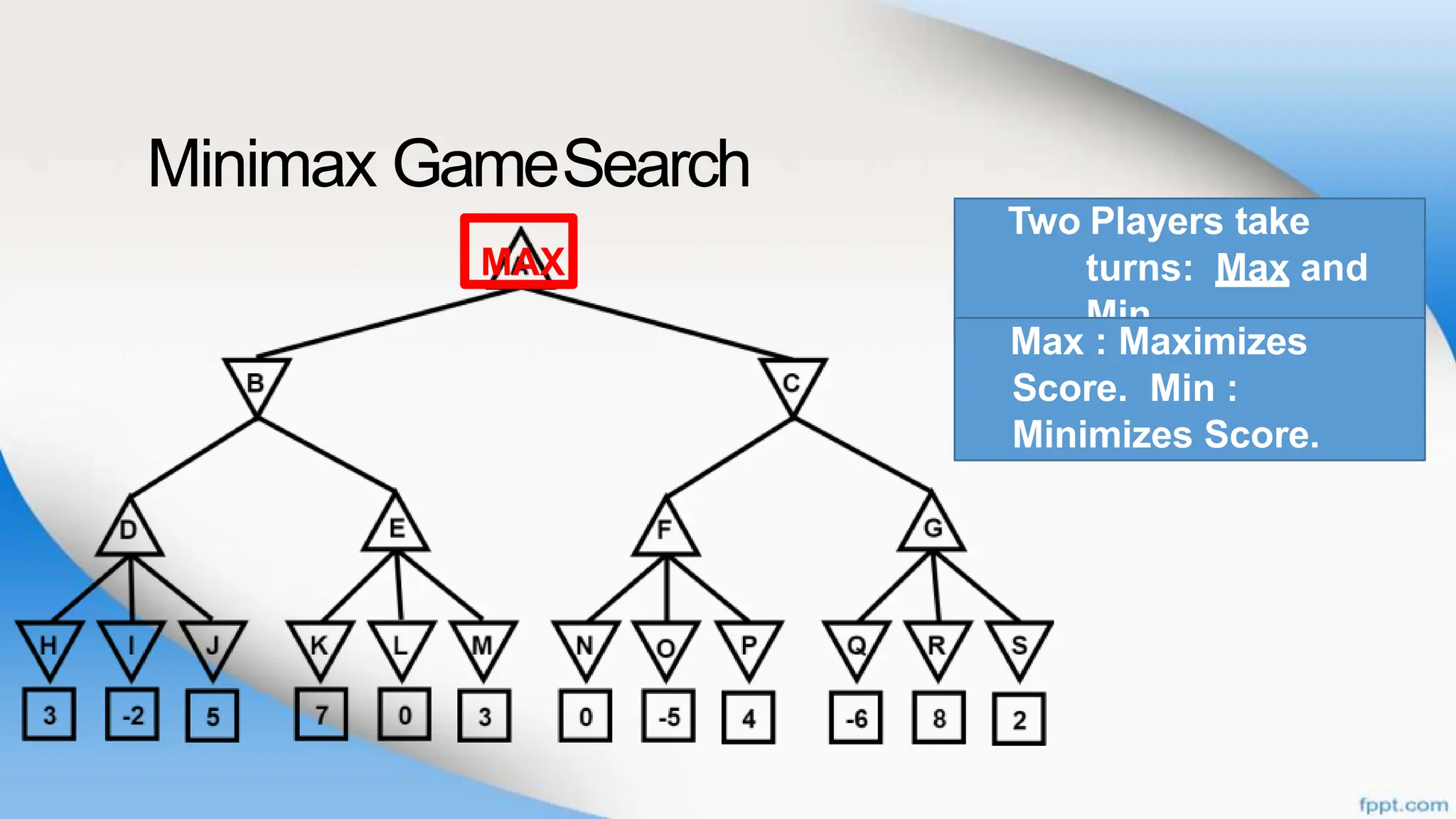
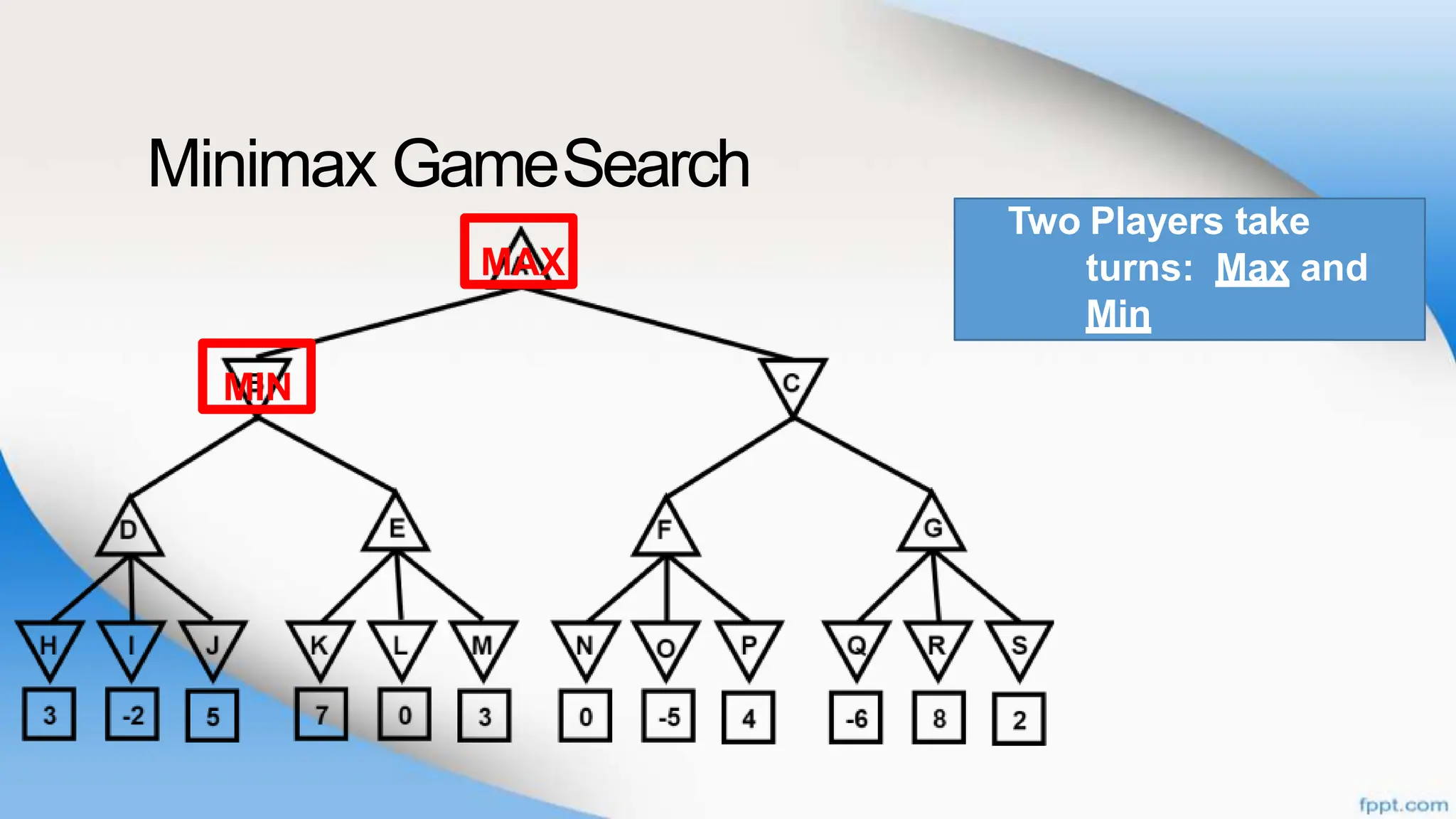
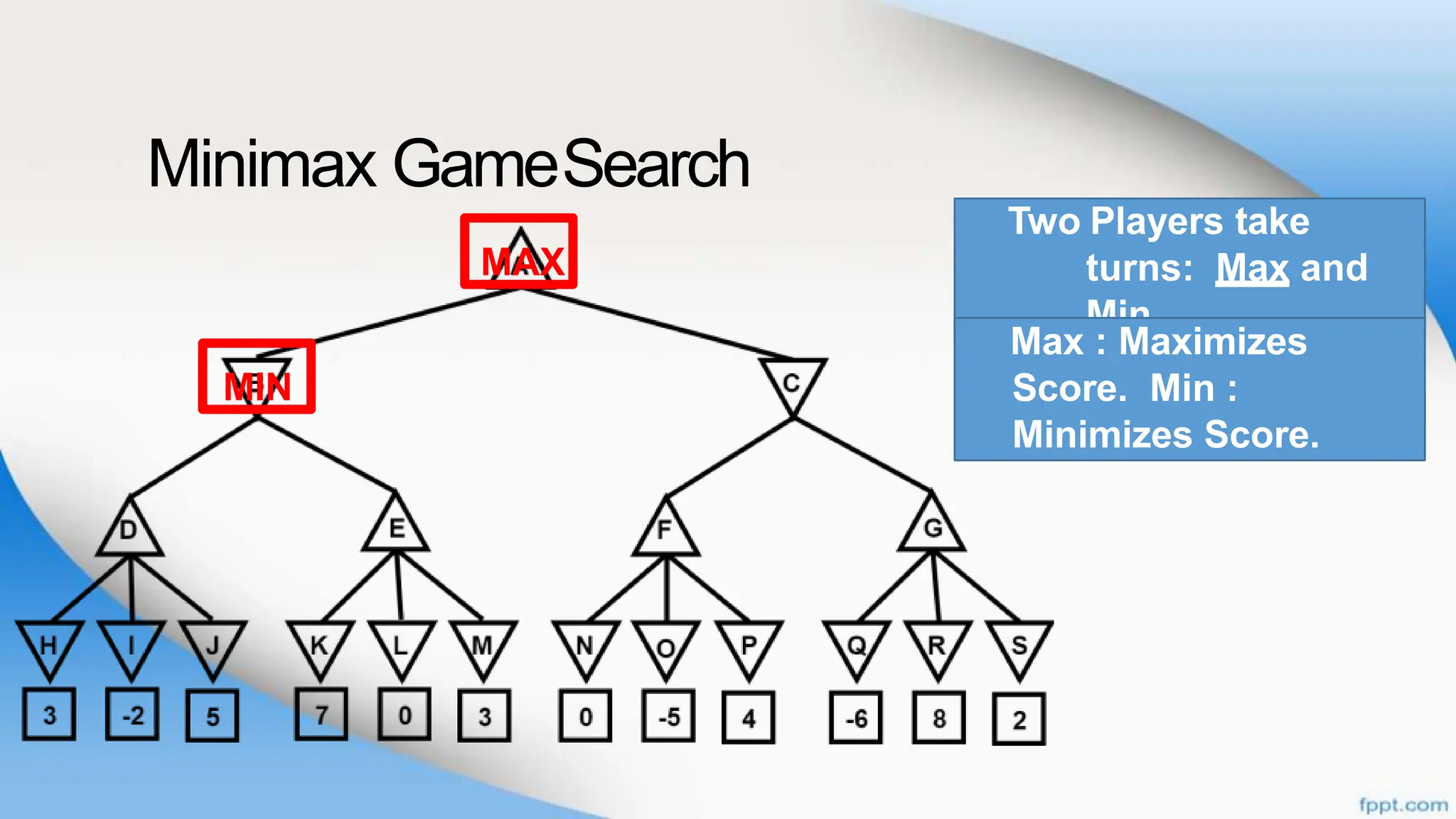
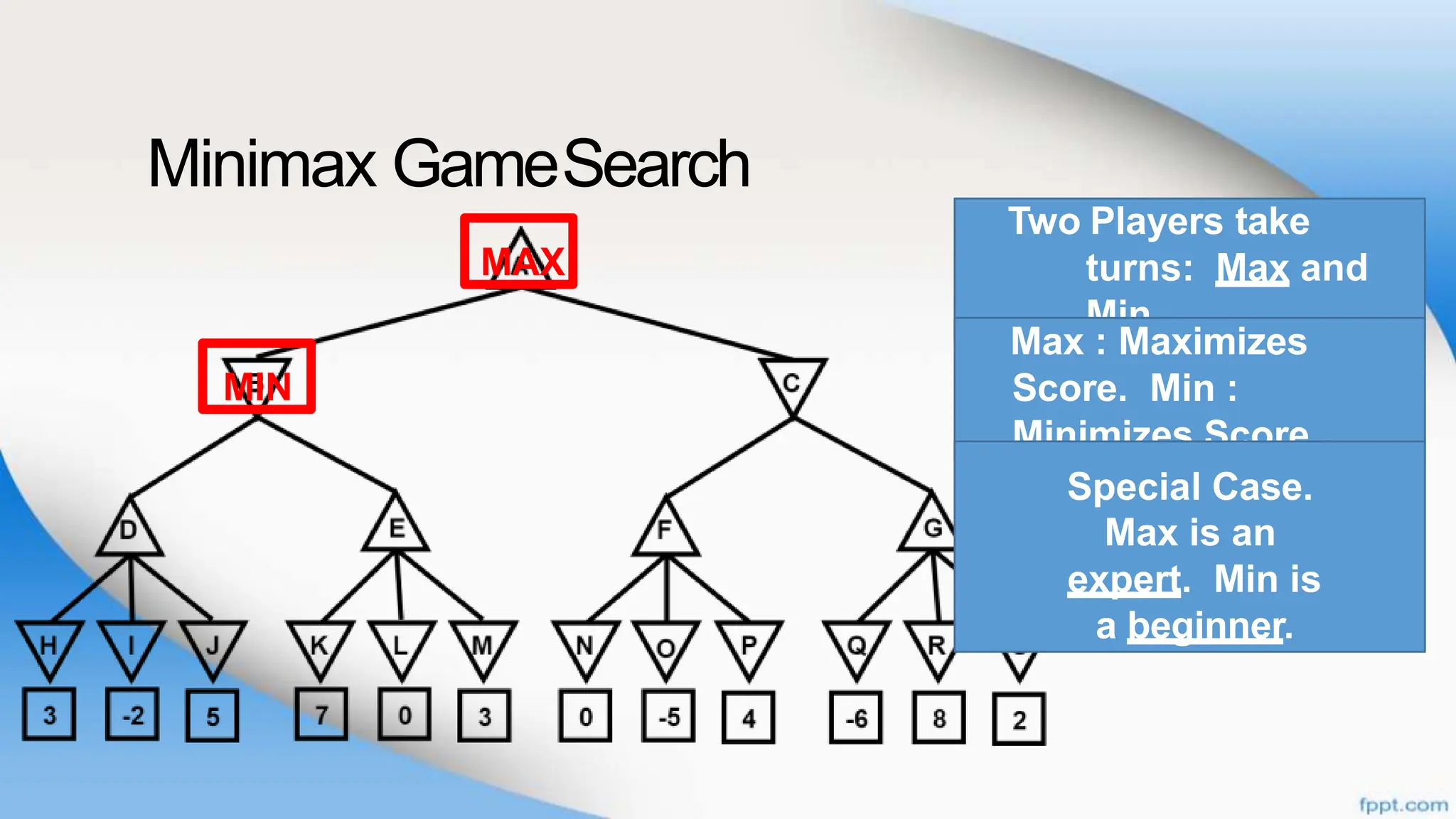
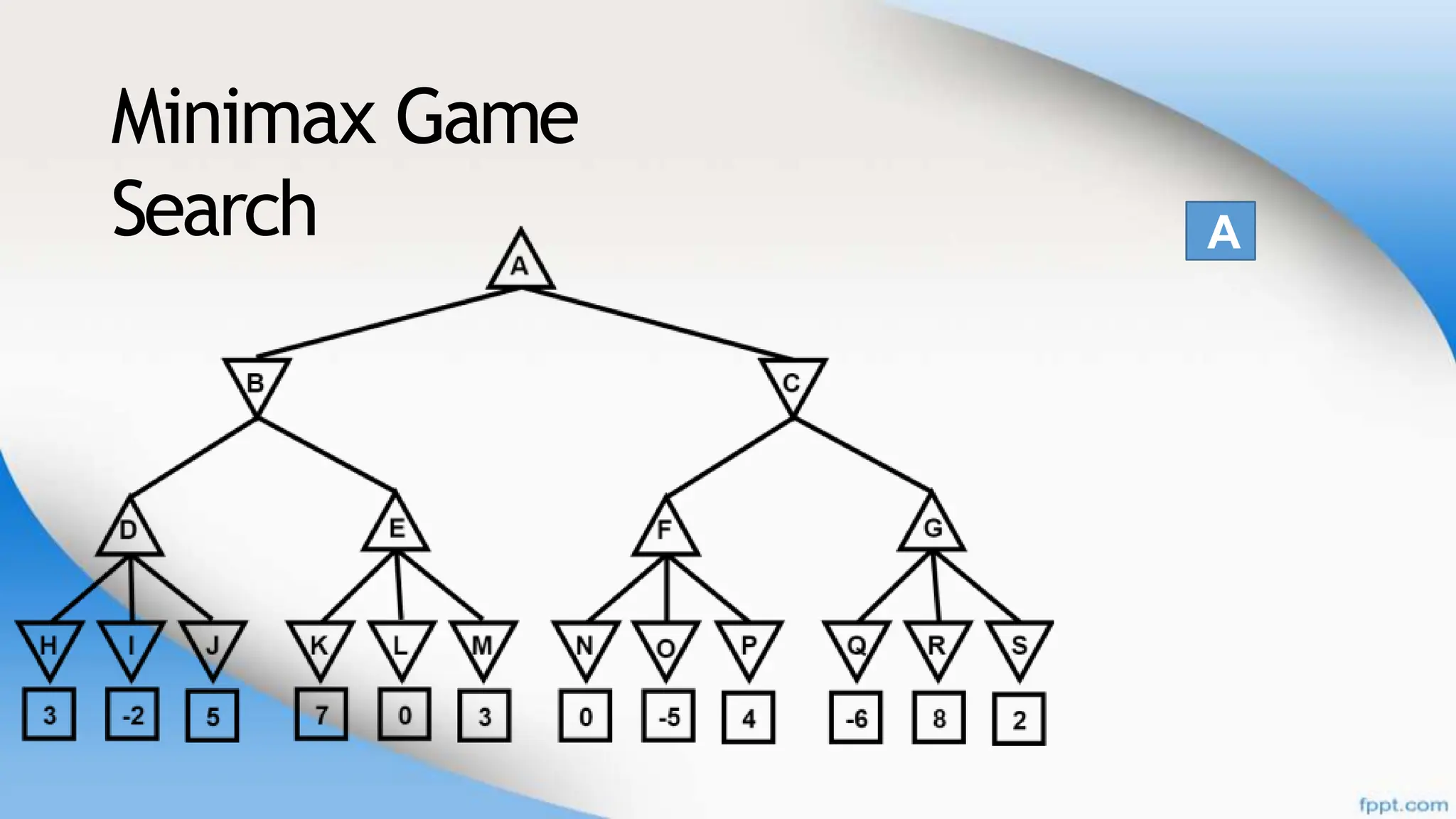
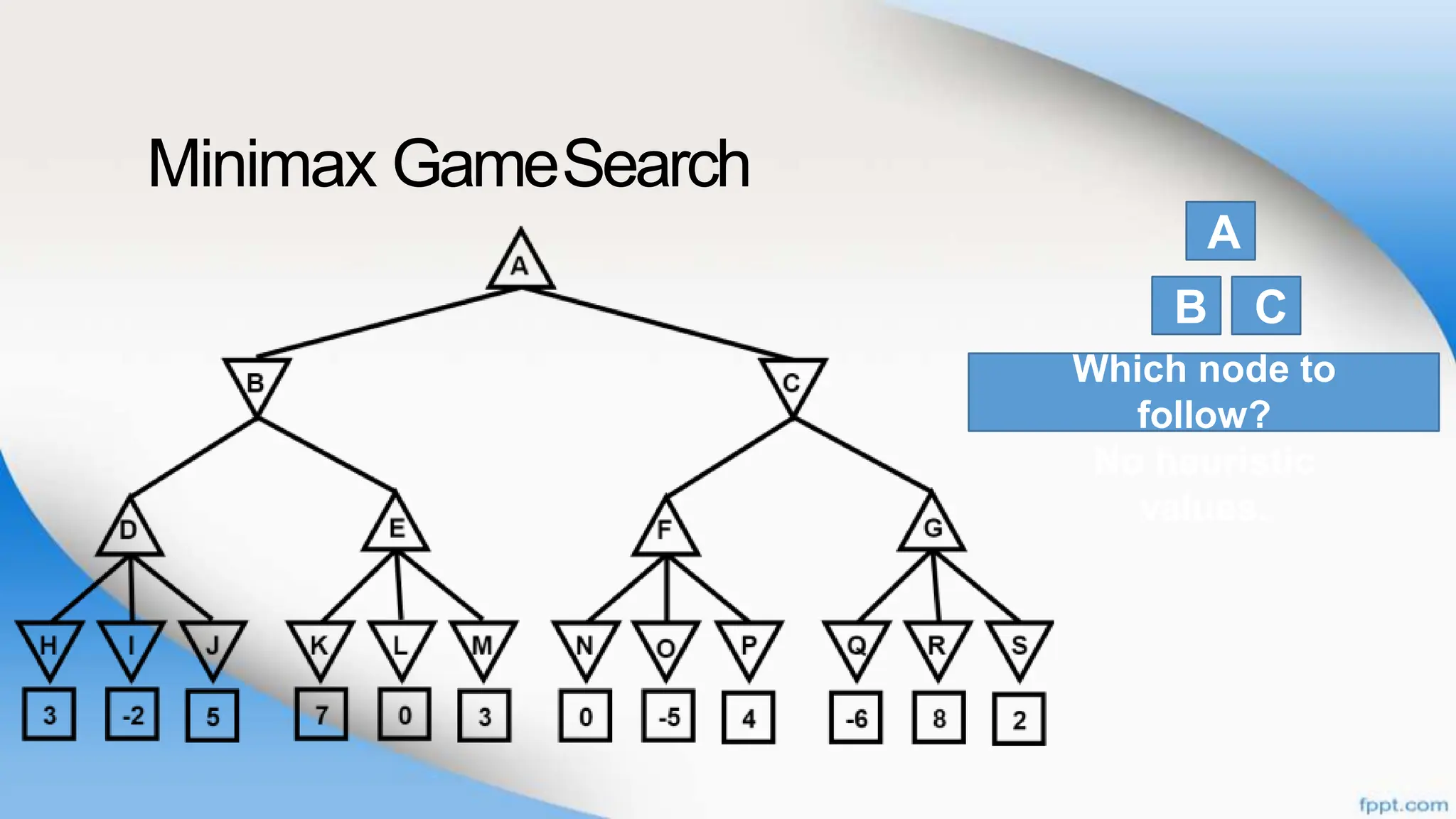
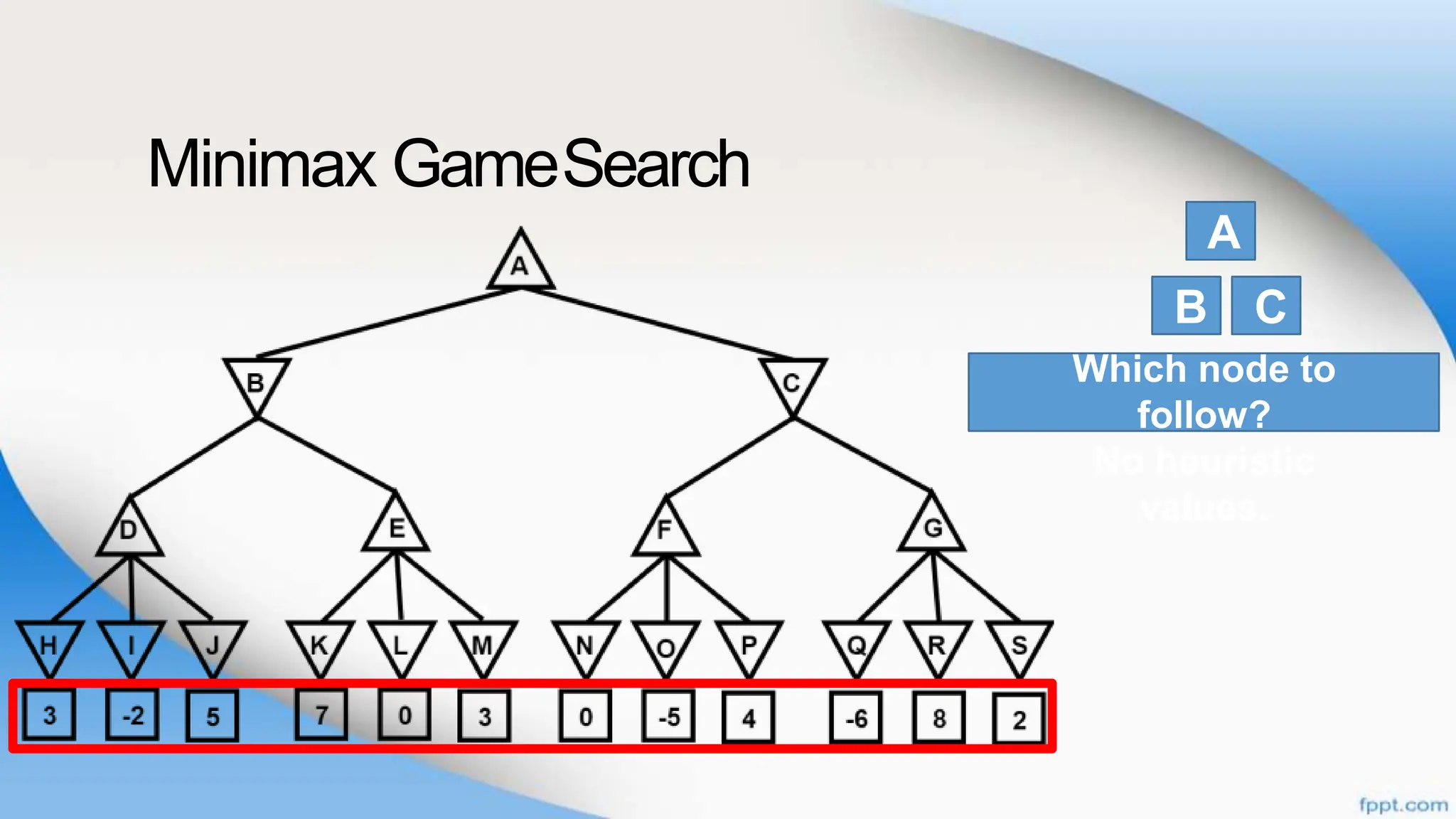
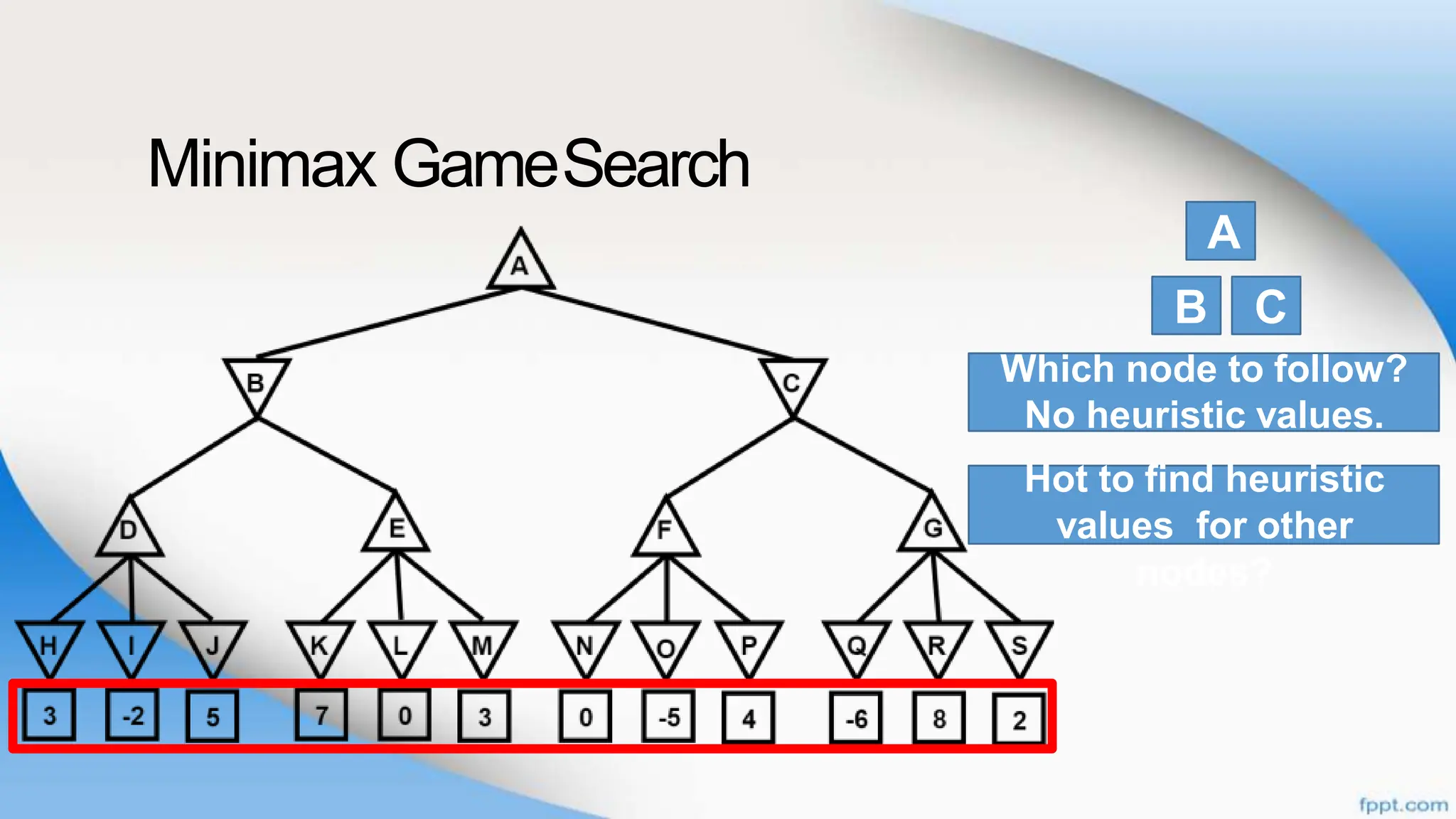
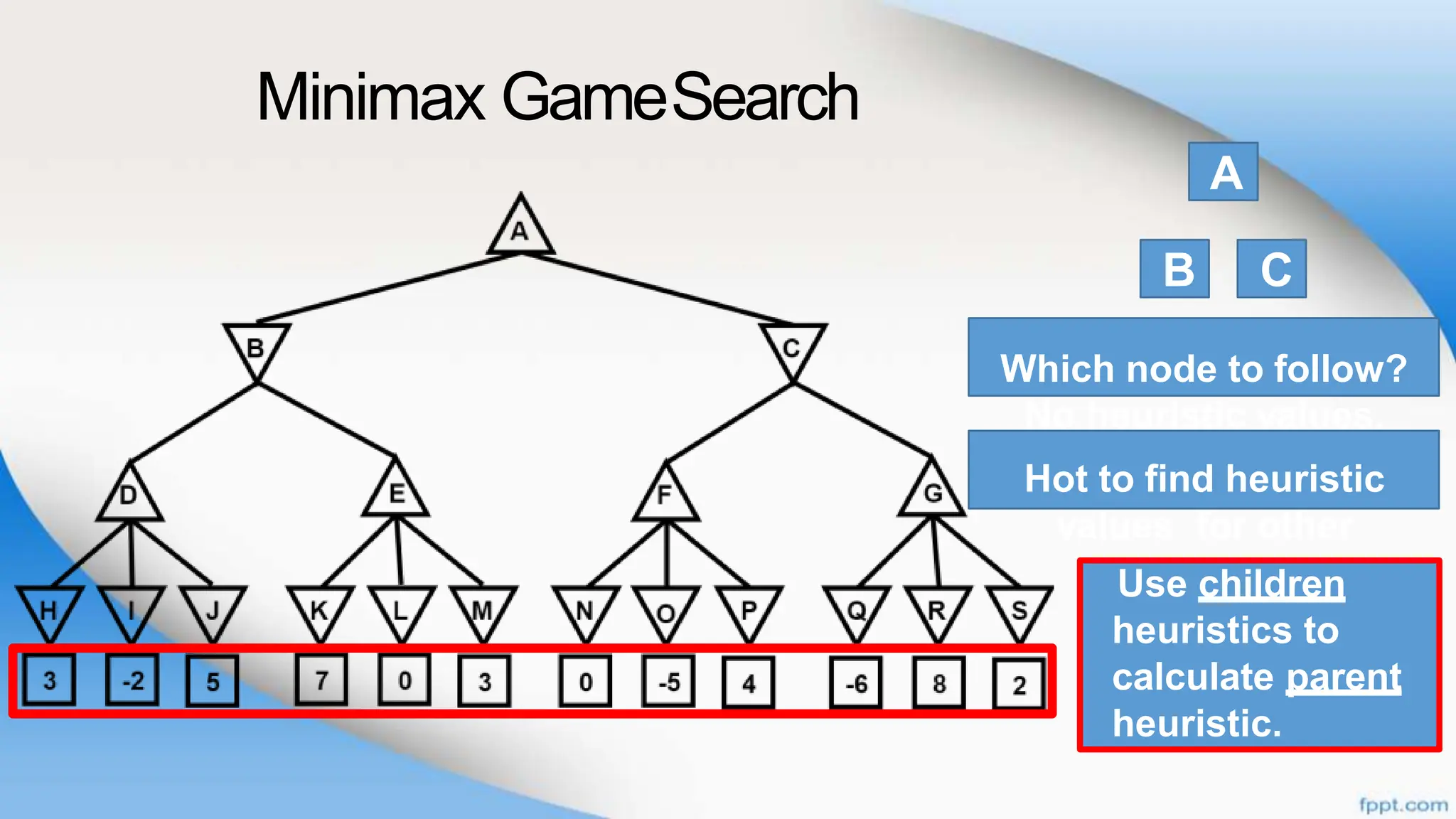
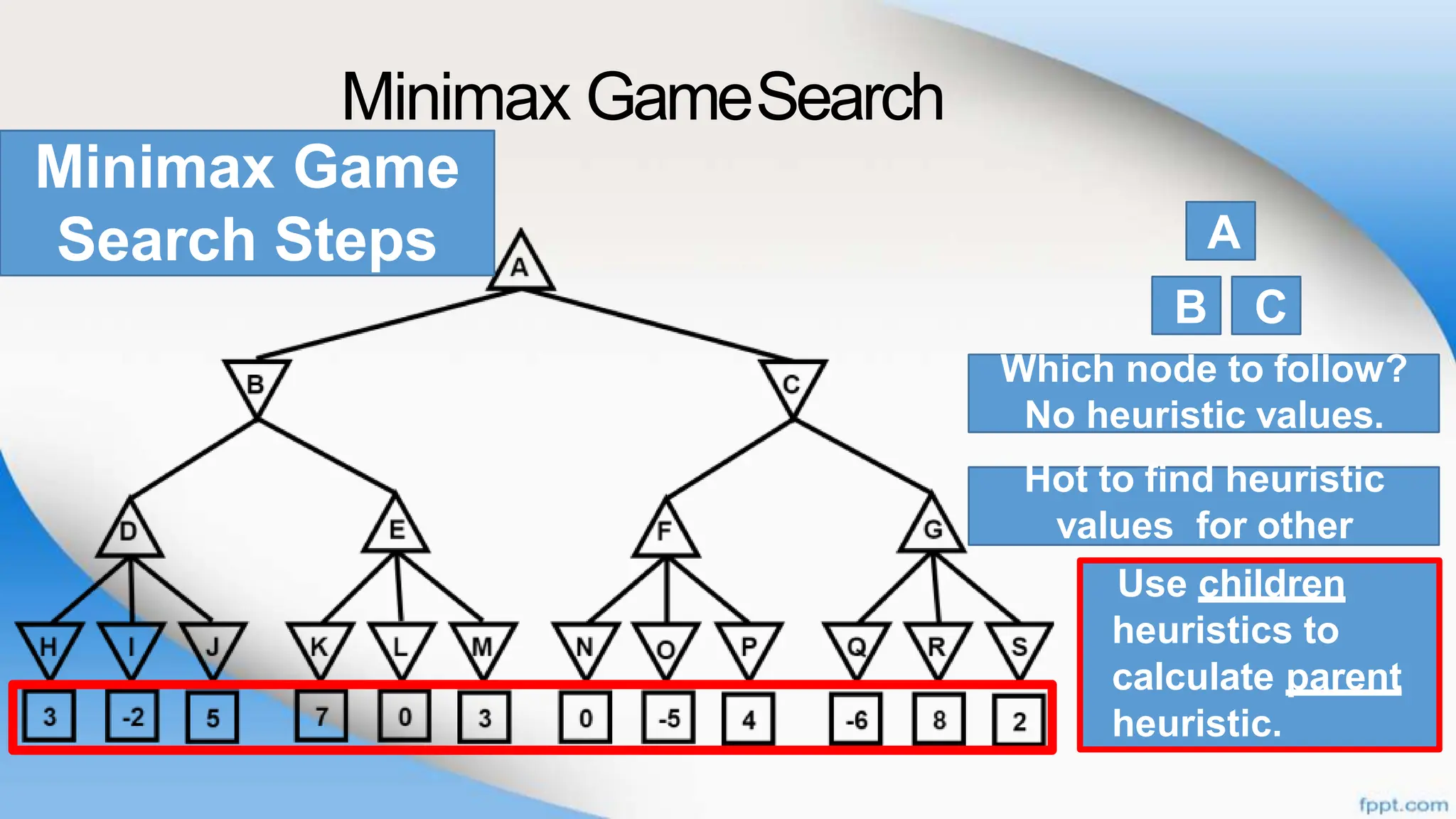
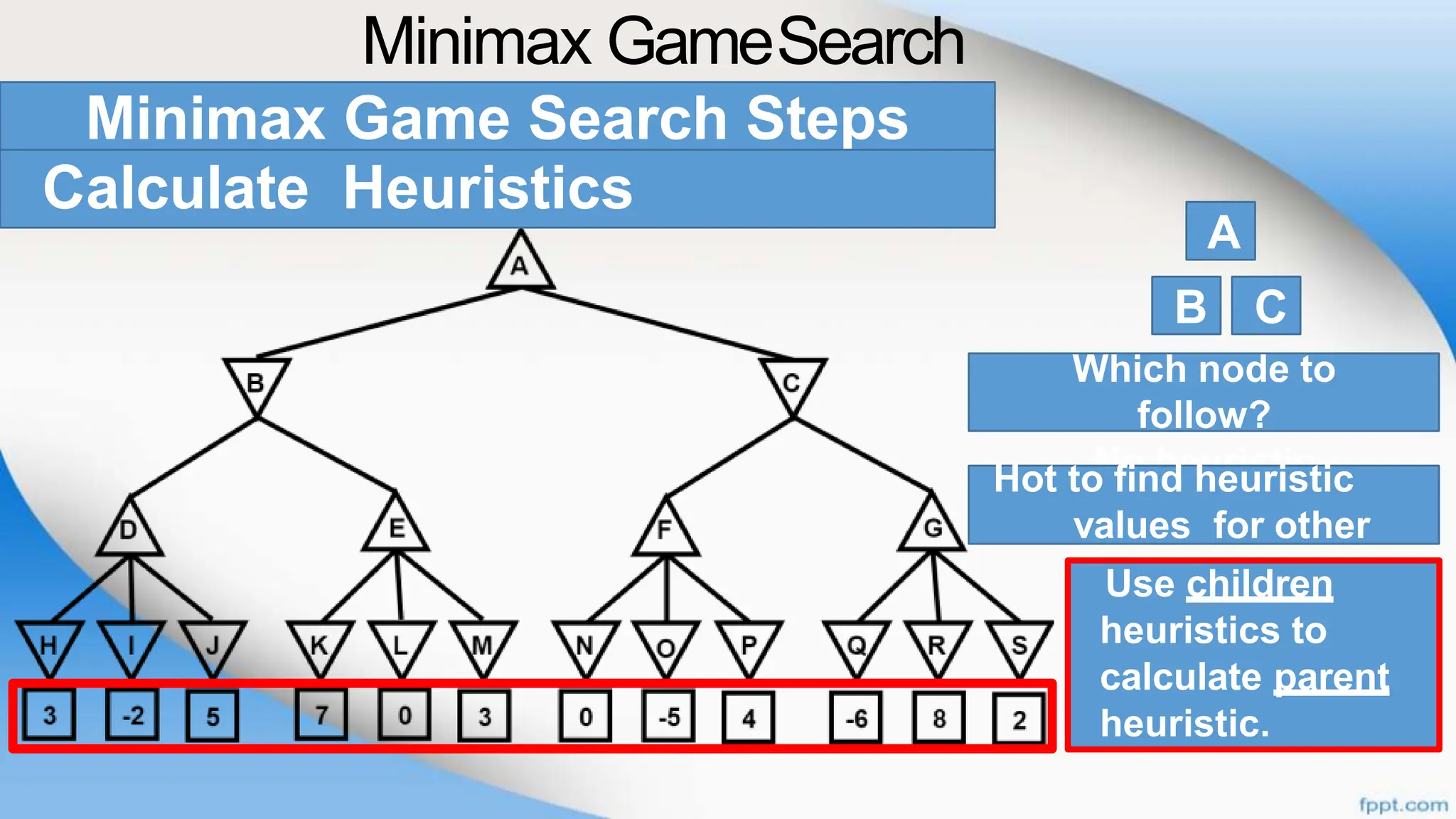
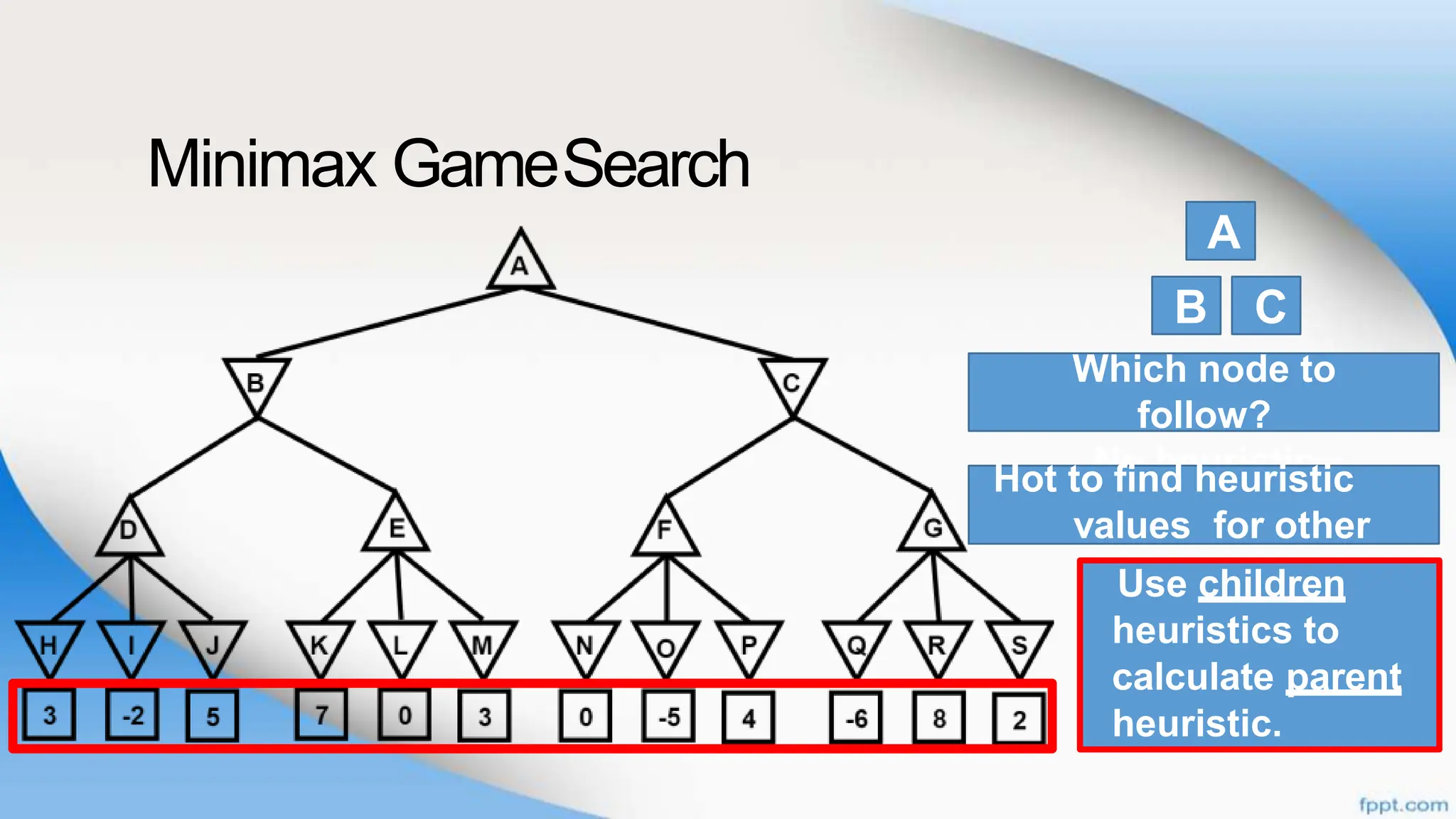
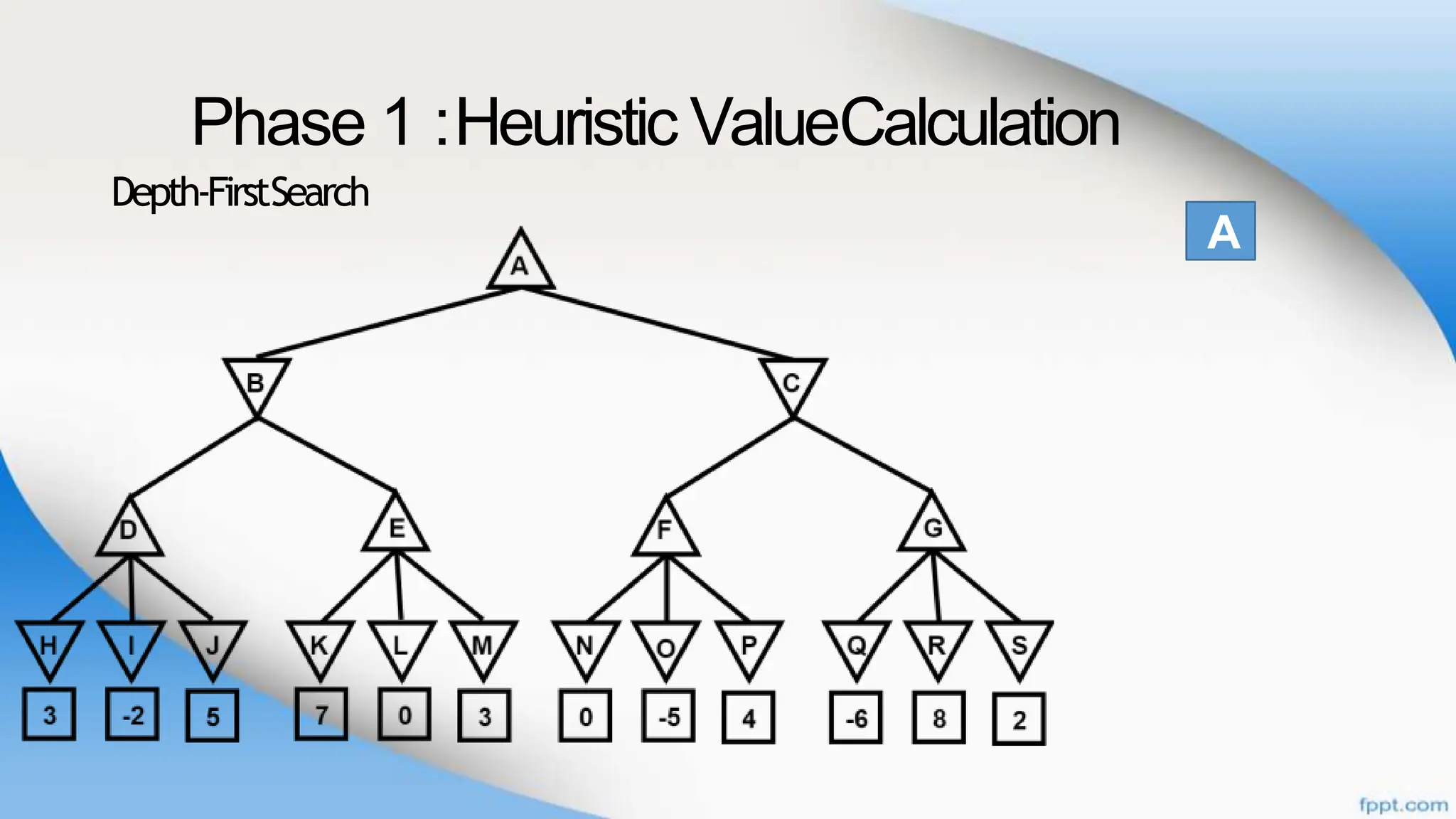
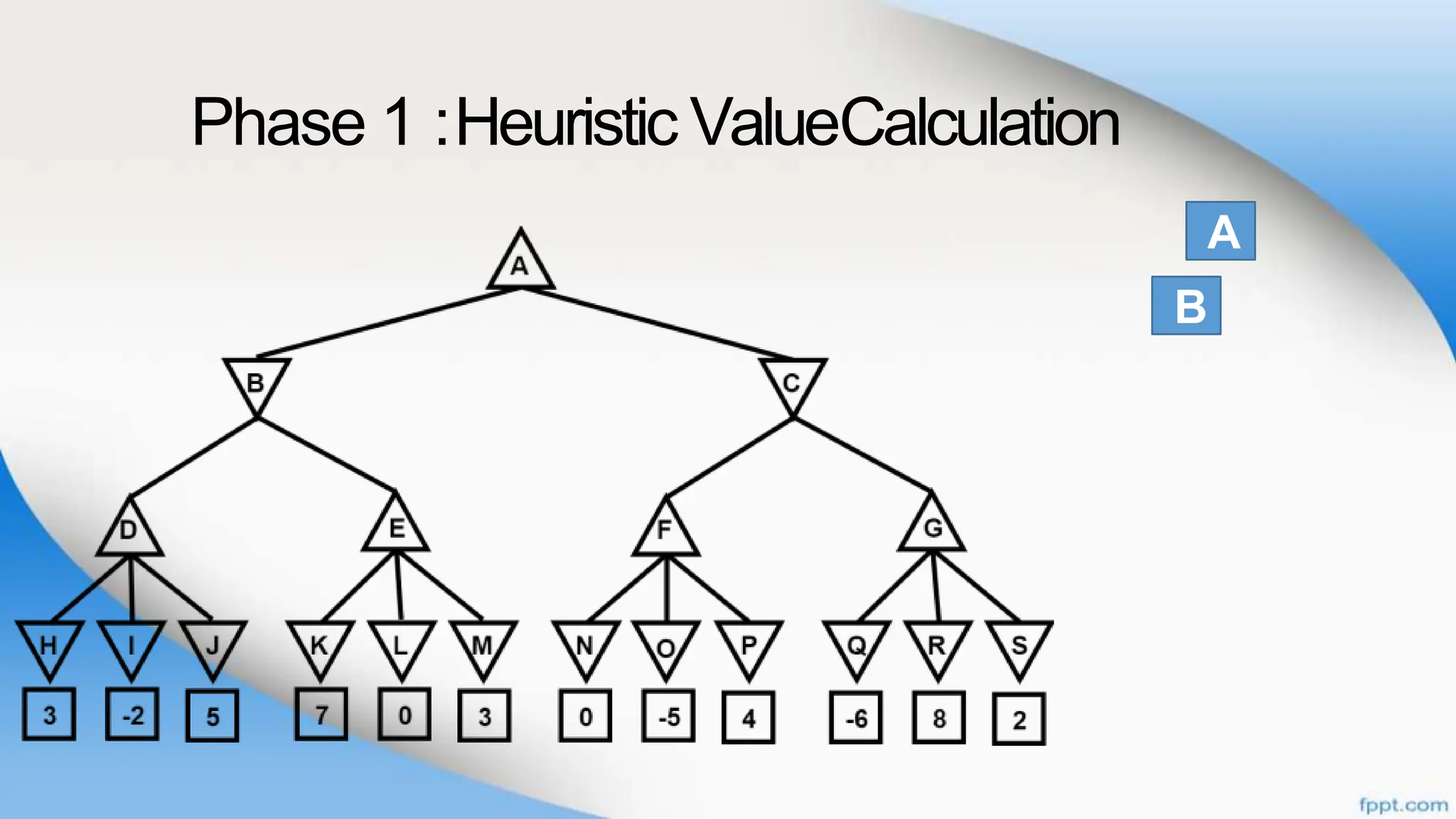
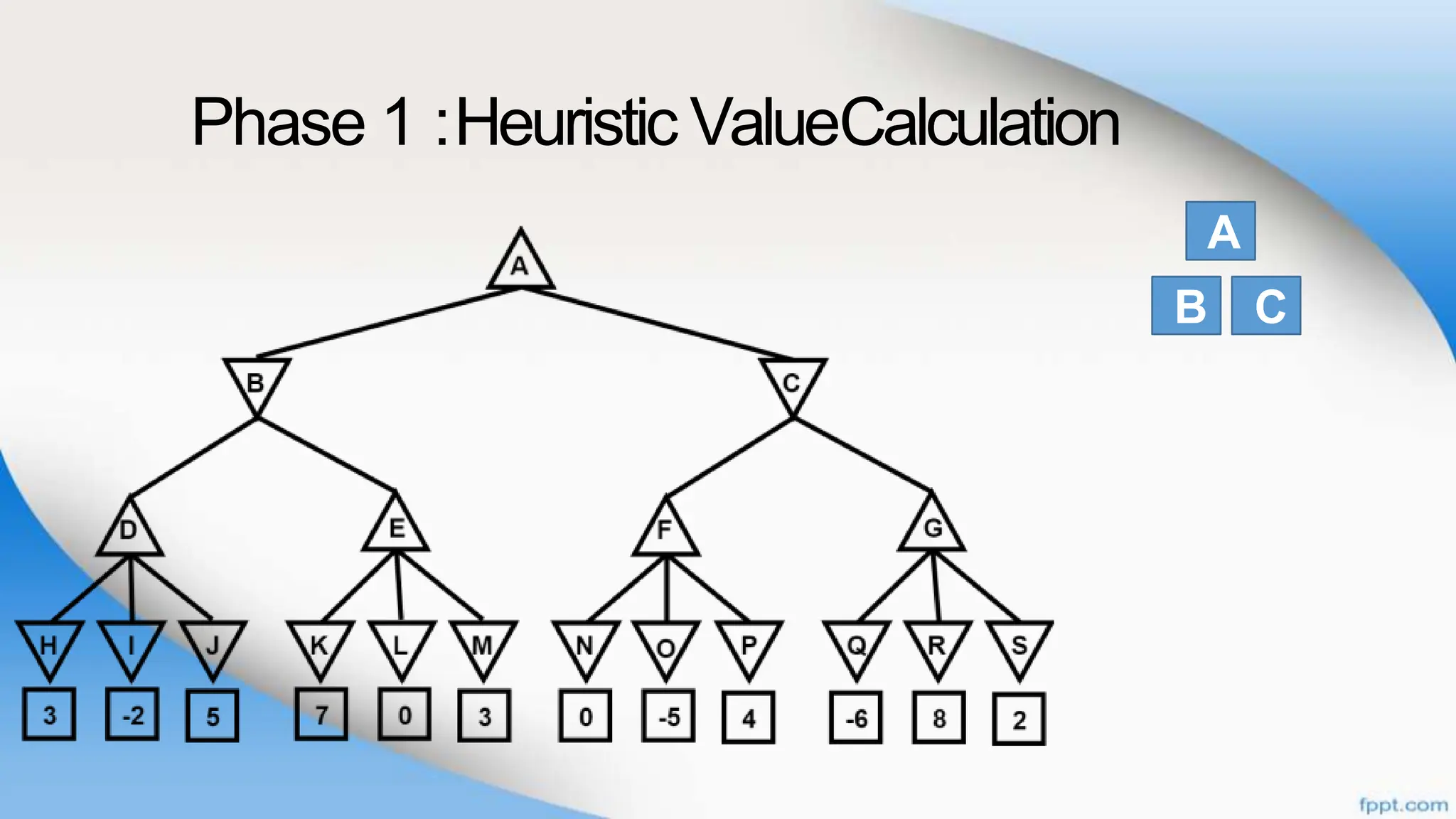
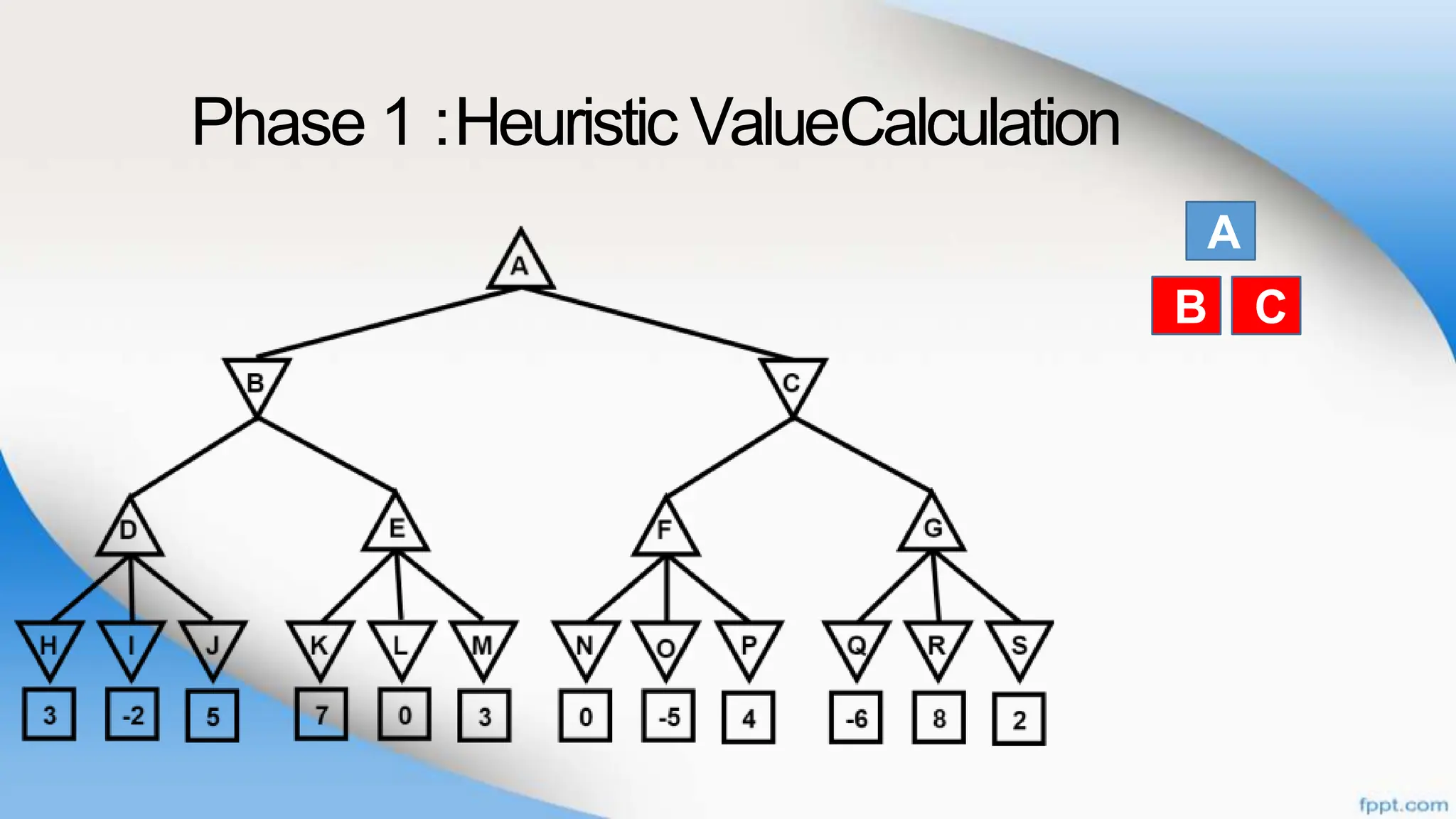
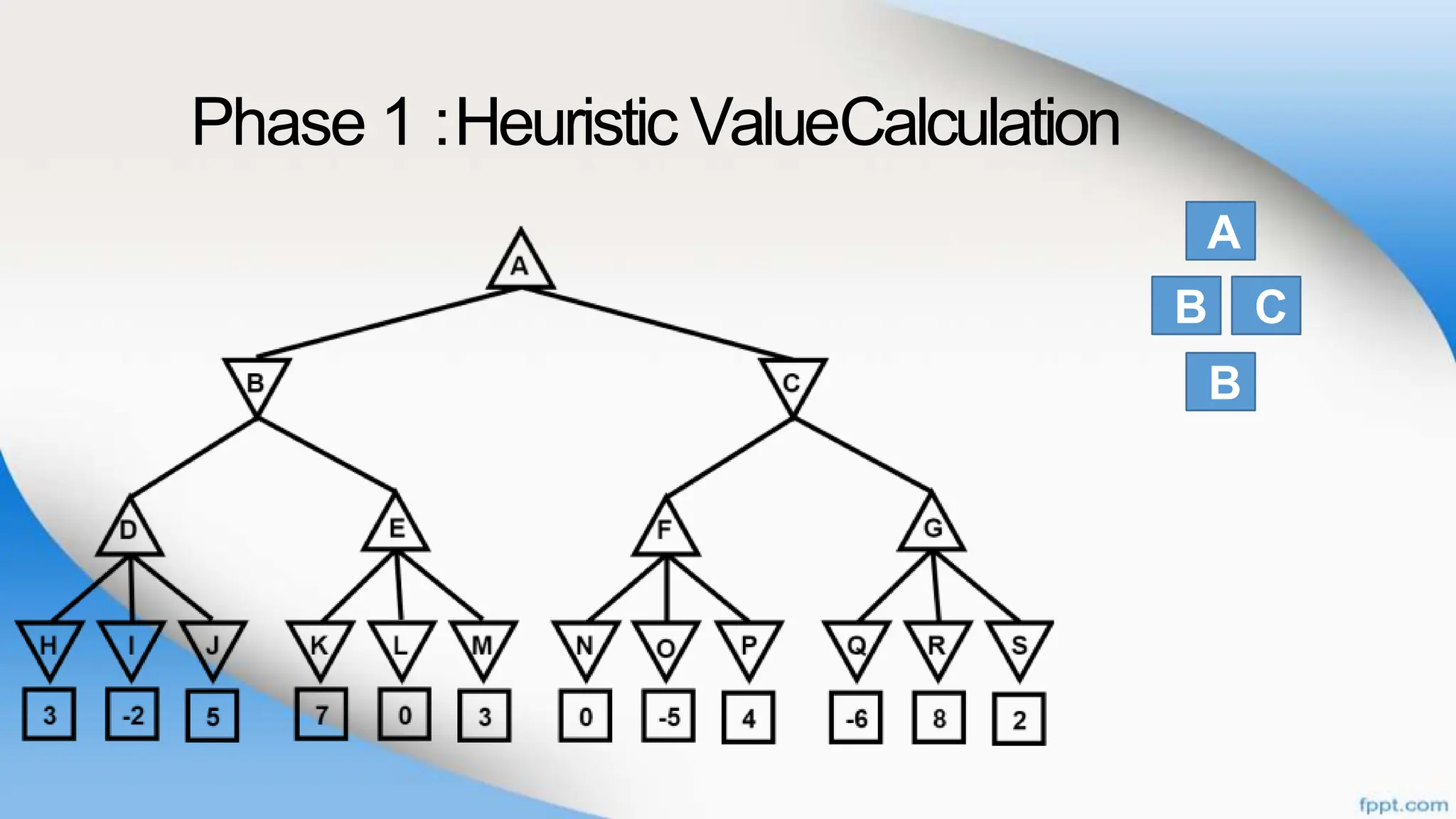
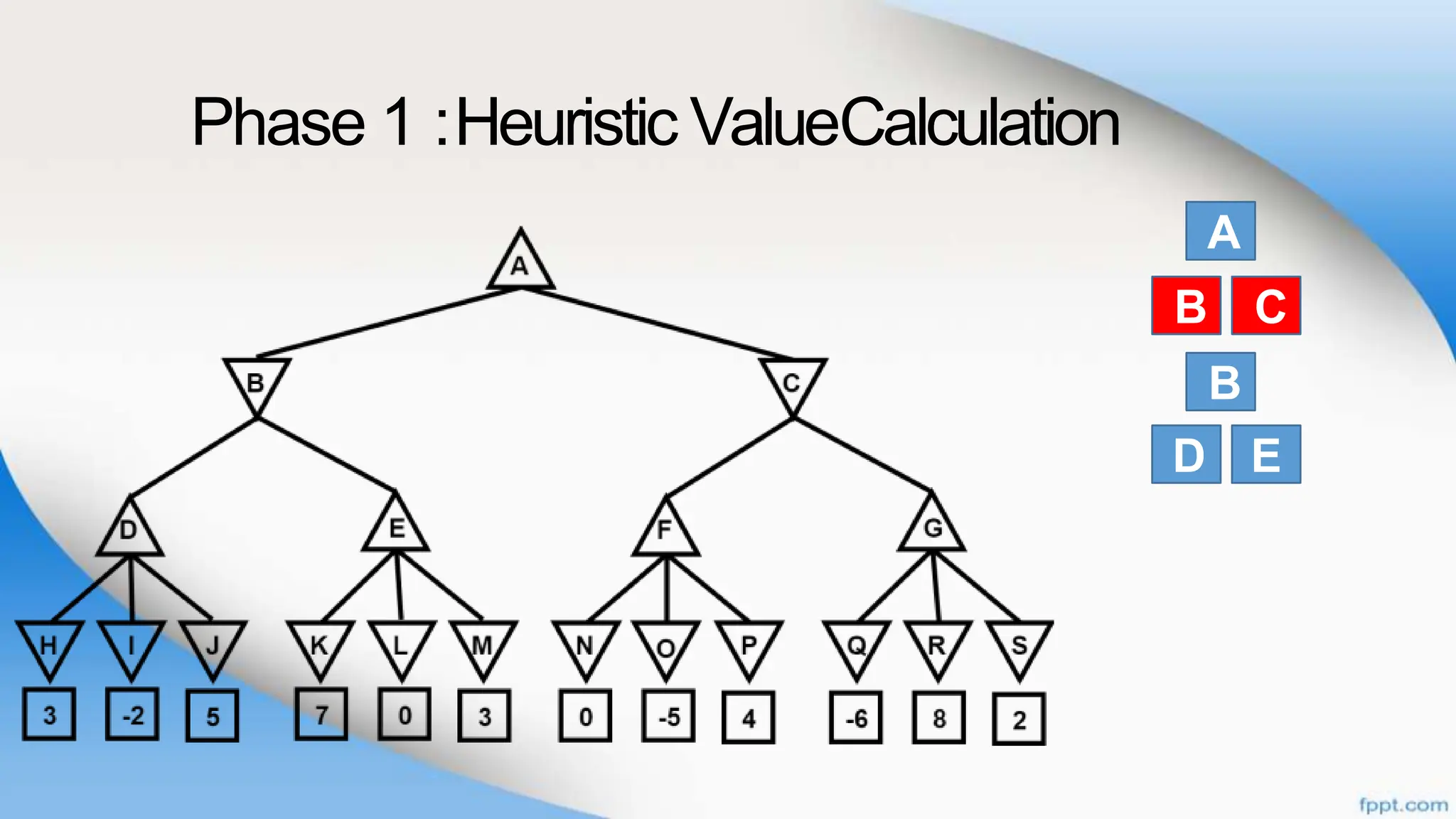
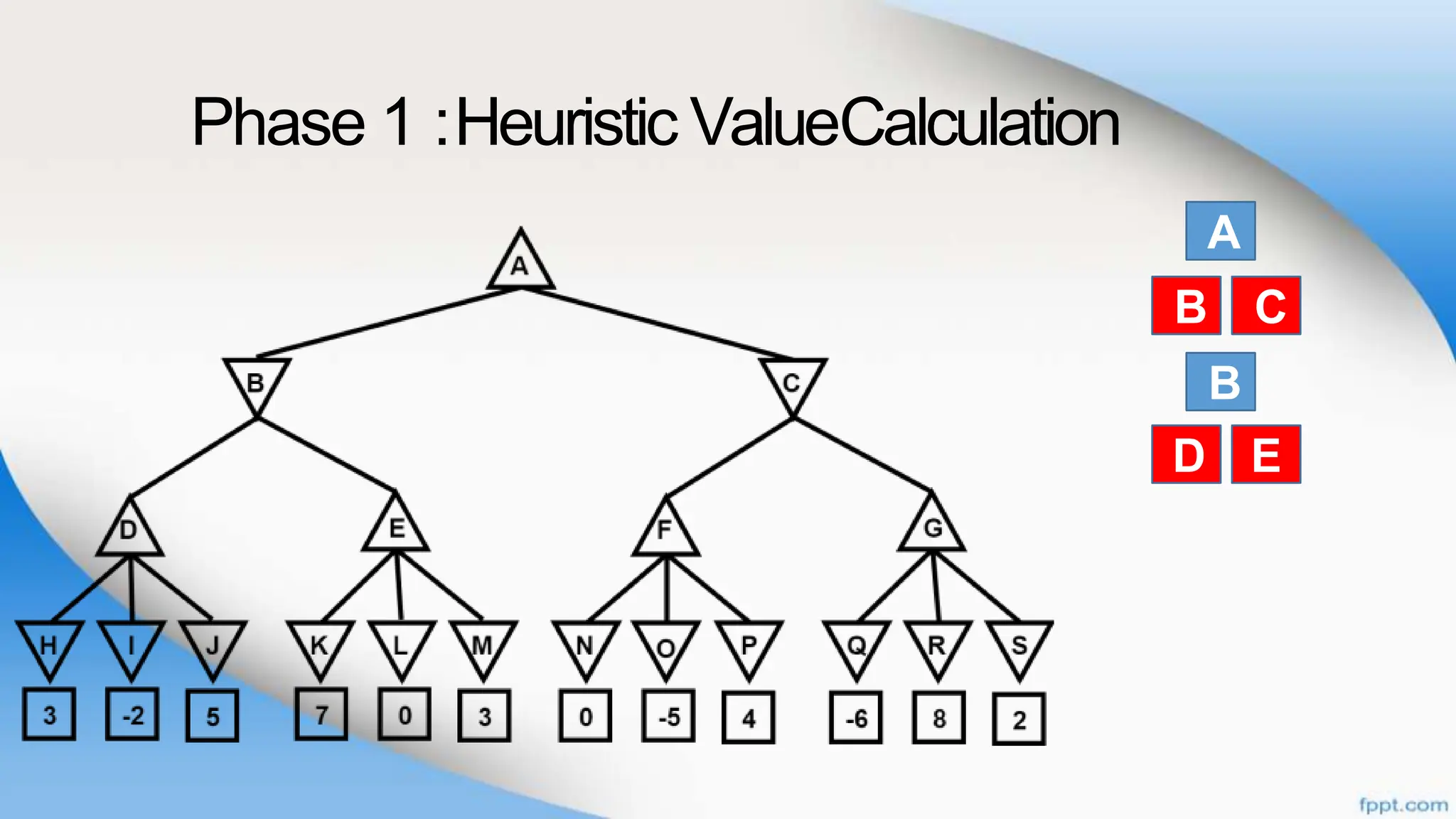
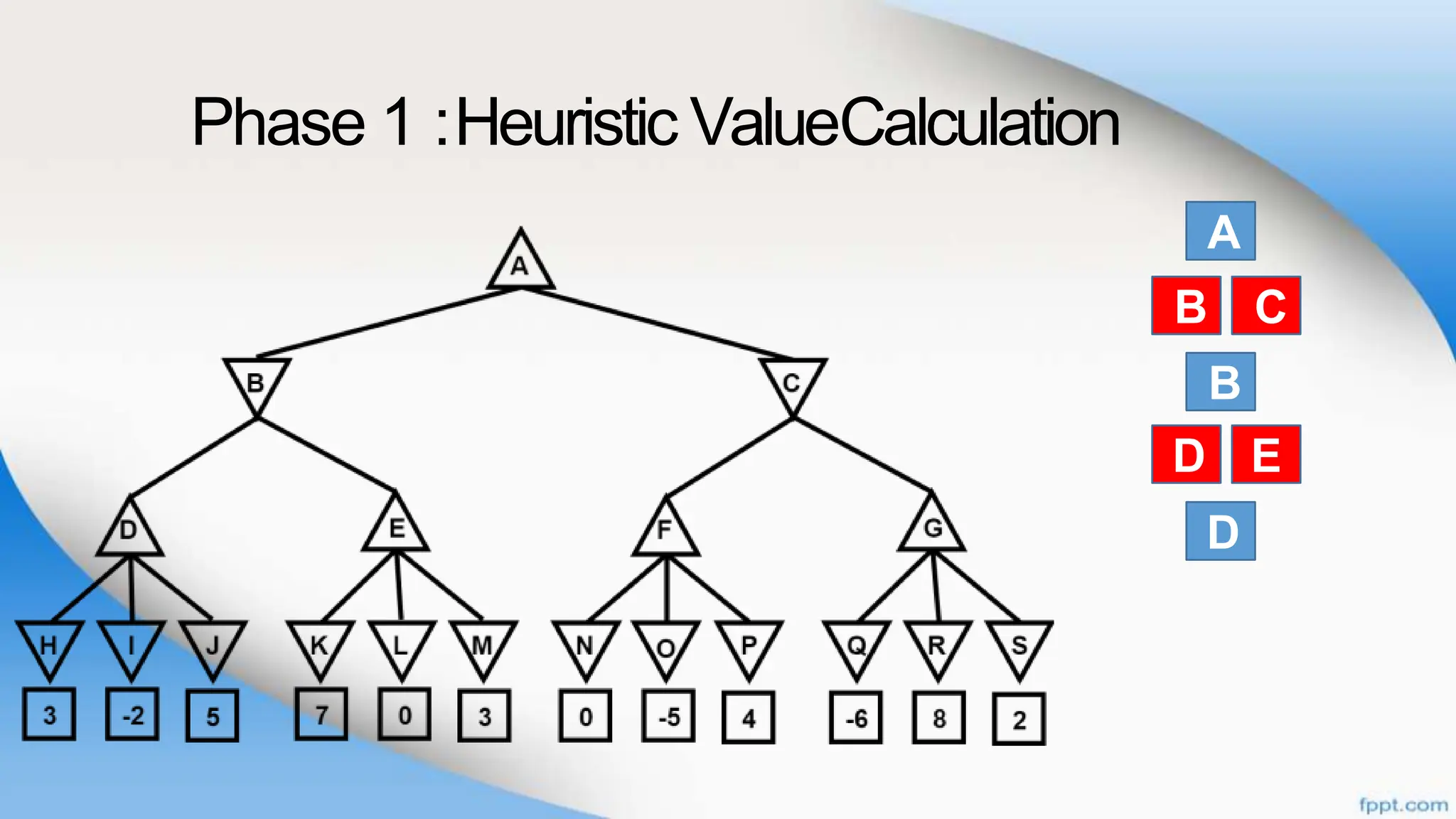
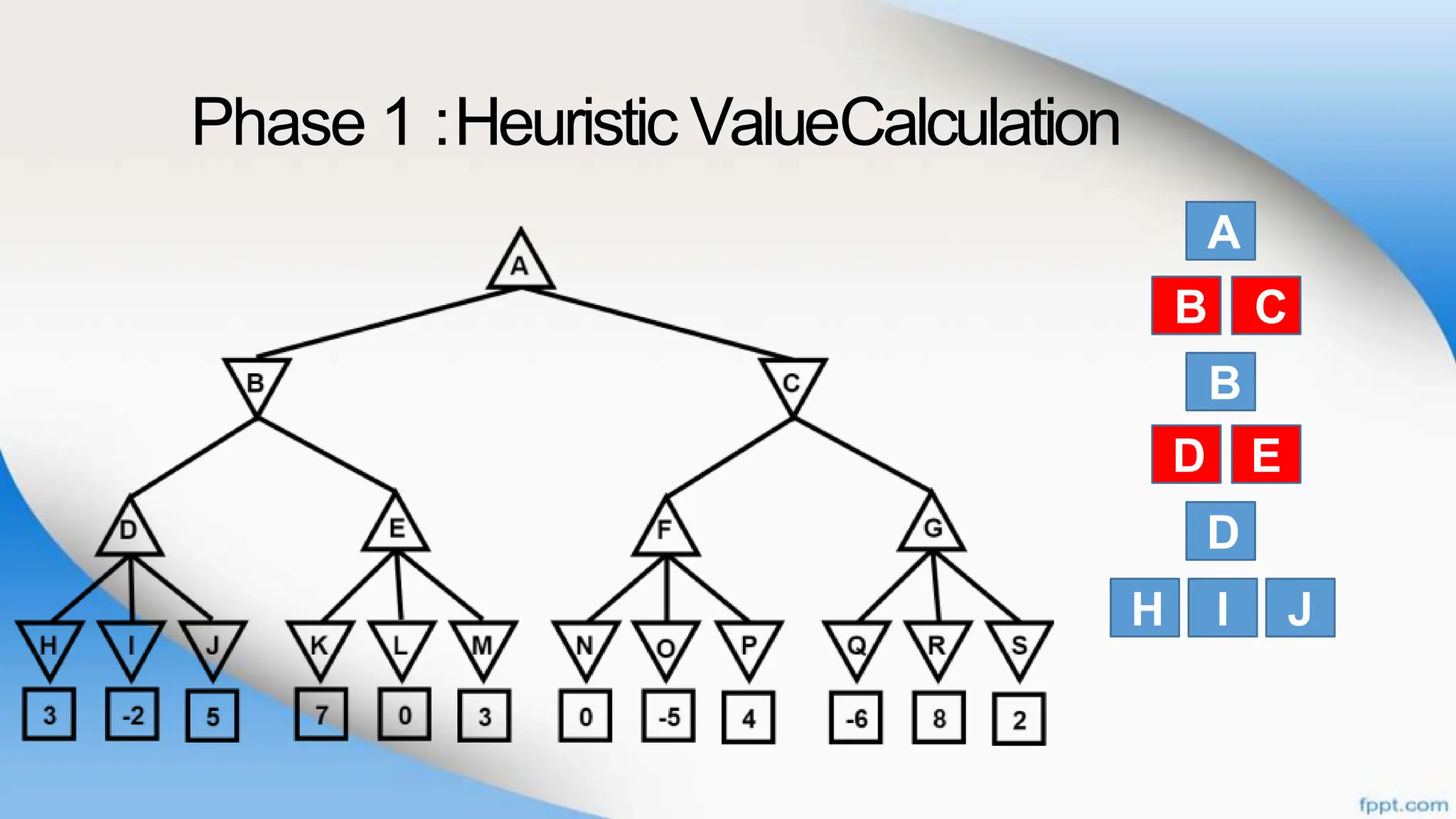
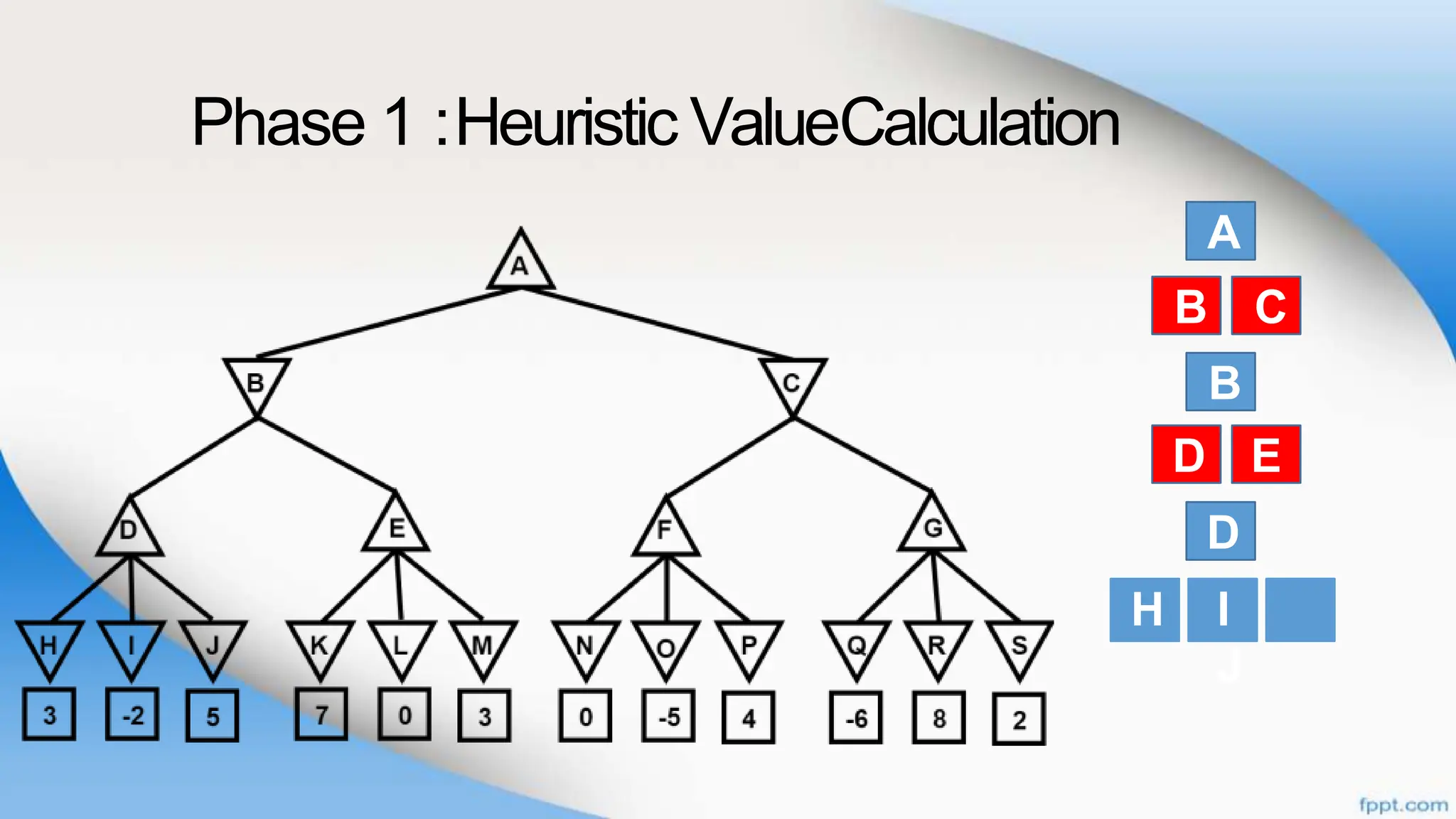
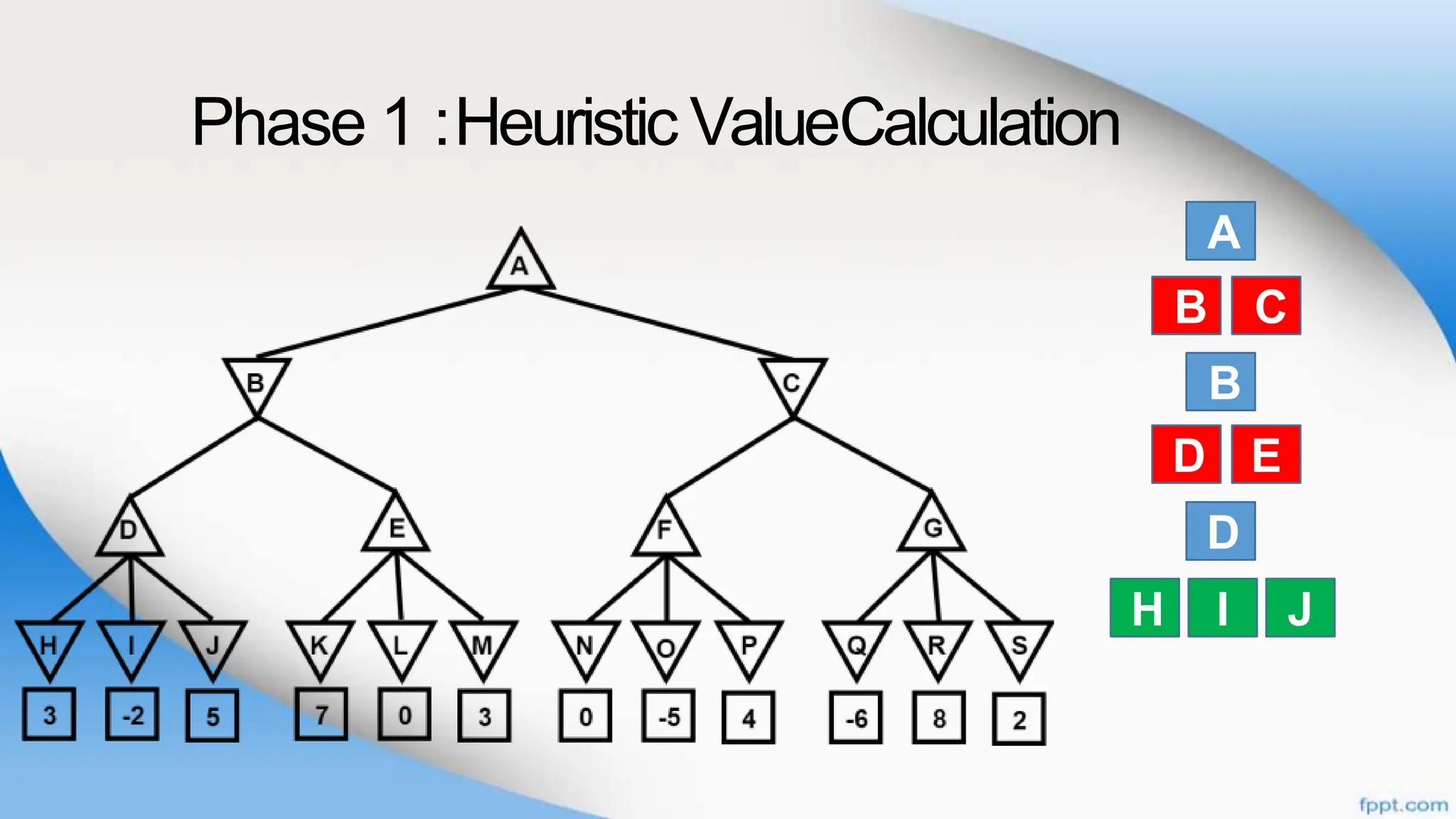
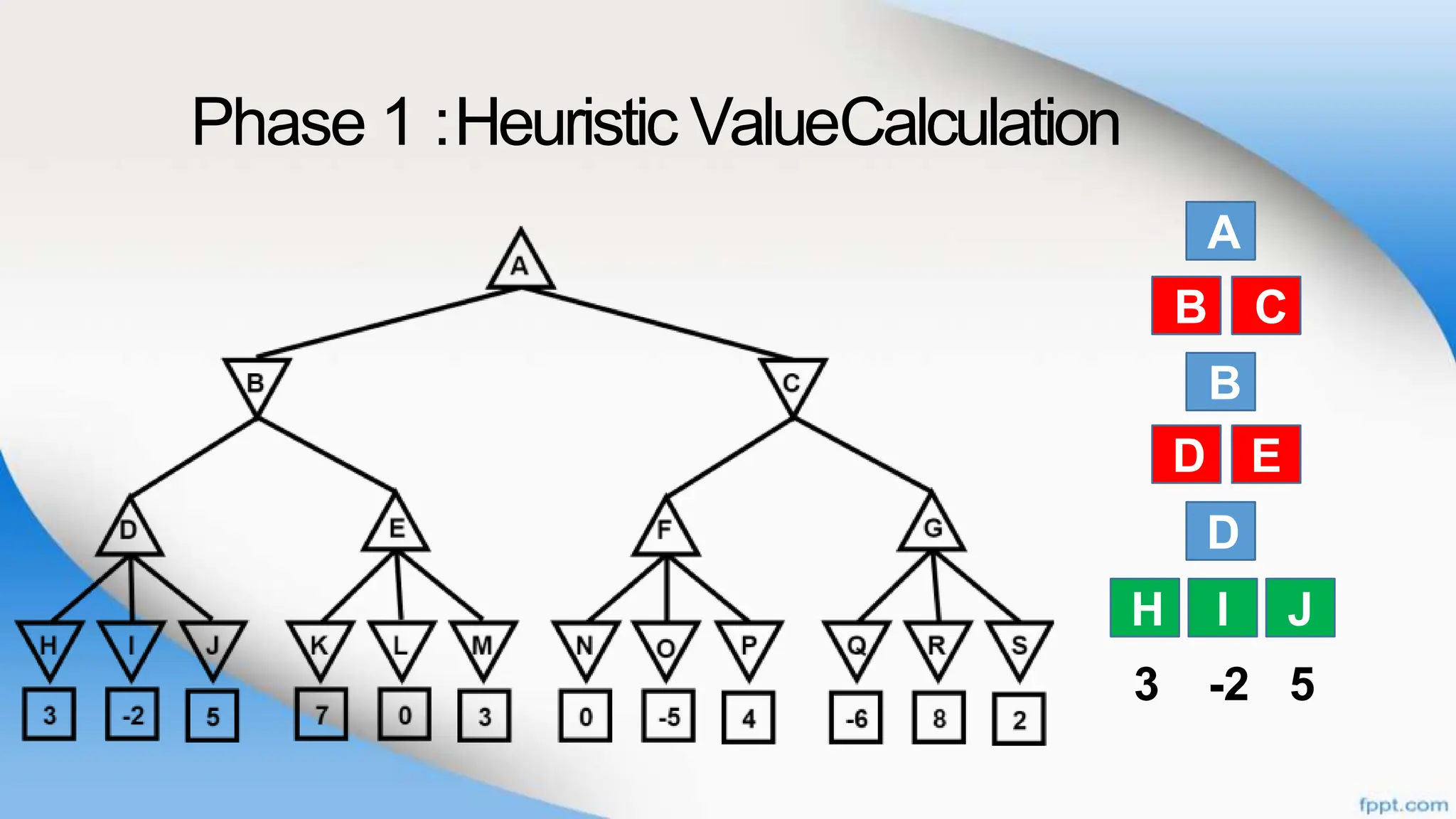
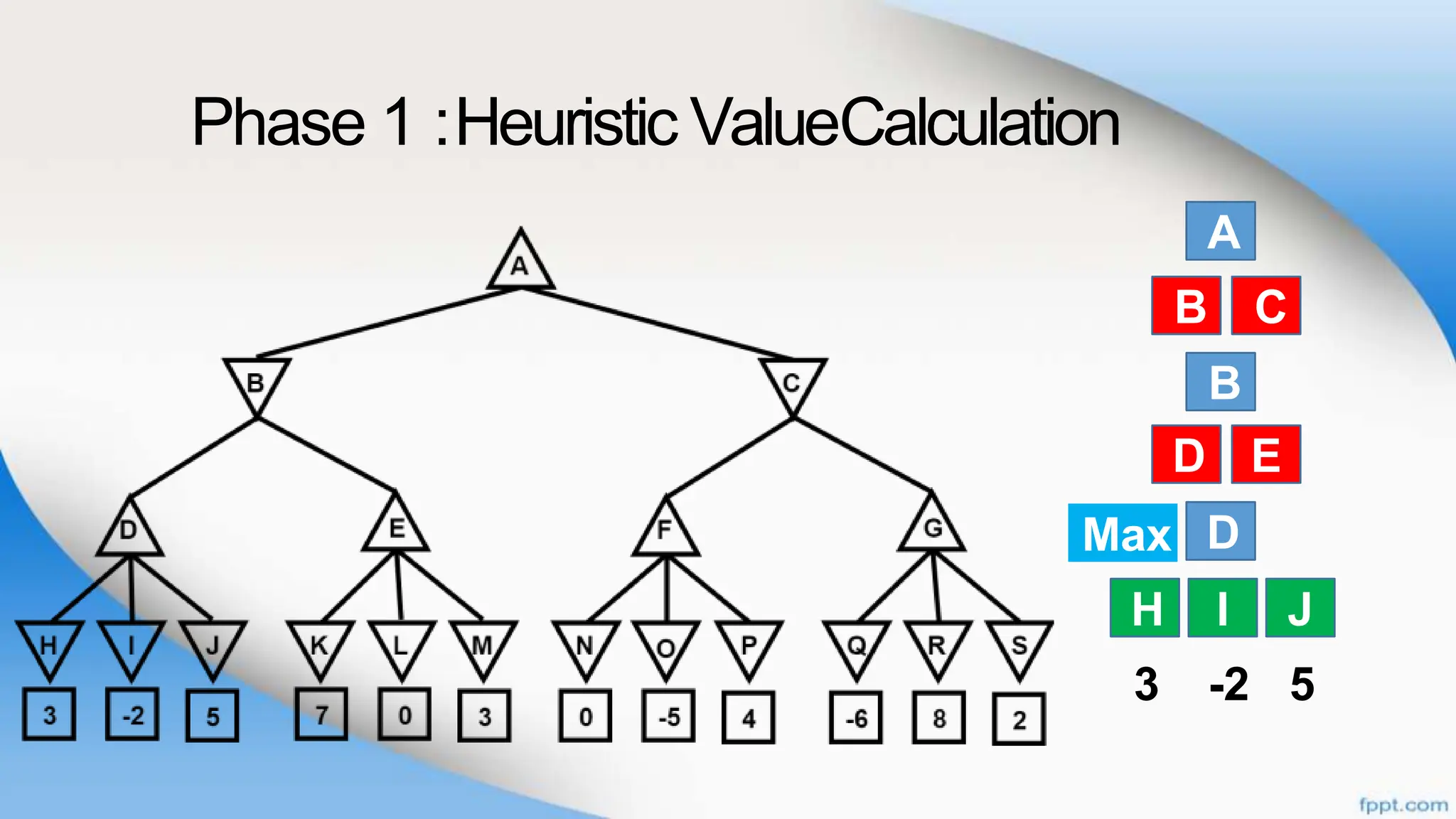
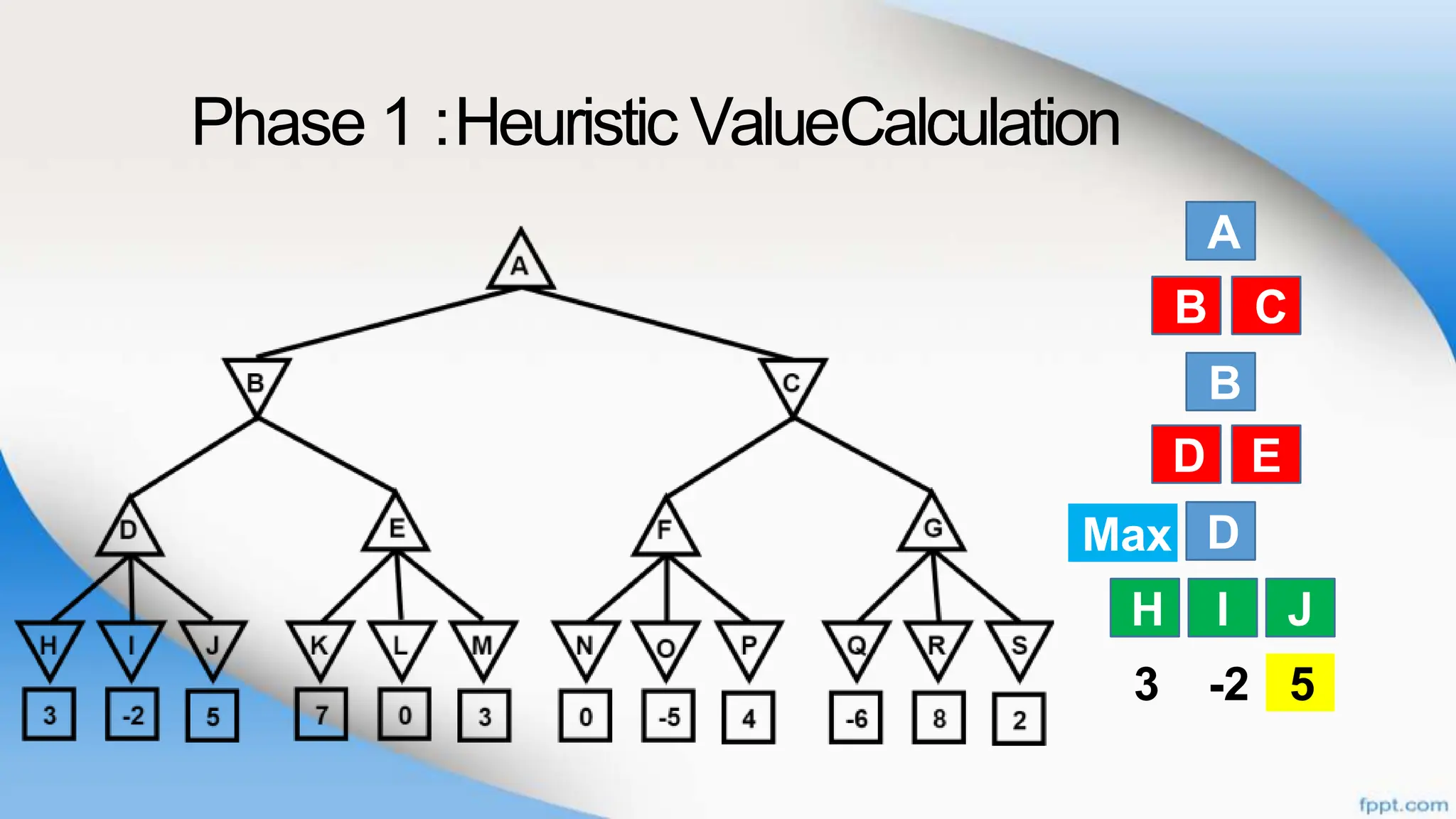
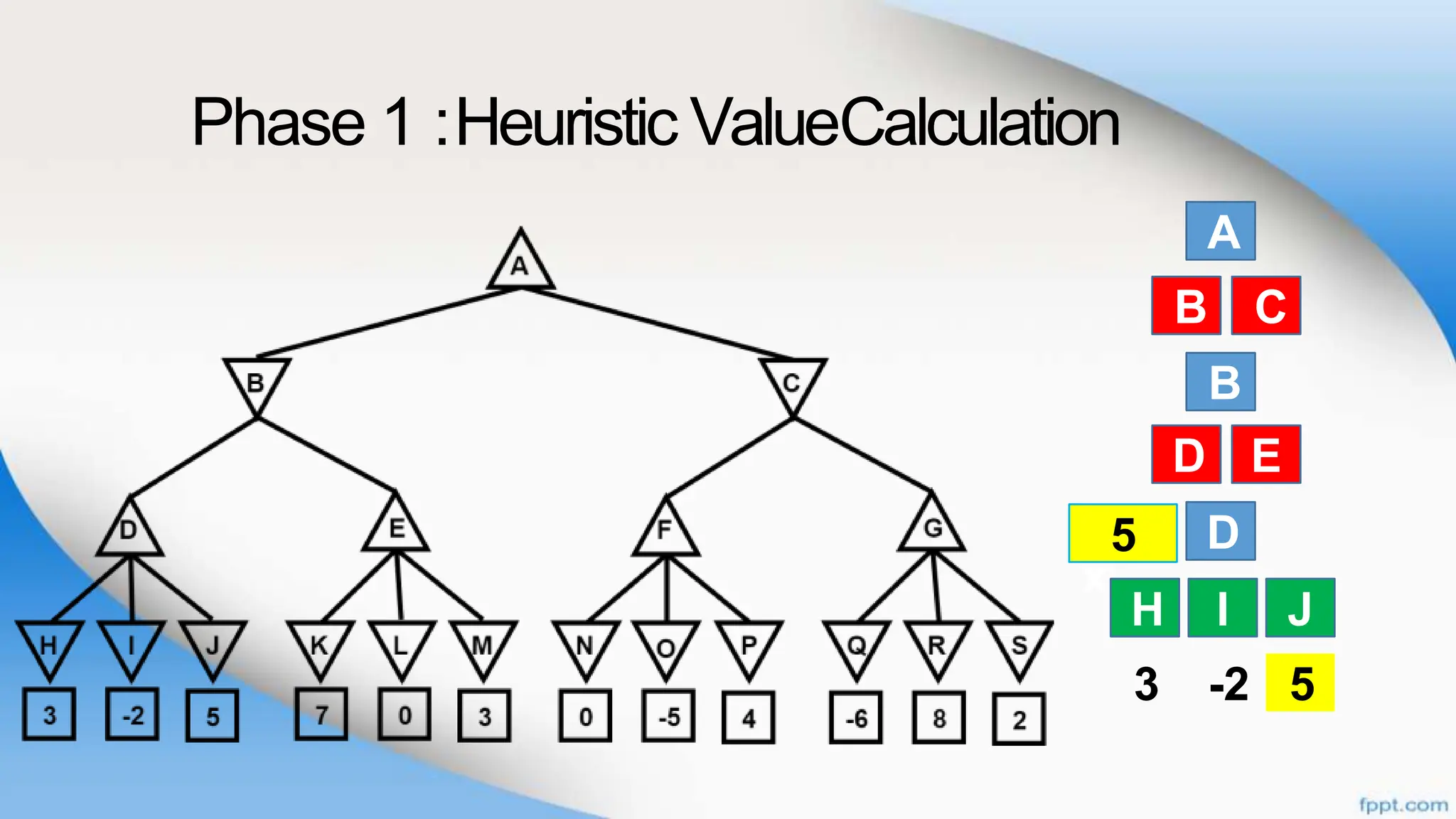
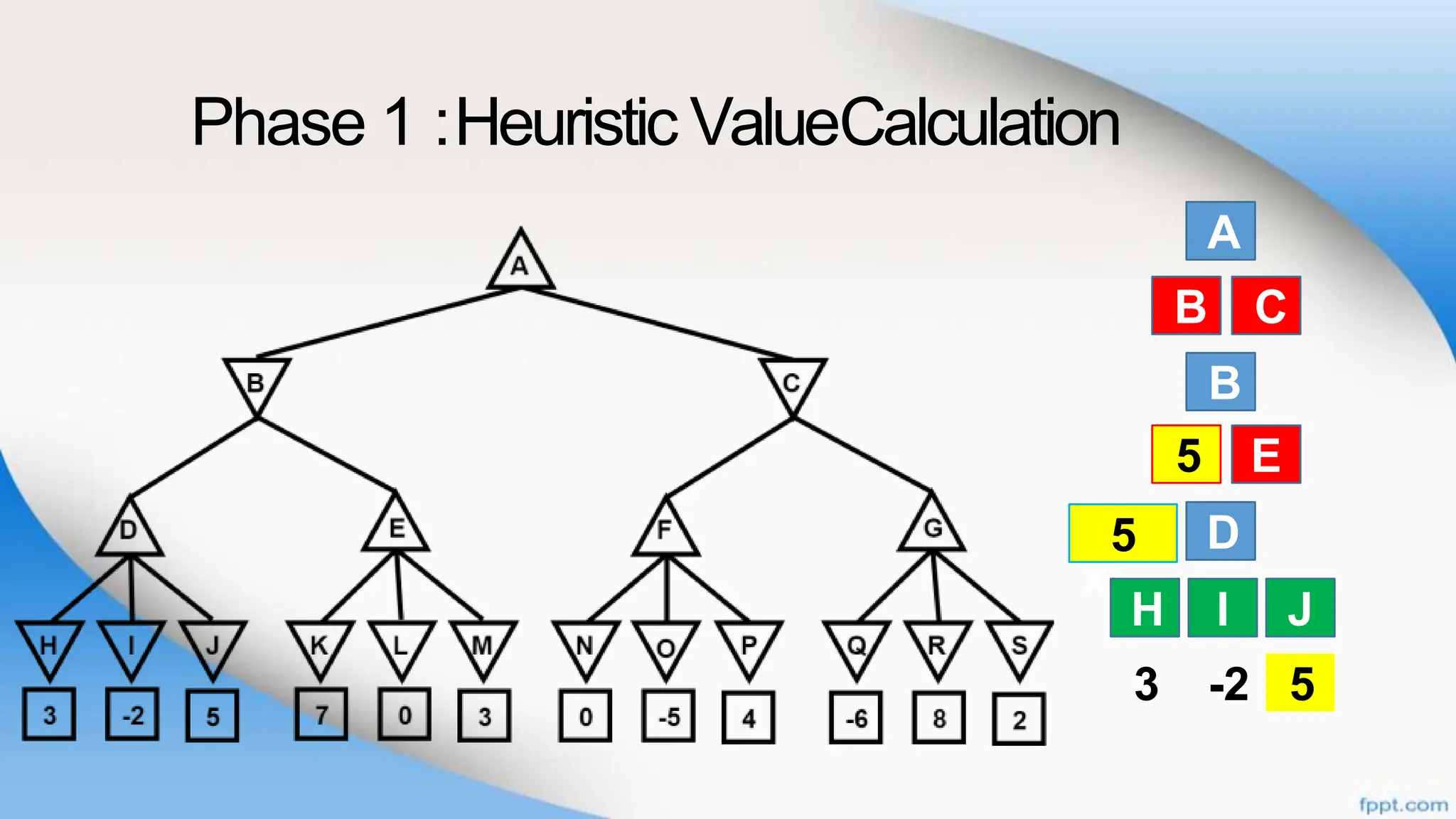
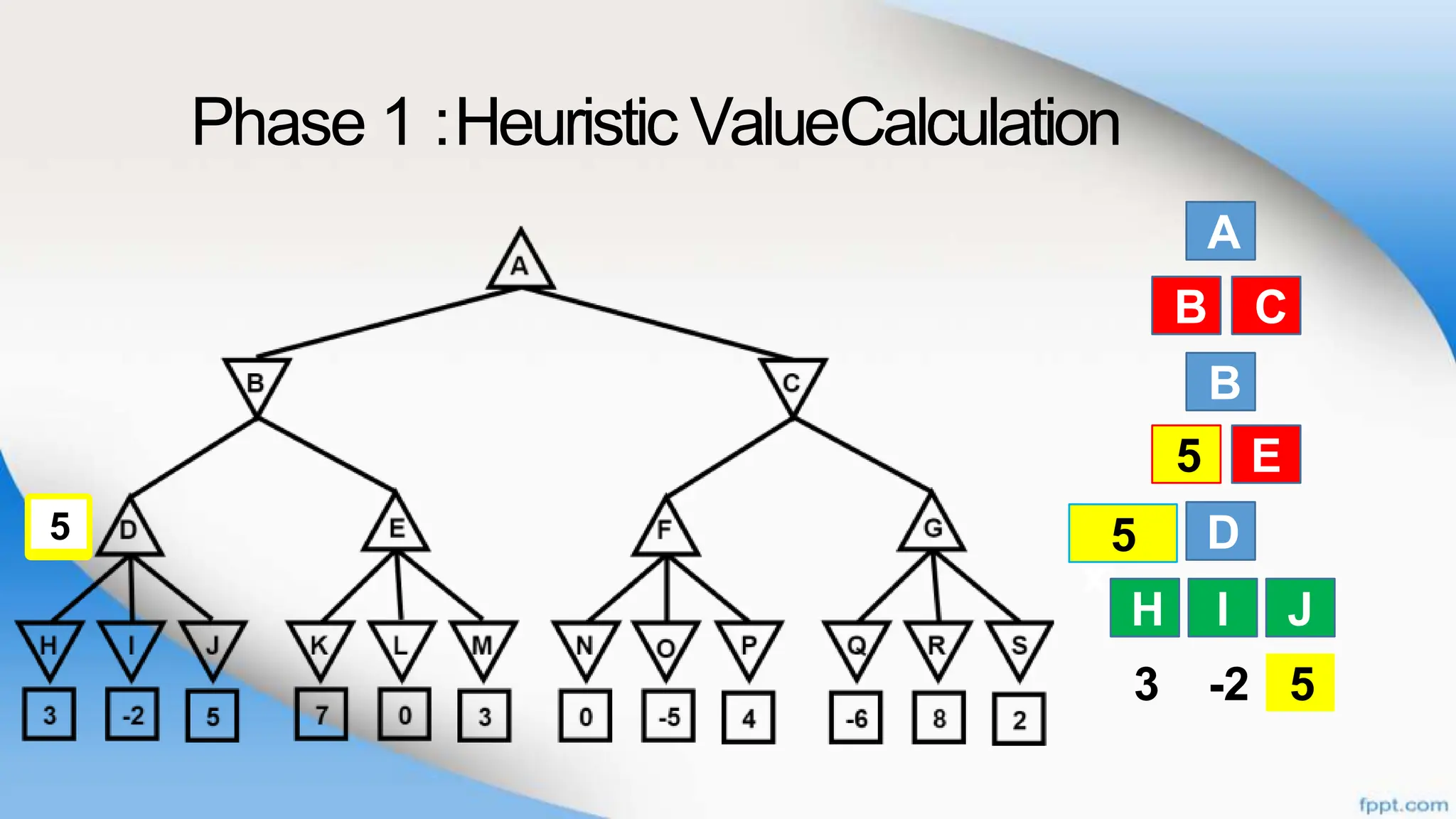
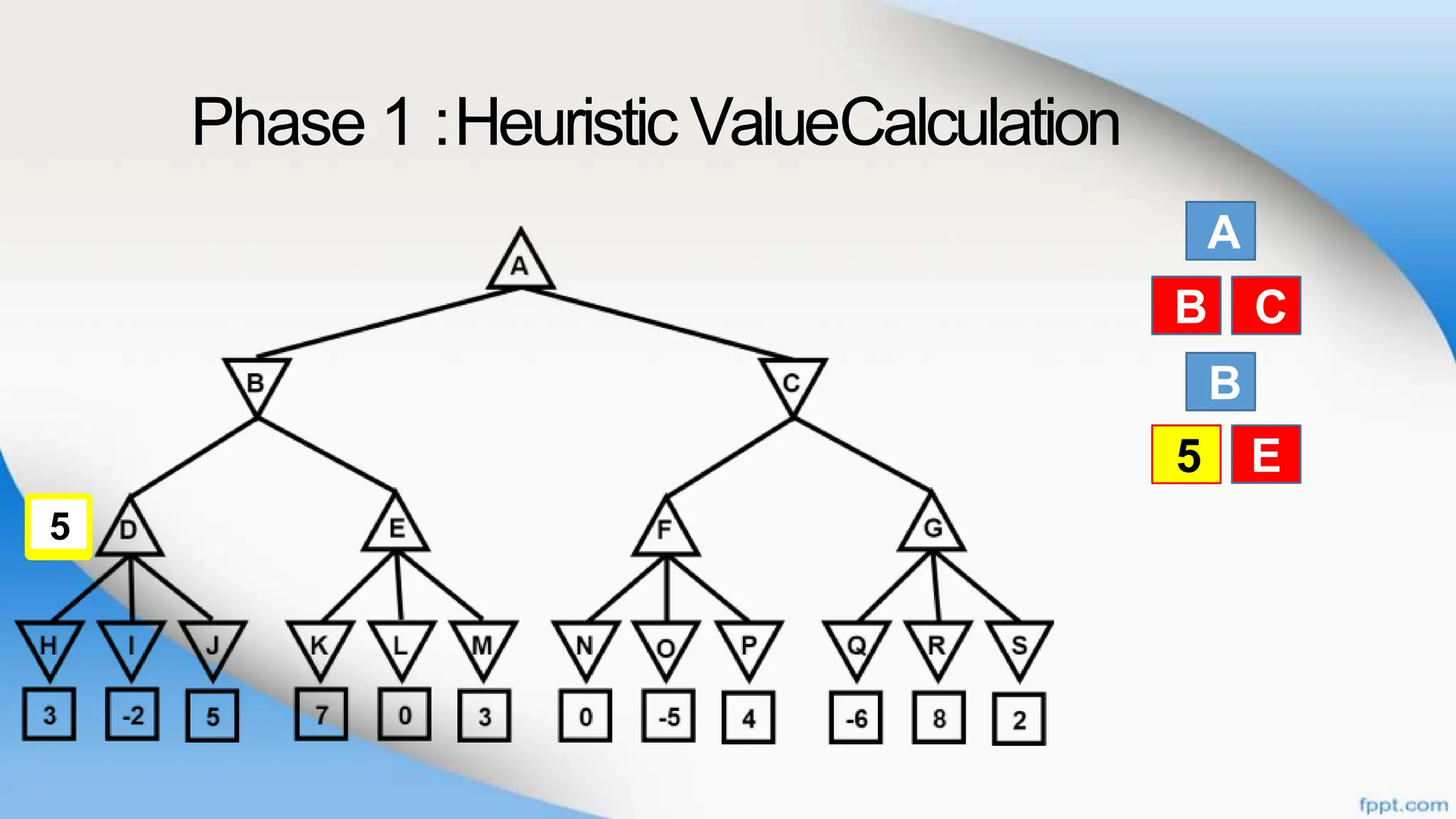
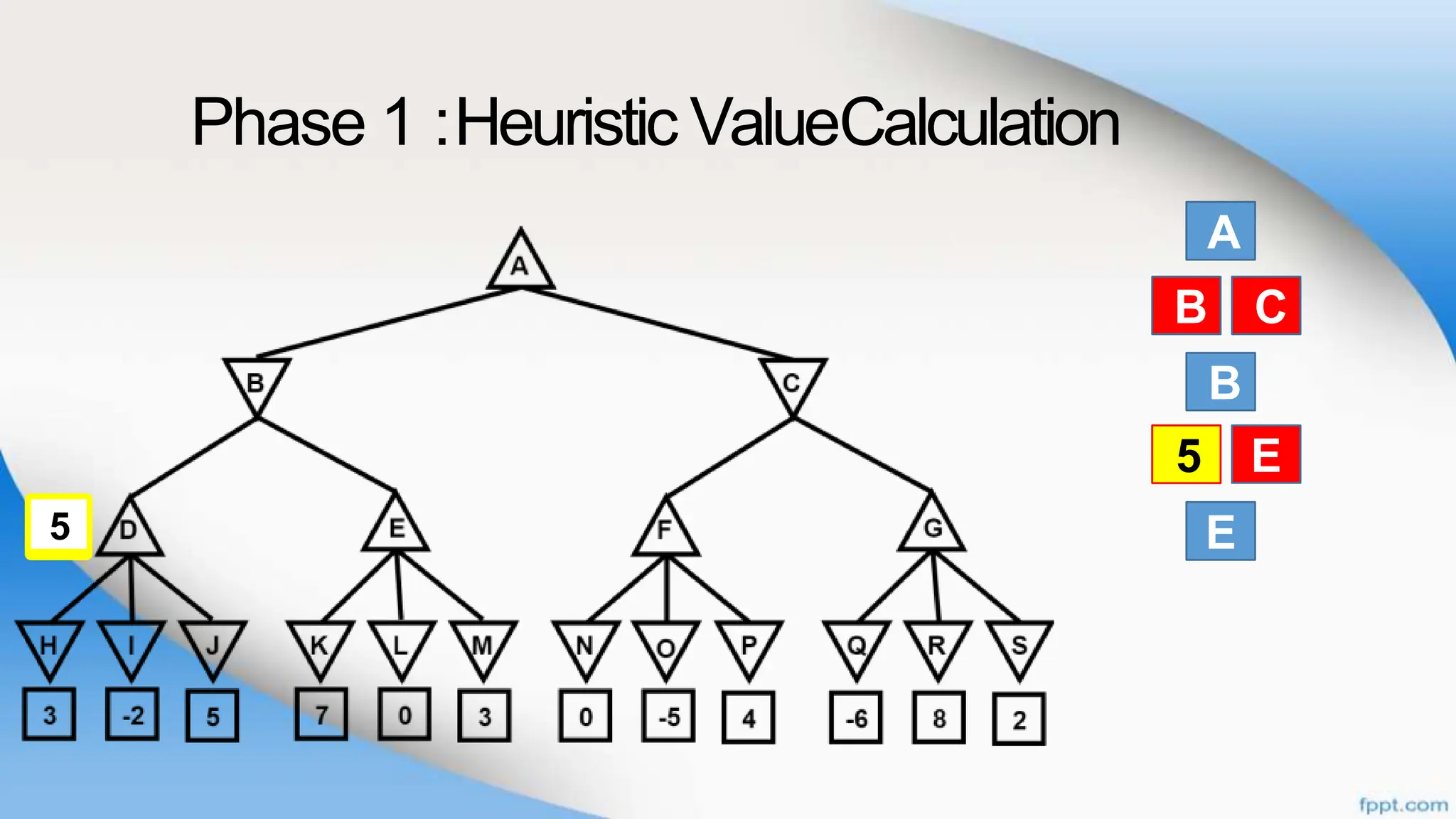
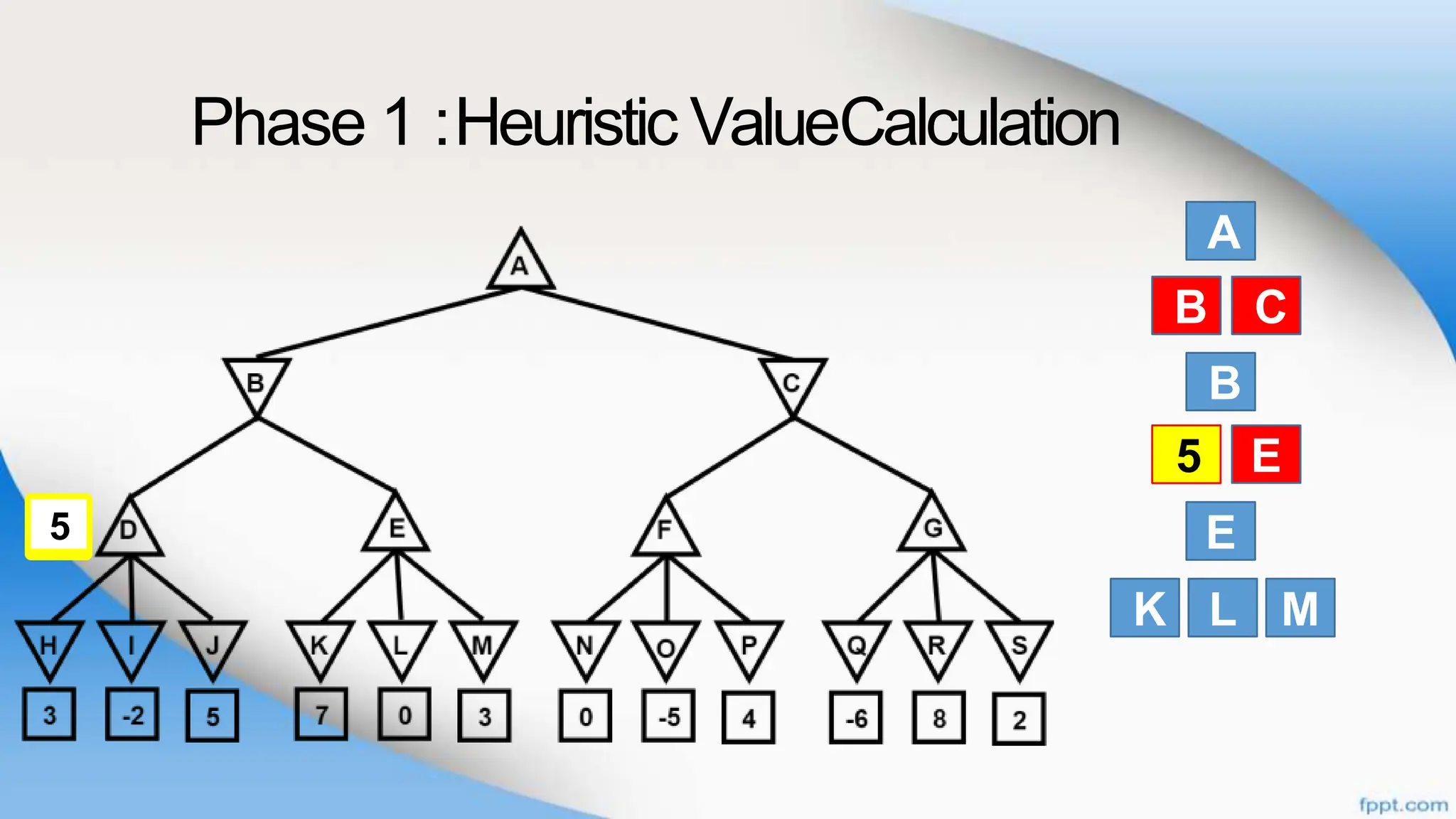
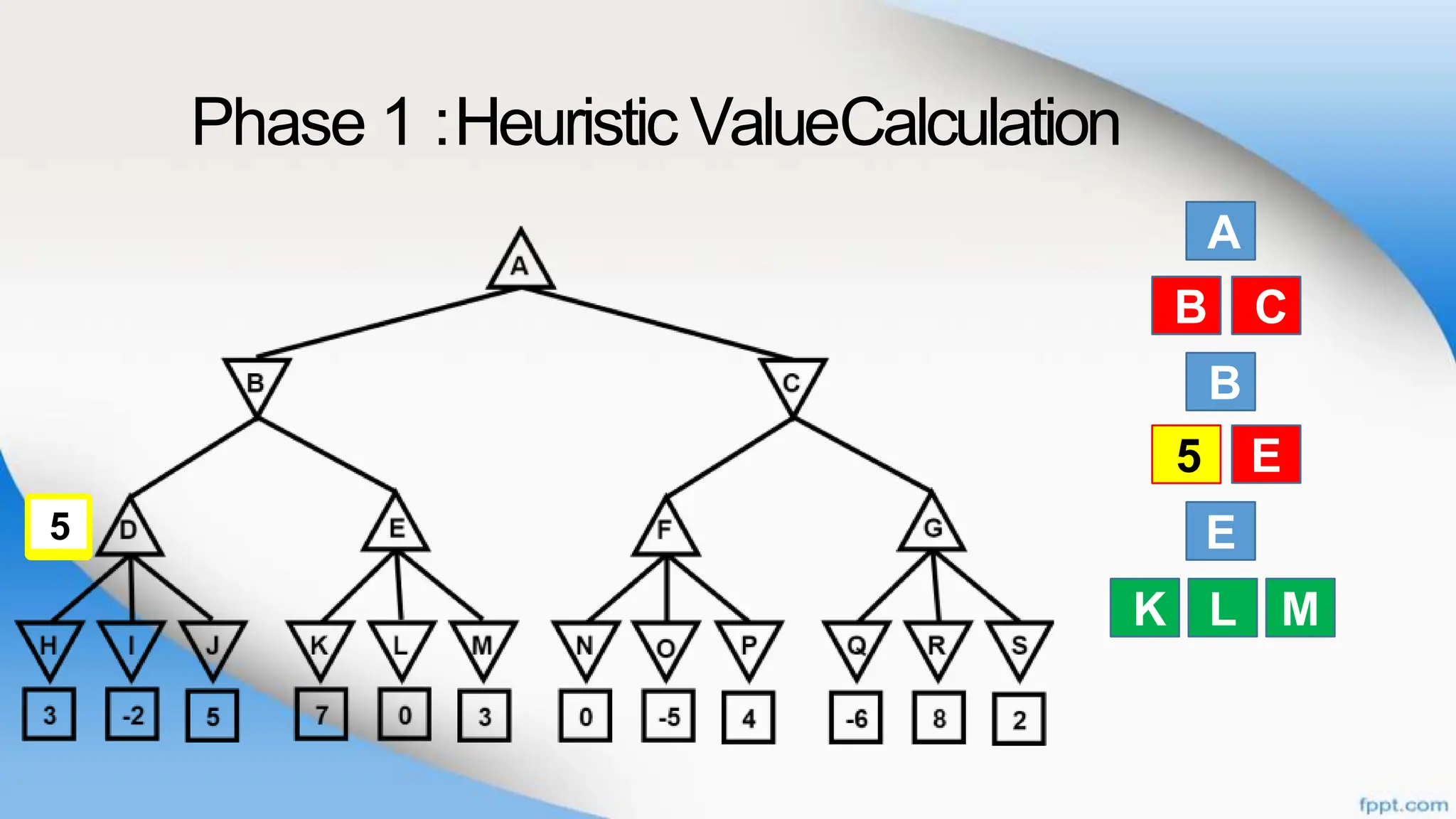
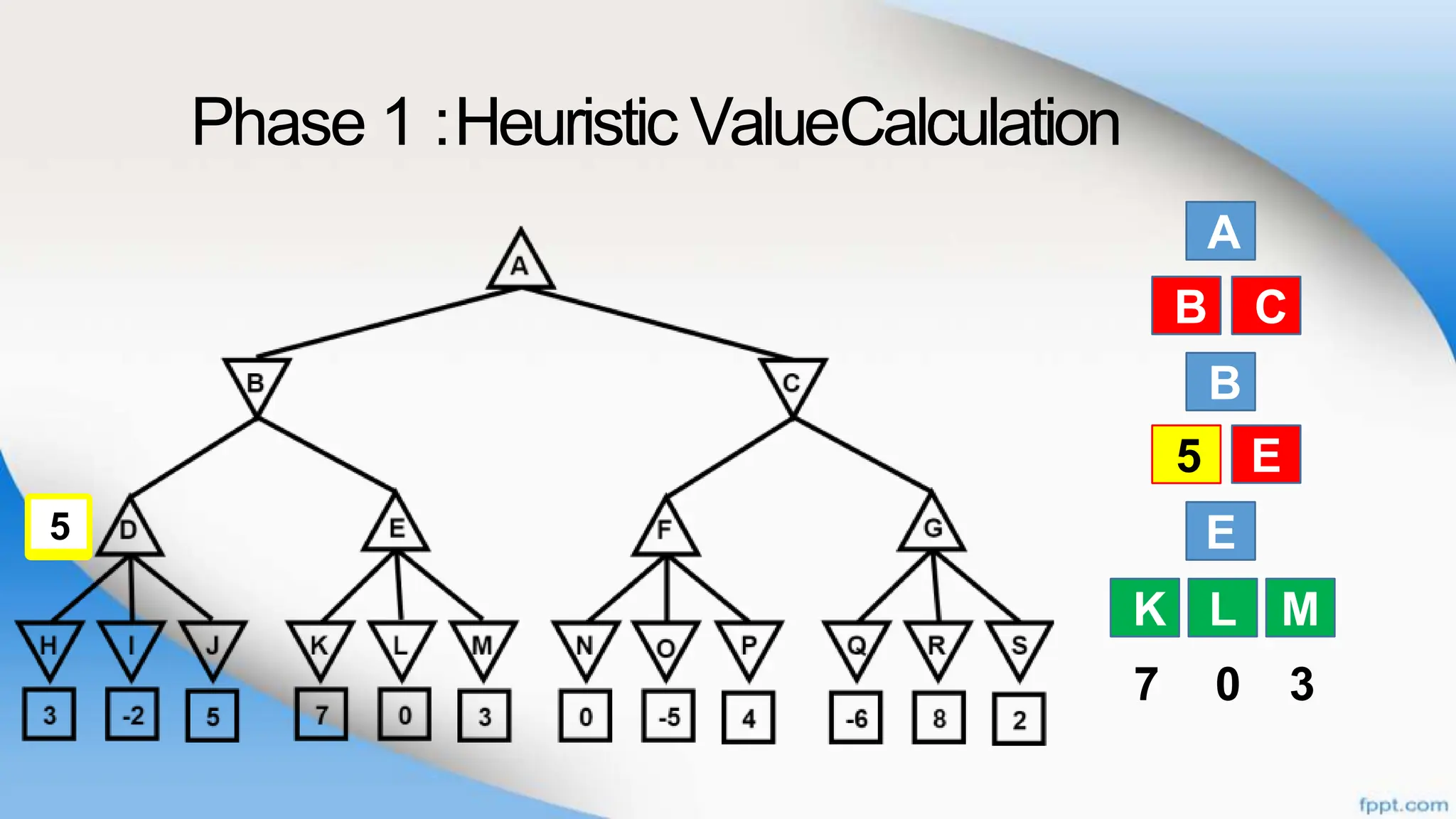
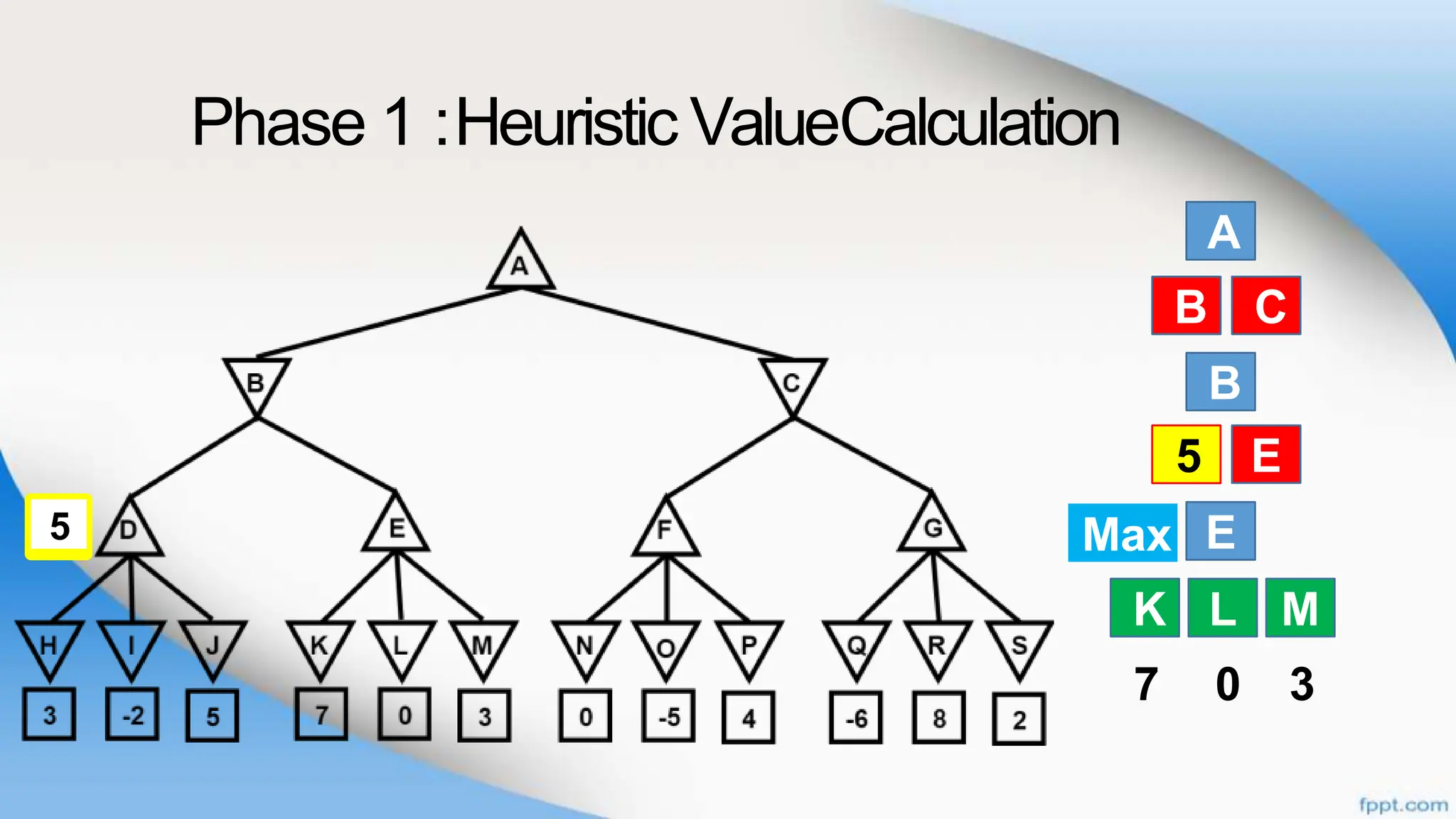
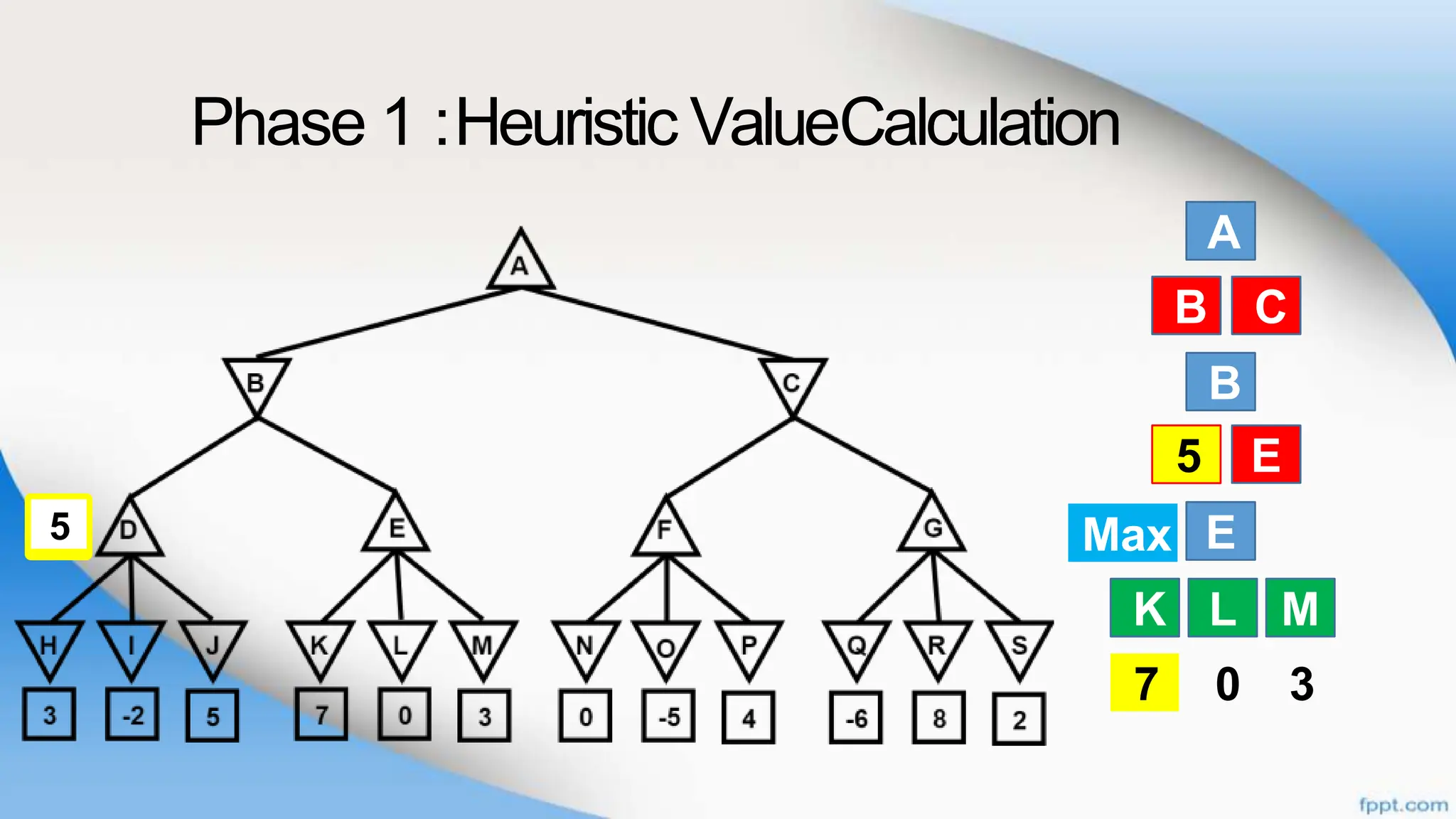
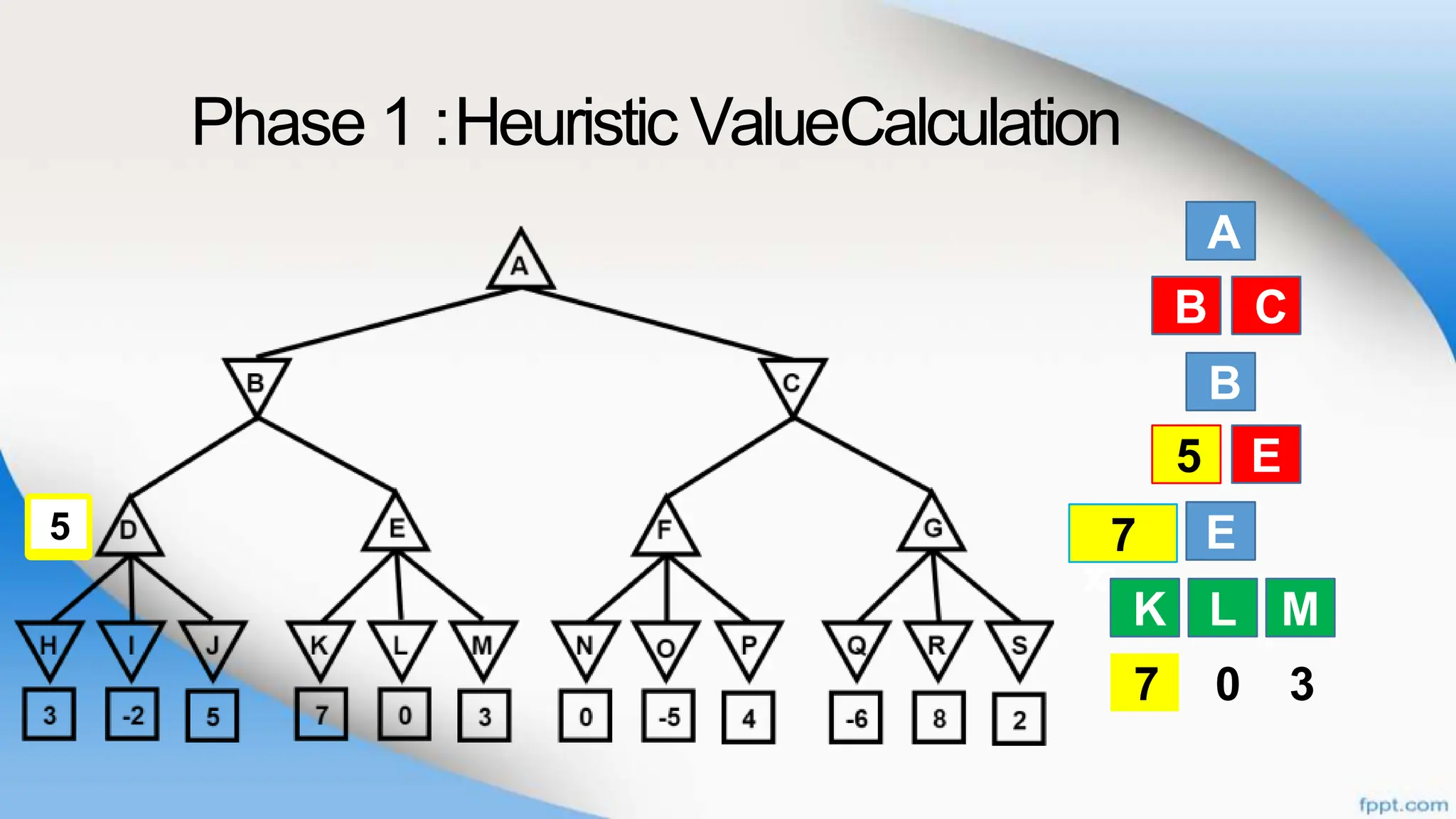
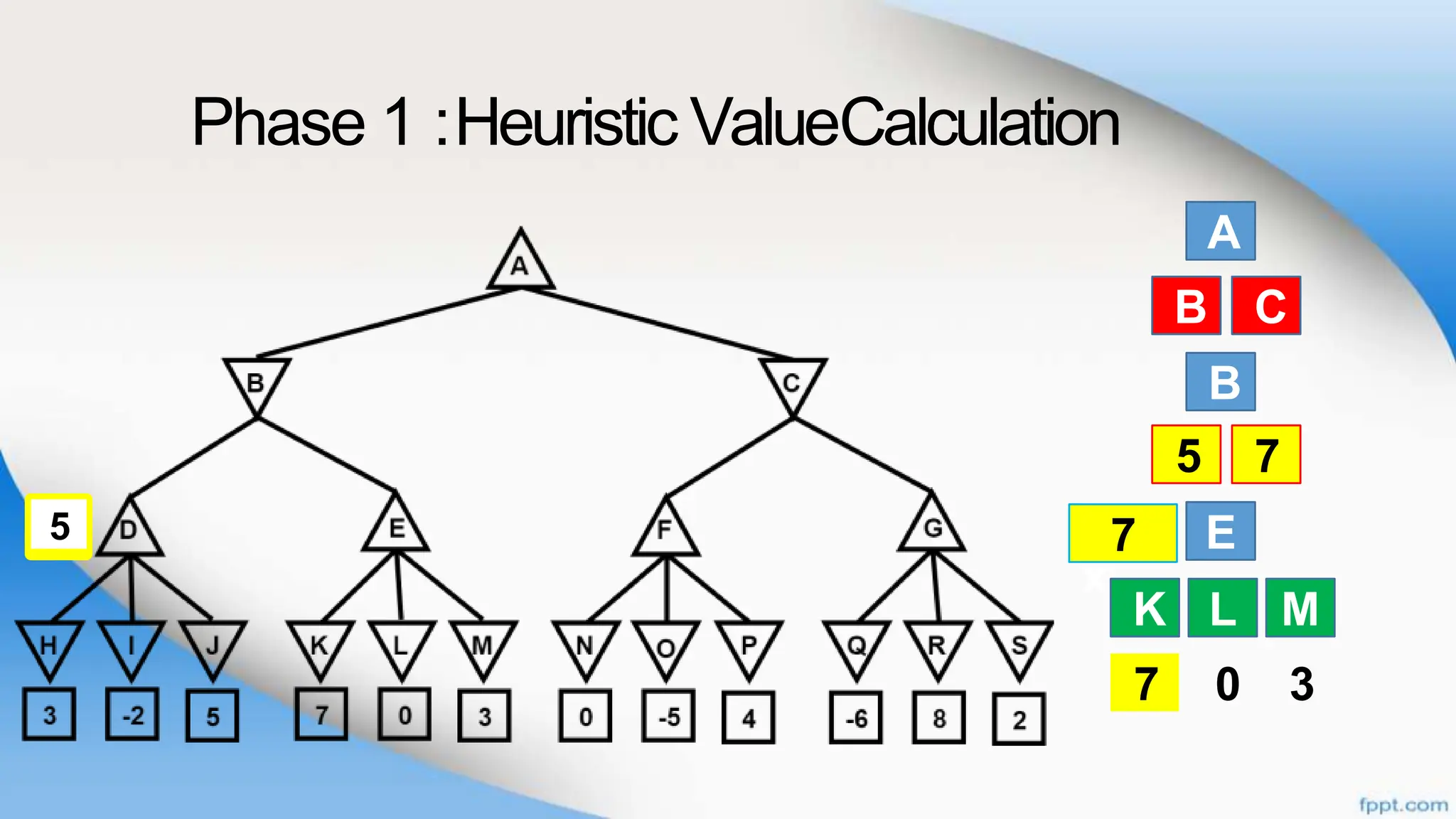
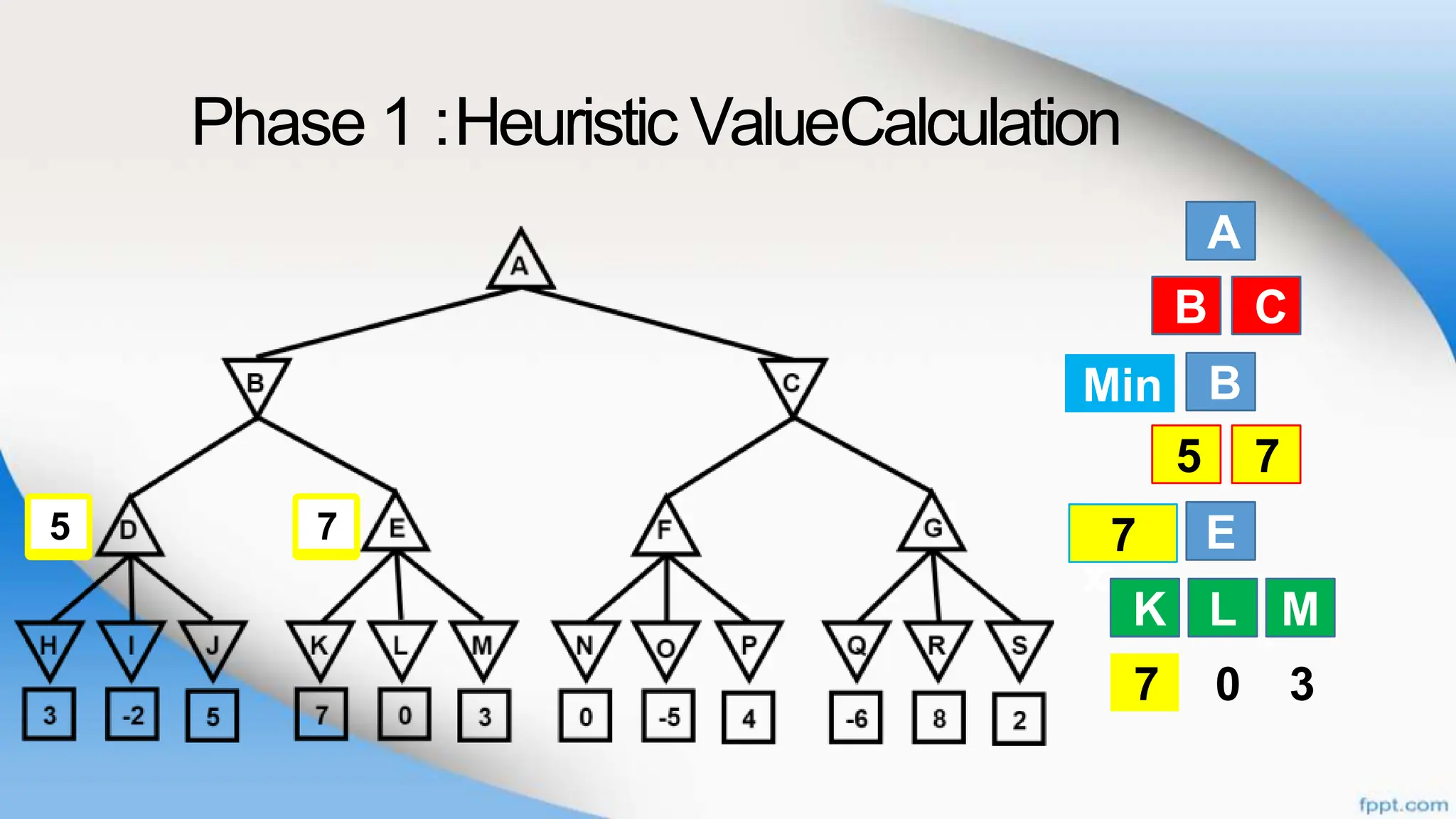
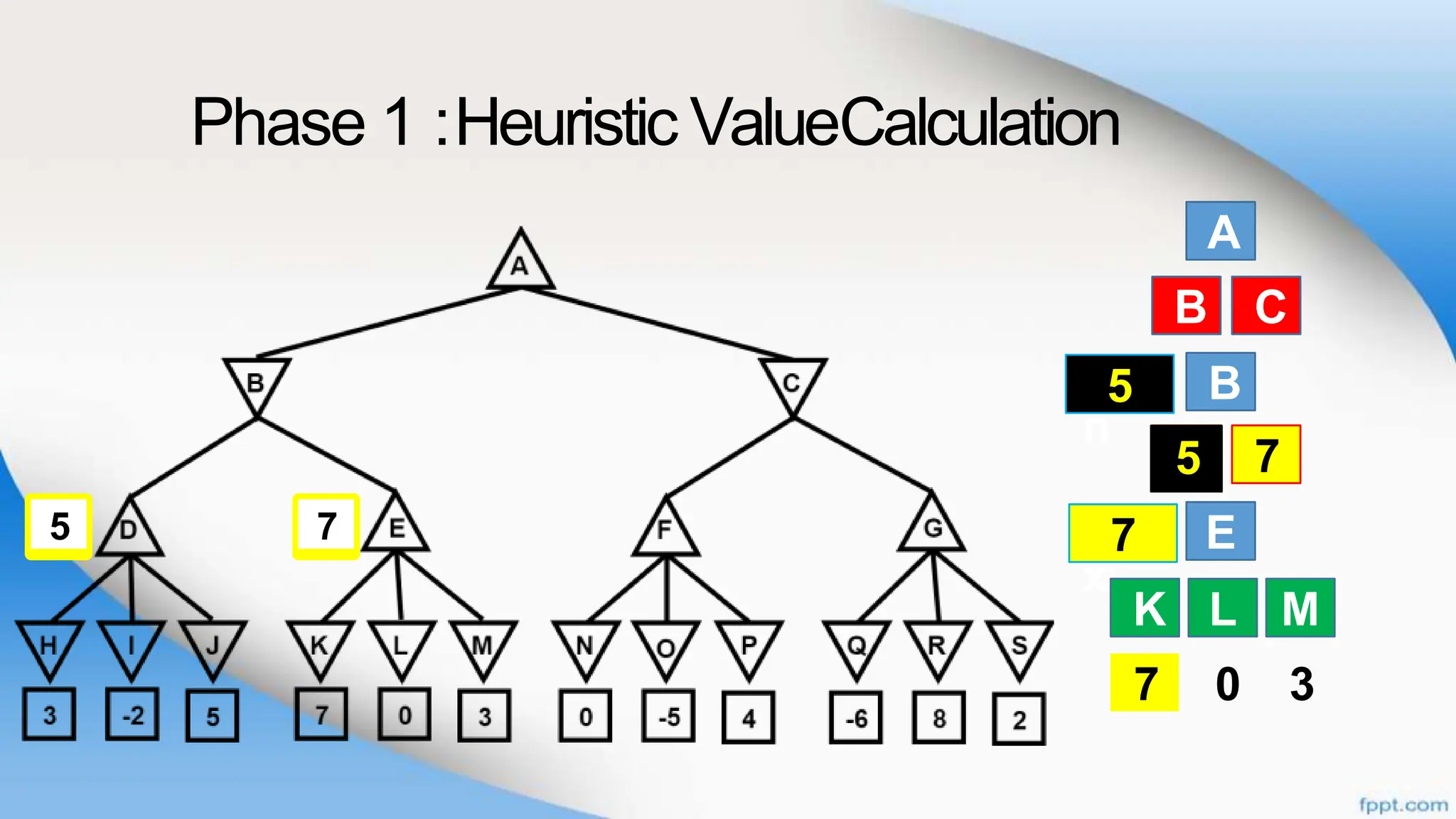
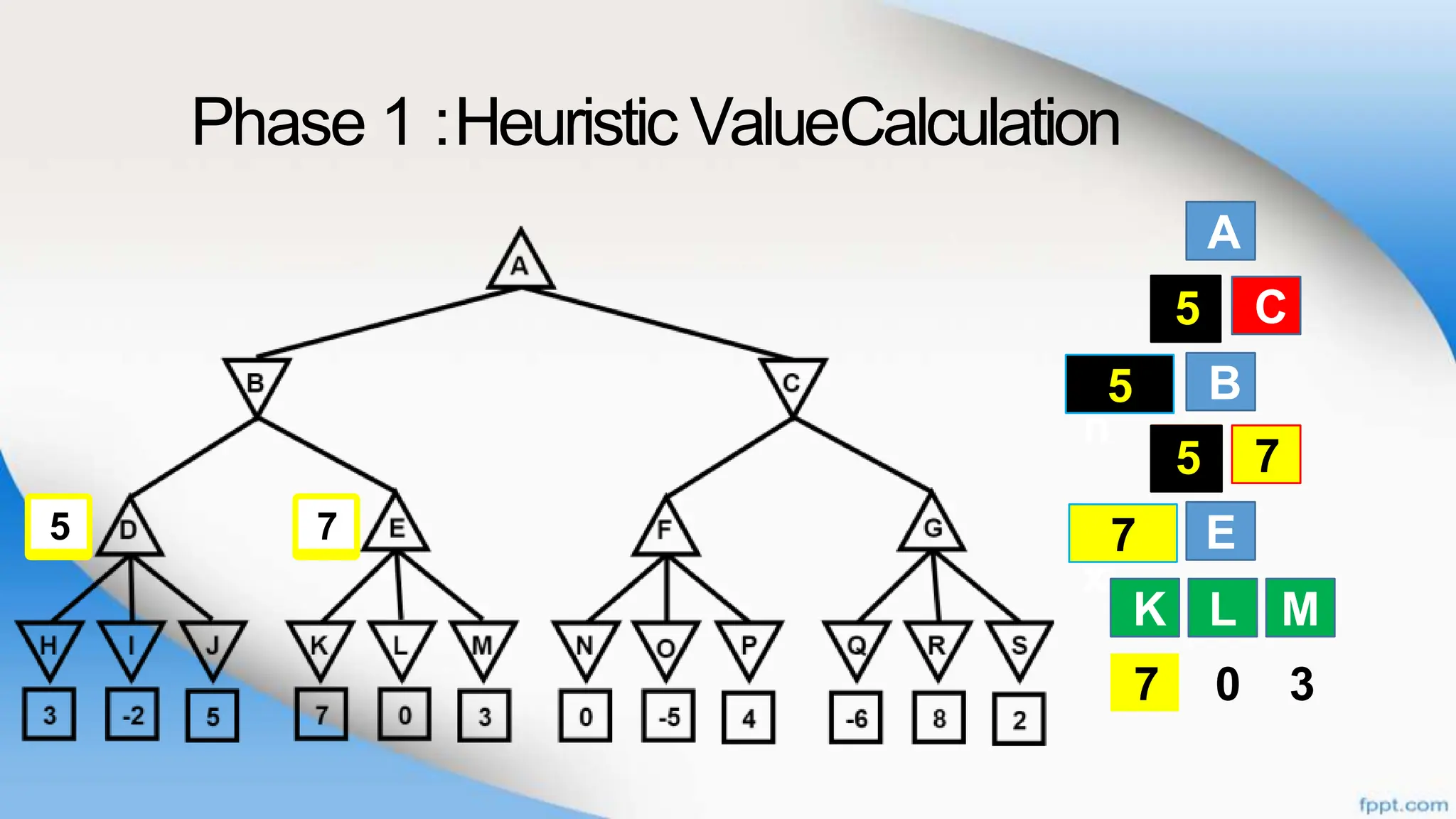
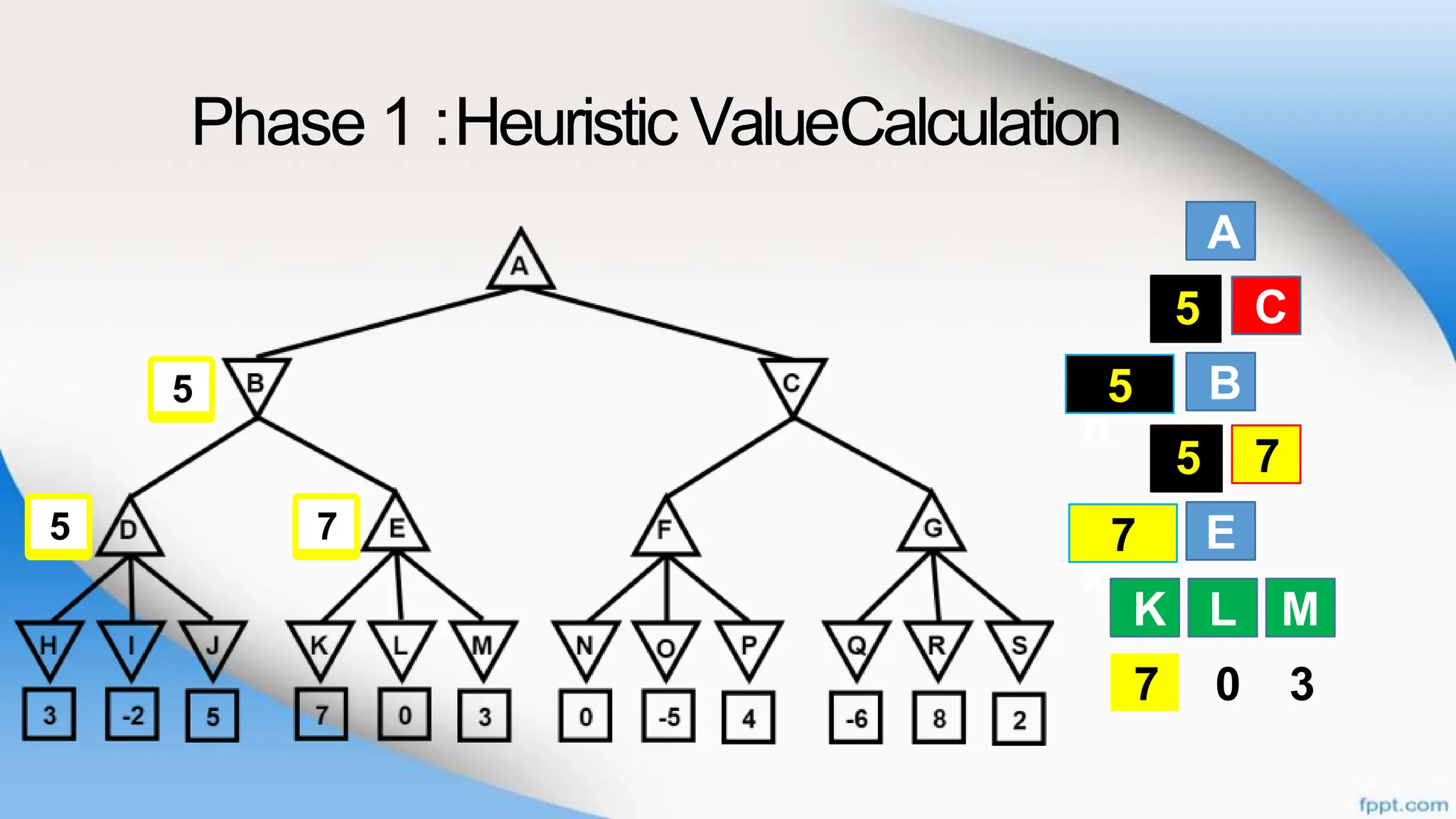
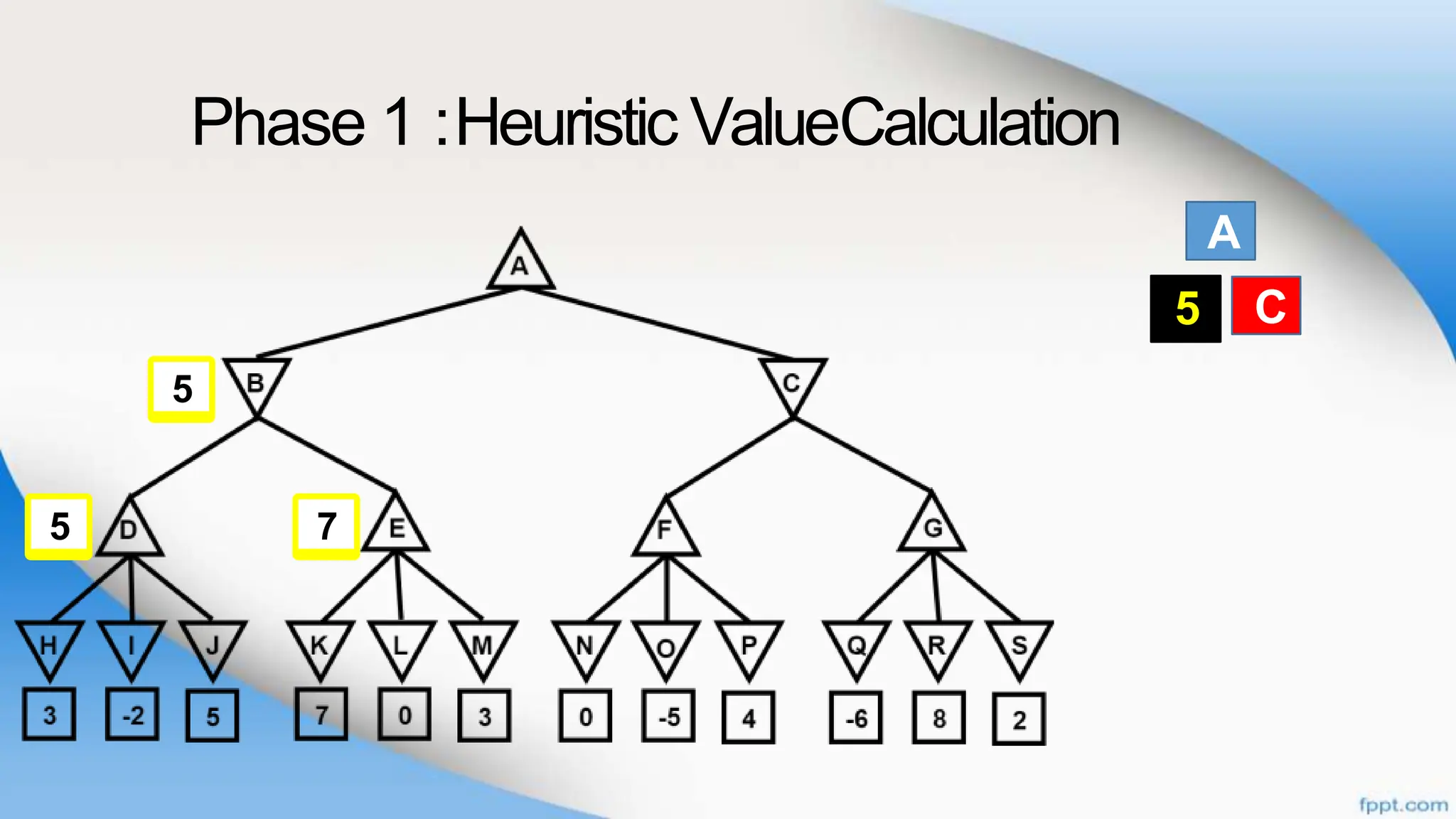
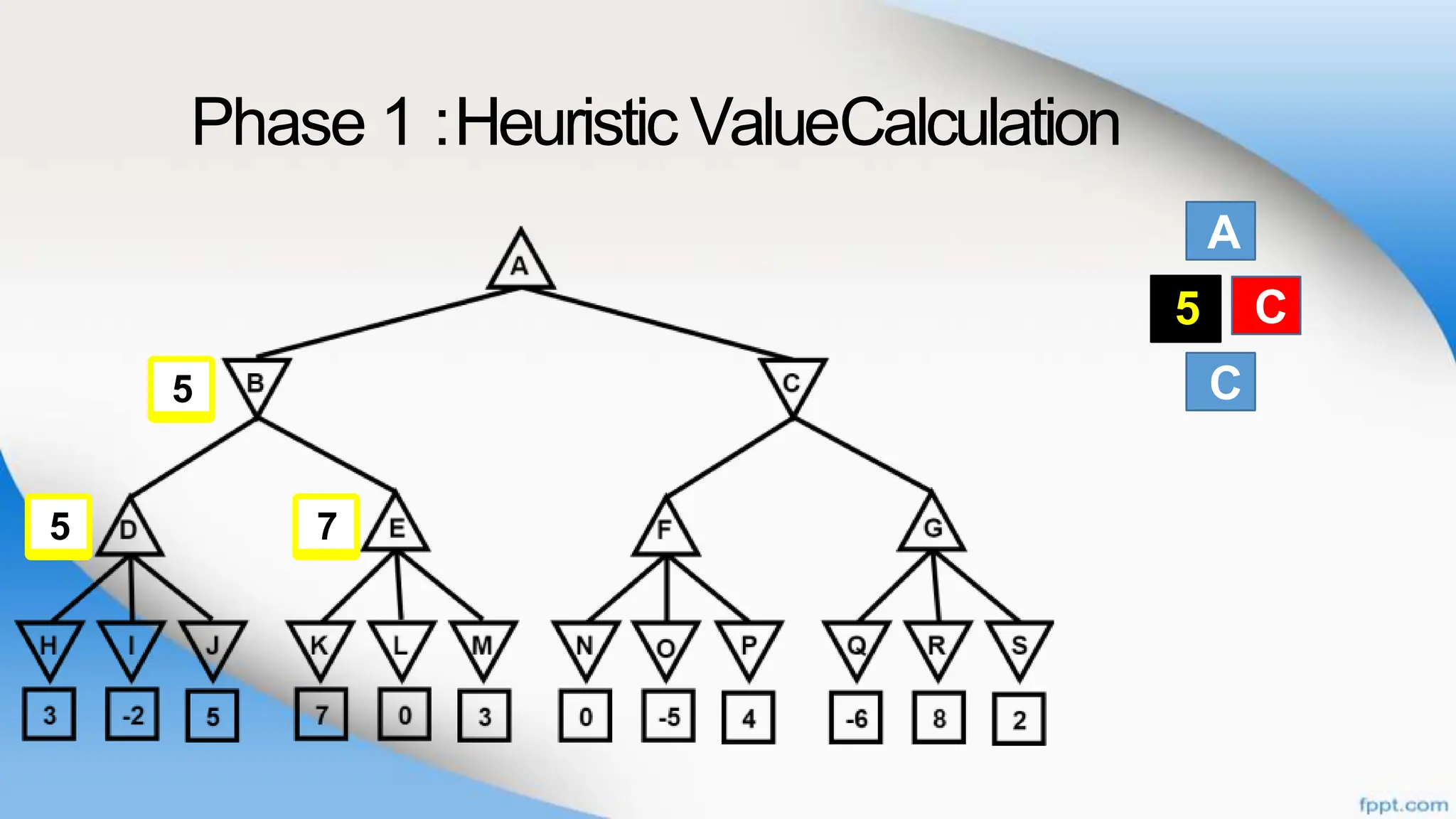
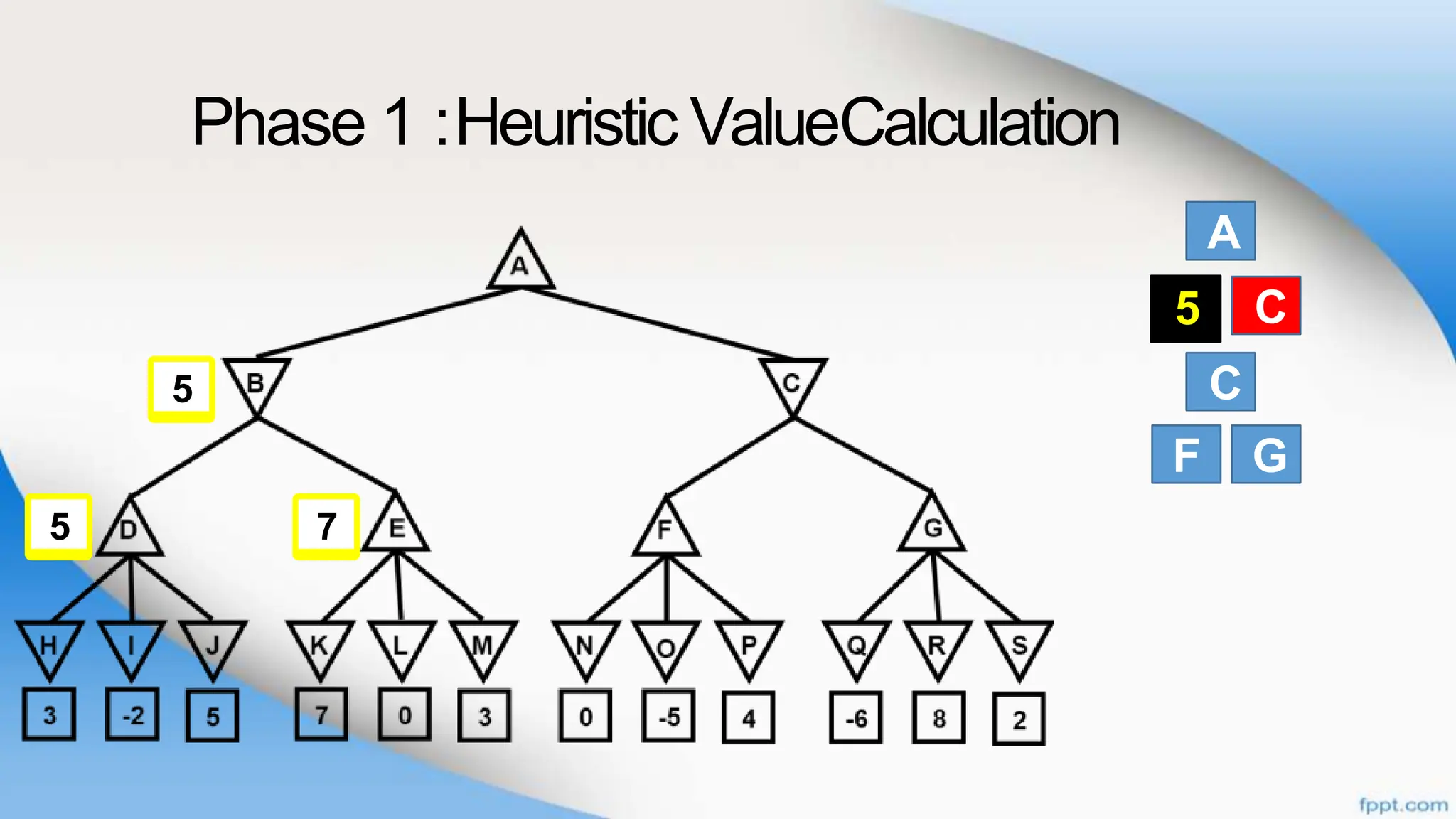
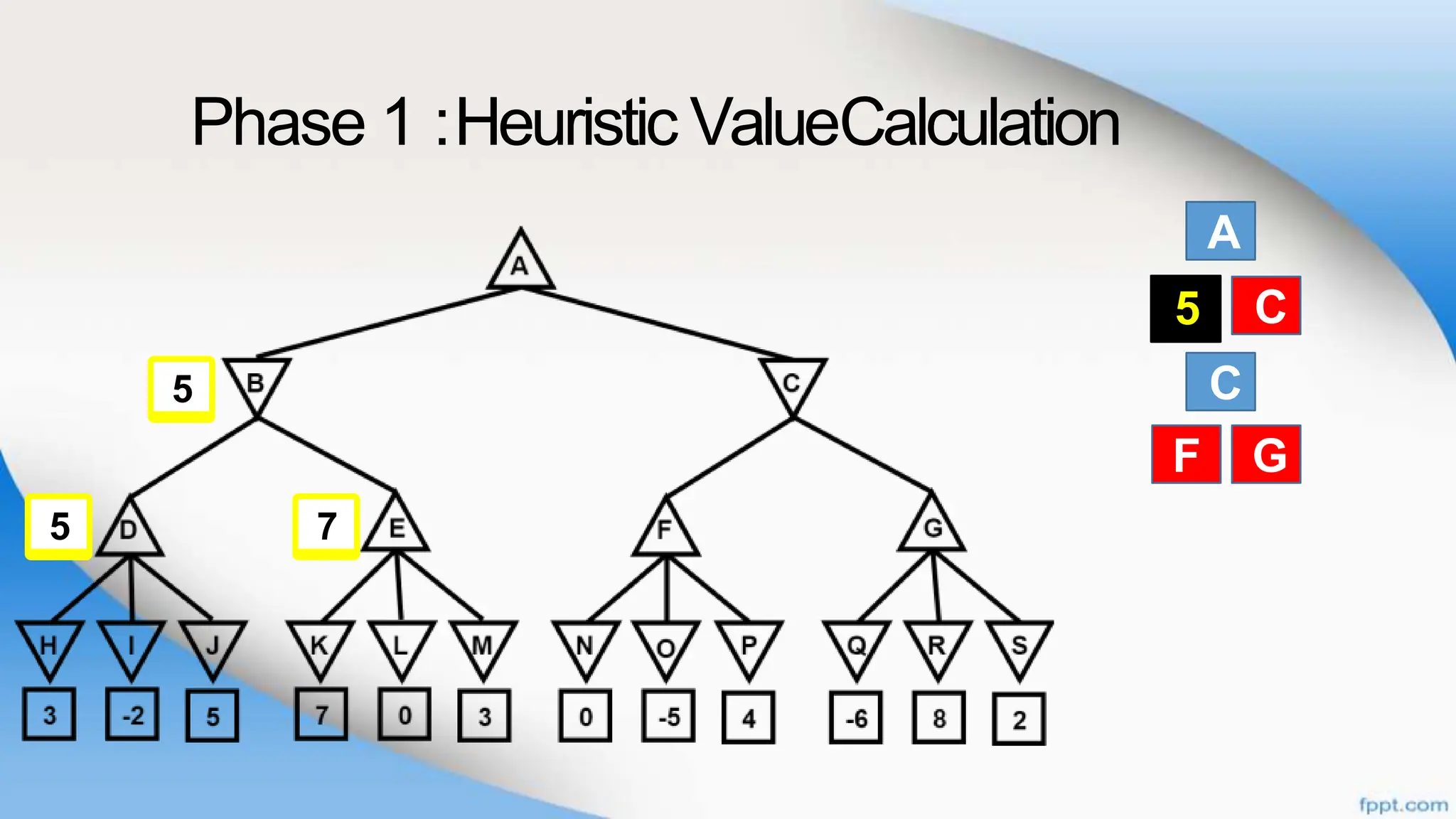
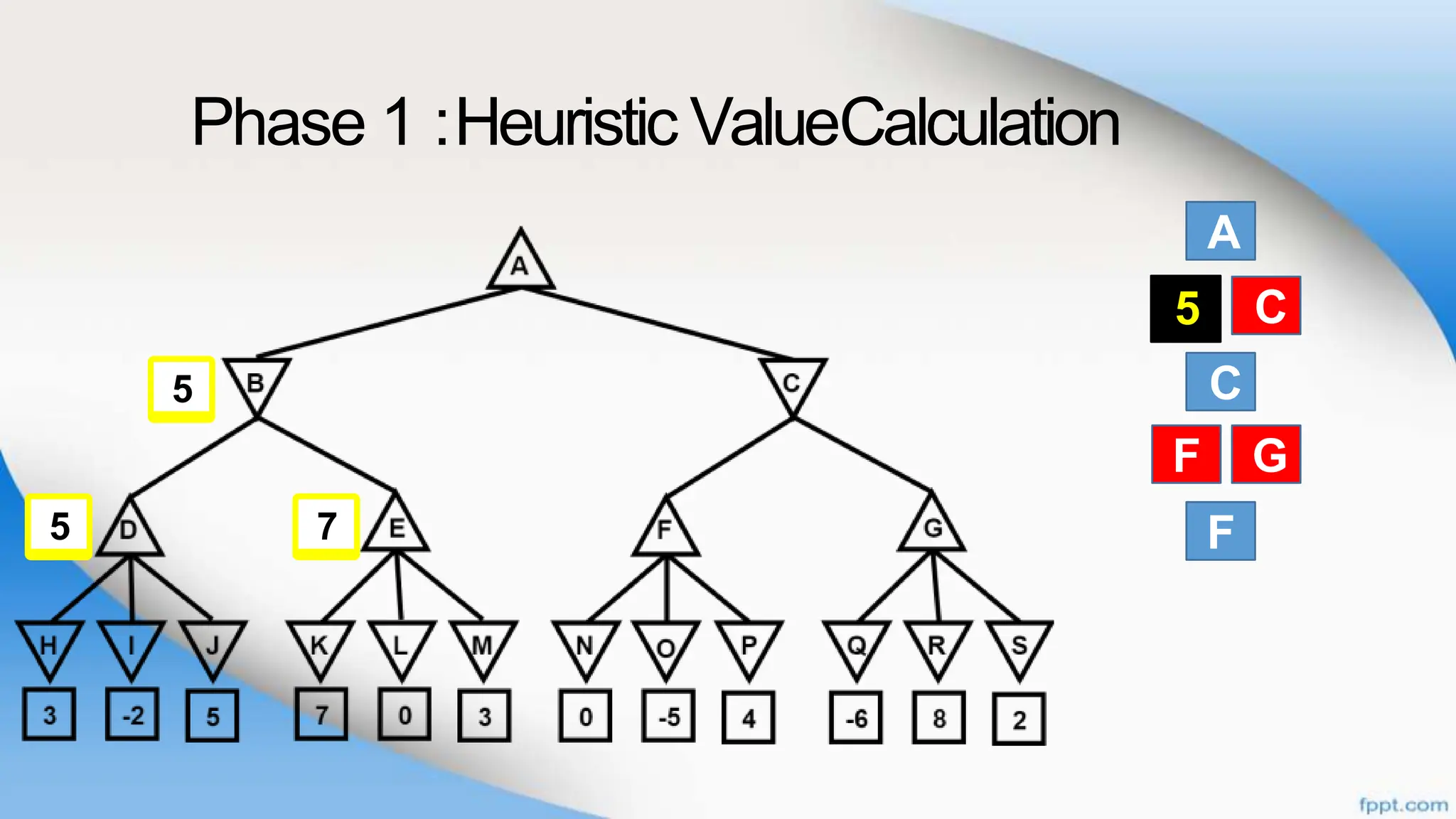
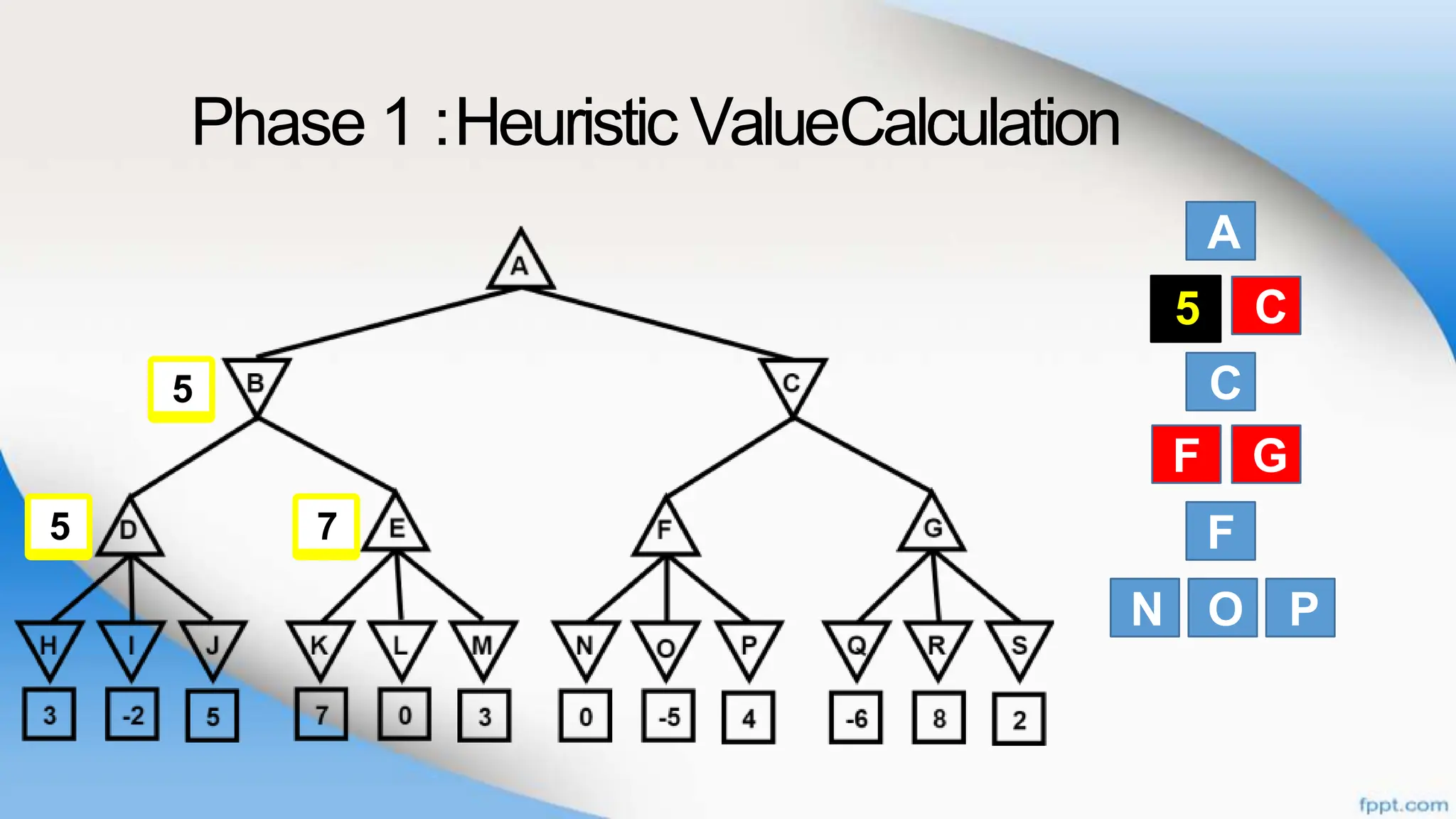
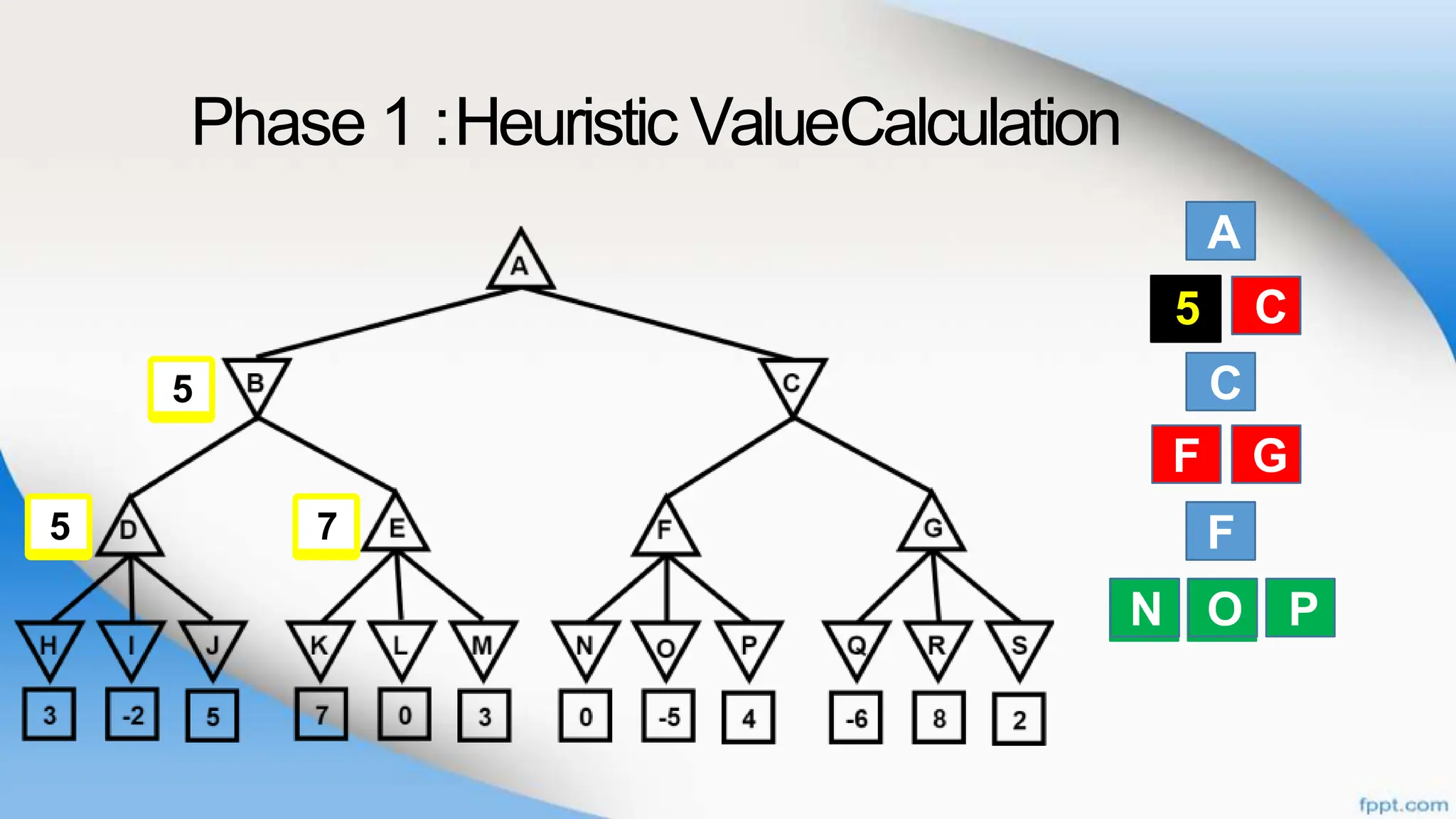
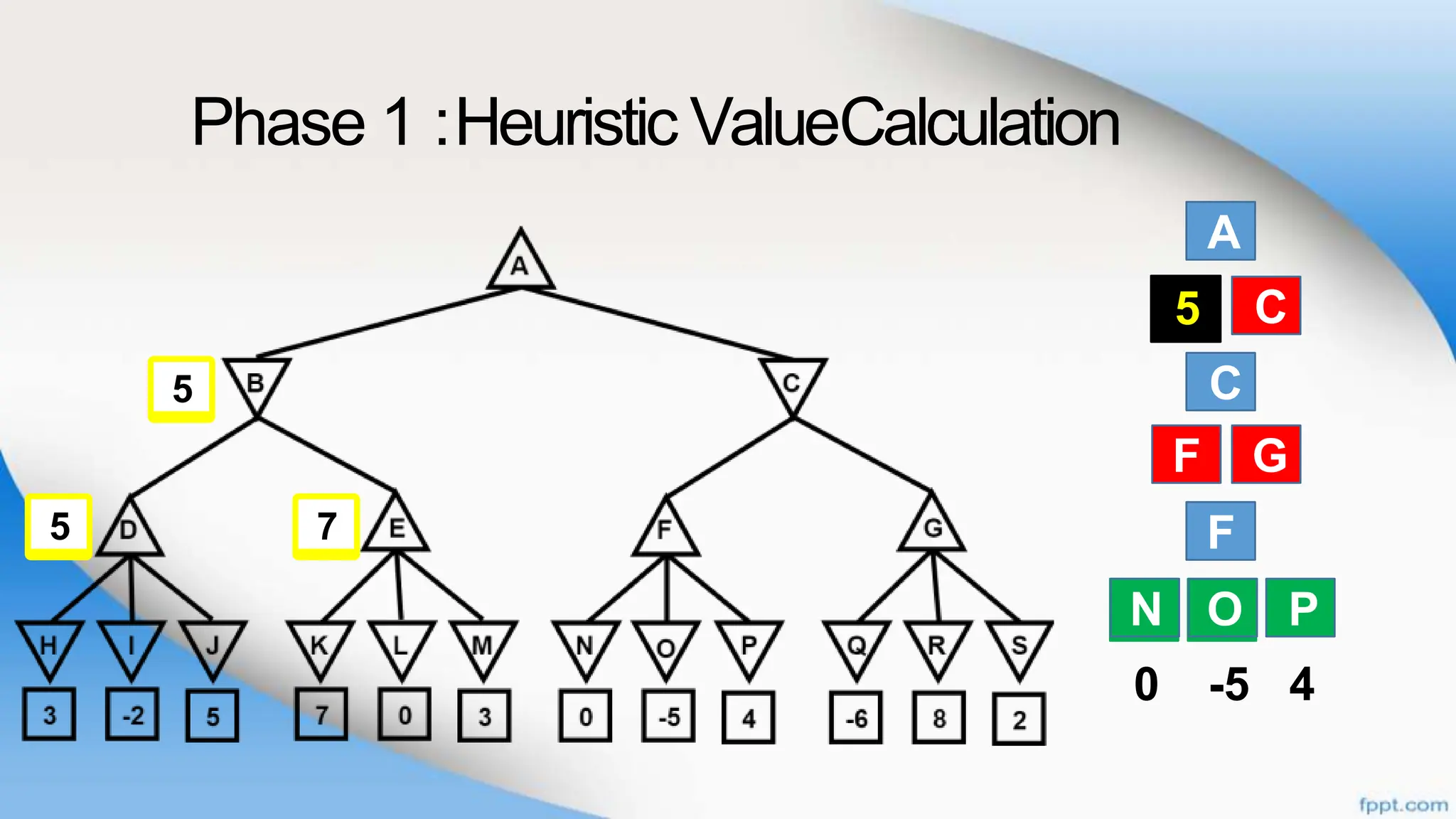
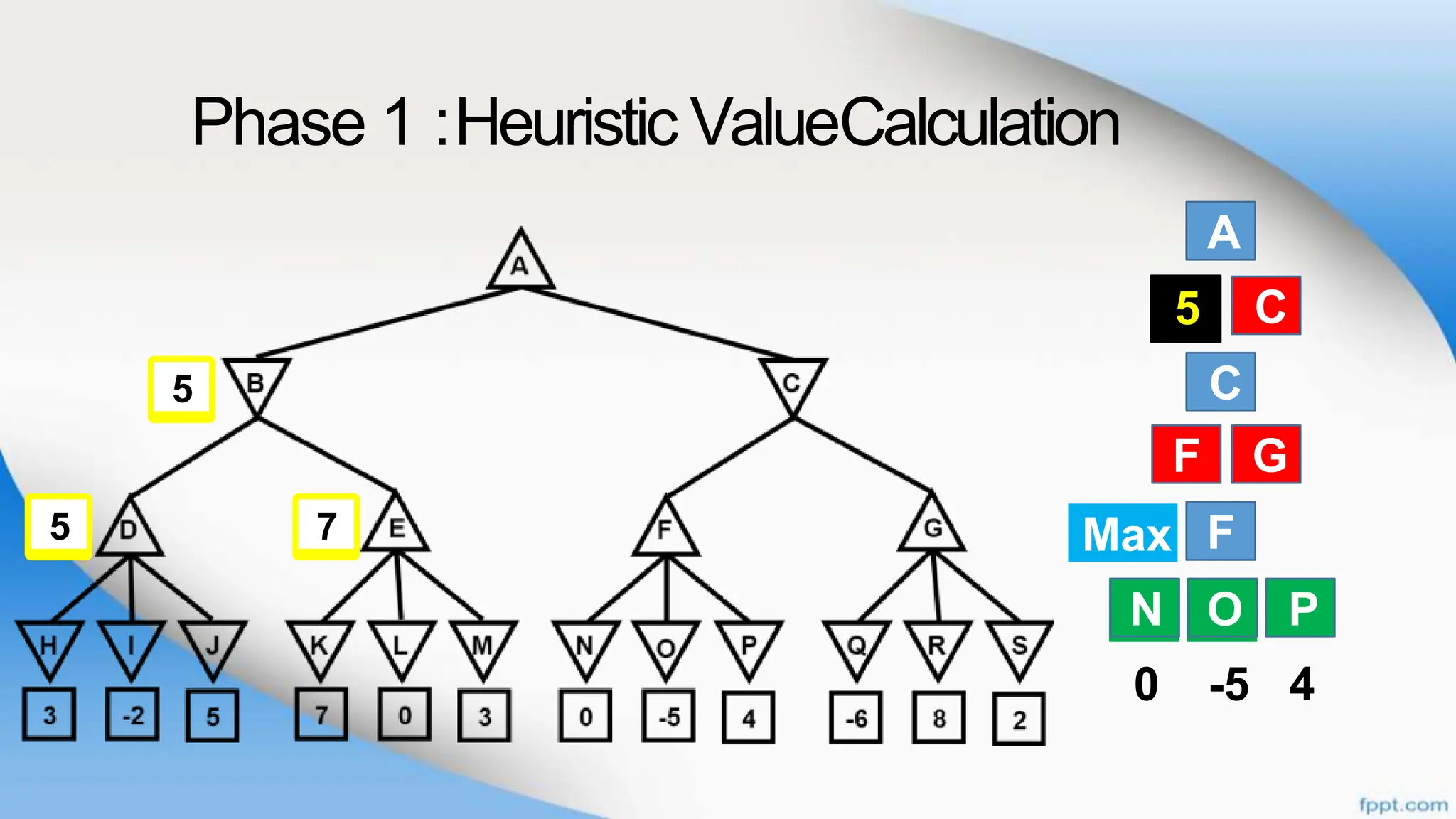
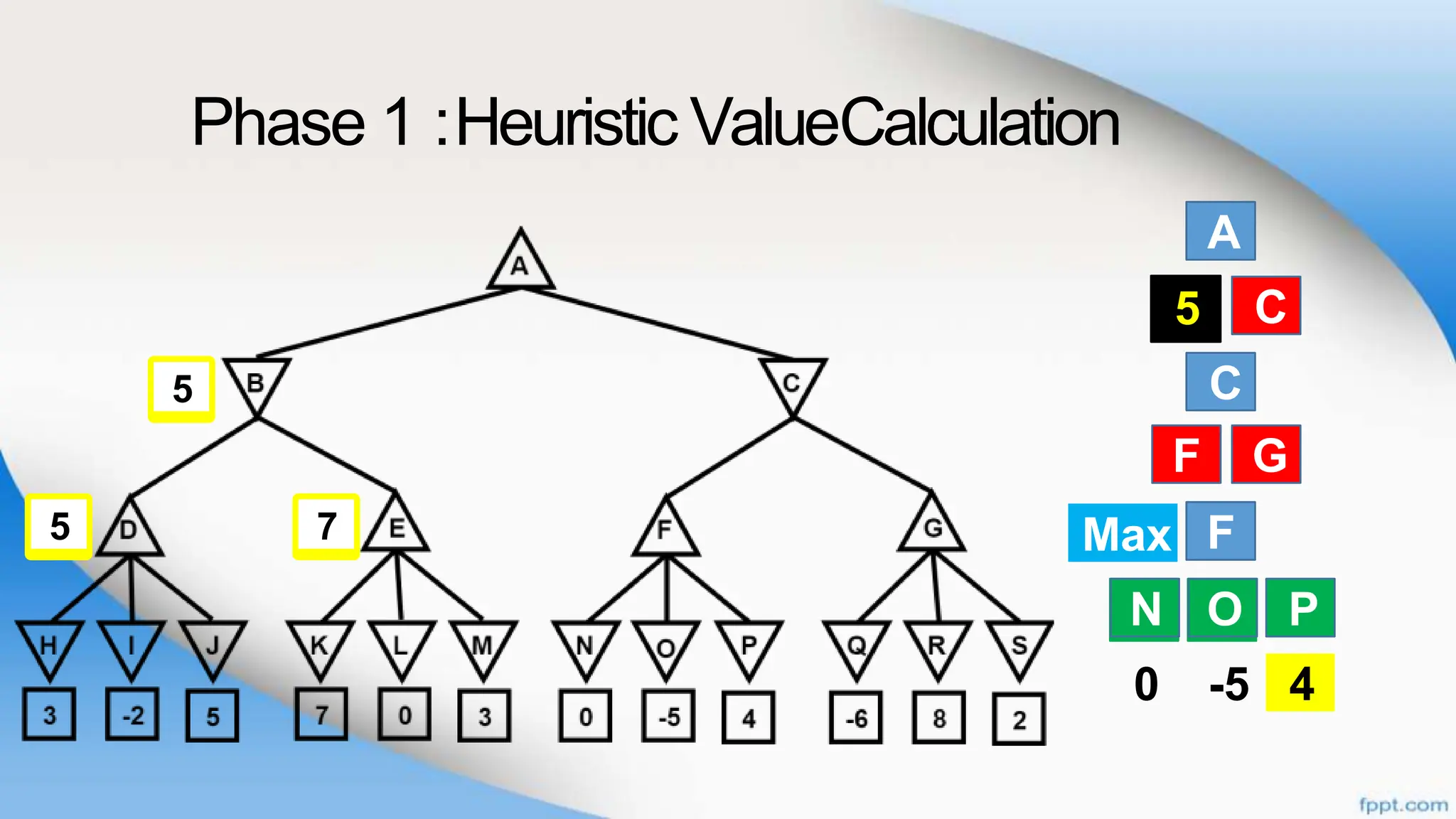
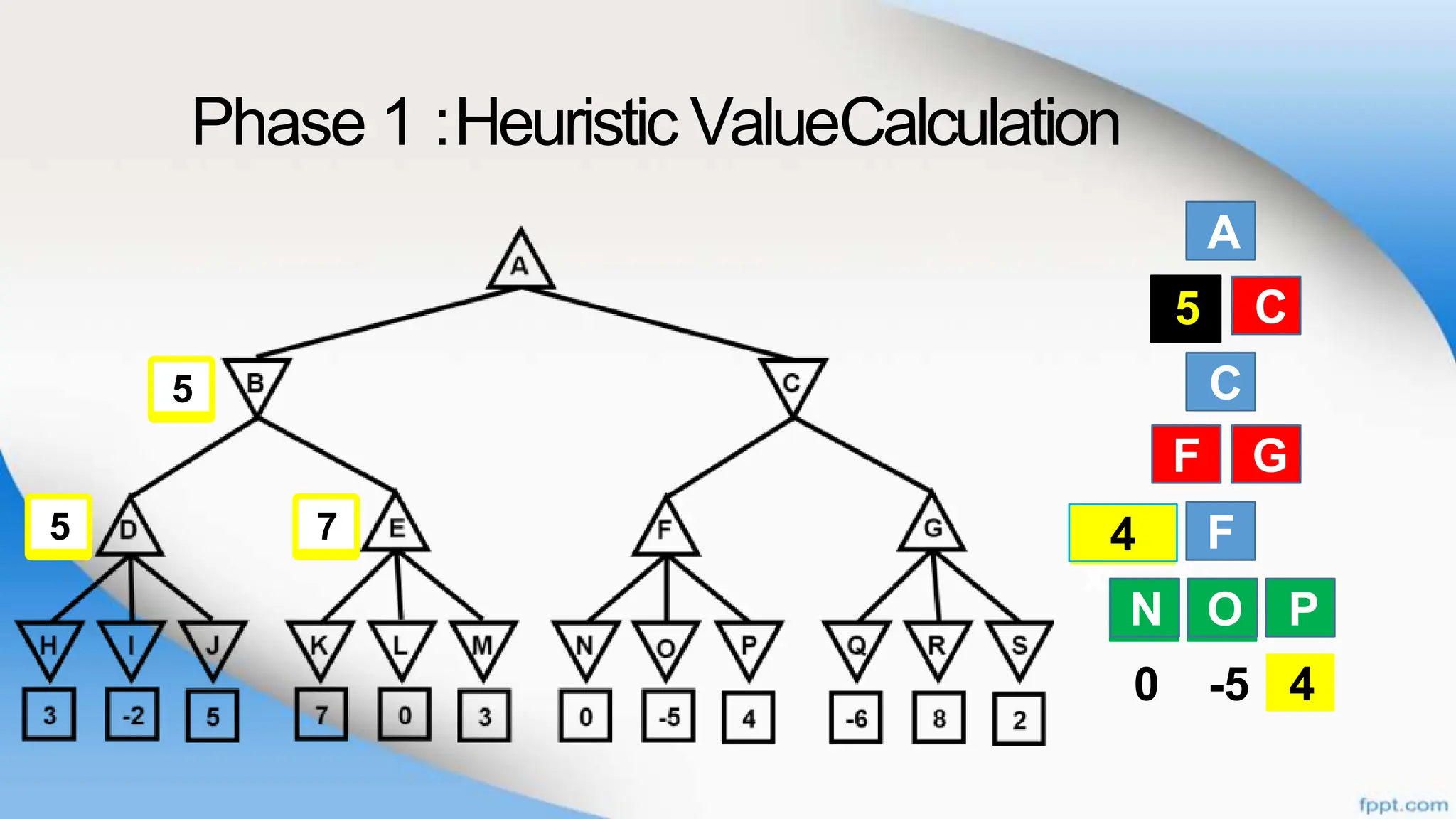
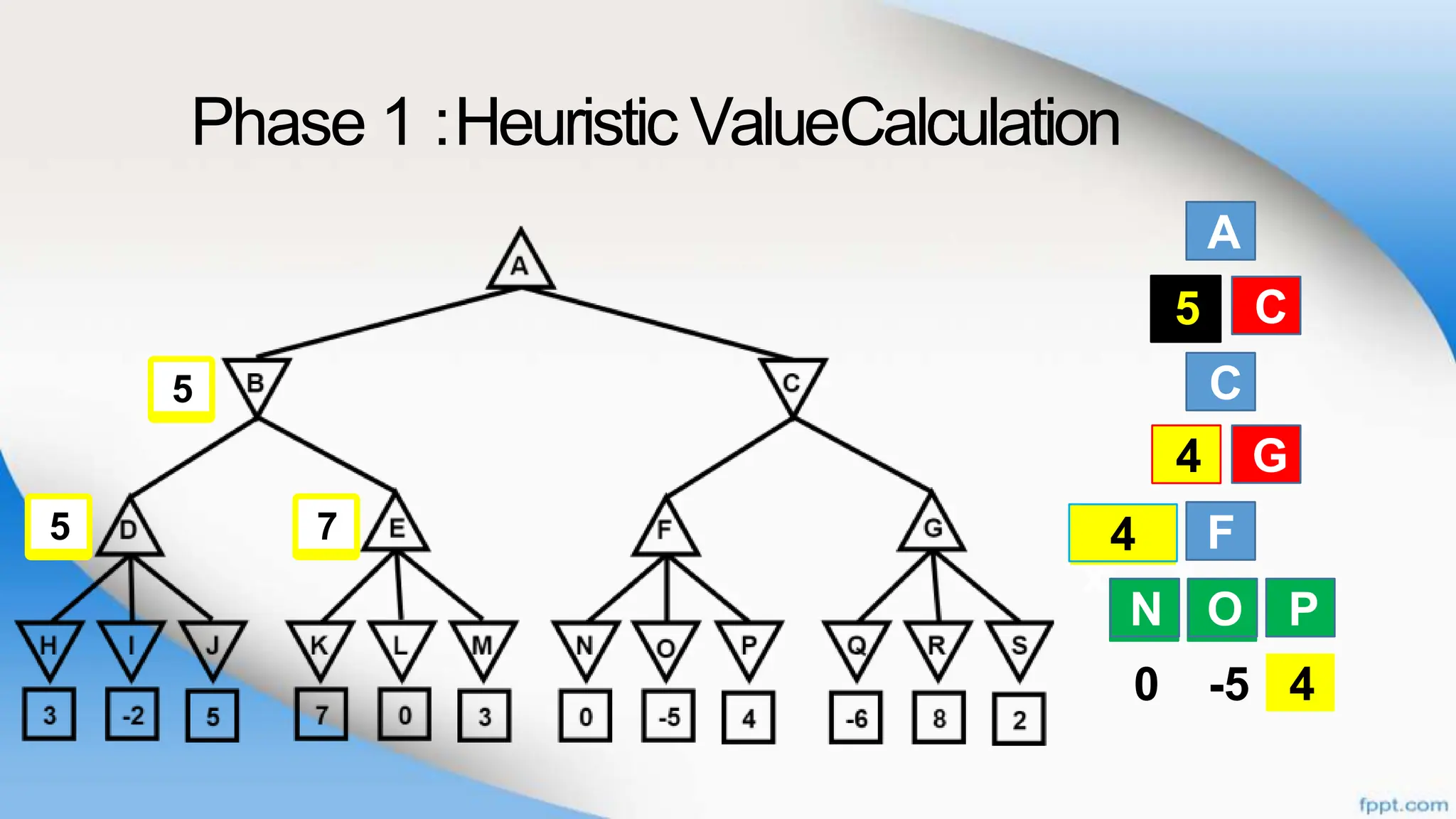
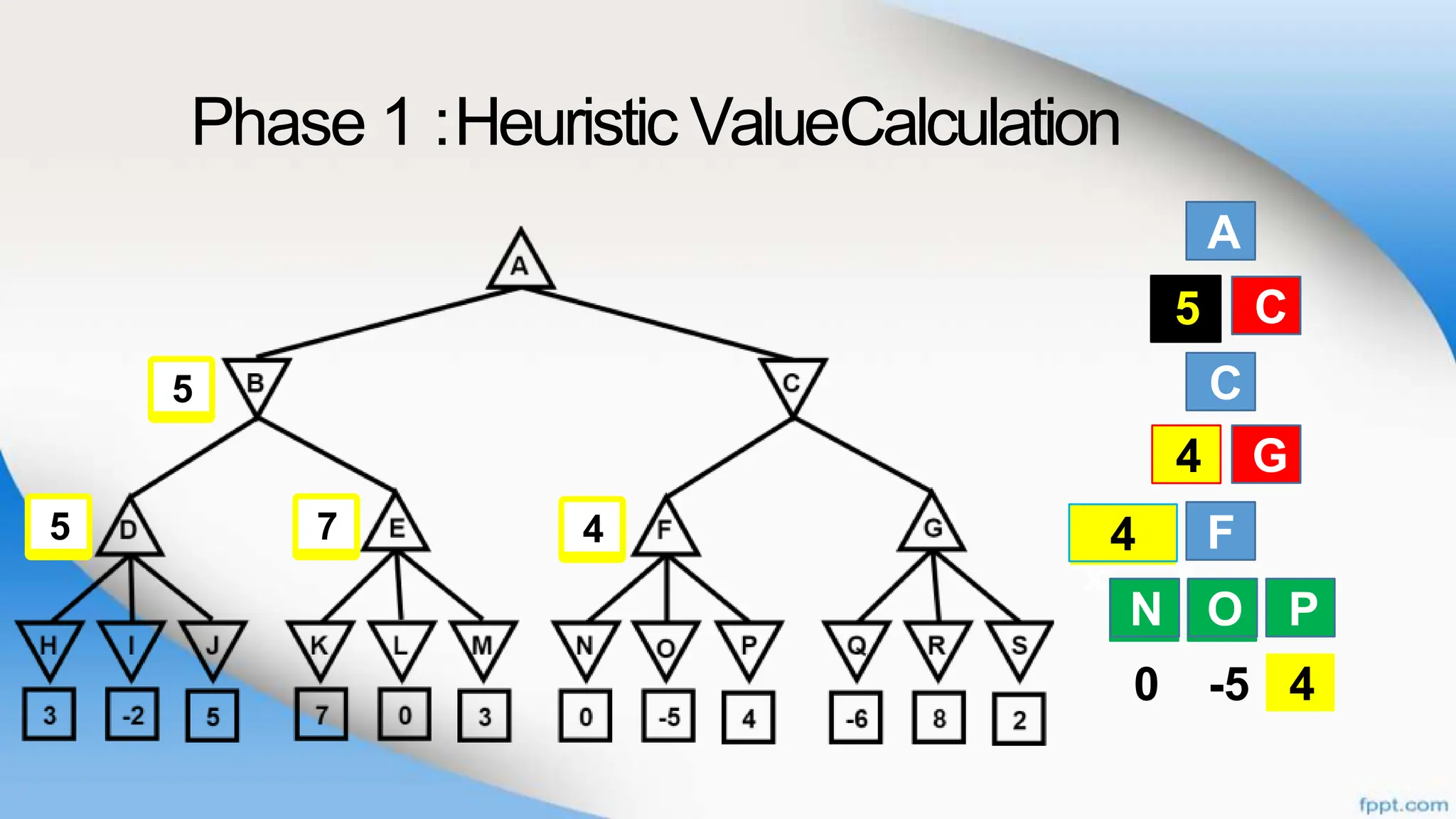
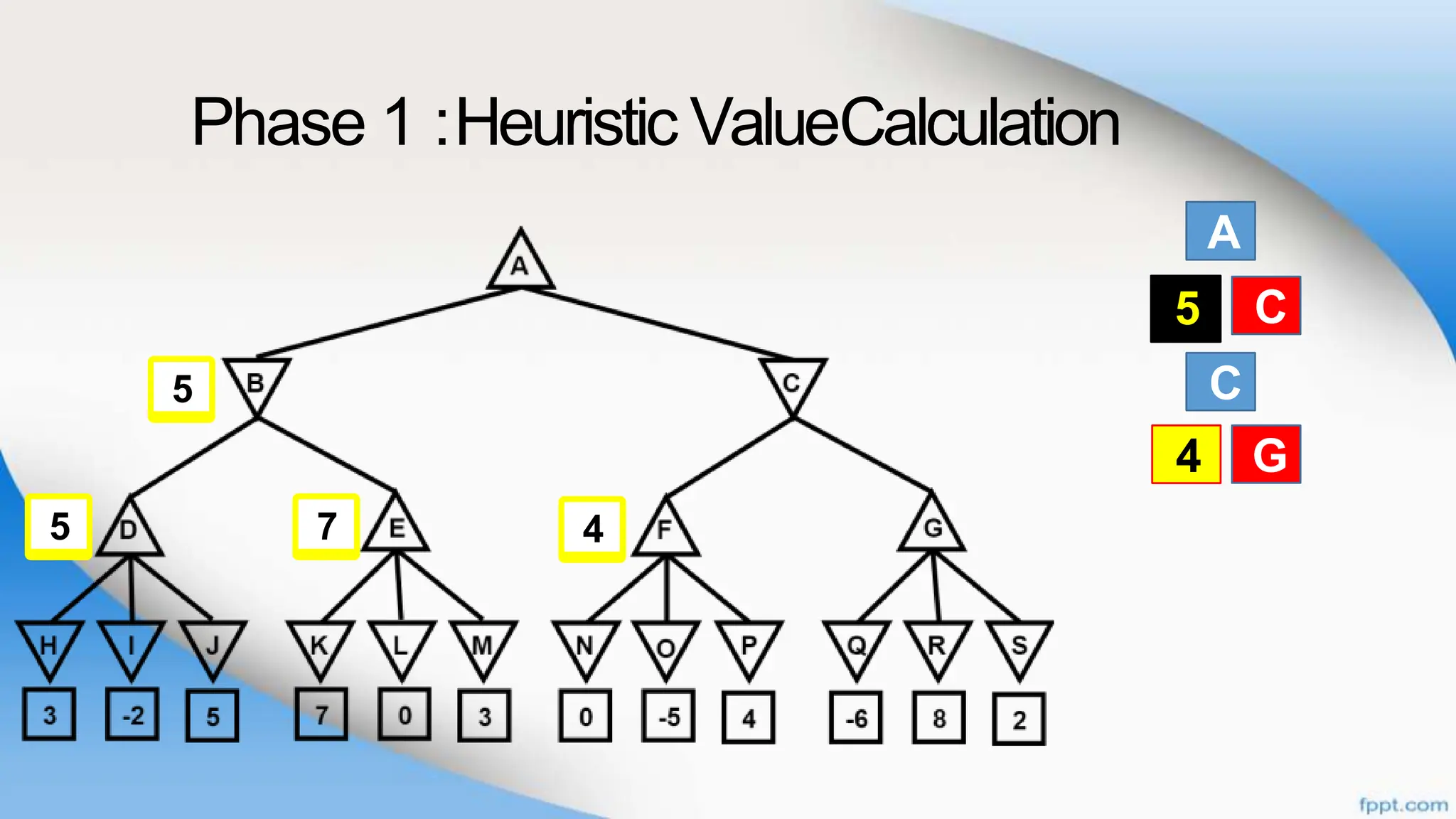
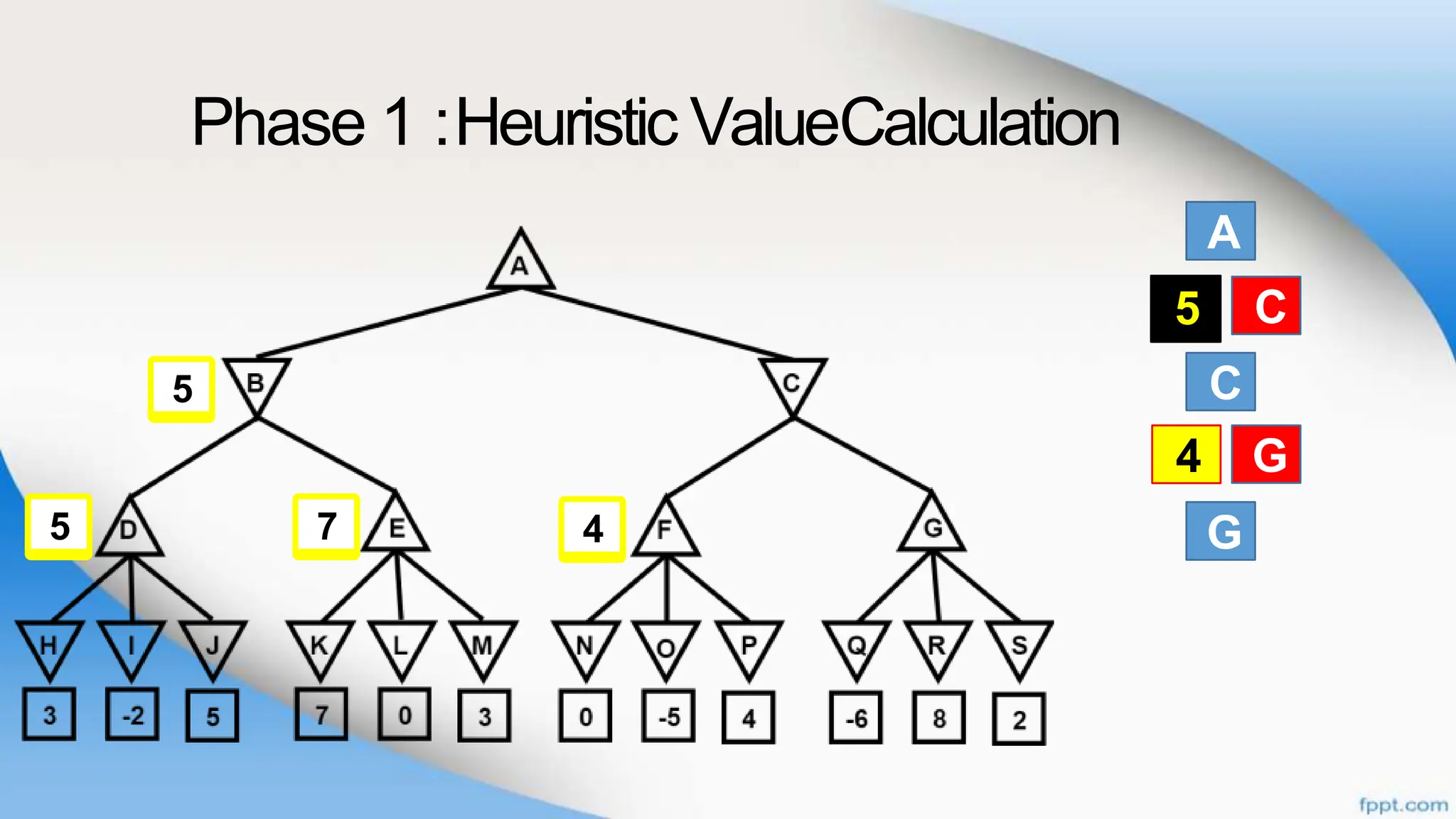
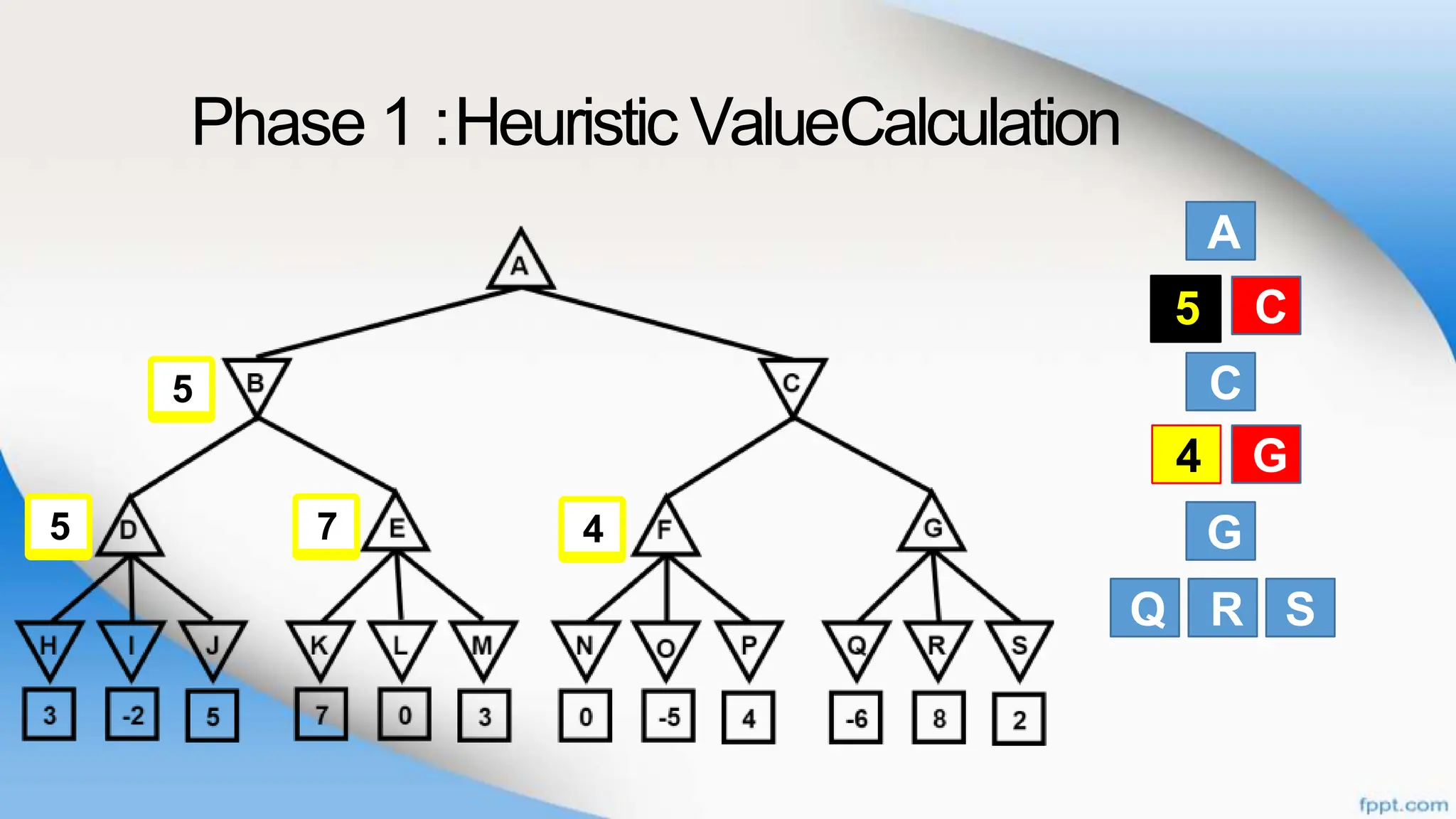
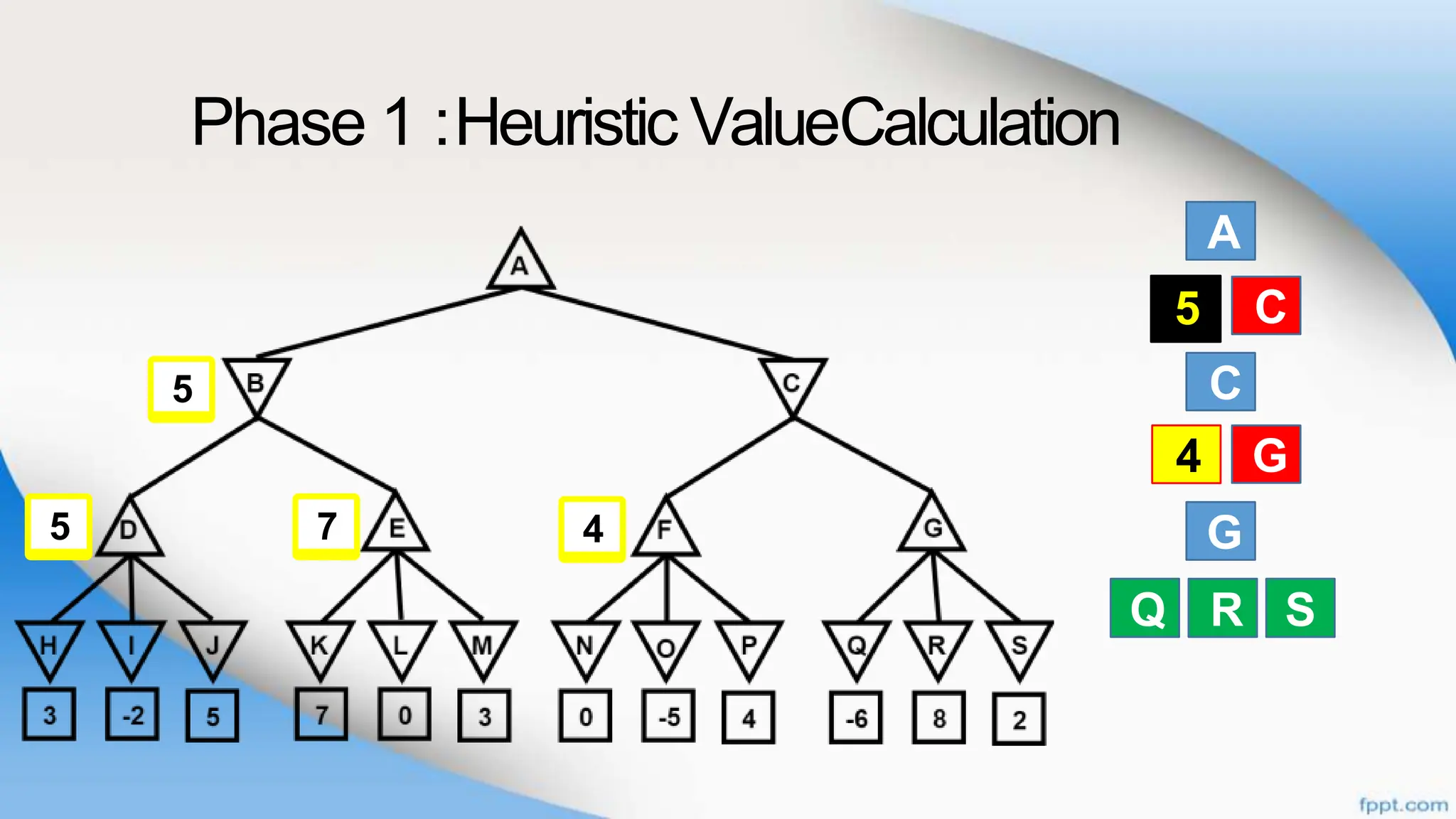
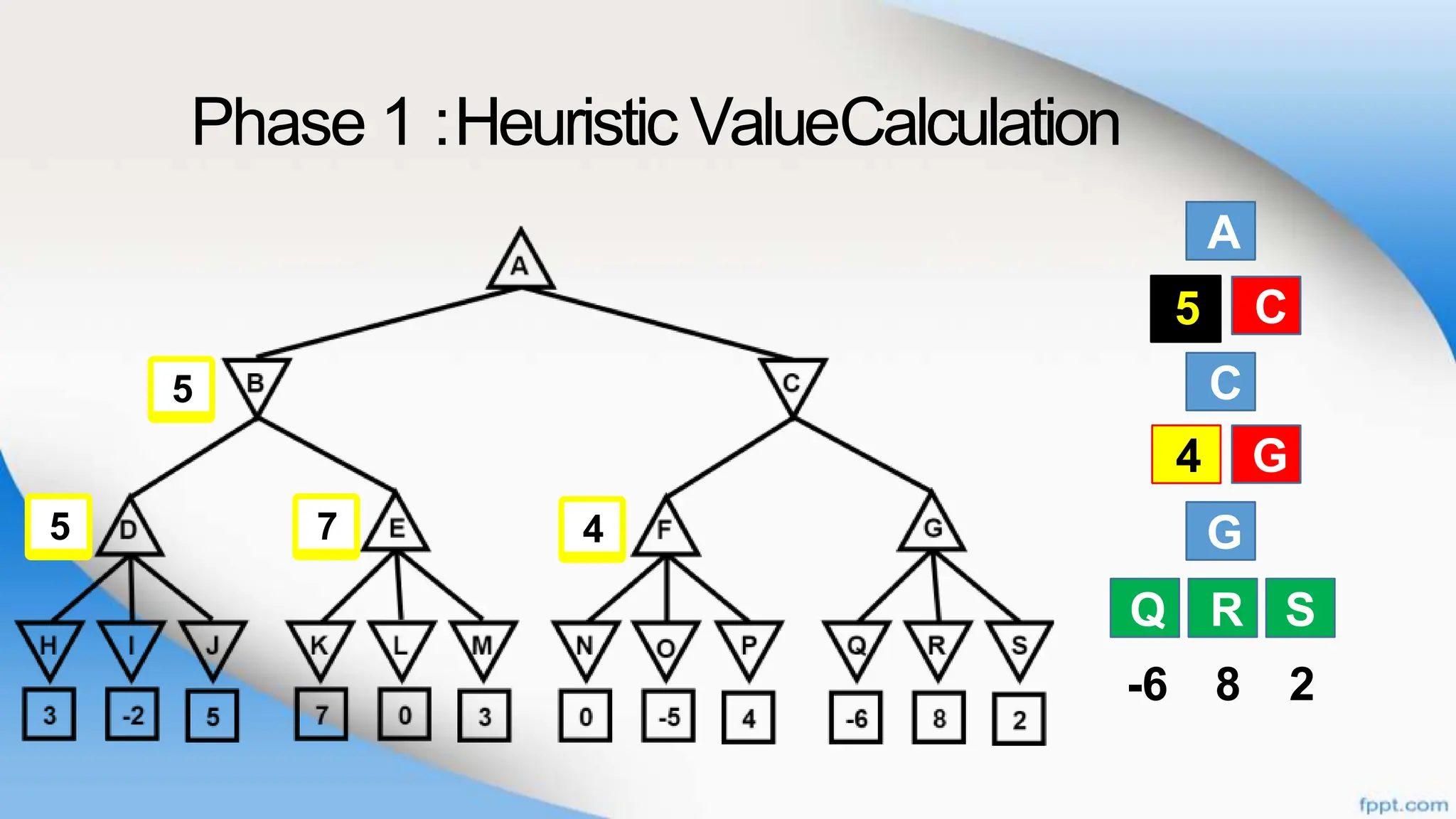
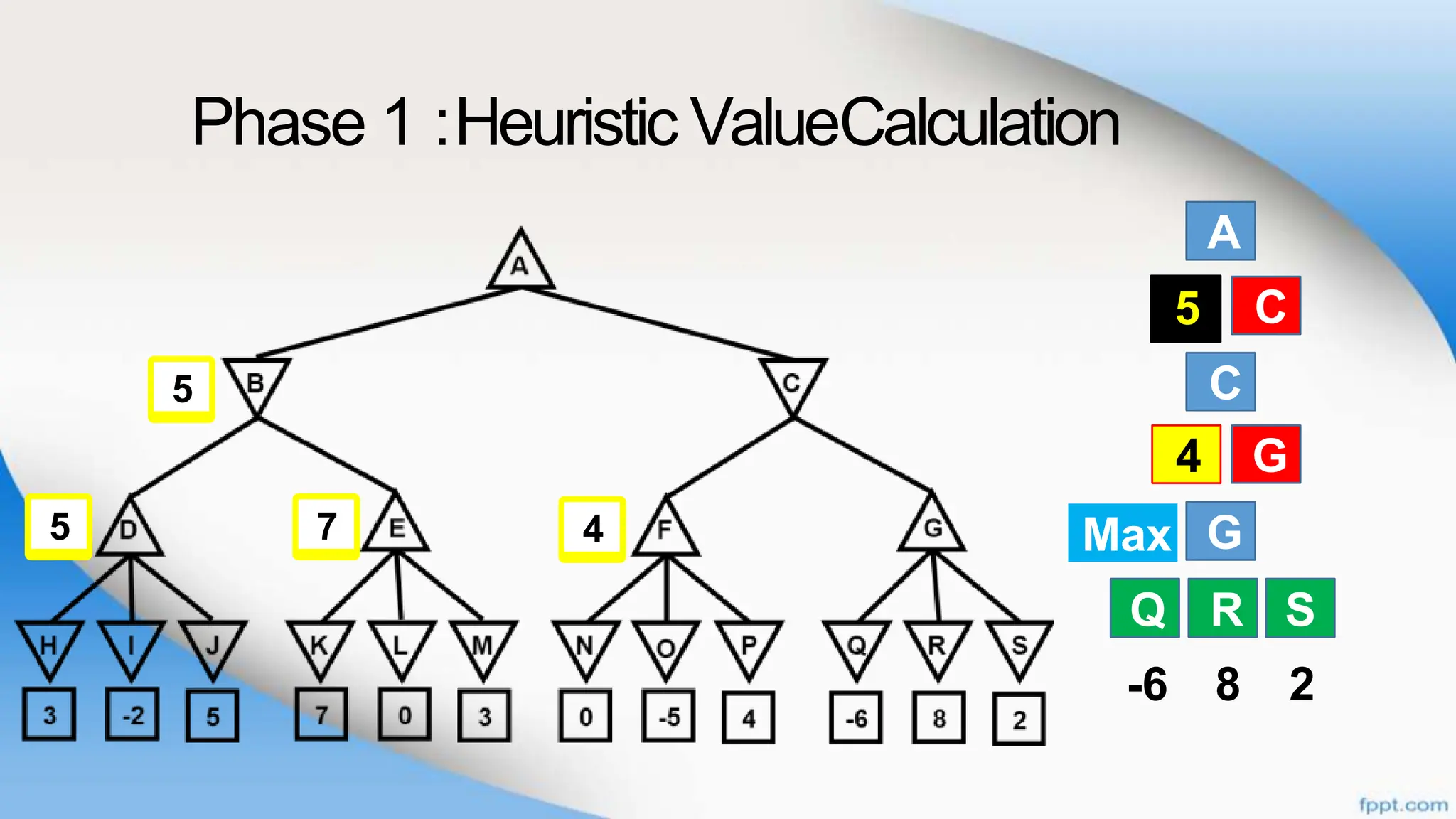
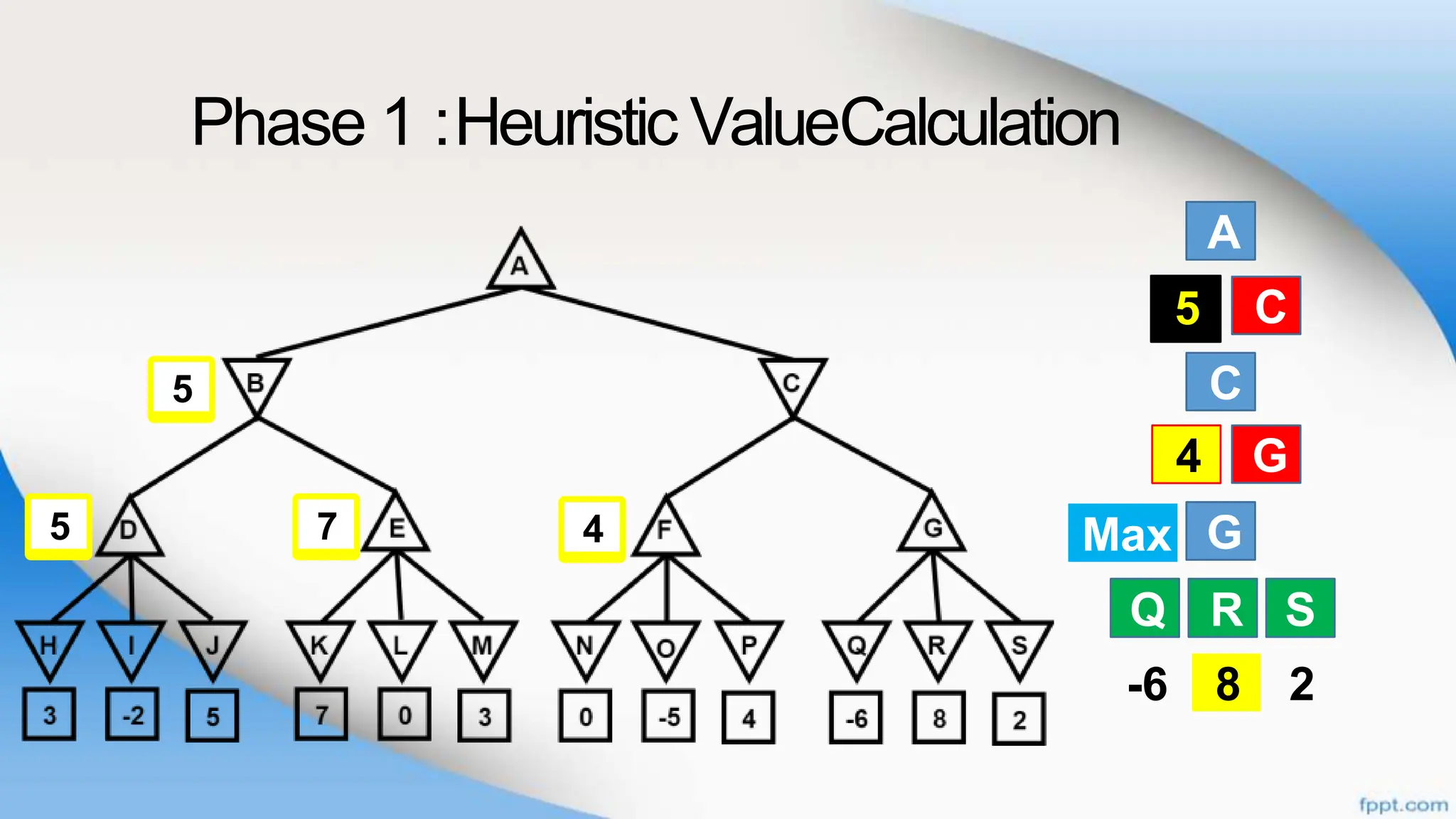
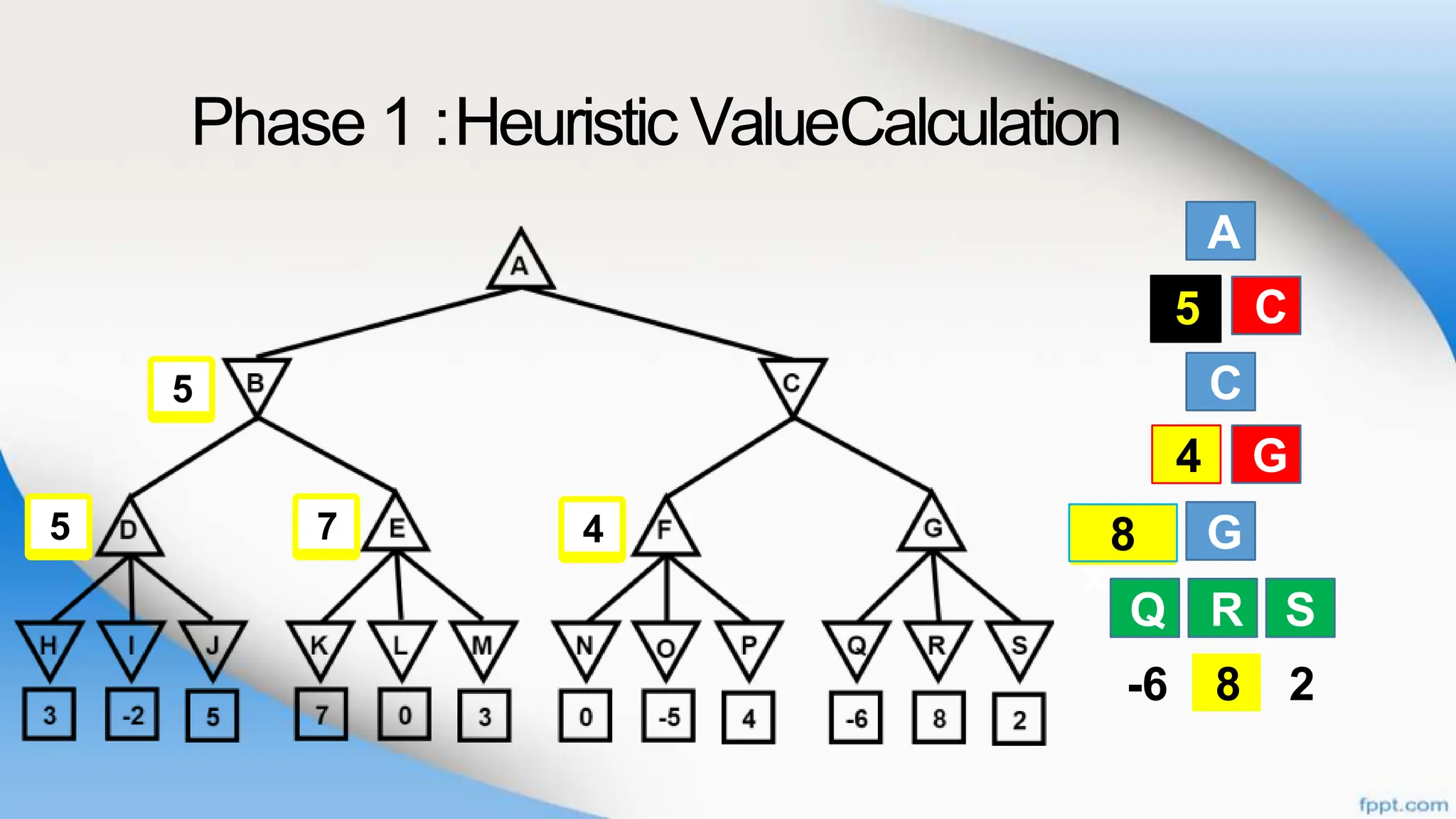
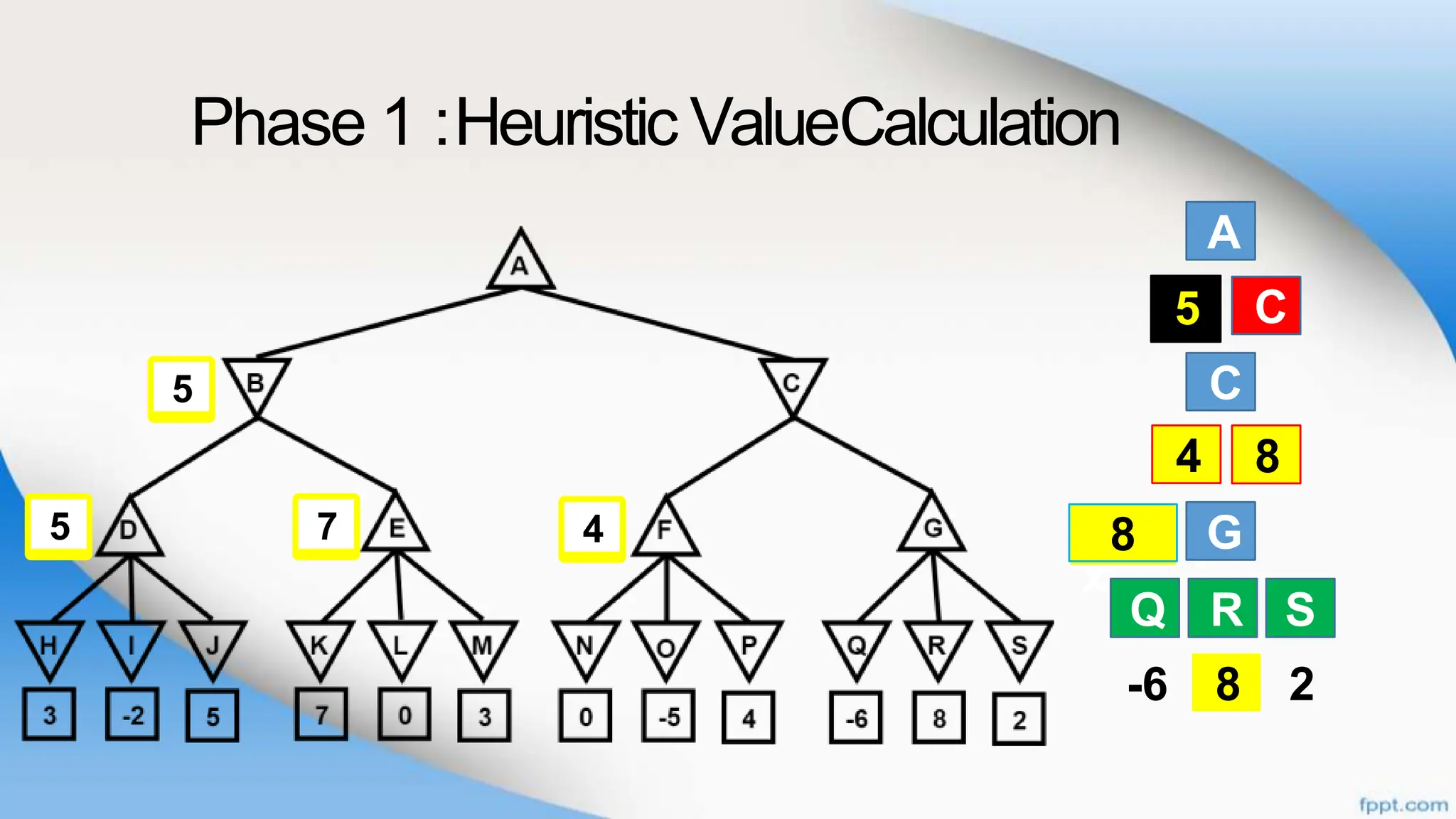
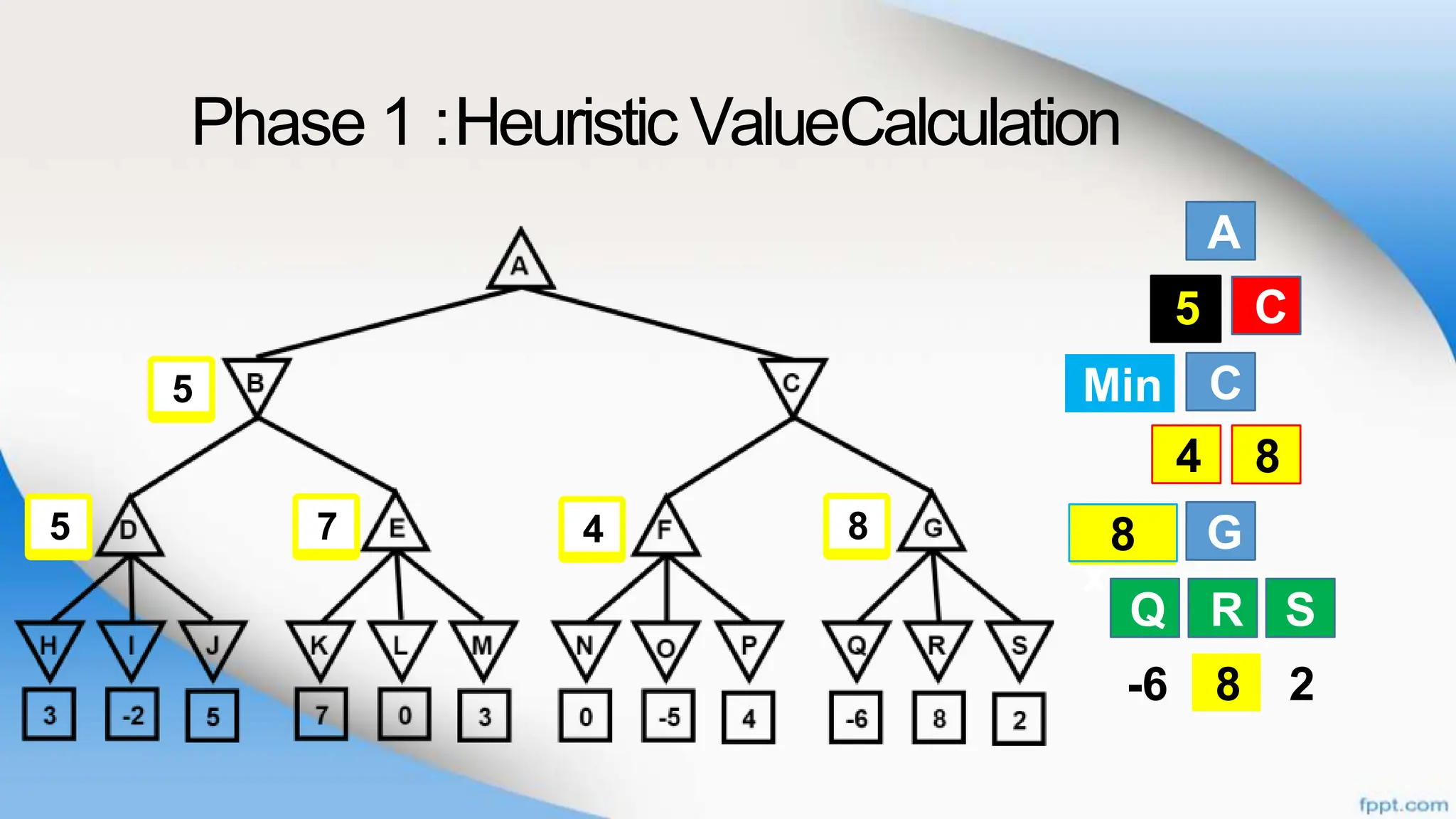
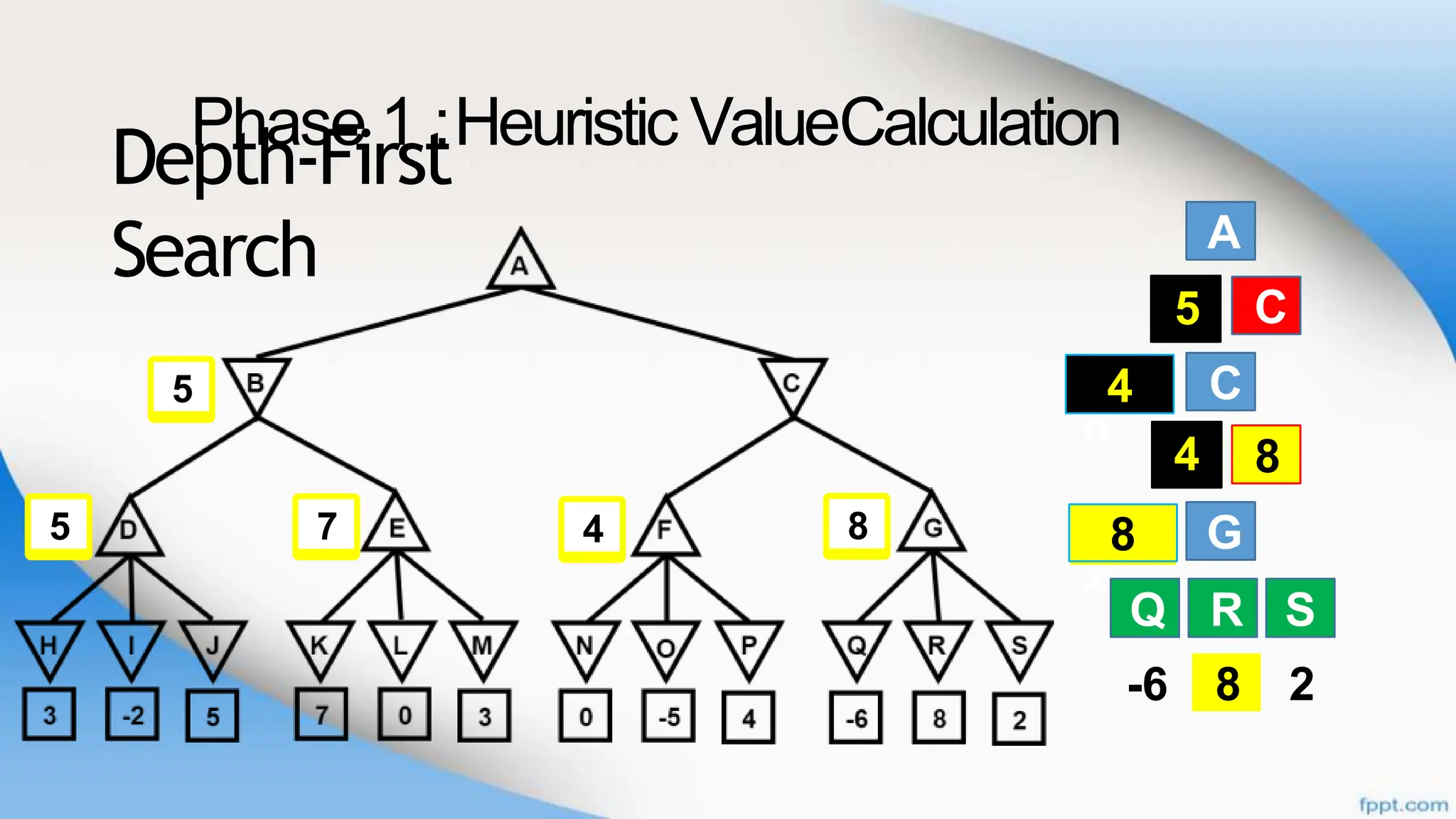
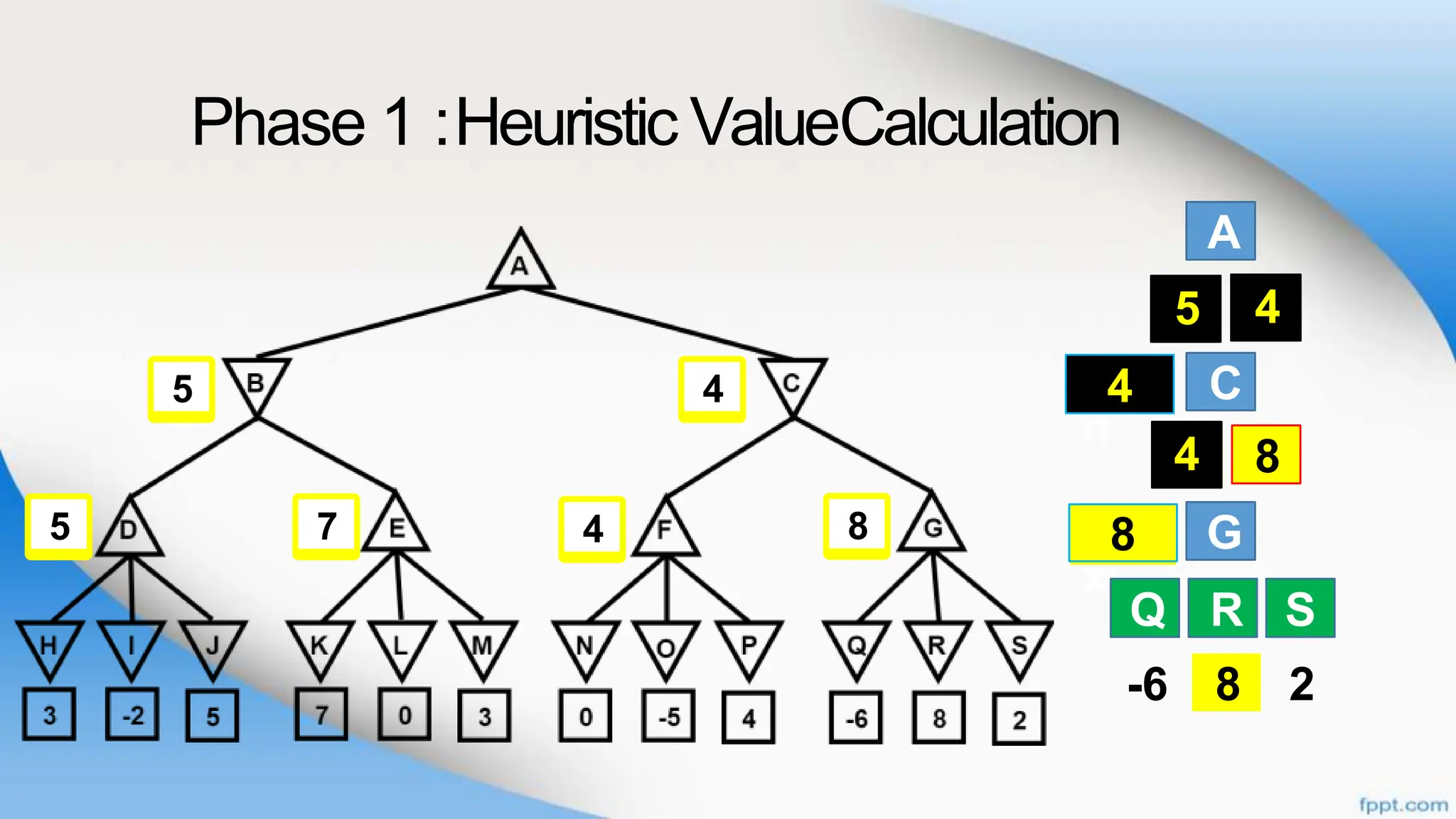
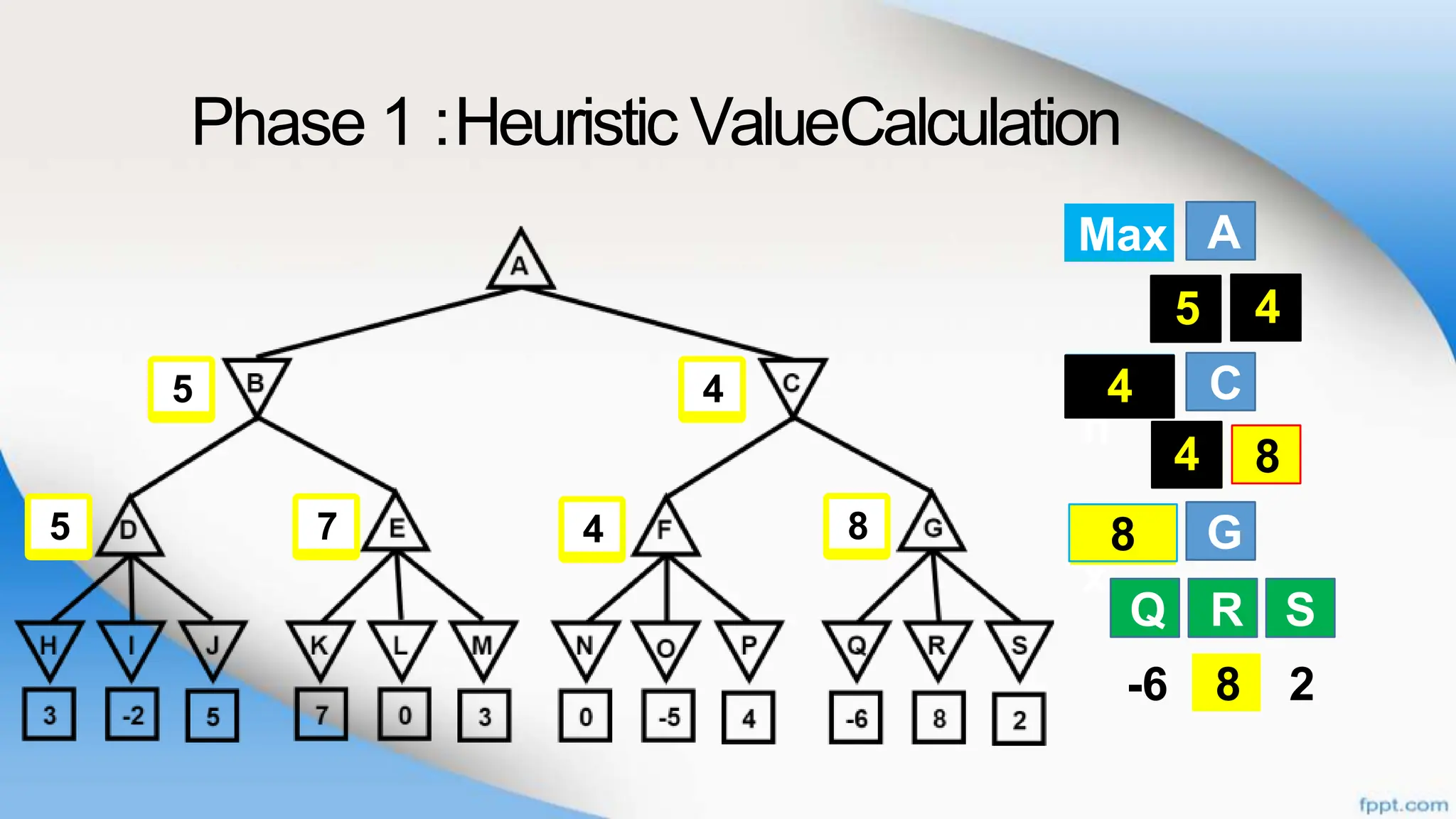
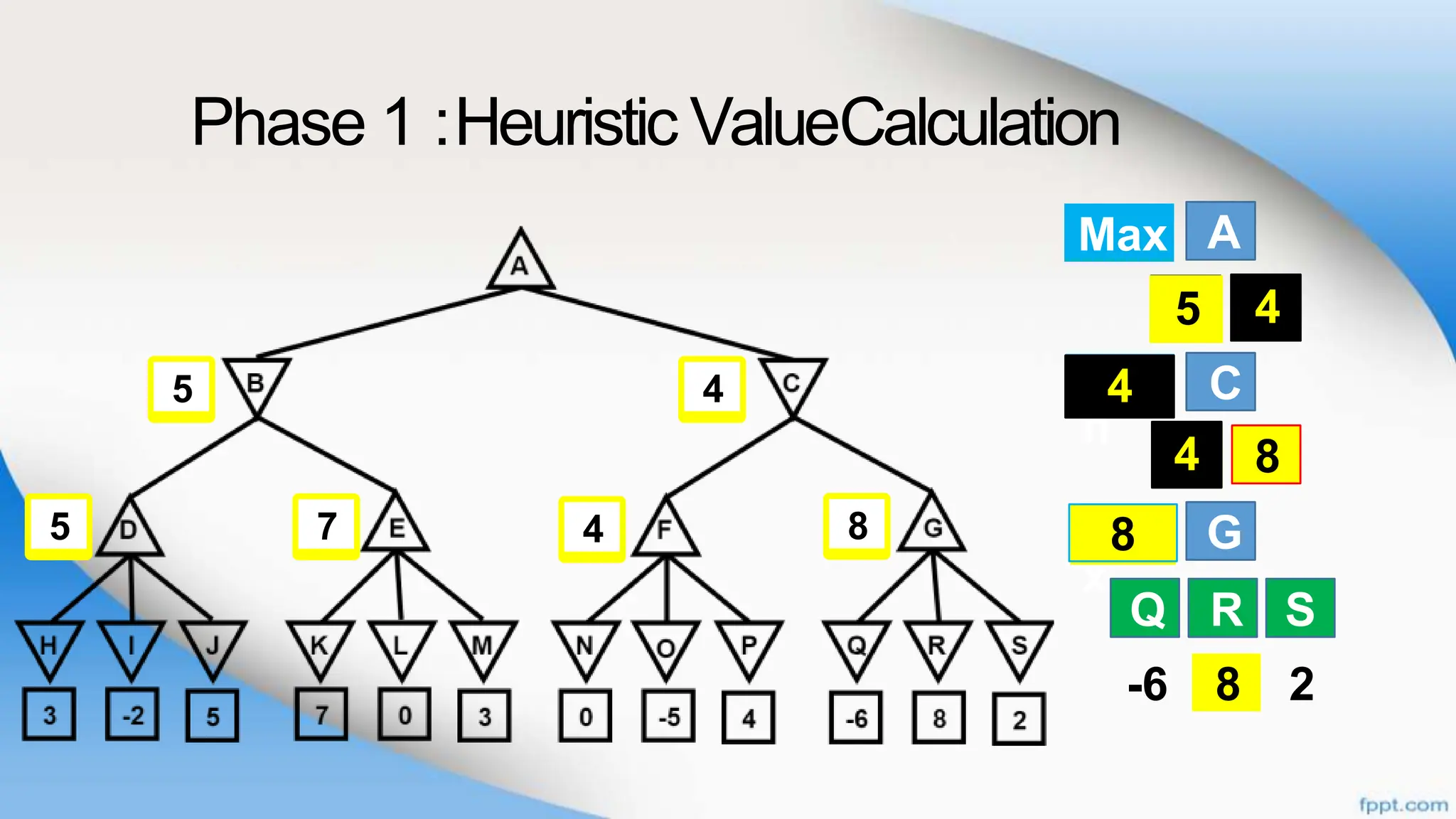
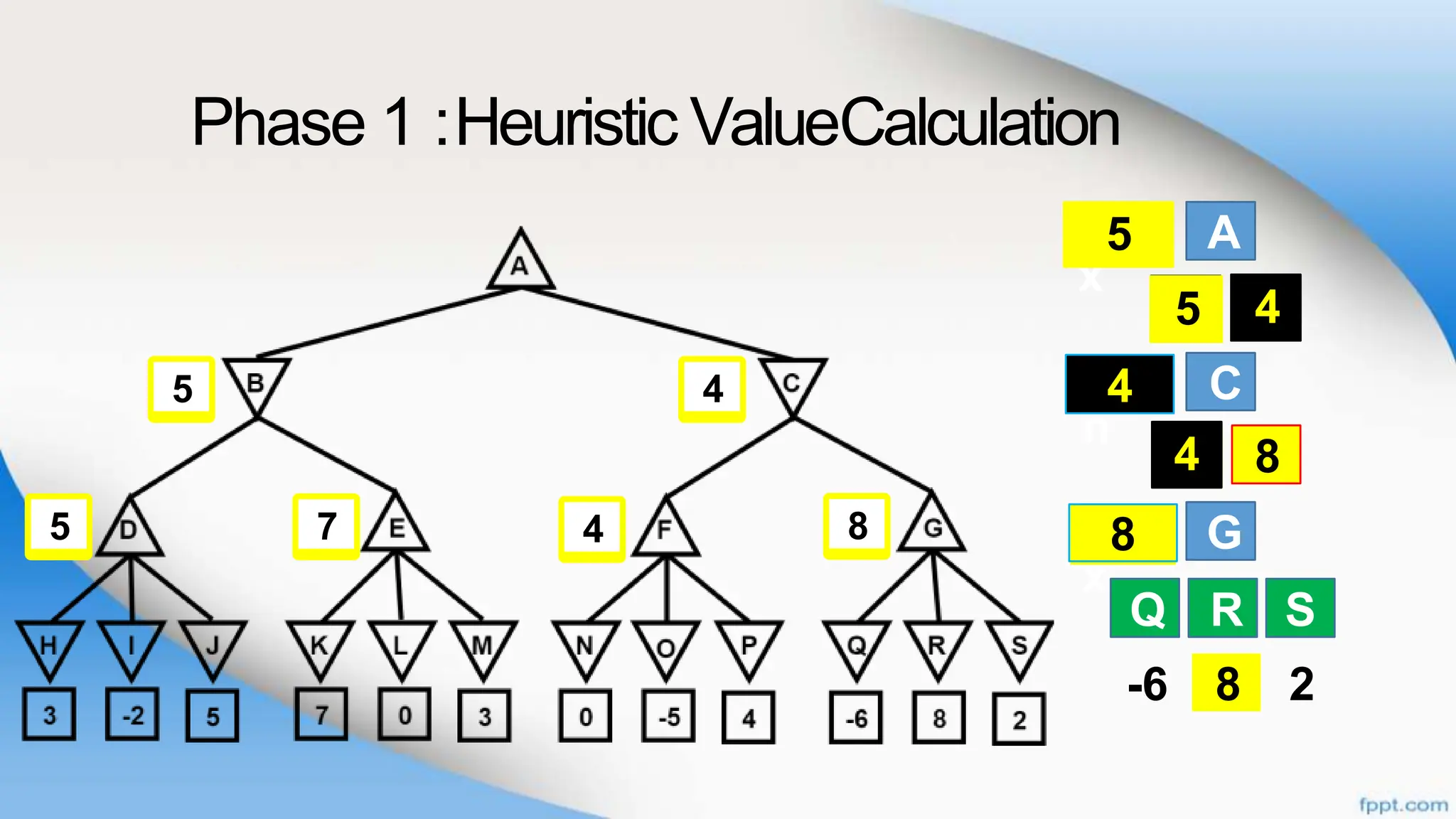
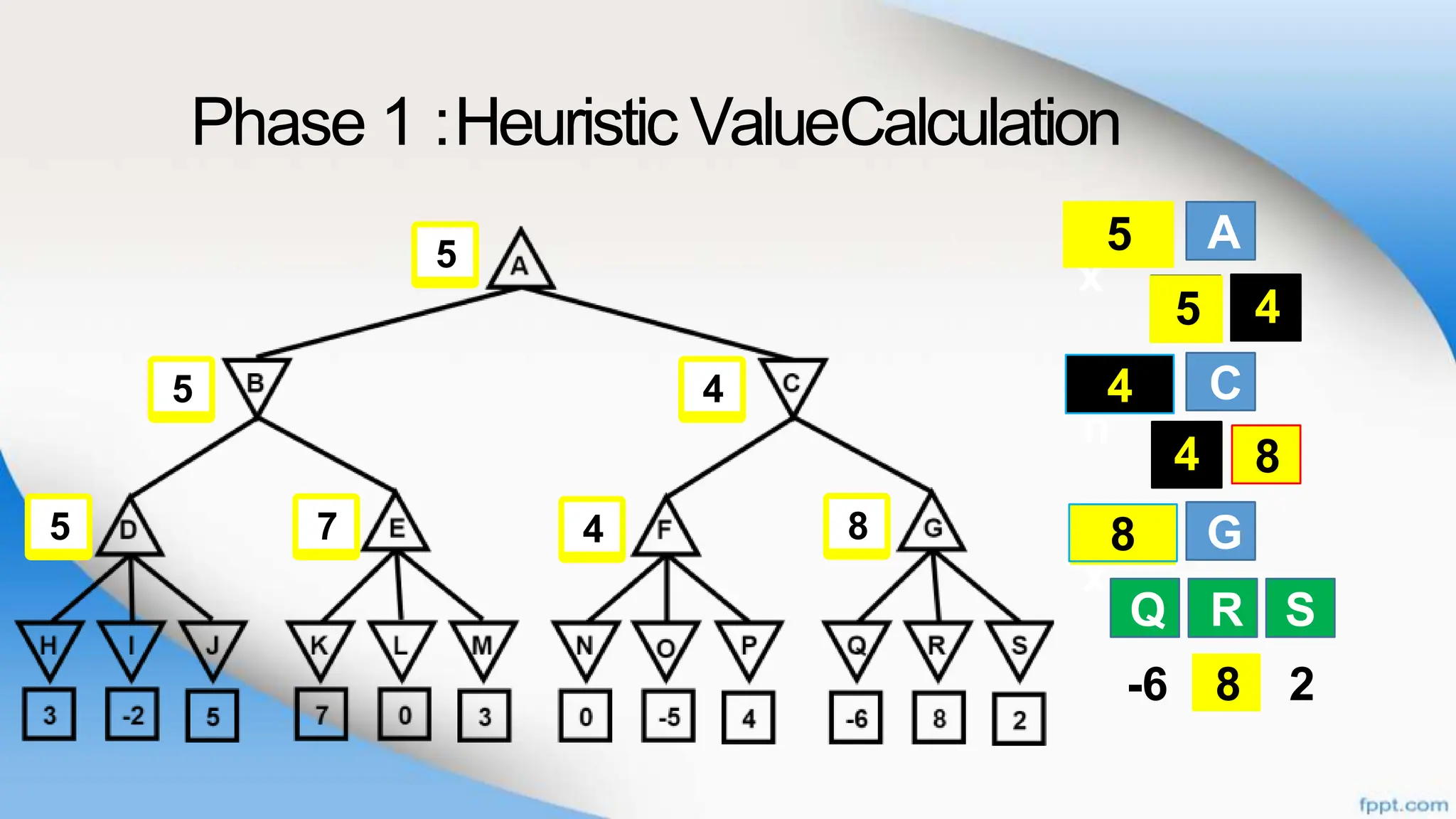
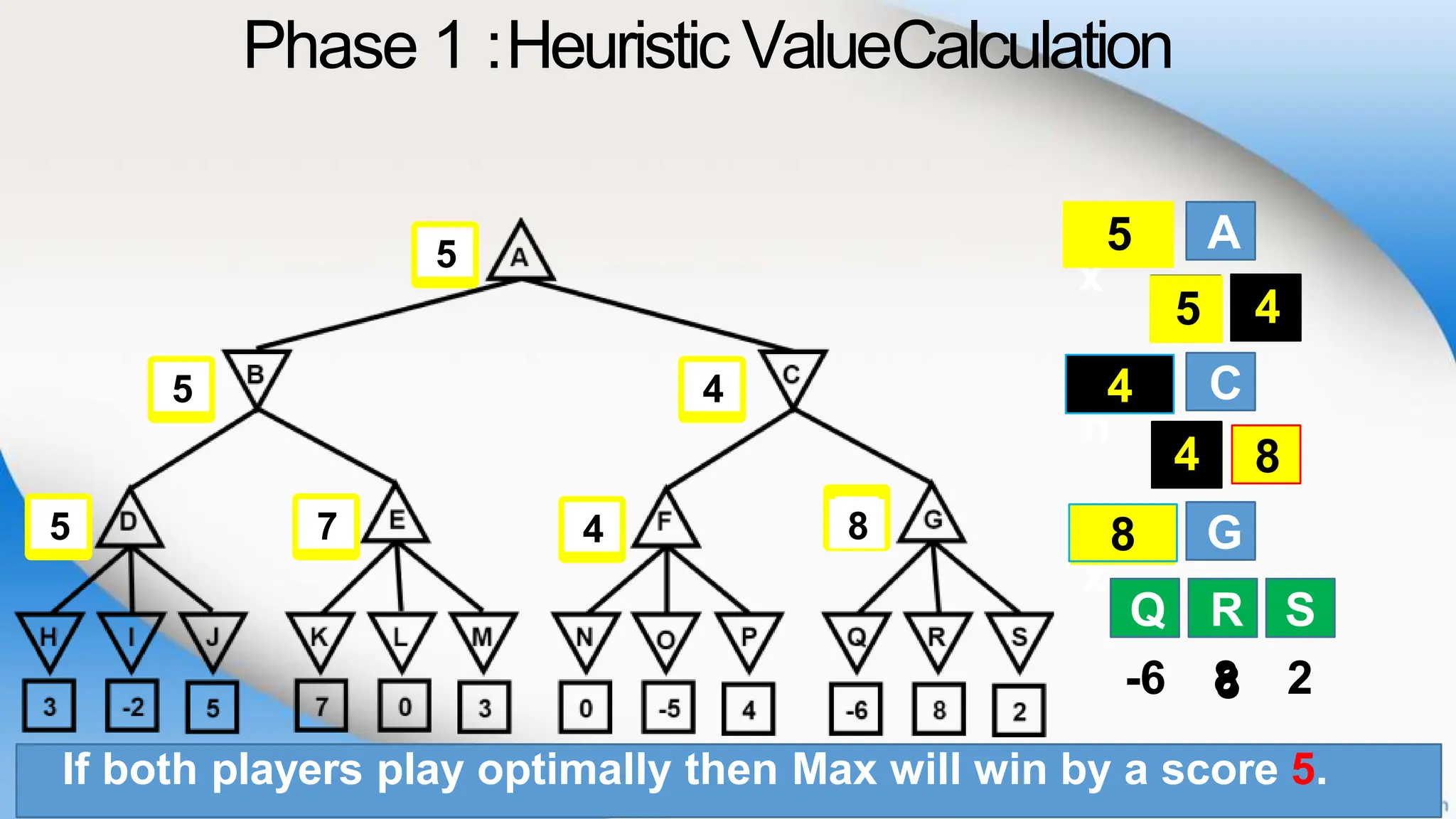
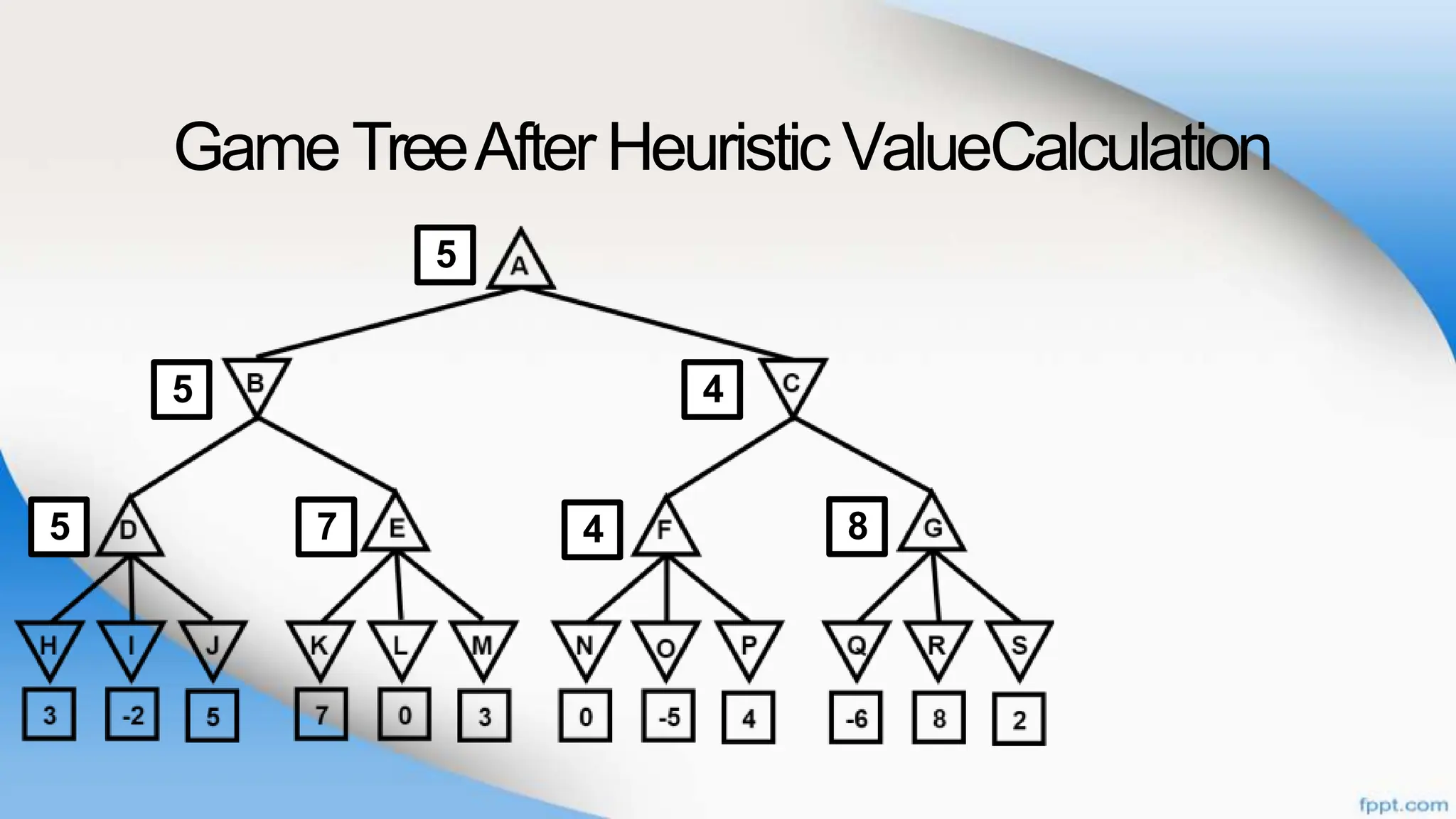
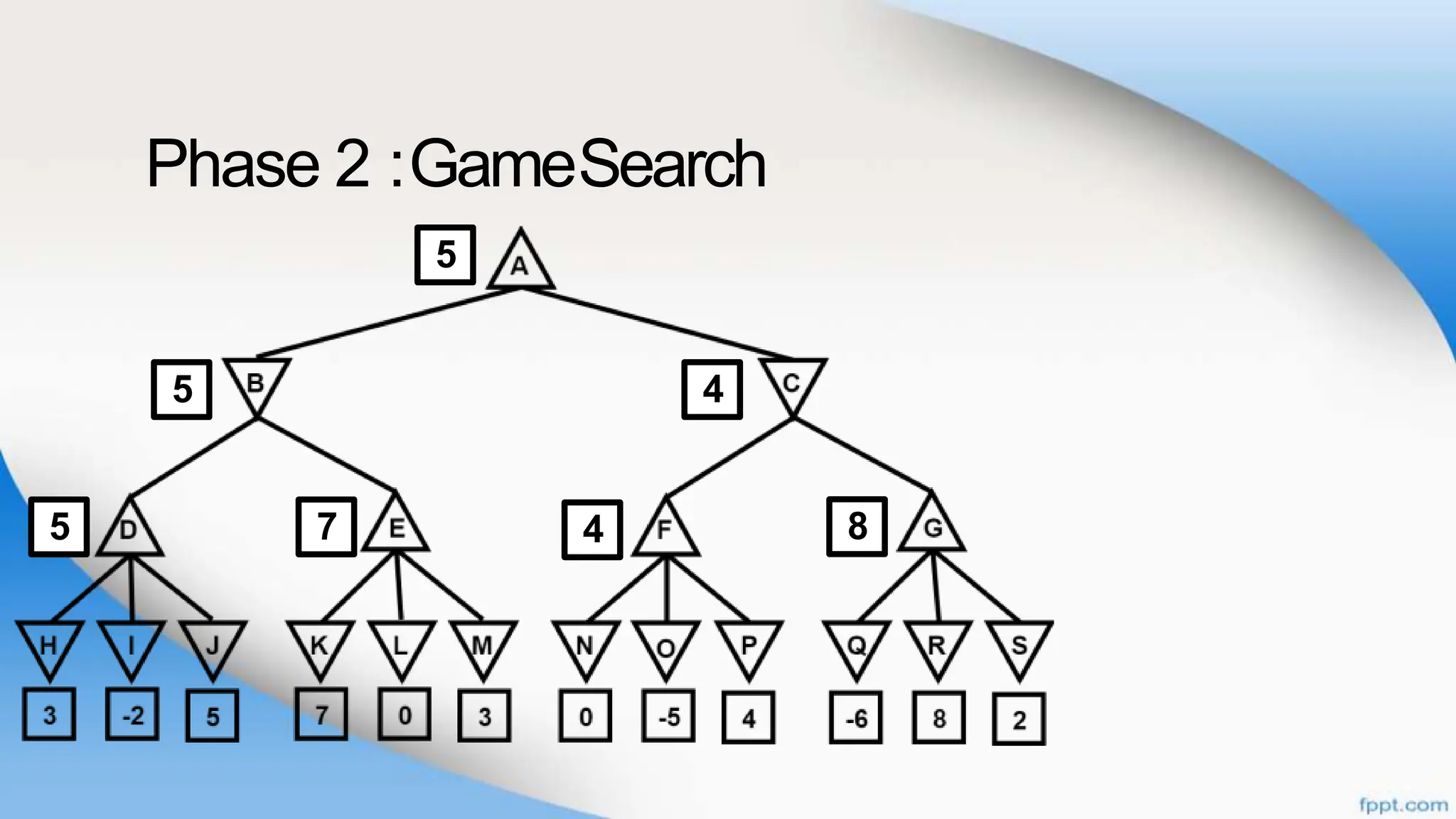
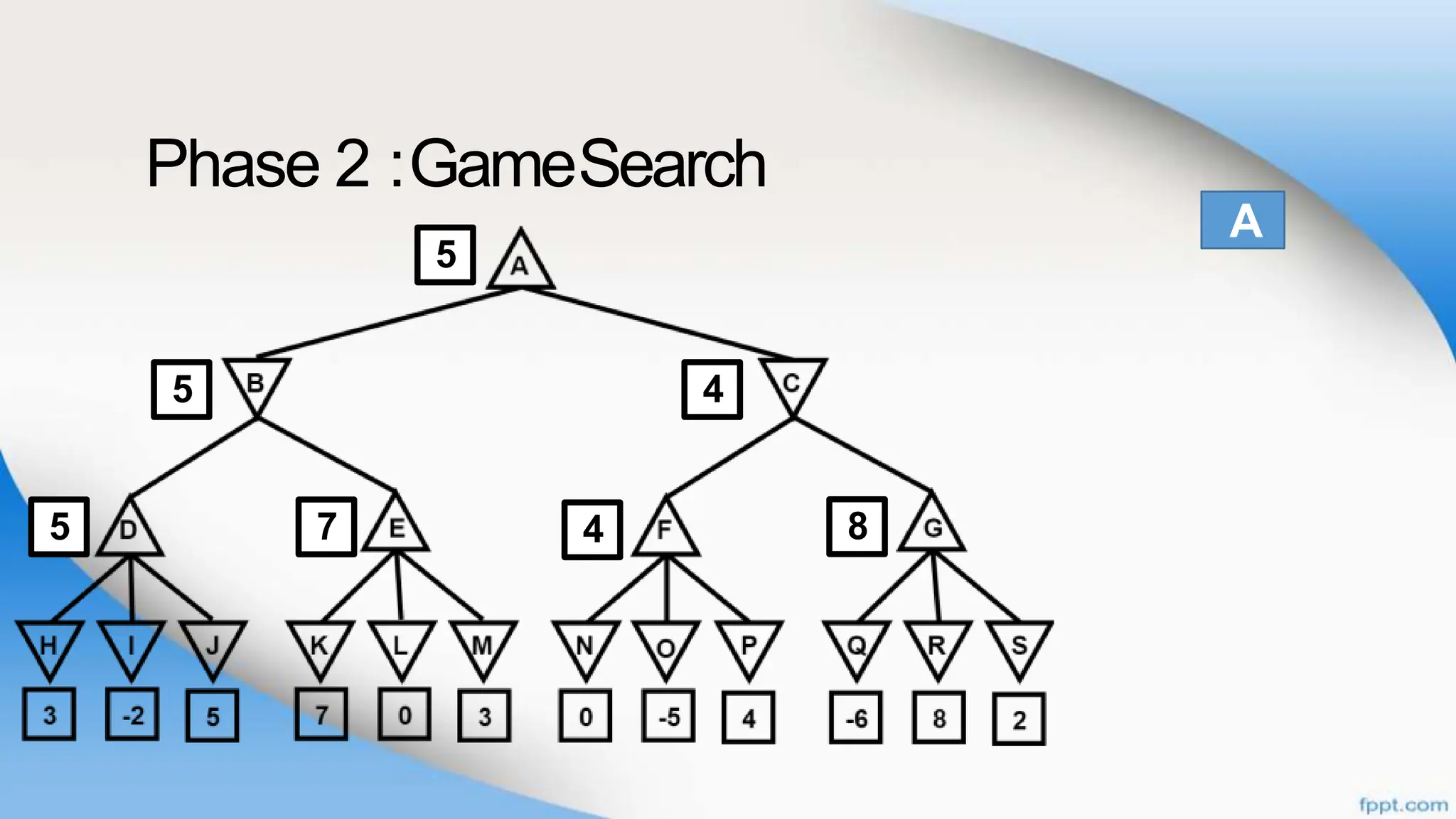
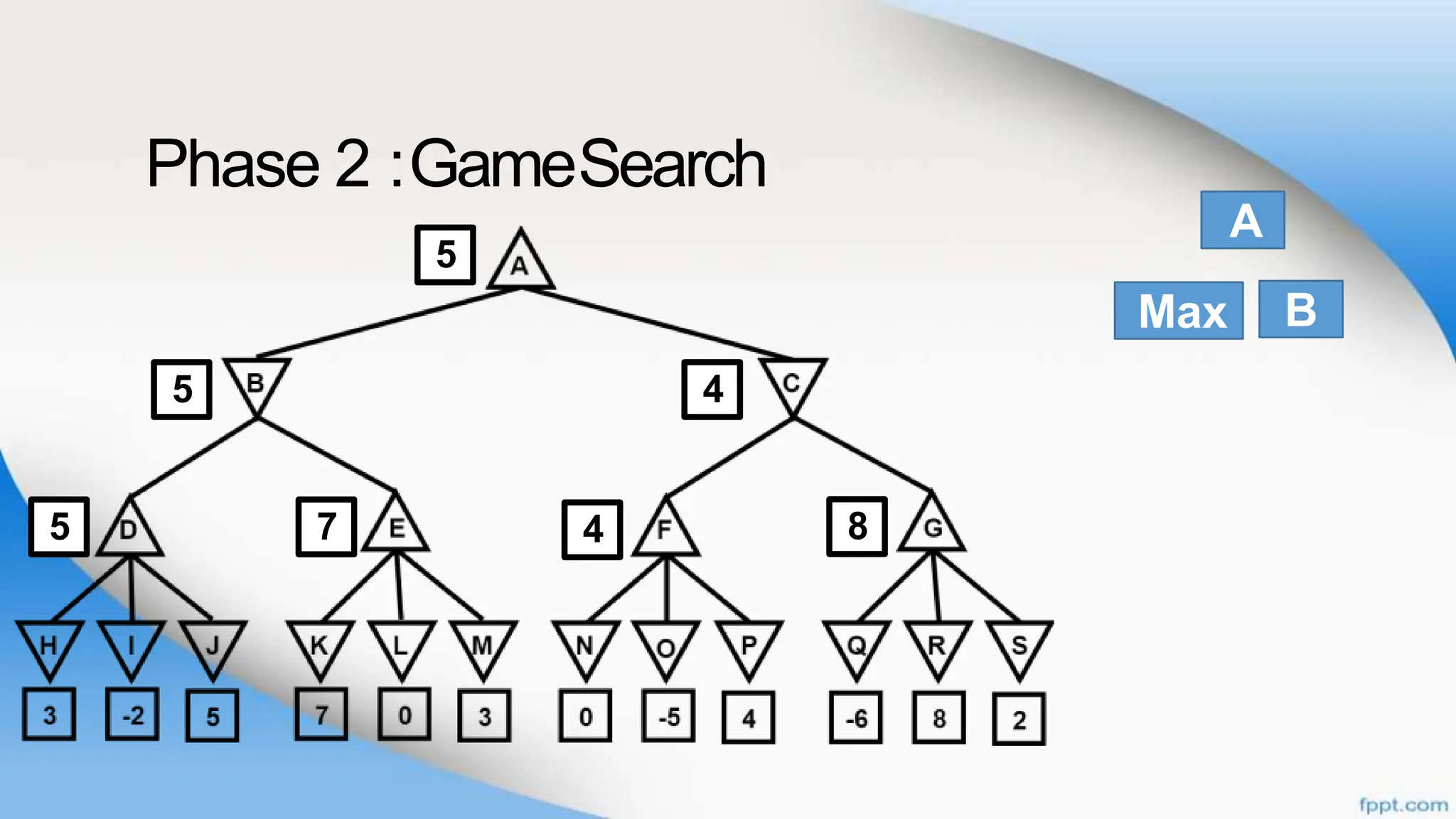
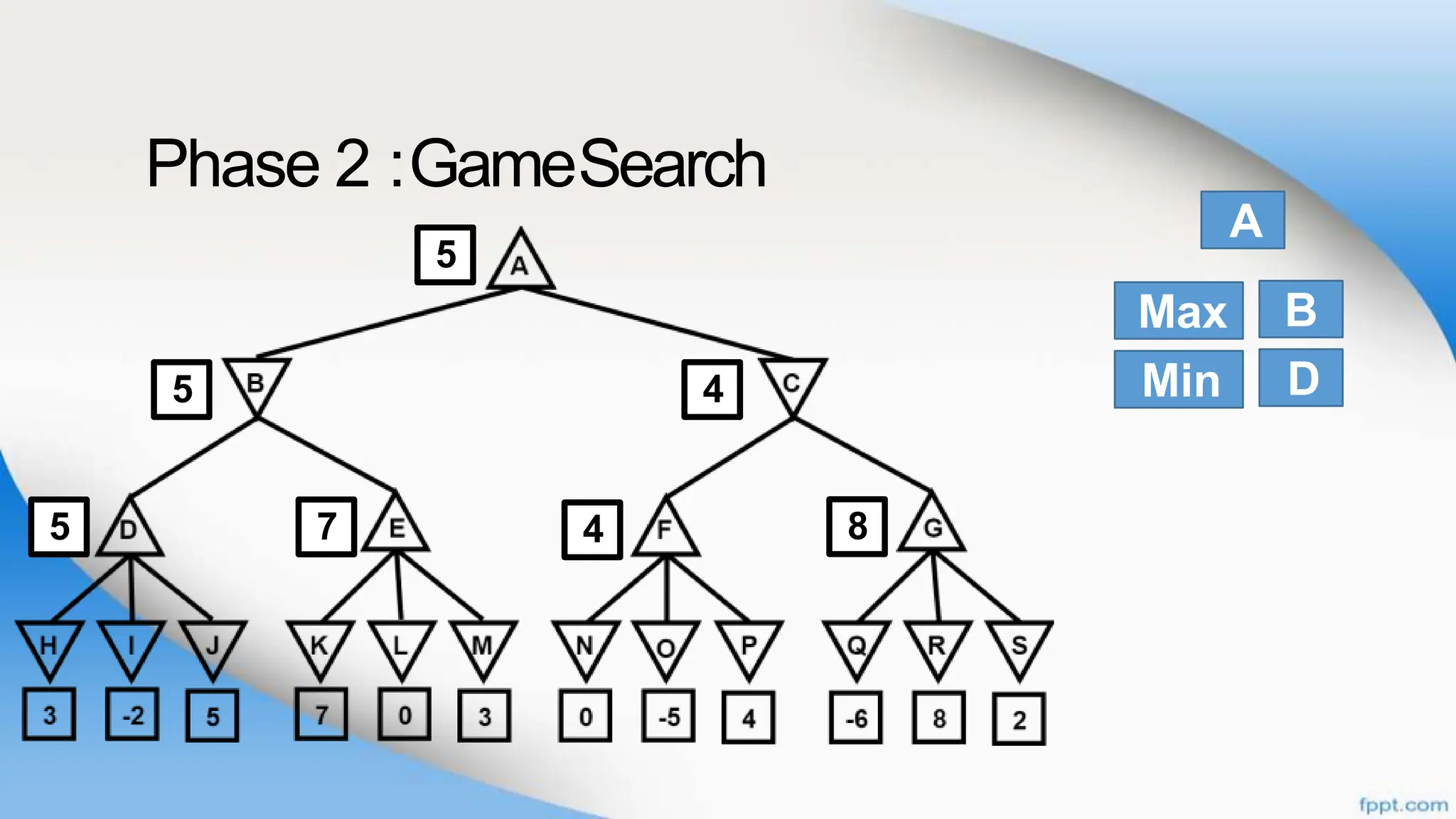
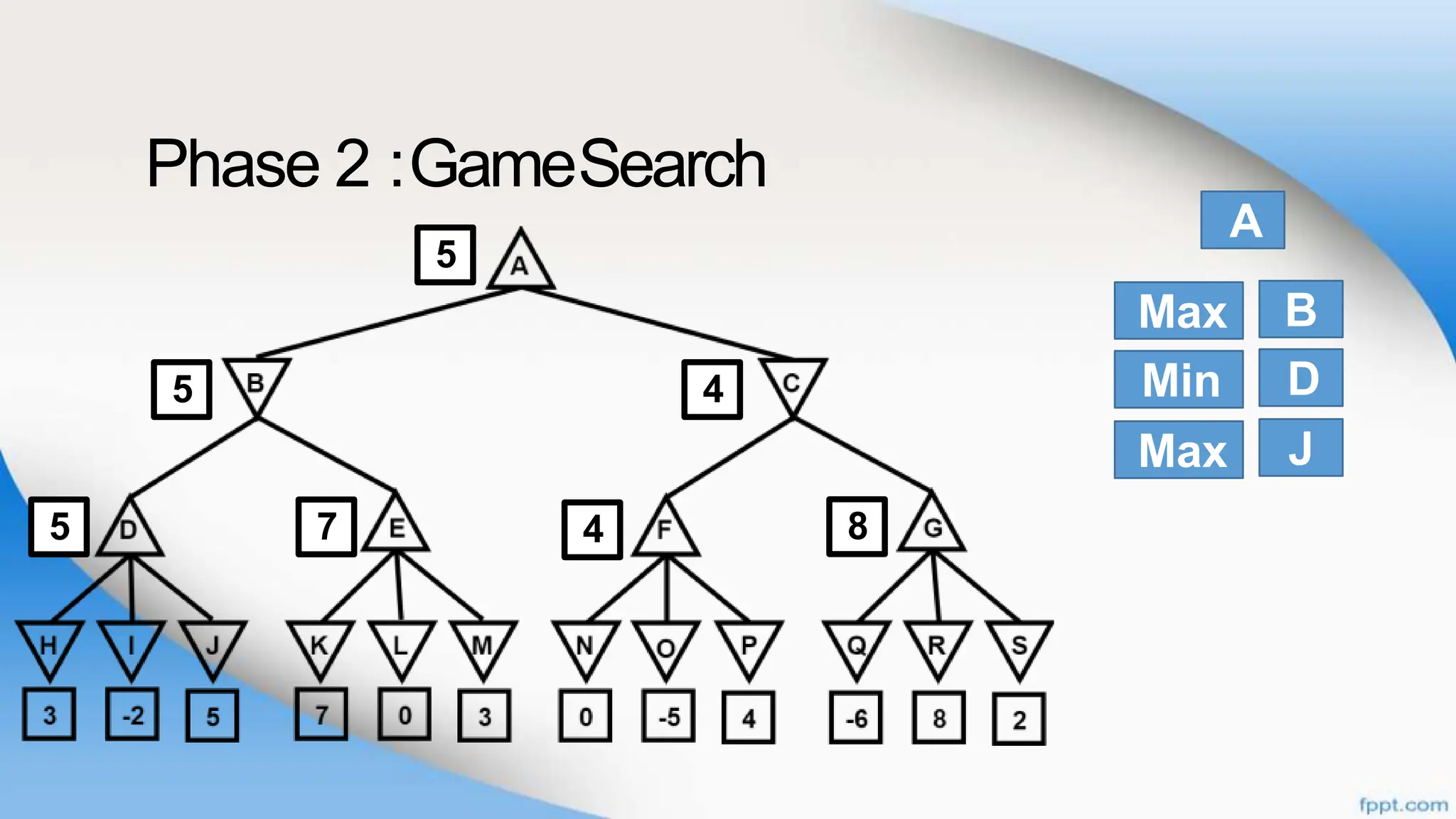
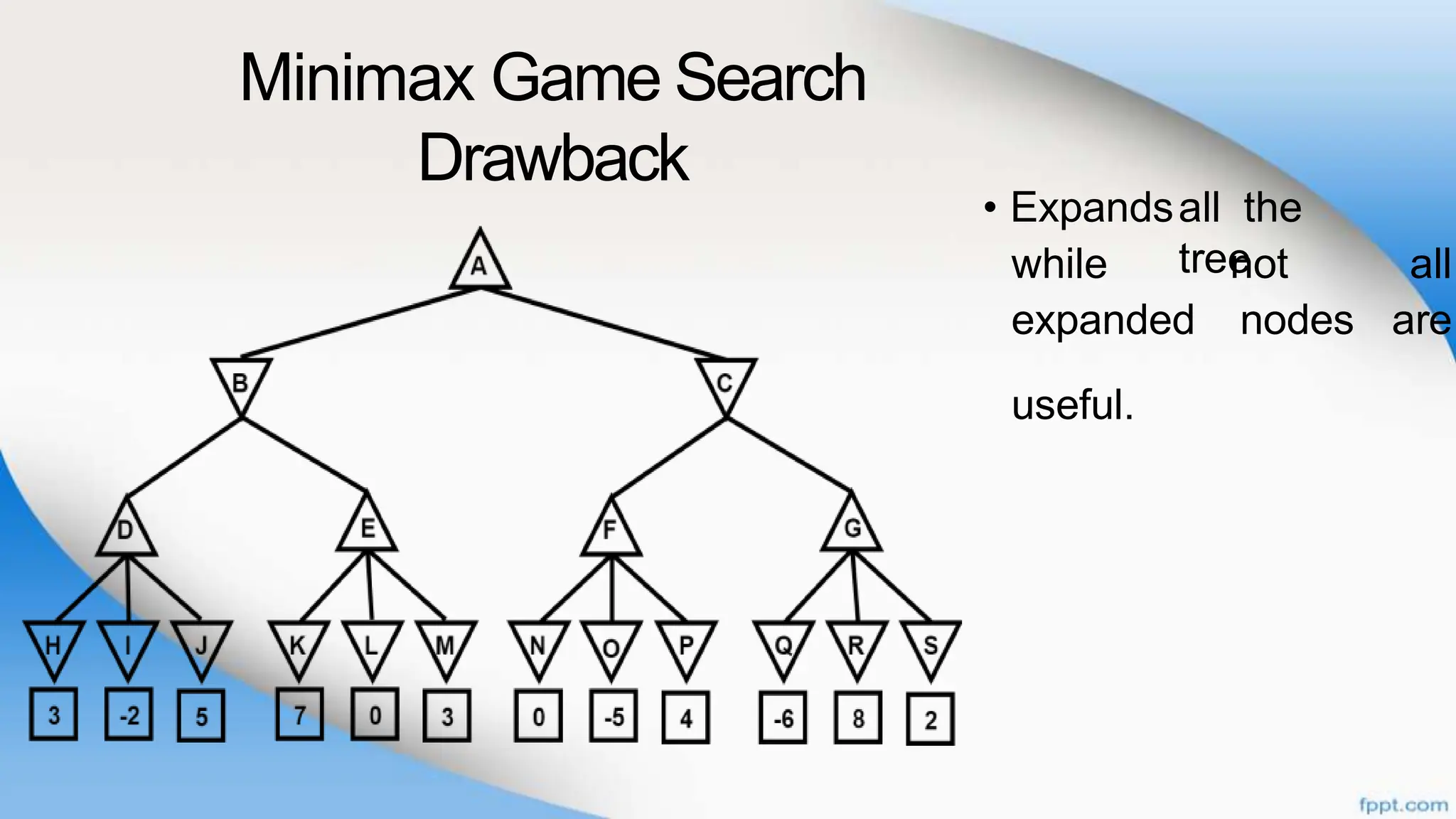
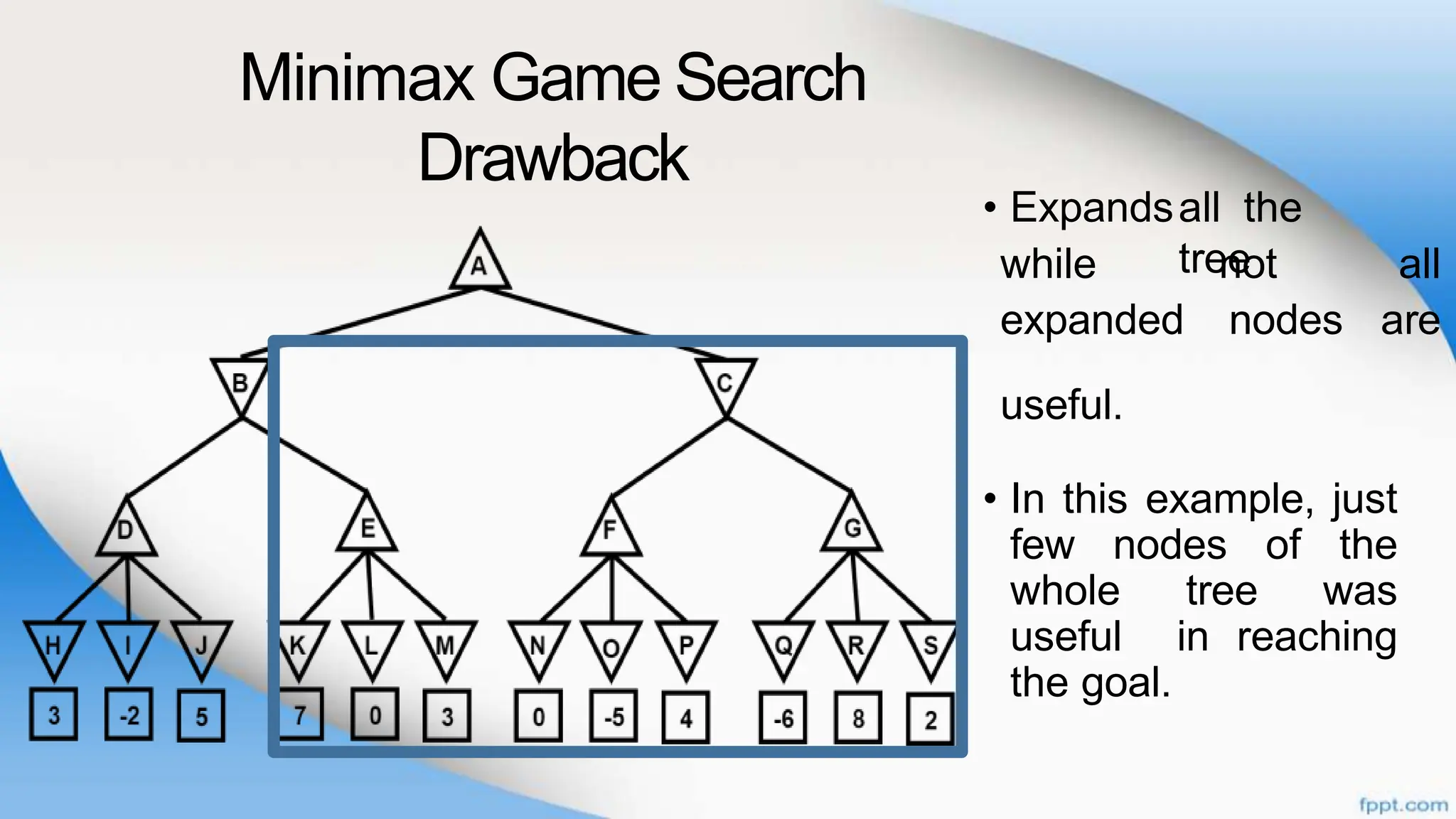
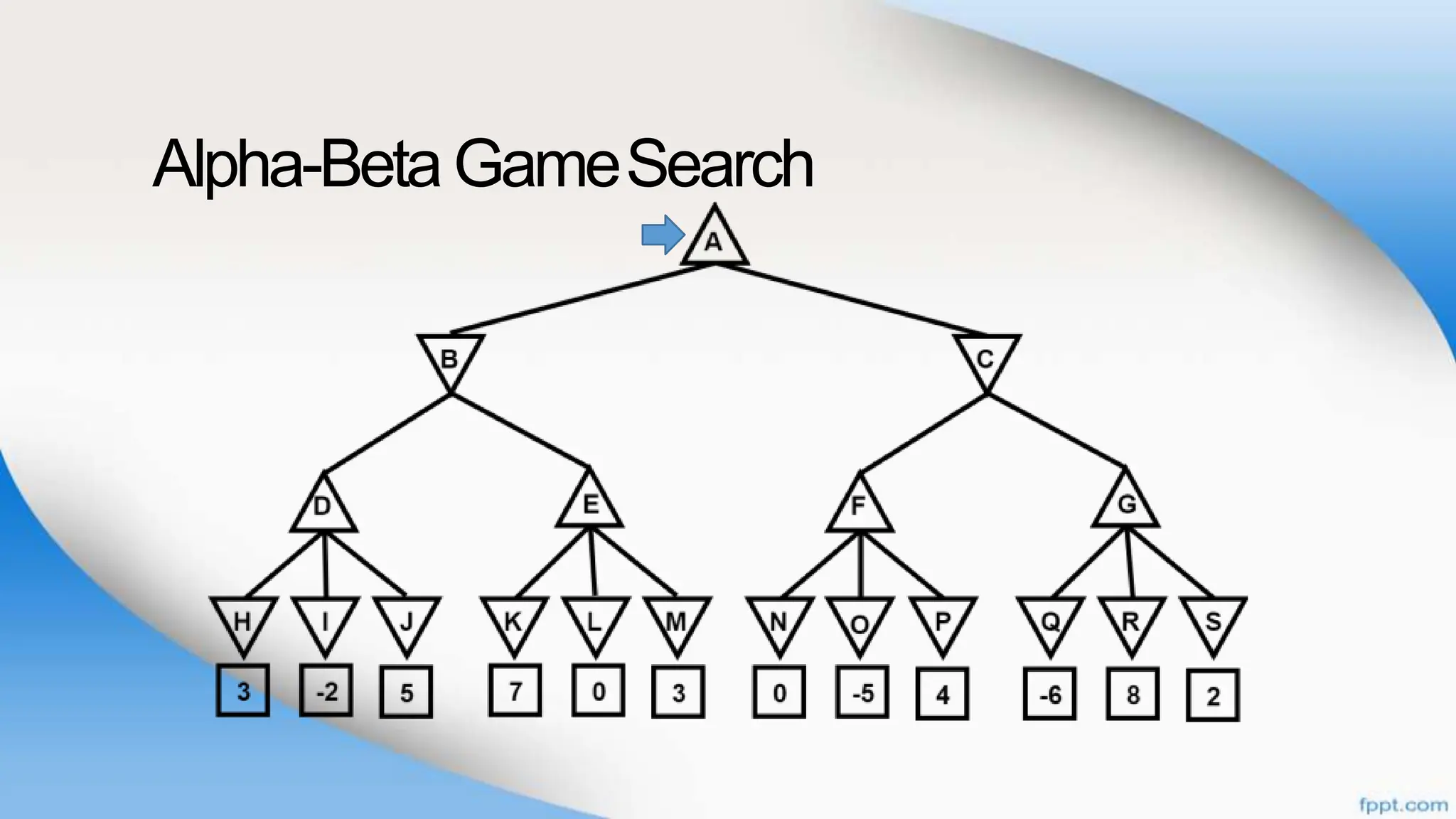
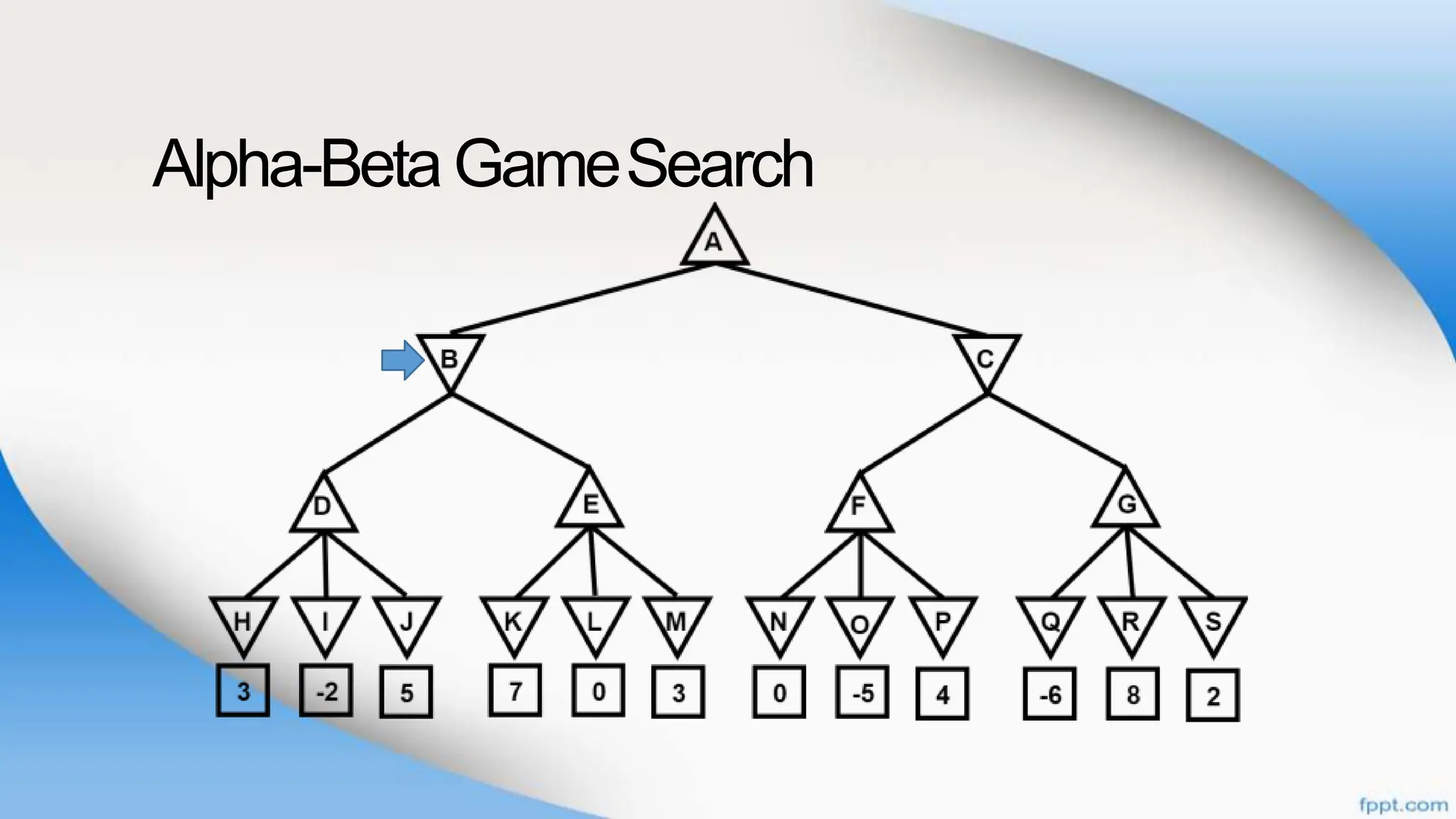
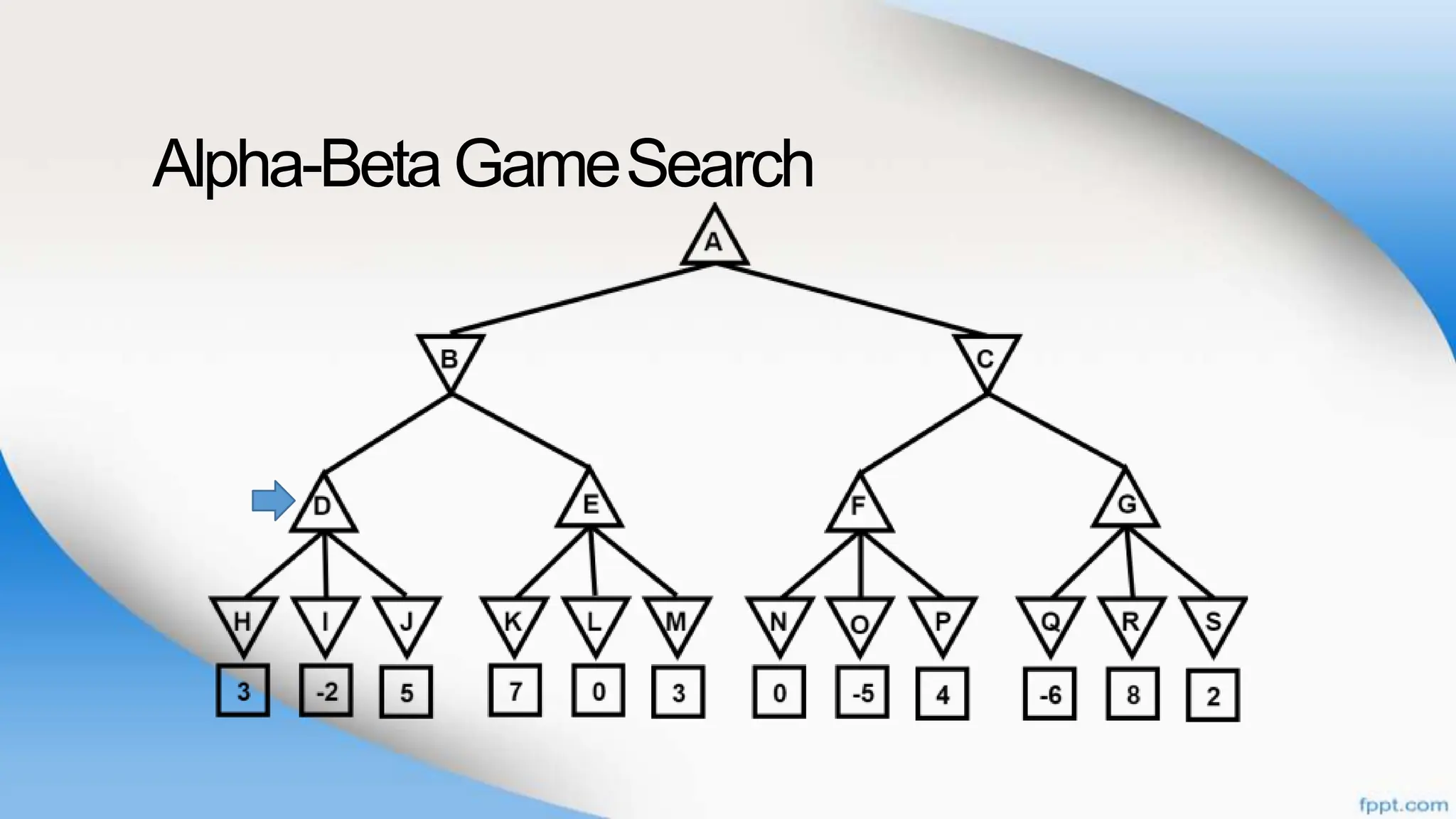
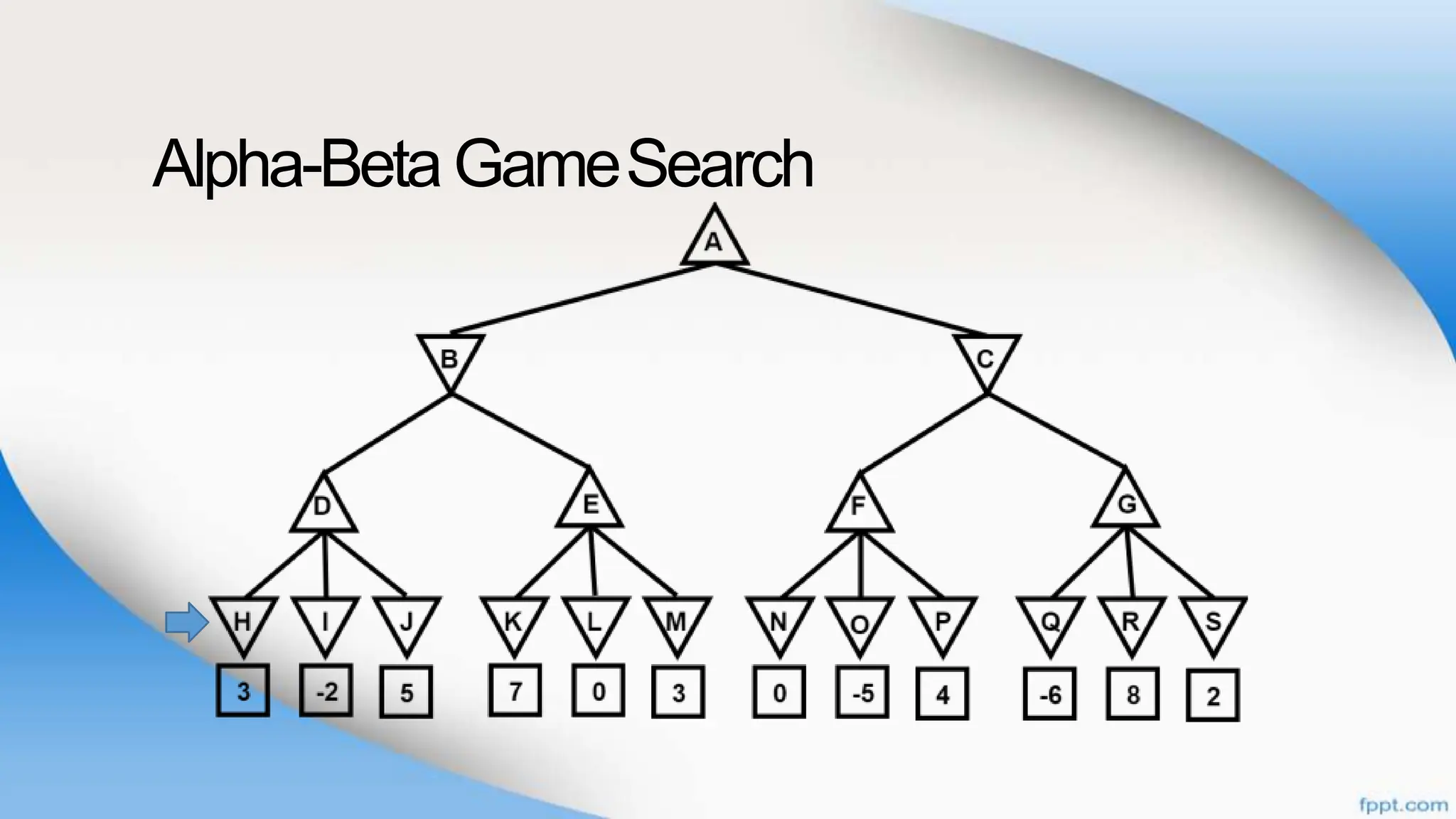
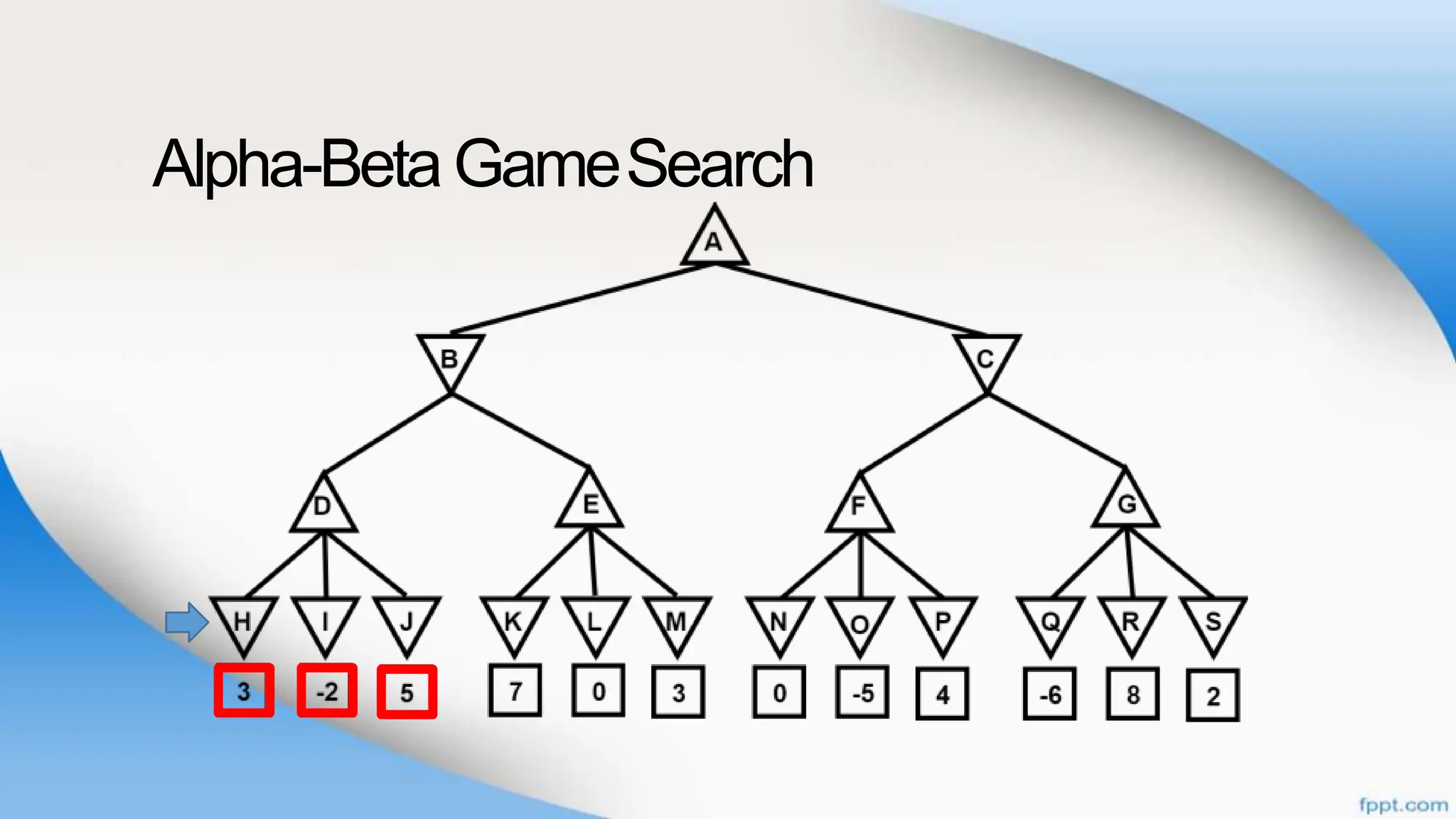
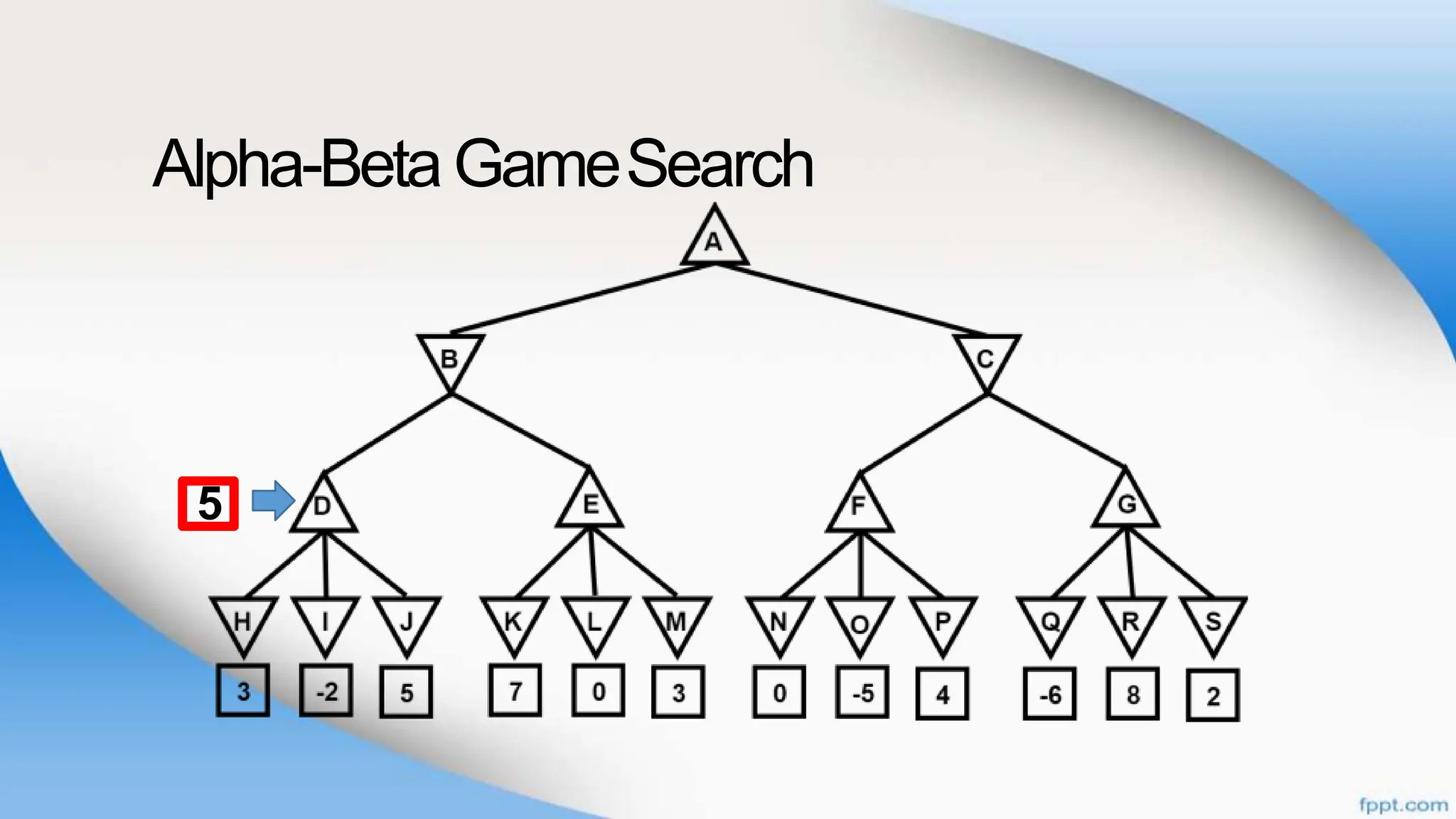
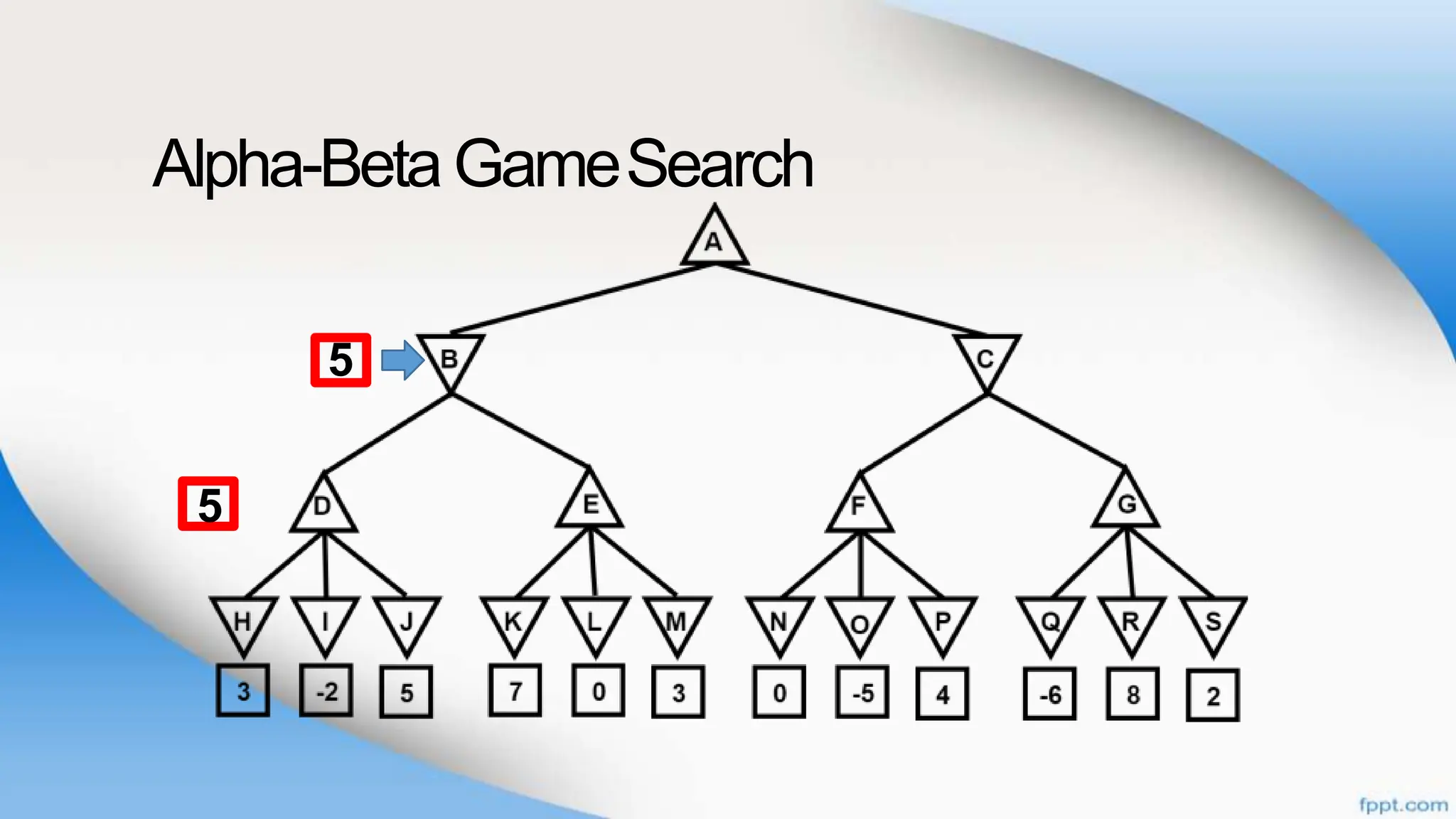
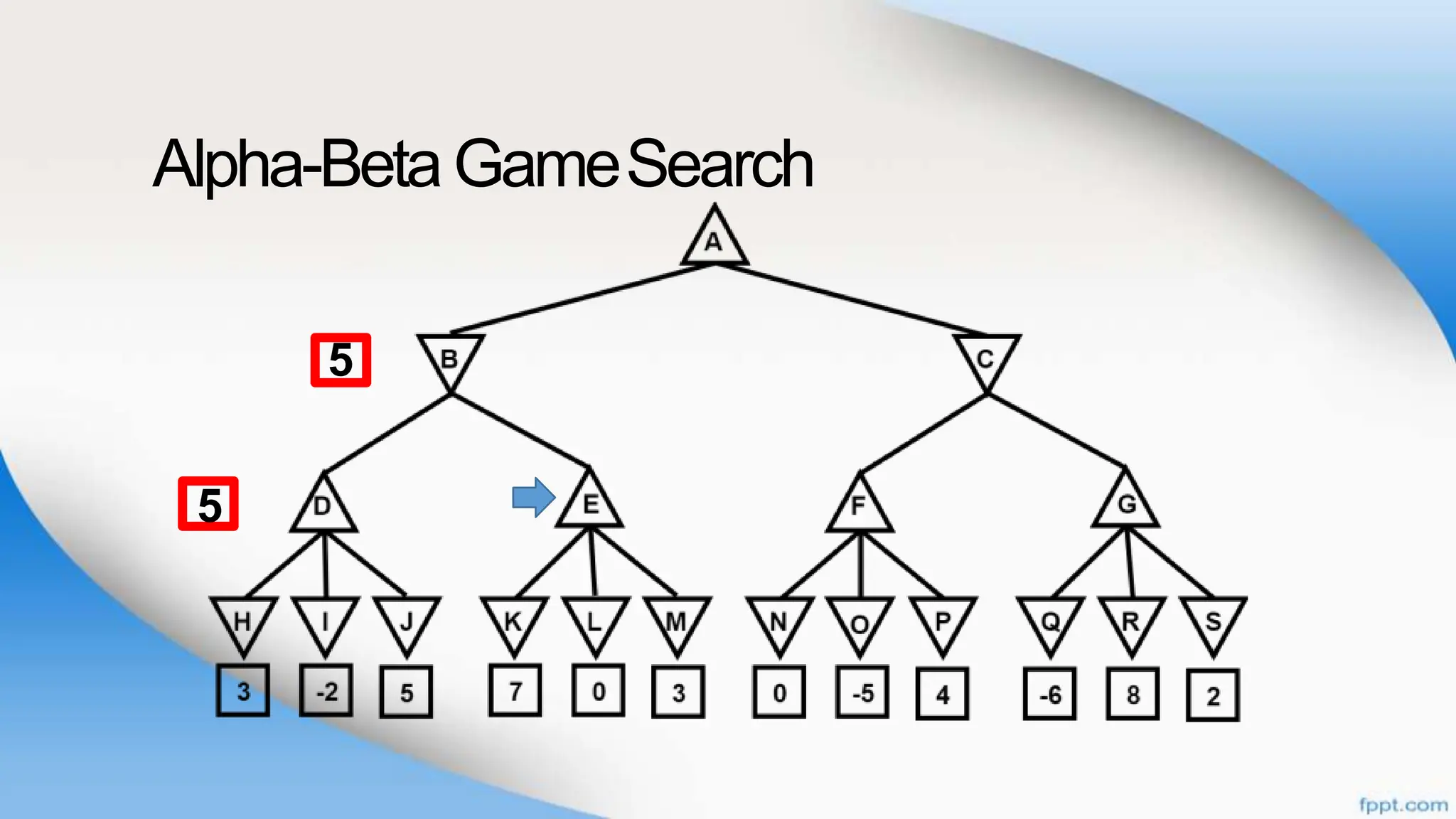
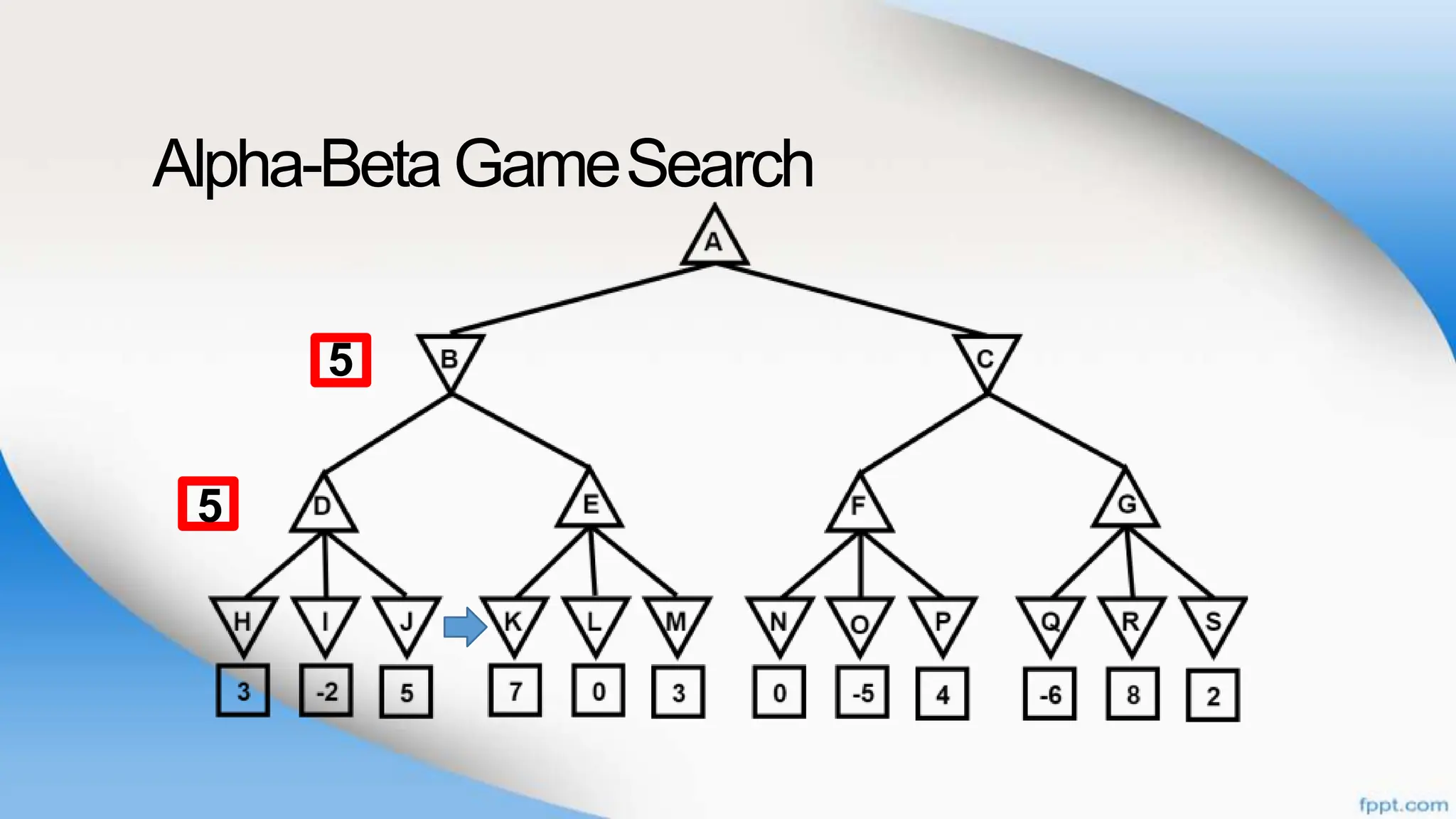
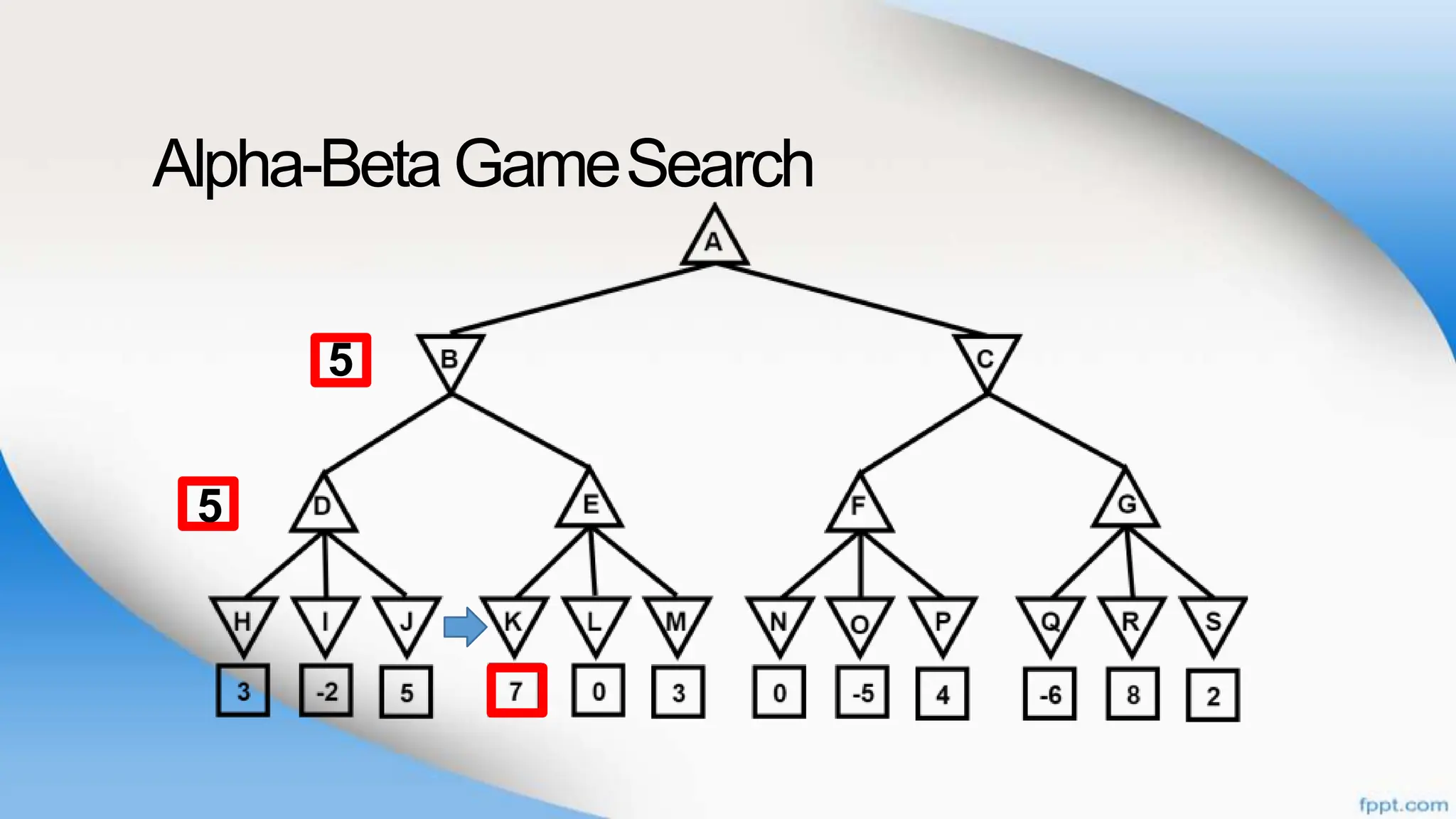
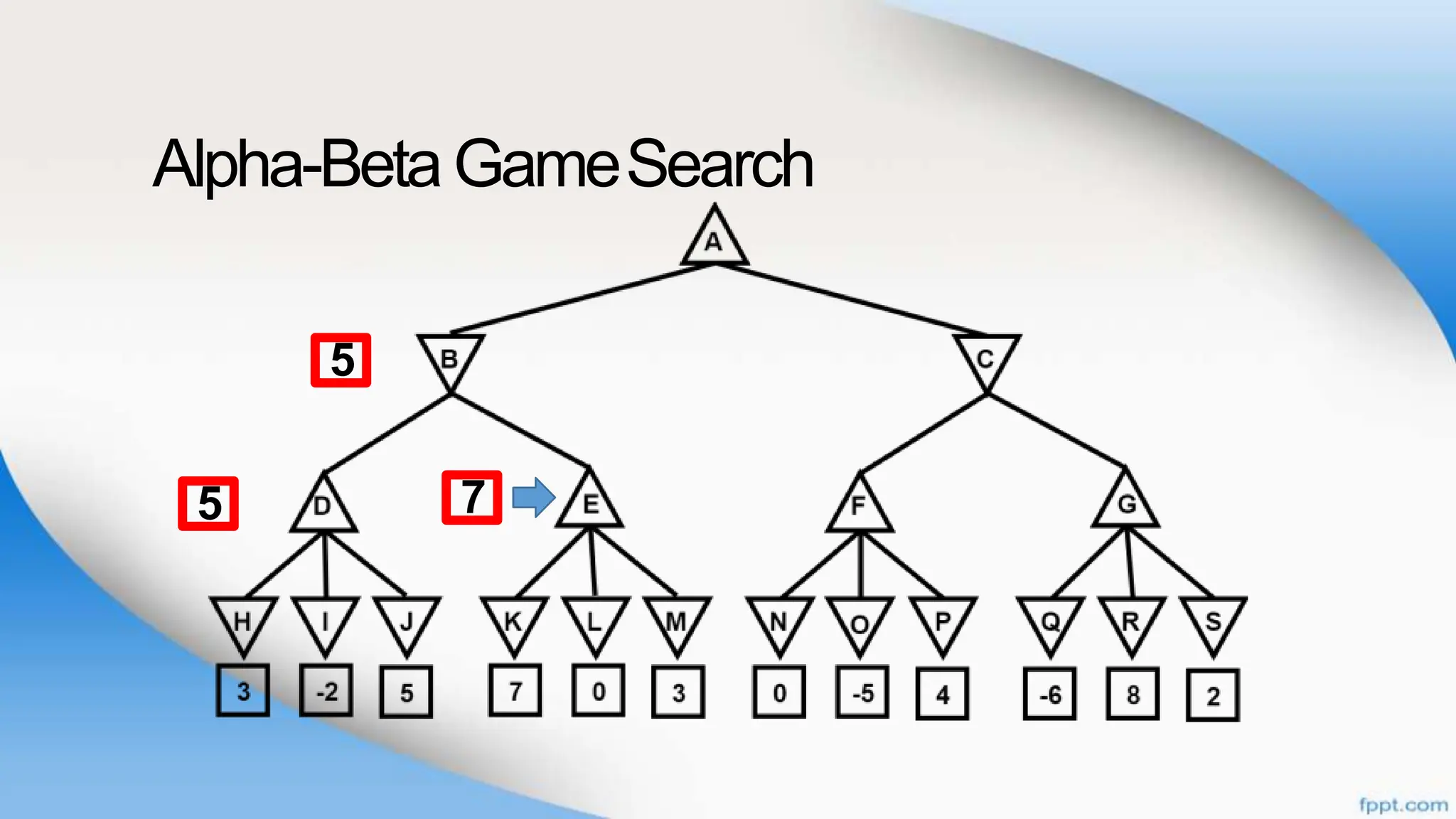
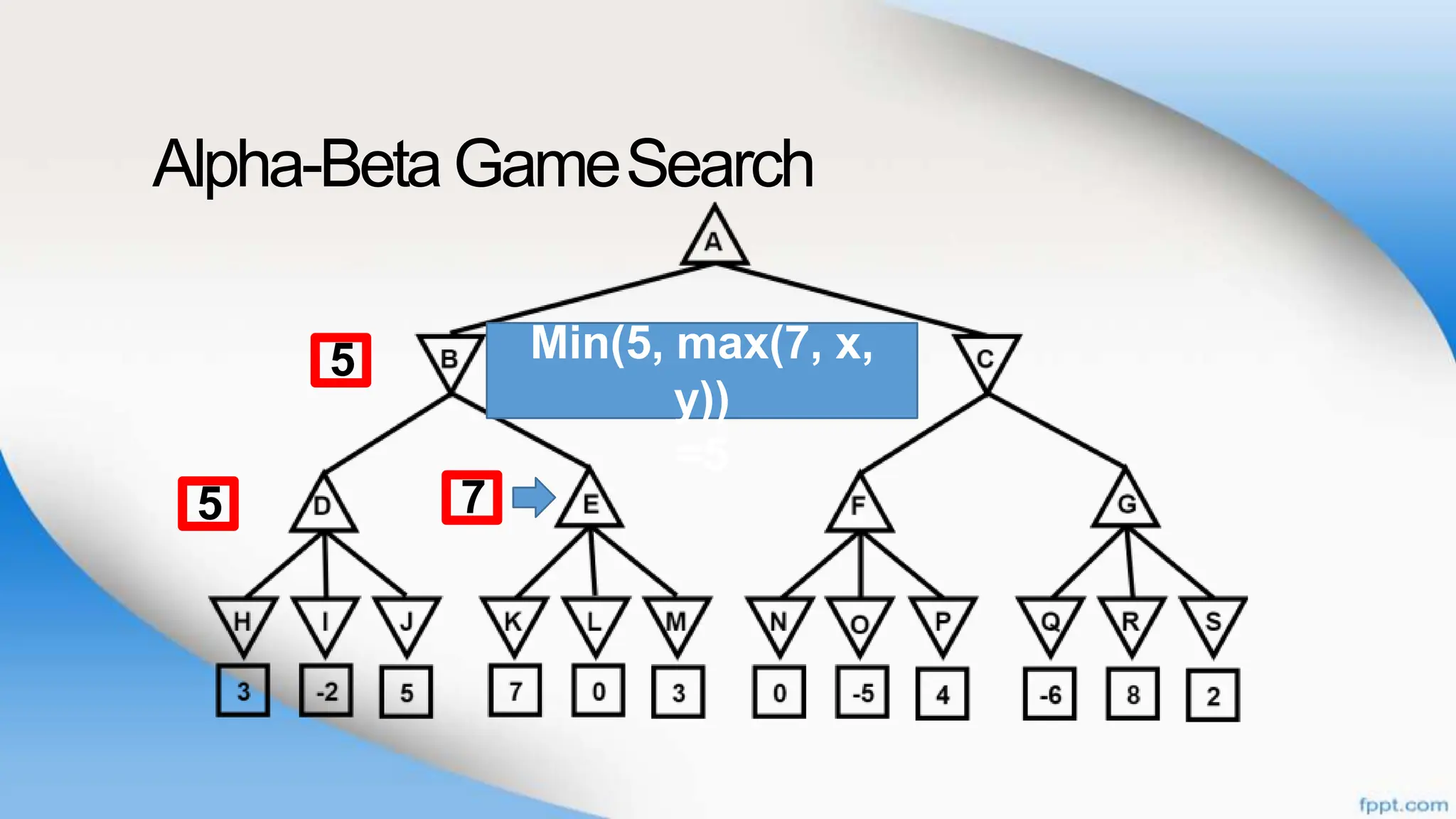
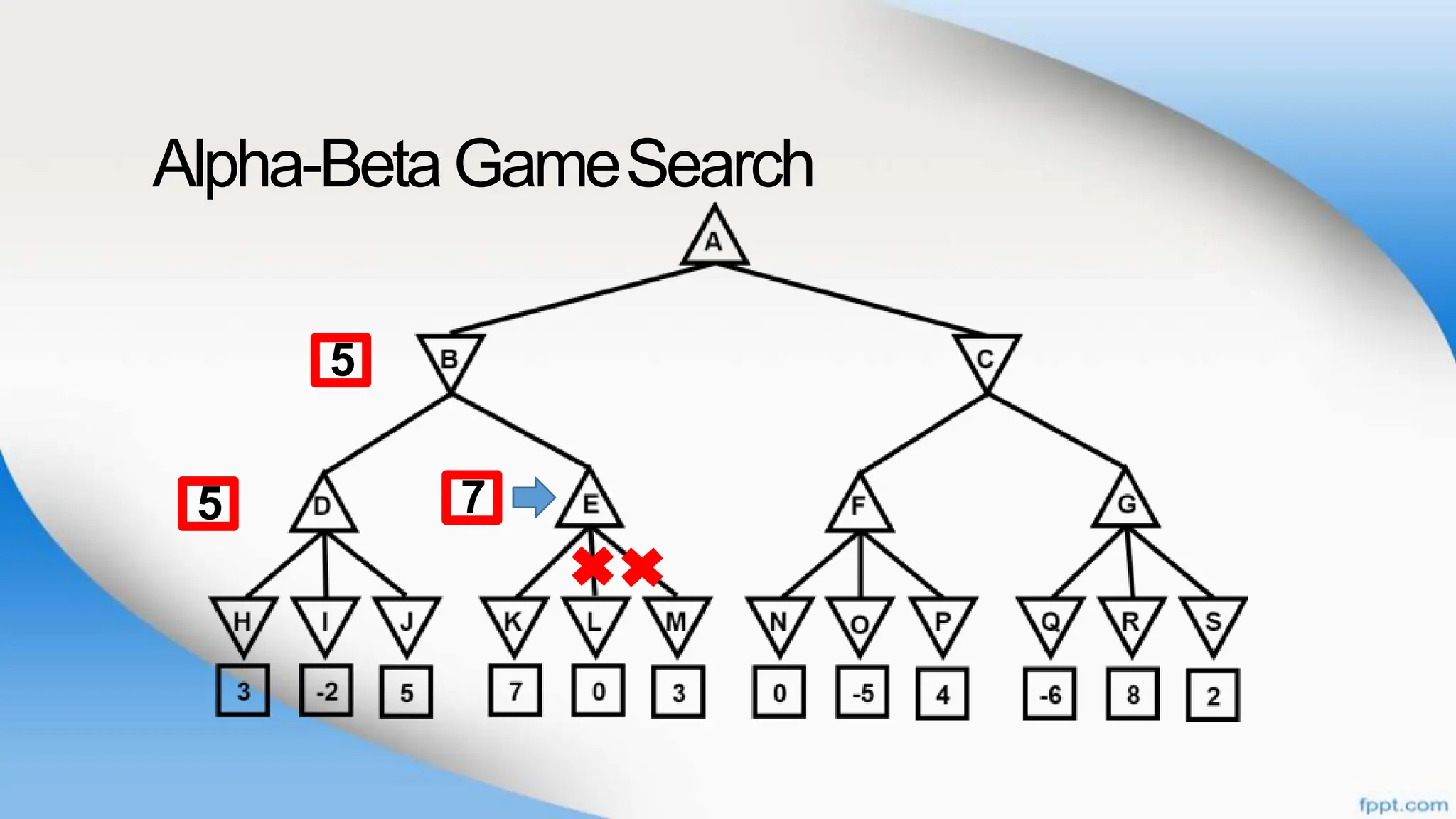
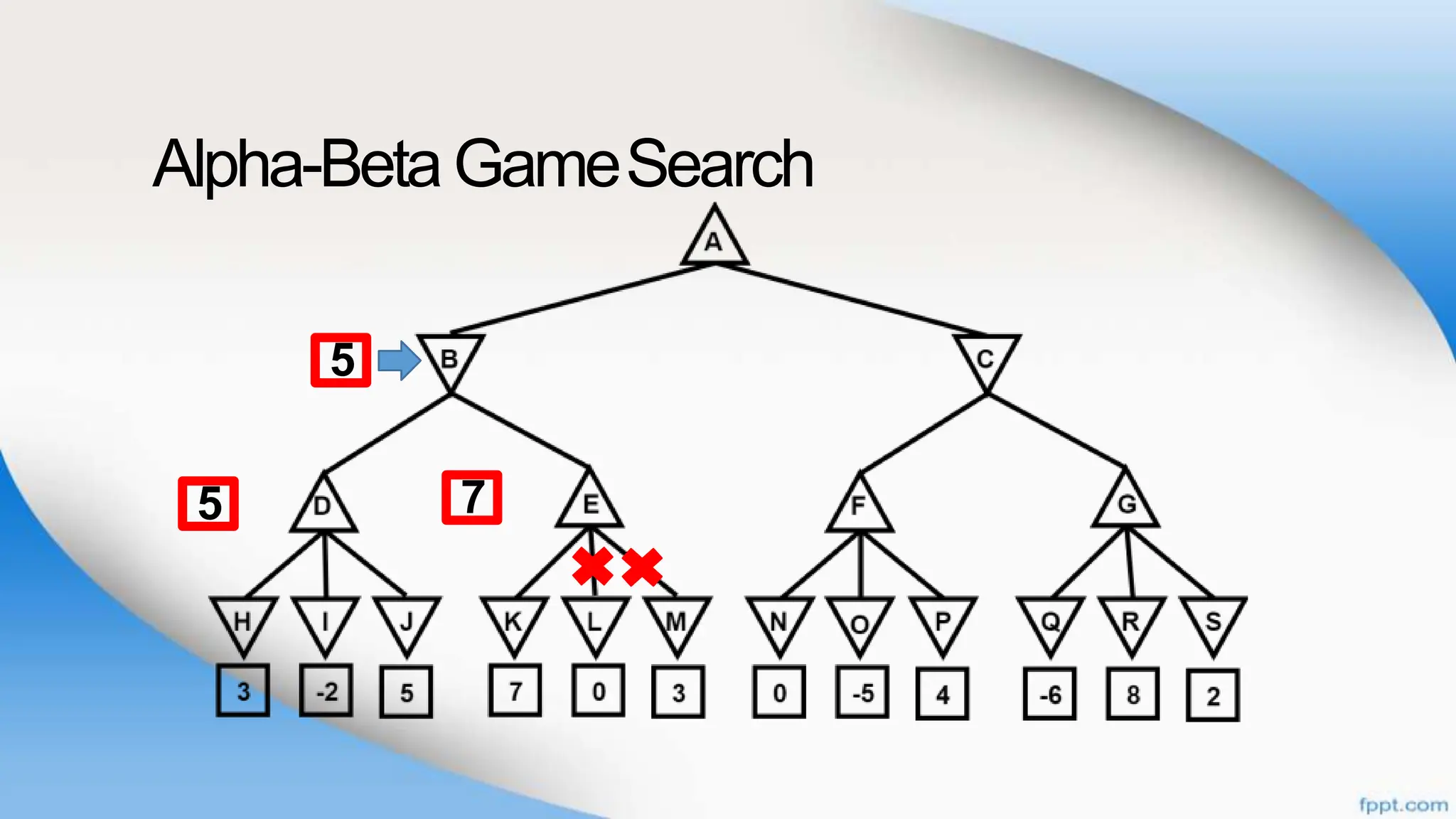
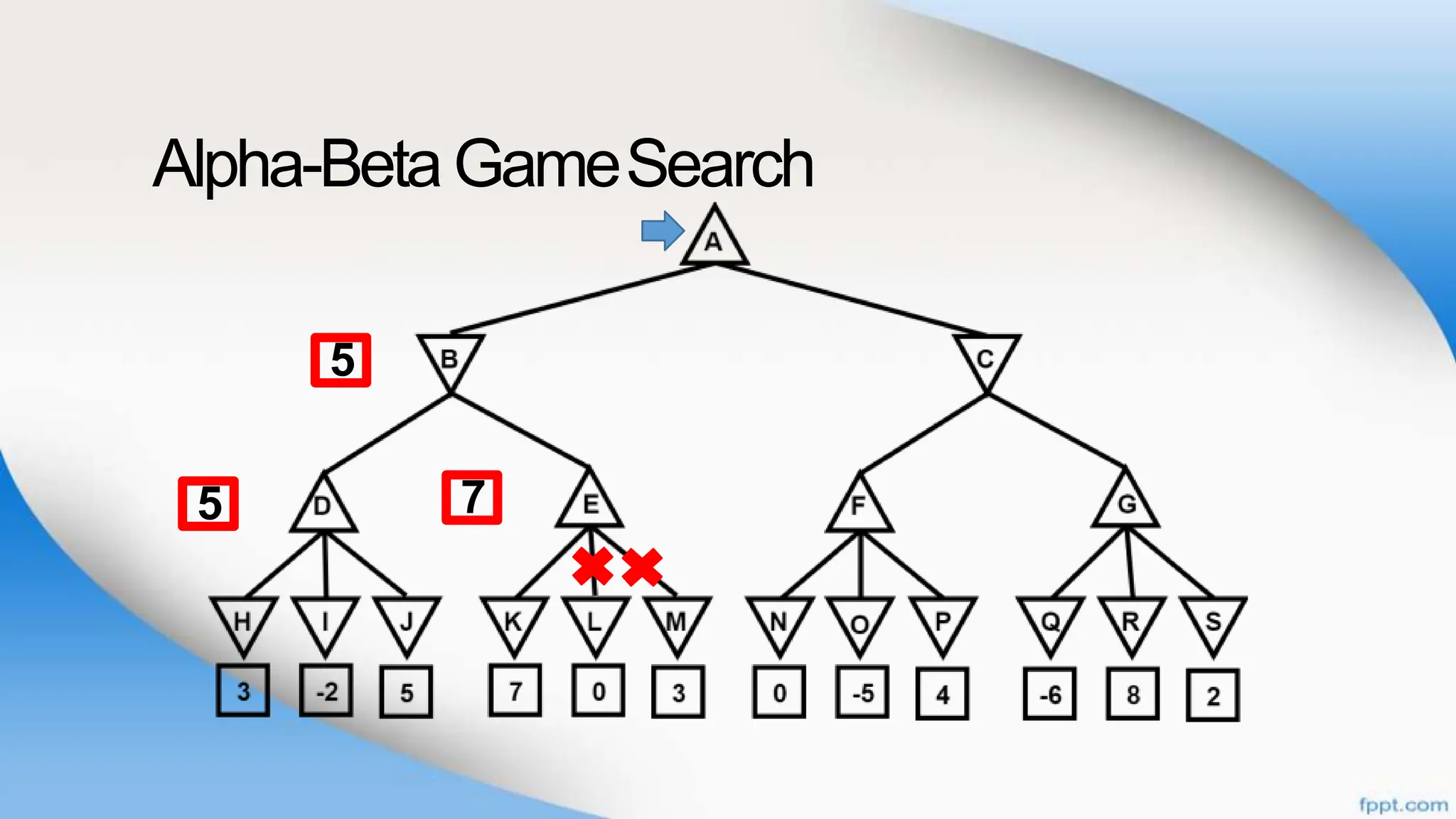
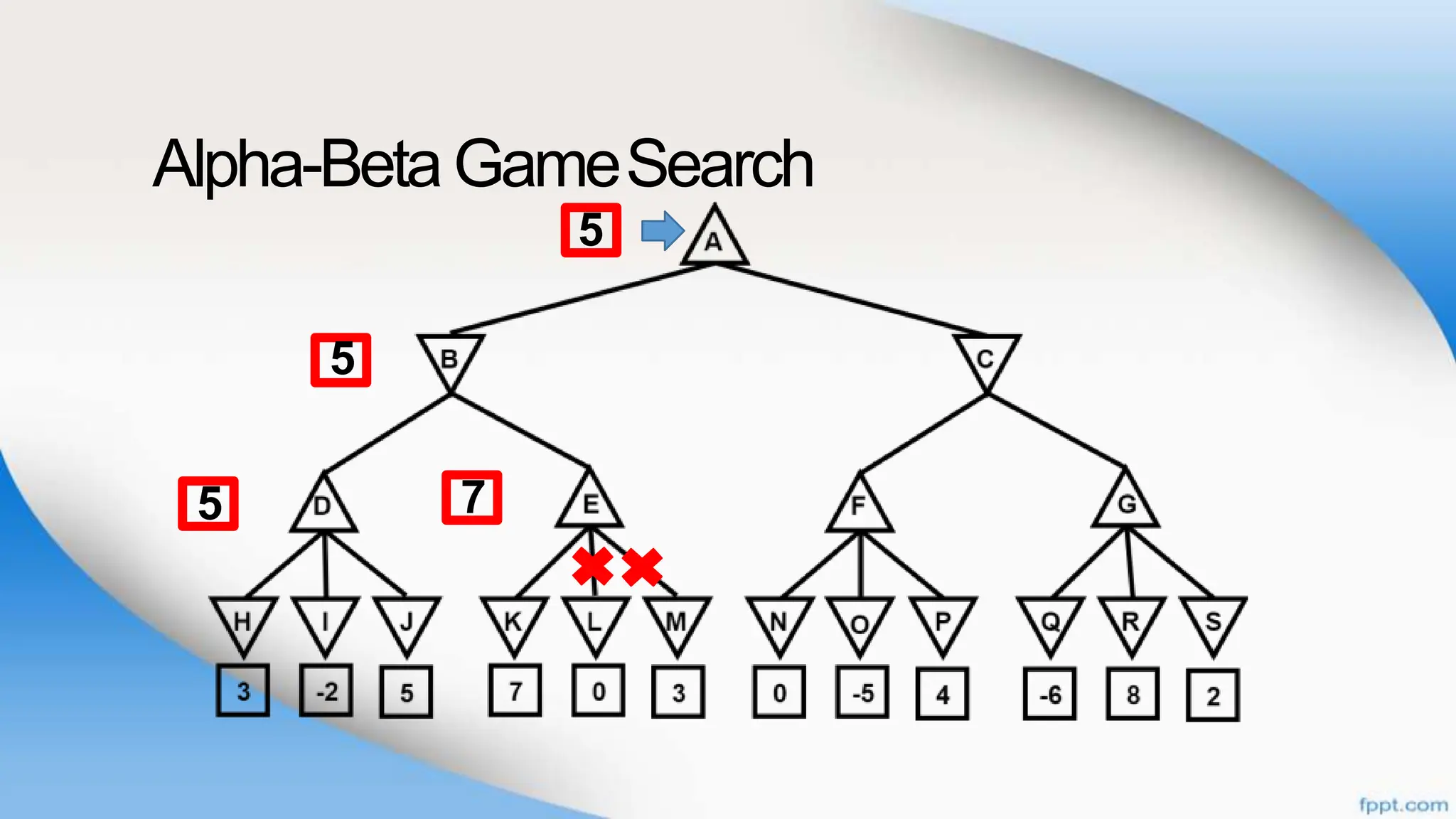
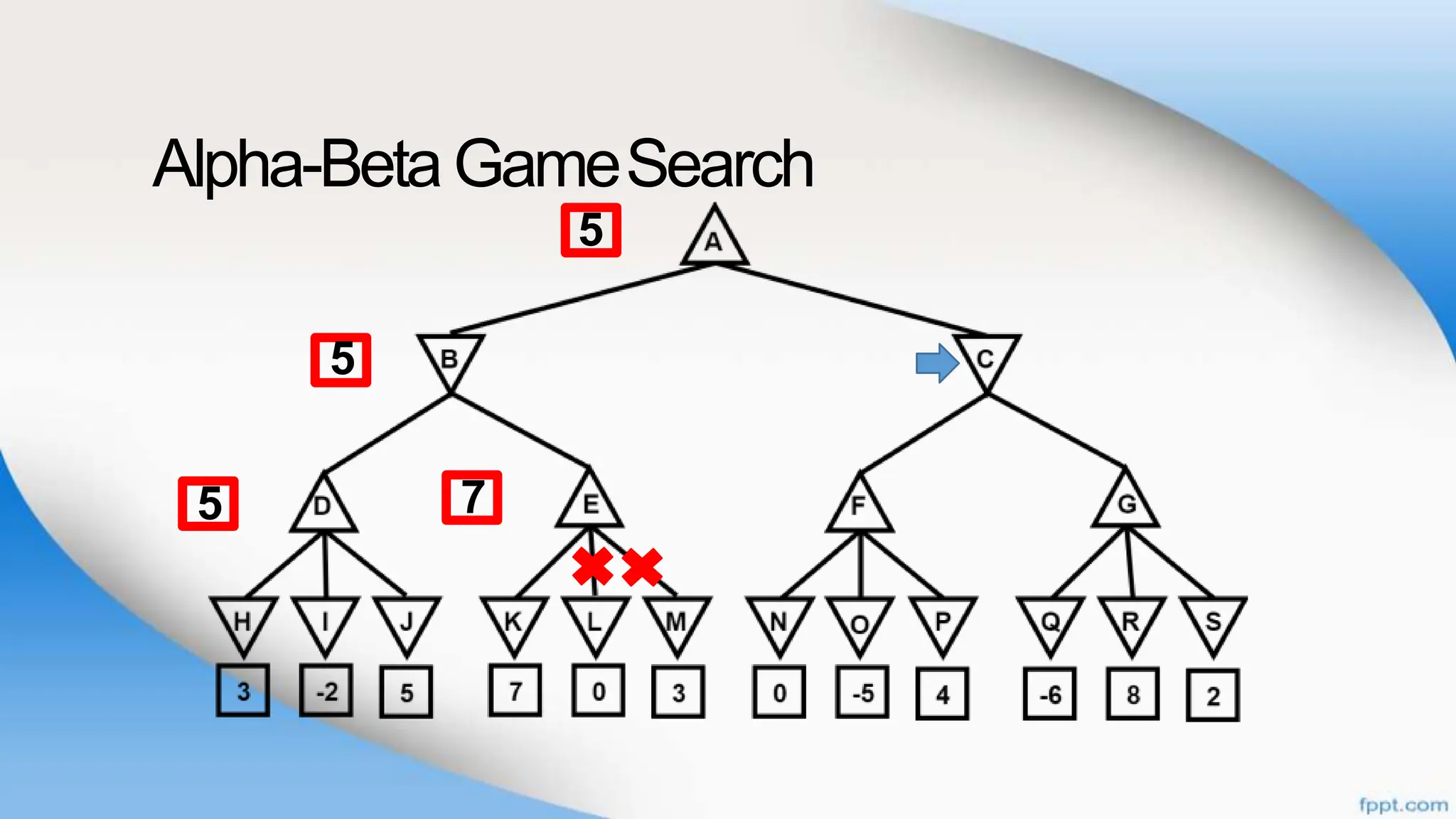
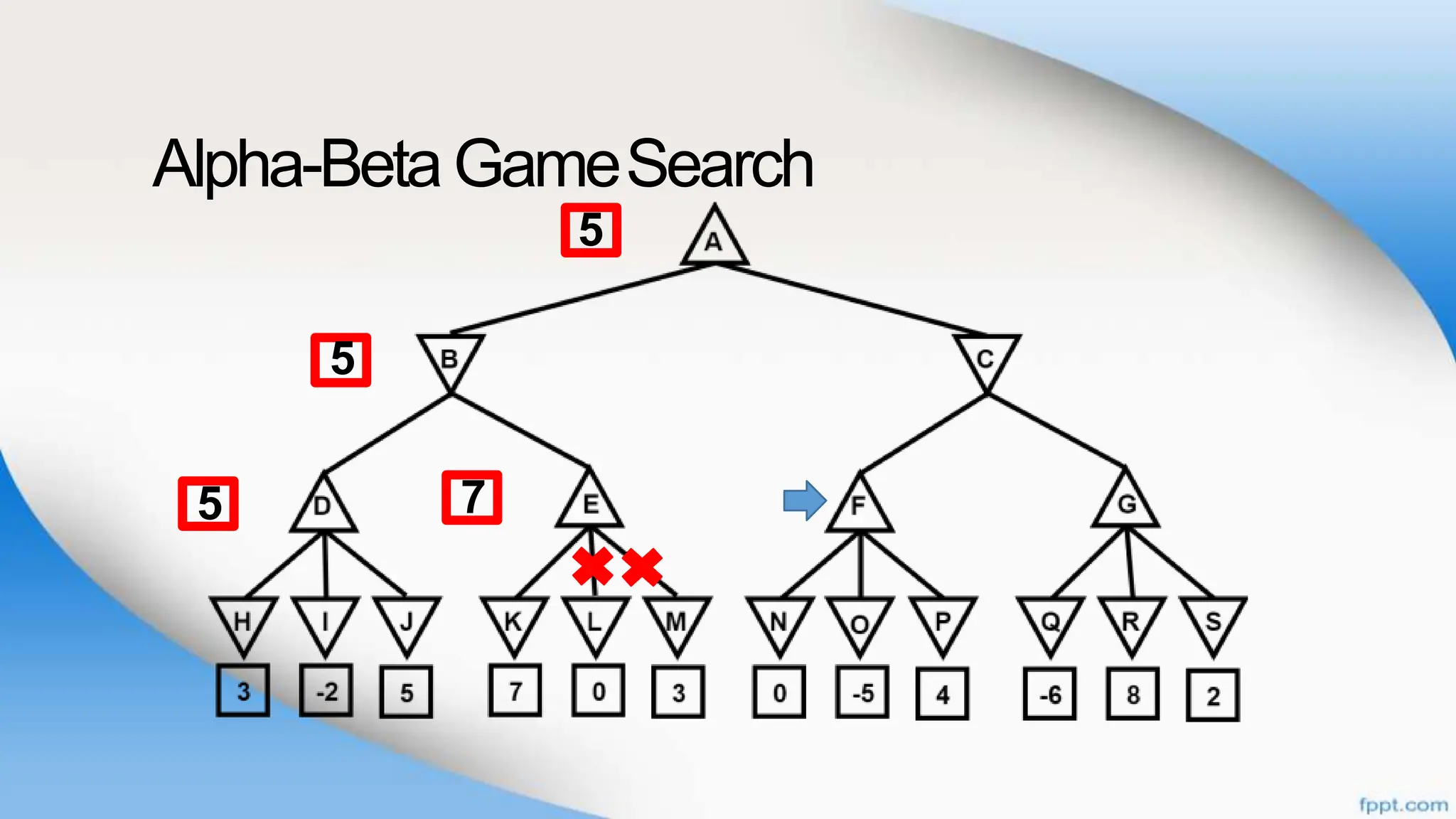
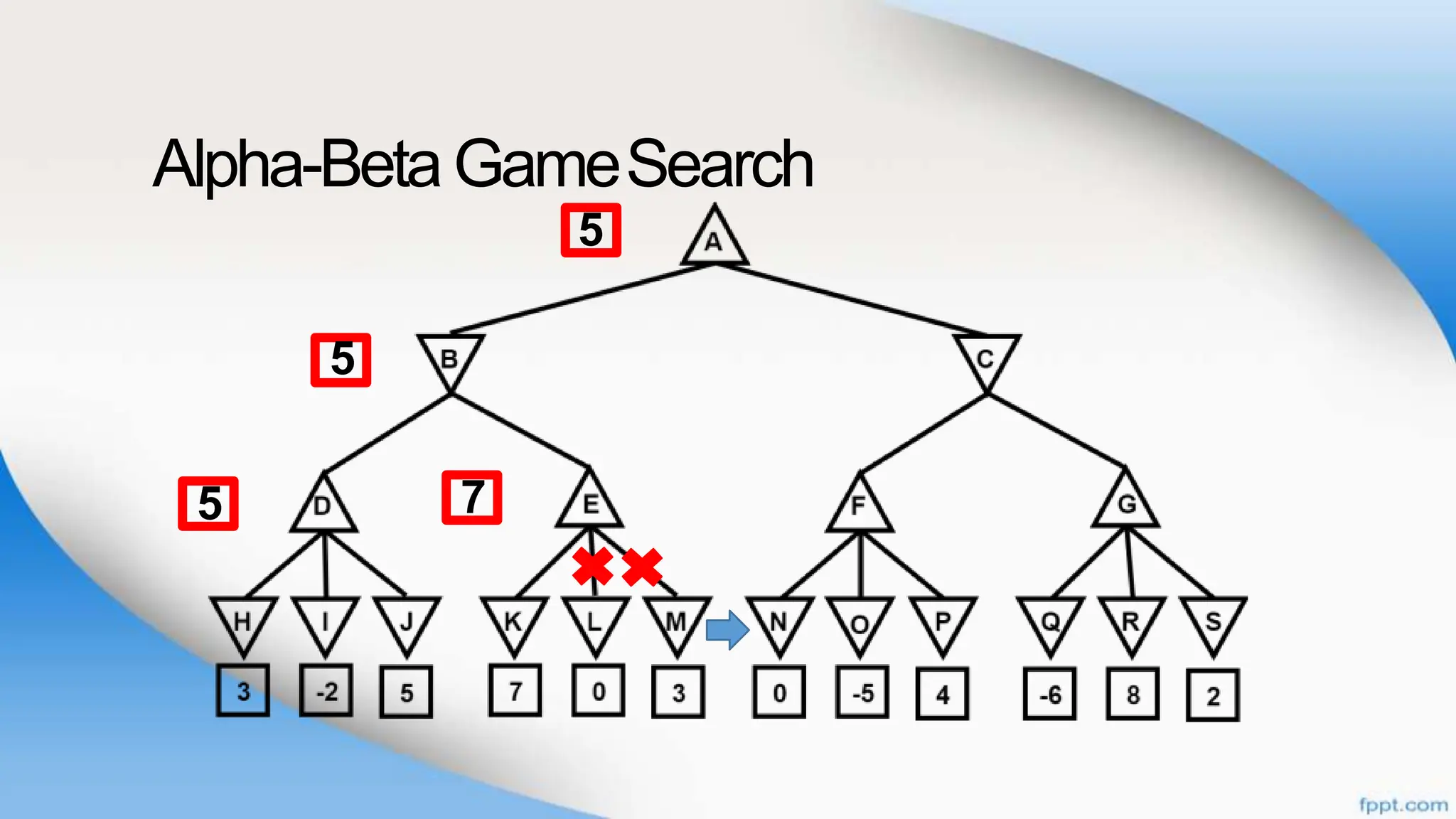
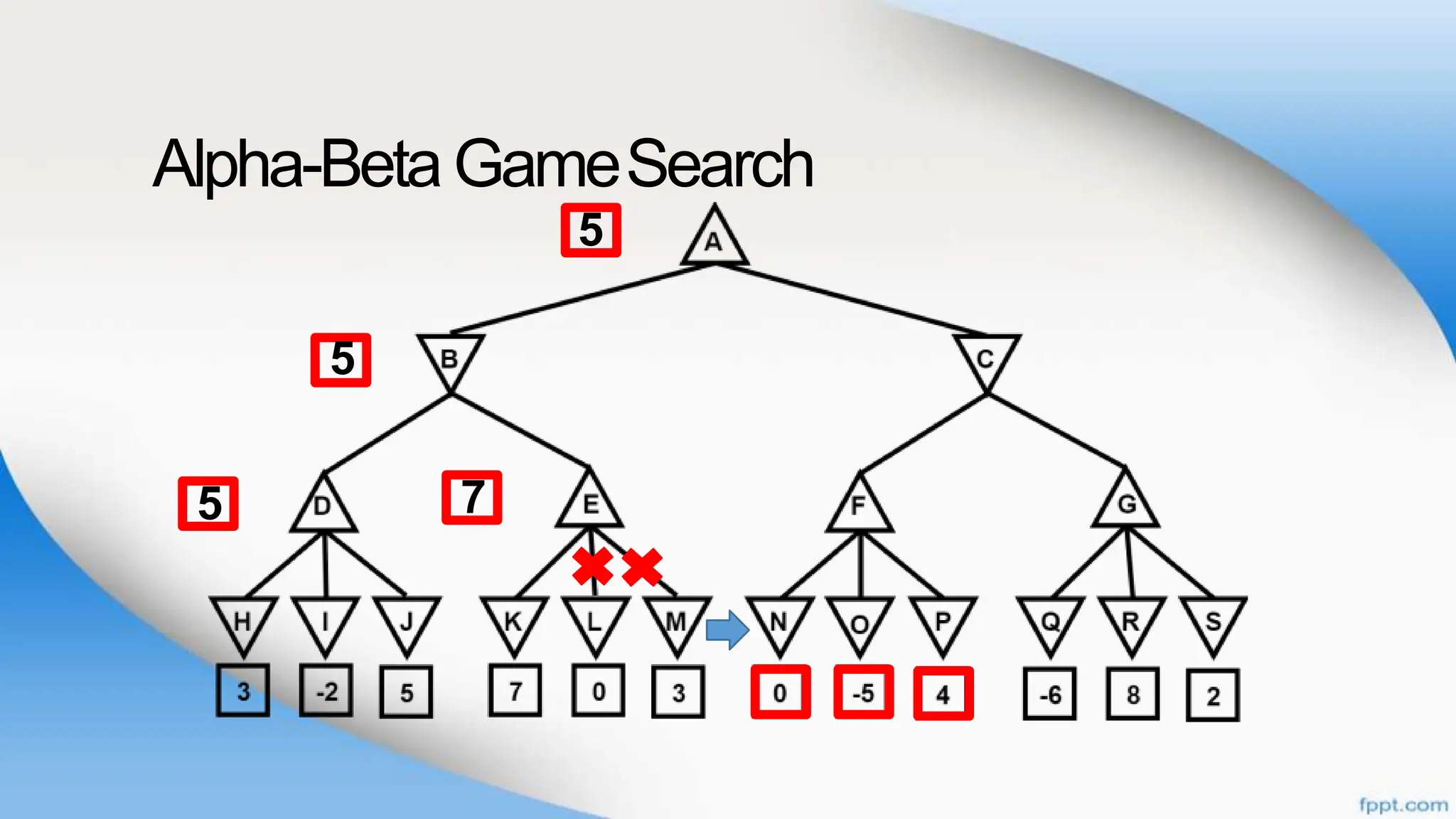
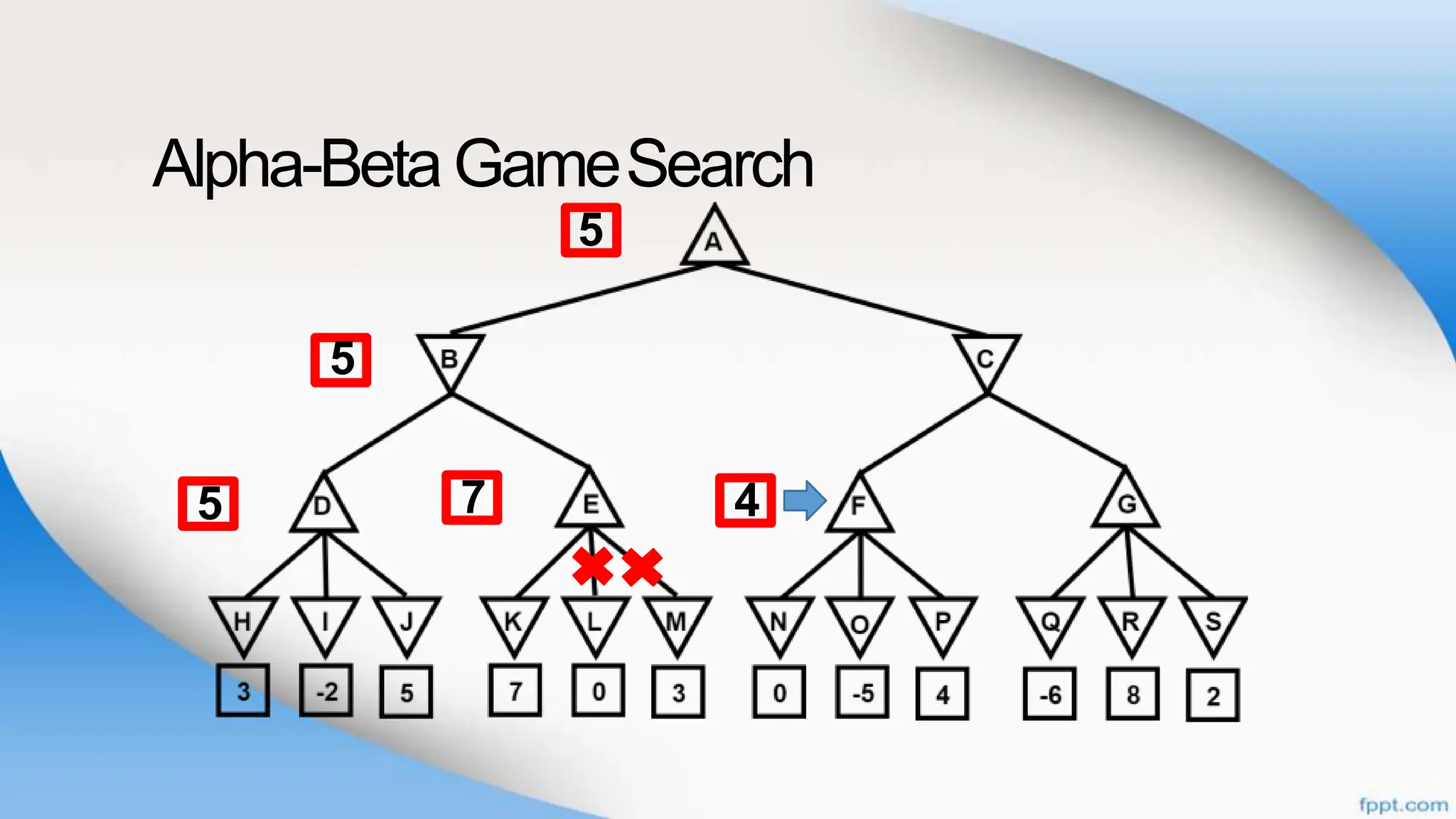
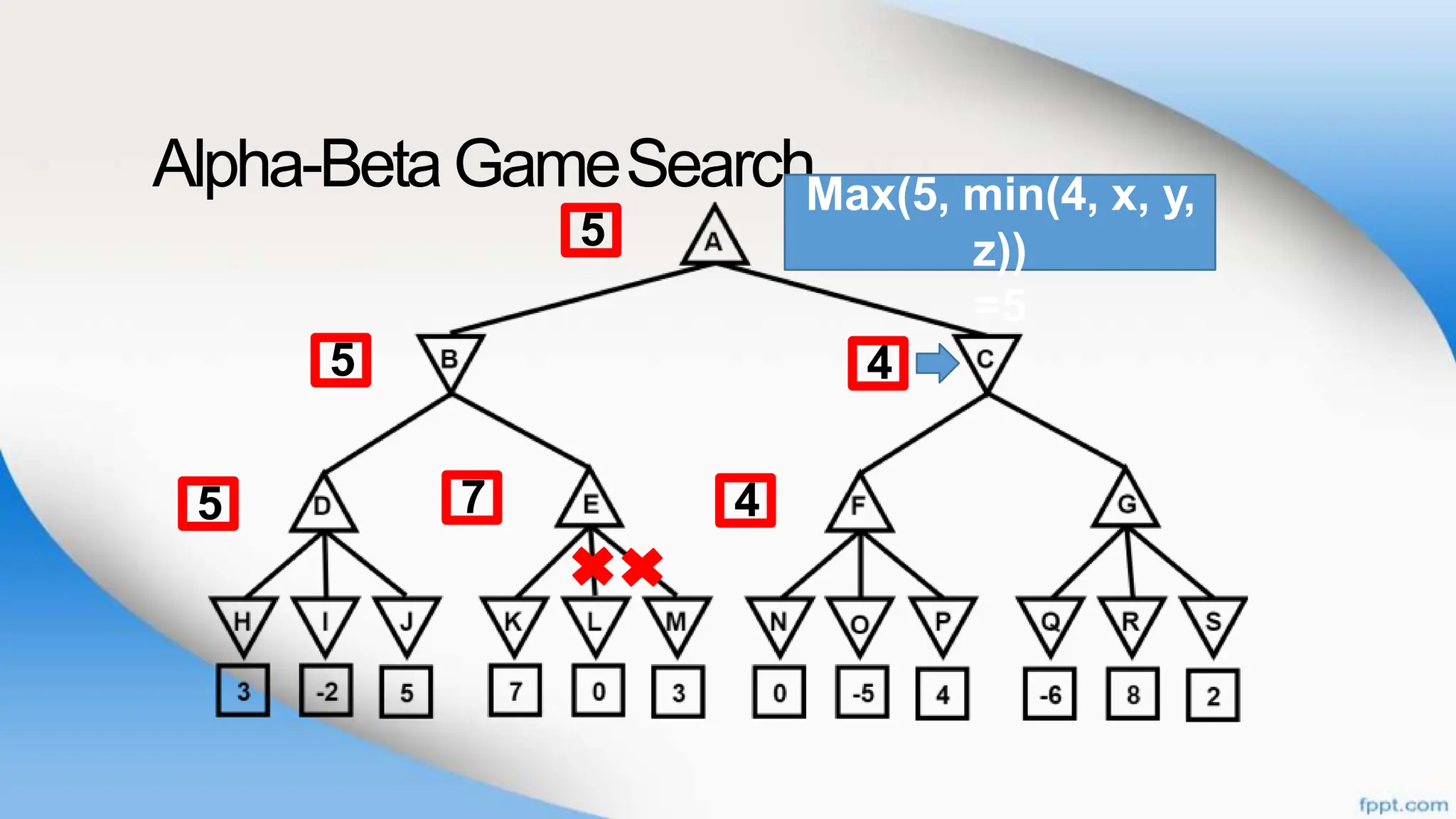
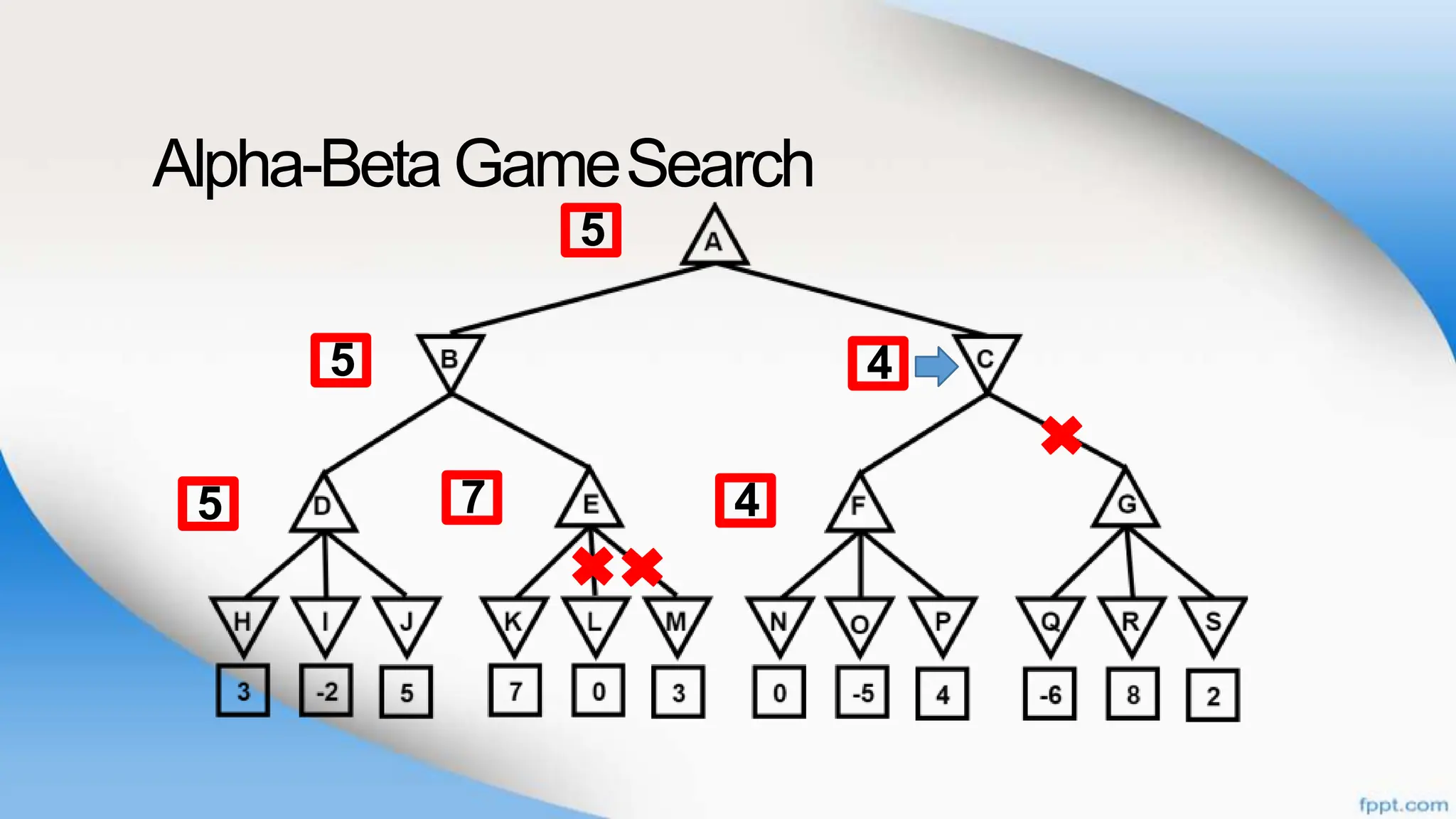
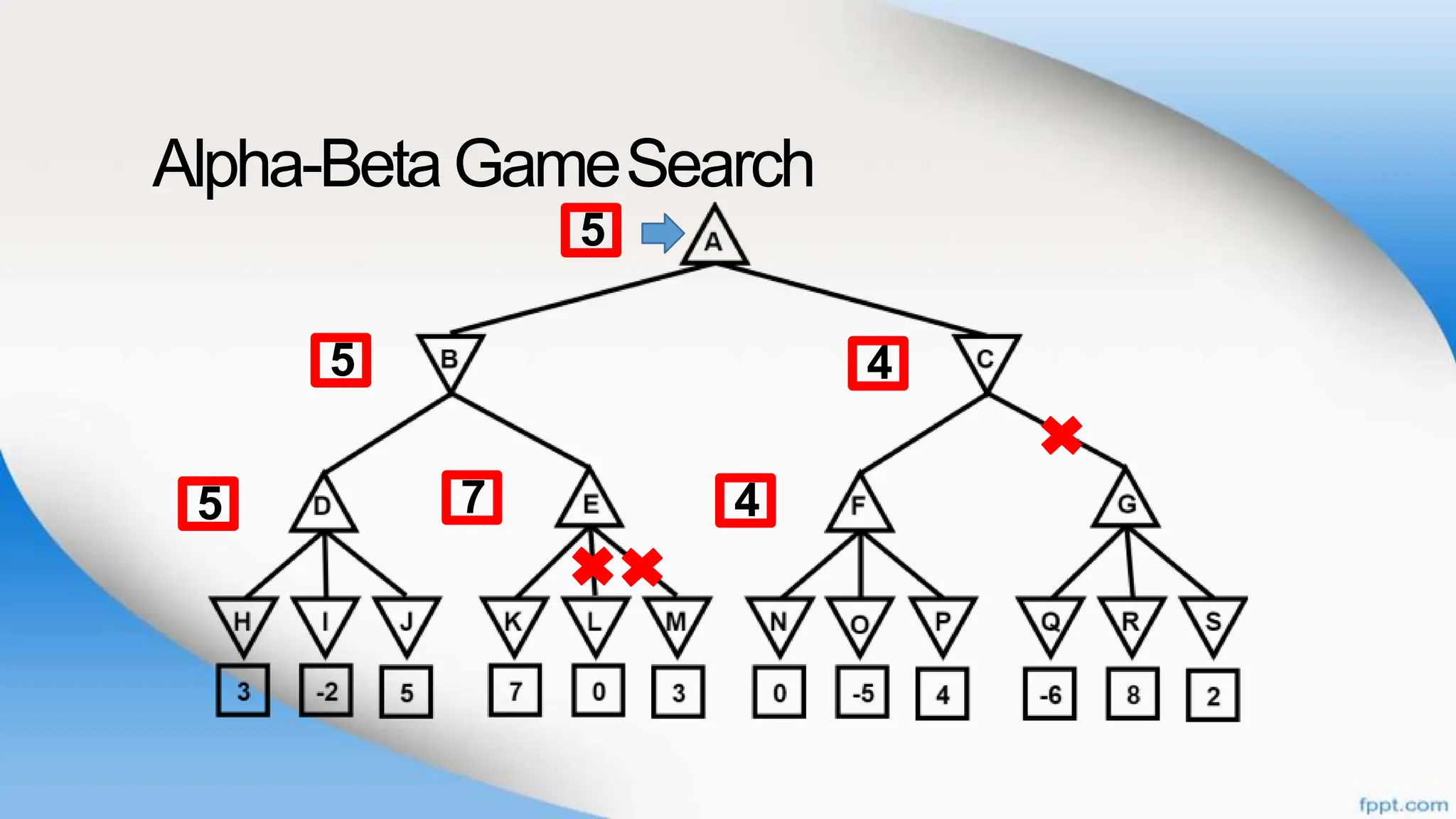
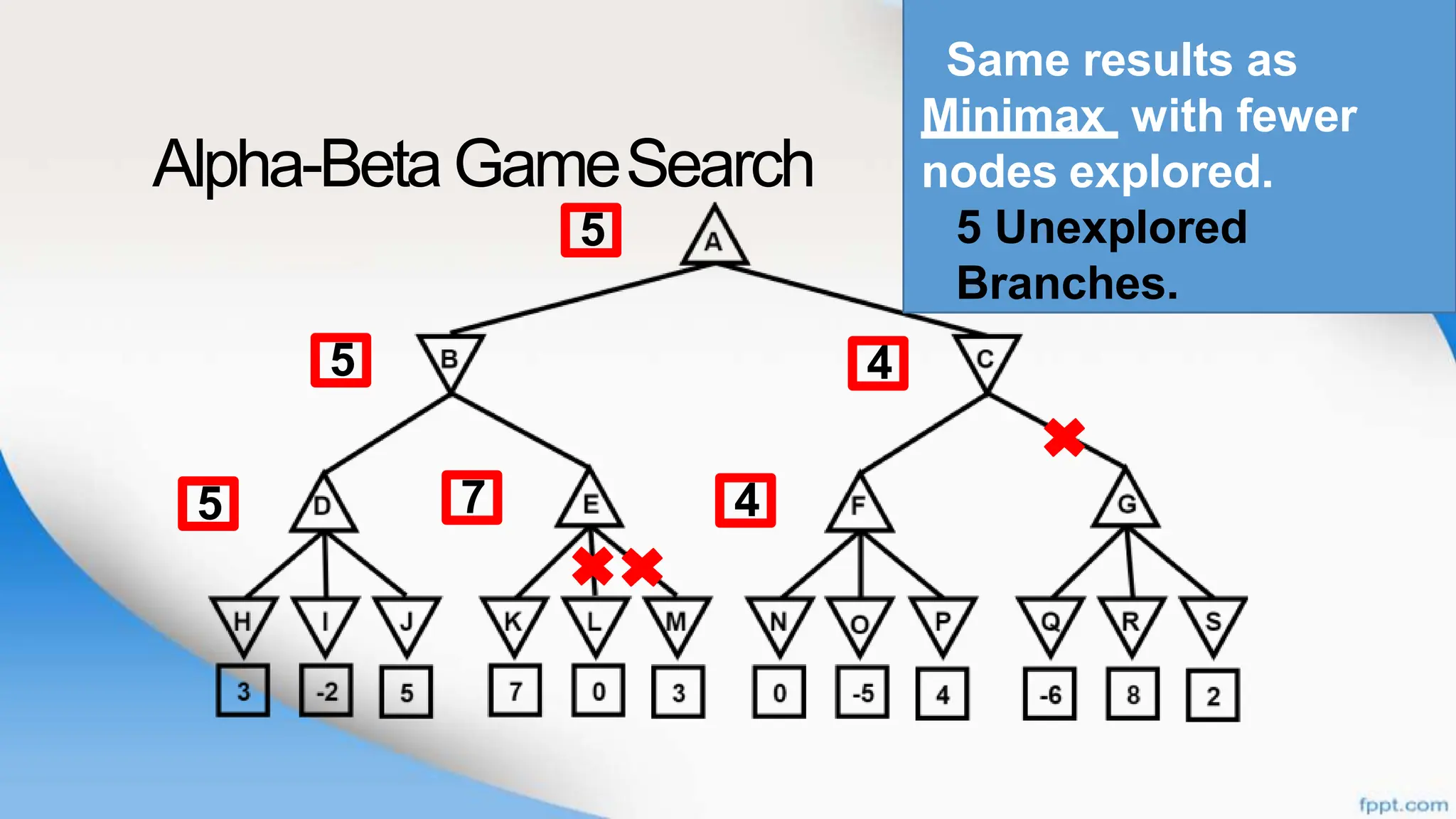
Alpha-beta pruning is a search algorithm that improves upon minimax by pruning branches that cannot possibly change the outcome. It evaluates nodes by assigning alpha and beta values, representing the best outcomes for max and min respectively. By comparing node values to alpha and beta, it can avoid exploring subtrees that won't affect the result. This allows alpha-beta pruning to evaluate games more efficiently than minimax by exploring fewer nodes.