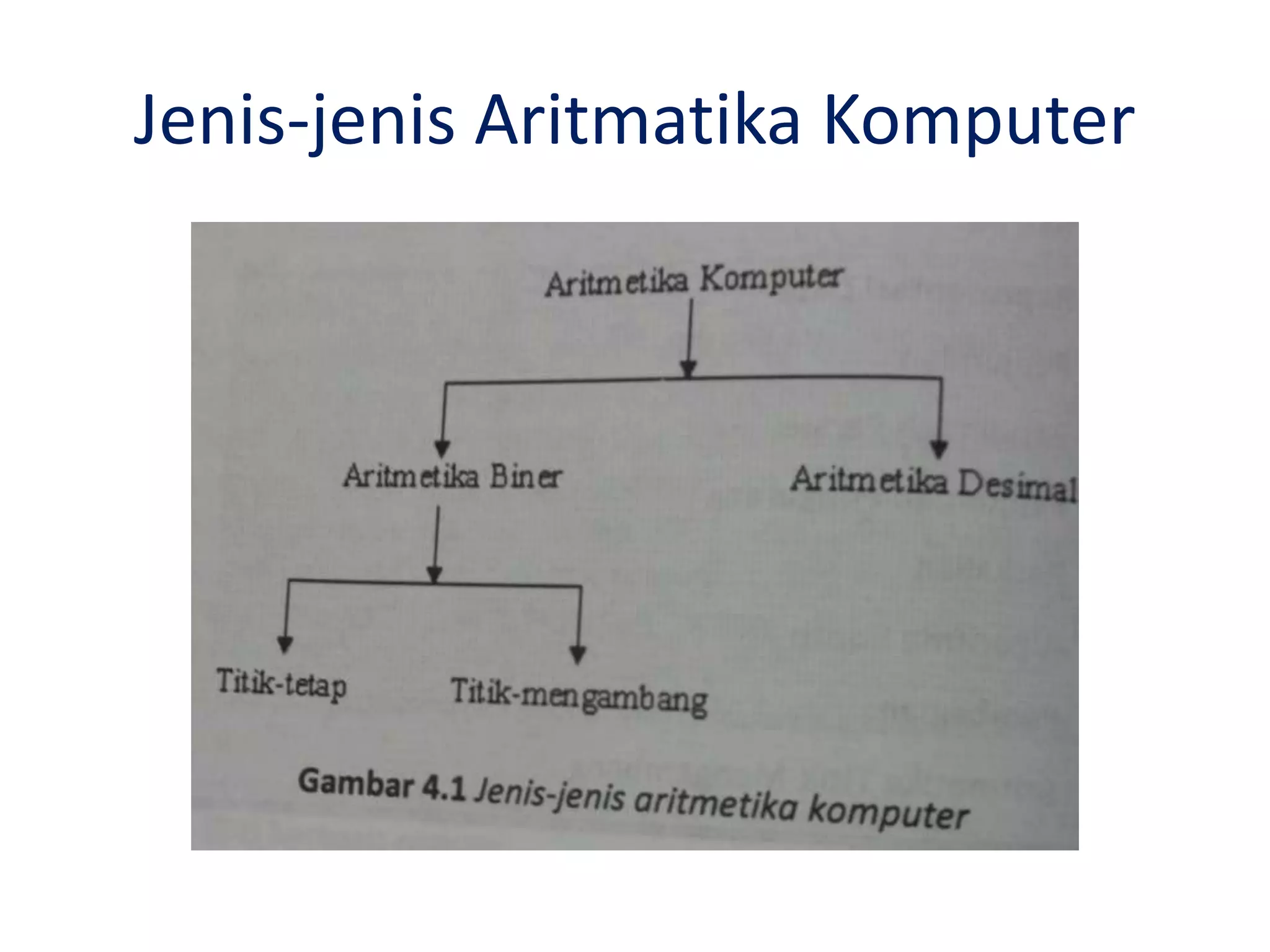
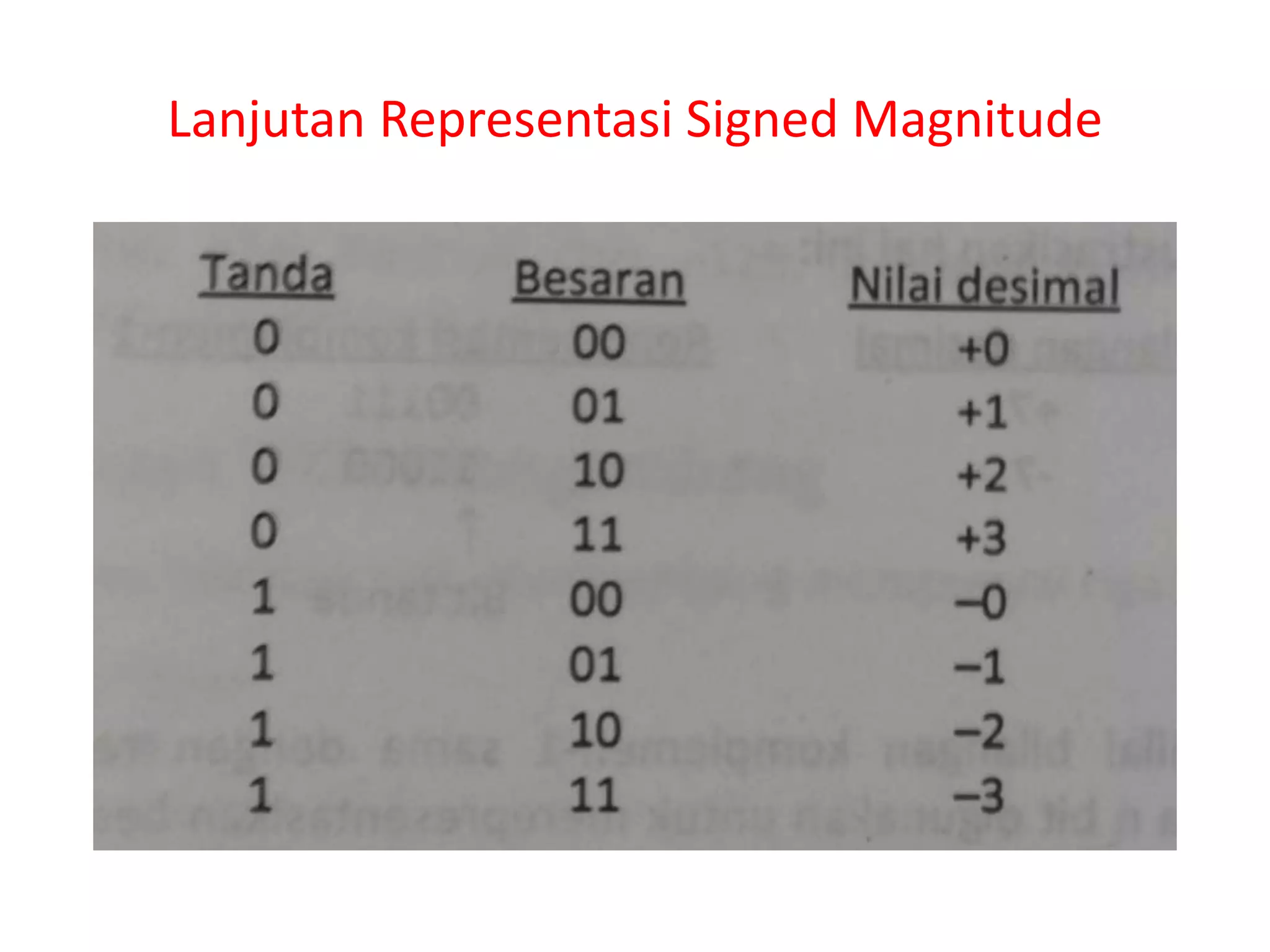
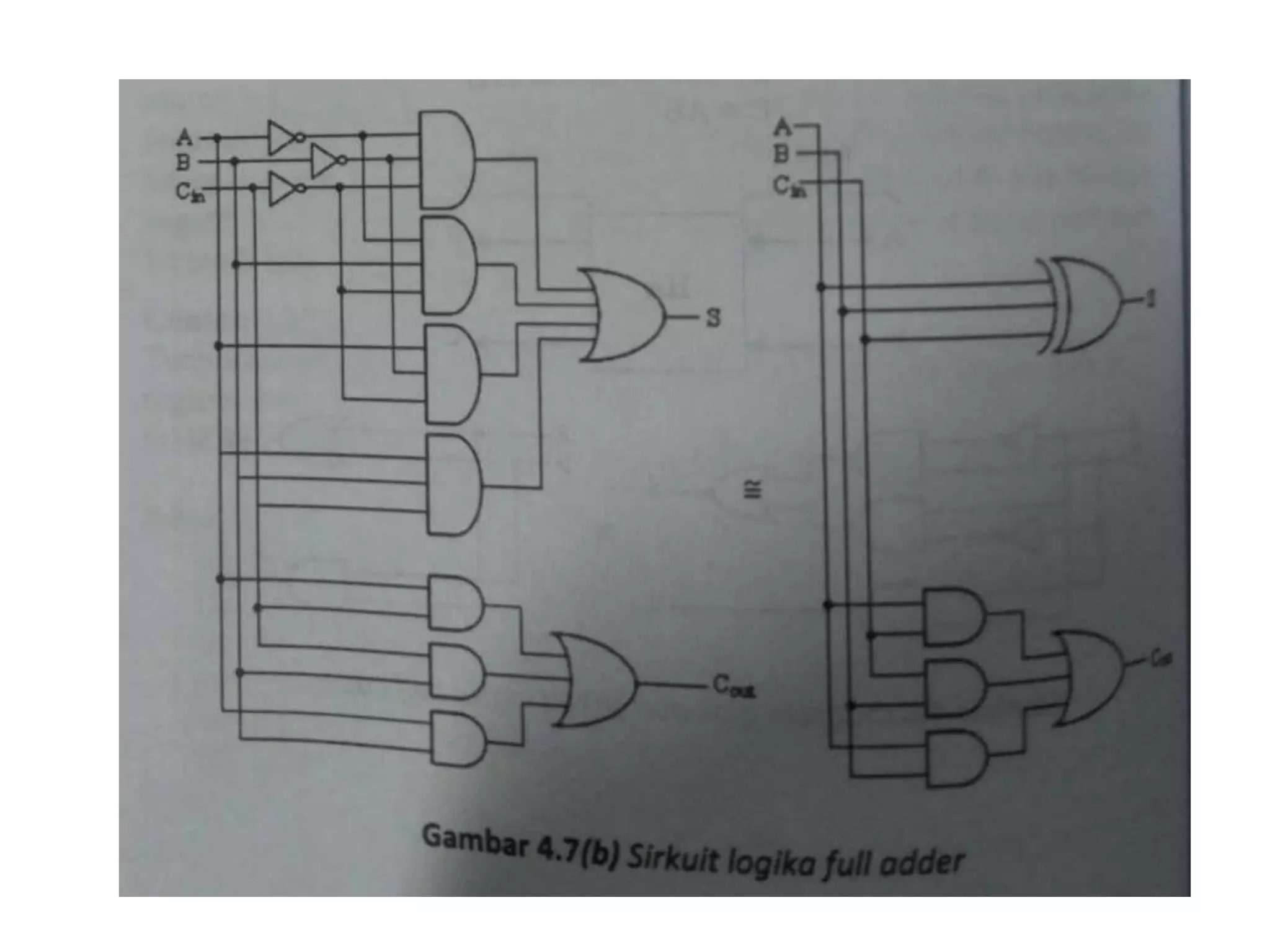
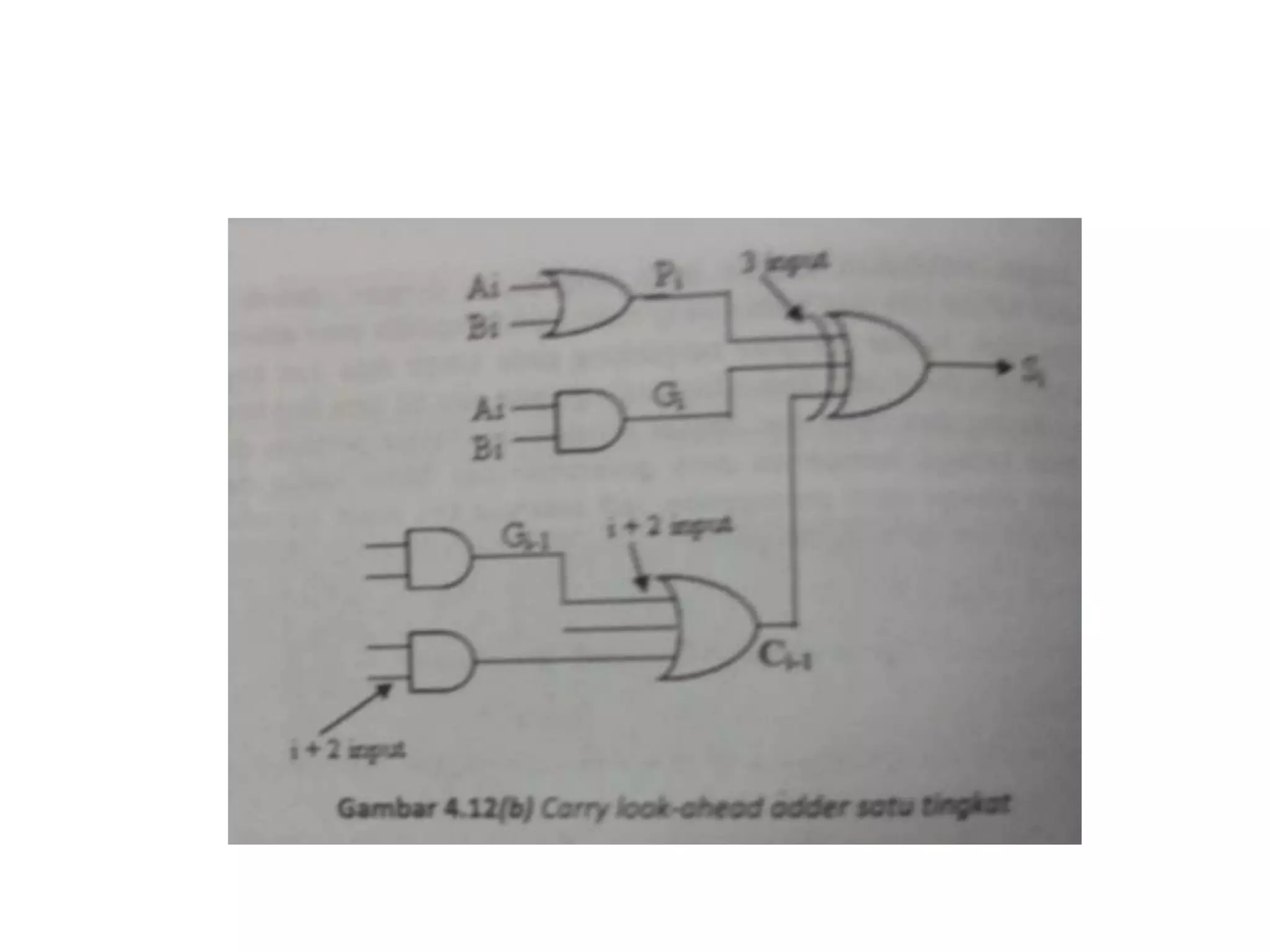
Dokumen ini menjelaskan komponen dasar aritmatika komputer, termasuk berbagai jenis gate dan flip-flop yang digunakan dalam sirkuit logika. Selain itu, dokumen membahas representasi data biner, baik titik tetap maupun titik mengambang, serta metode penjumlahan pada aritmetika bilangan. Ada juga penjelasan tentang adder, termasuk full adder dan berbagai jenis parallel adder dengan fokus pada cara mereka menghasilkan carry.

1. ARITMATIKA KOMPUTER
MUHAMMAD SIPAN

2. Jenis-jenis Aritmatika Komputer

3. Komponen-komponen Hardware
Komponen-komponen yang banyak digunakan dalam
aritmatika biner antara lain gate, latch, fli-flop, register,
counter, multiplexer, demultiplexer, decoder, encoder, dan
sebagainya.
GATE, sirkuit logika yang melakukan fungsi pada masukan-
masukan dan menghasilkan keluaran. Jenis gate berdasarkan
fungsi logikanya adalah: NOT, OR, AND, Exlusive OR, dan
sebagainya.
FLIP-FLOP, sebuah penyimpan biner satu bit ( memori satu bit)
yang menyimpan 0 dan 1. keluaran flip-flop dapat berubah
jika pemicuan sinyal clock.

4. Lanjutan Komponen-komponen Hardware
LATCH, merupakan flip-flop logika yang mengunci
status sinyal, sinyal gate mengontrol pembukaan
atau penutupan latch. latch digunakan untuk
mengambil suatu kondisi sebelum kondisi tersebut
hilang guna keperluan yang akan datang.
REGISTER, sekumpulan flip-flop dengan masukan
clock bersama, digunakan untuk penyimpanan atau
menahan sementara wprd di dalam pemrosesan (
operasi Logika).
SHIFT REGISTER, jenis register yang berfungsi untuk
melakukan pergeseran bit-bit didalam register,
pergeseran dilakukan kekiri atau ke kanan perbit
setiap masukan sinyal kontrol.

5. Lanjutan Komponen-komponen Hardware
COUNTER,berfungsi dalam pencacahan masukan pulsa clock,
pecacahan dapat dilakukan secara menaik atau menurun. Counter
digunakan dalam operasi aritmatika dan operasi-operasi kontrol.
MULTIPLEXER, untuk memilih salah satu dari beberapa input
kebagian output sesuai sinyal kontrol selector.
DEMULTIPLEXER, mengirim input ke salah satu dari beberapa
output sesuai sinyal selector. Disebut jg dengan data distributor,
demultiplexer berguna untuk konversi serial ke paralel.
DECODER, sebagai identifikasi atau penetapan pola pada n input
dengan mengaktifkan salah satu dari 2² output sesuaiangka input.
Digunakan untuk pengkodean intruksi, alamat dan perintah.
ENCODER, kebalikan decoder mempunyai sejumlah saluran input
dan hanya salah satu yang di aktifkan pada satu waktu dan
menghasilkan kode output sebanyak n-bit bergantung pada input
yang aktif.

6. Representasi Data
• Data Karakter
Kumpulan bit untuk mempresentasikan sebuah
karakter yang mungkin berupa sebuah digit, sebuah
alphabet atau simbol khusus dan sebagainya.
• Data biner
Data biner dapat dipresentasikan sebagai
bilangan tetap atau bilangan titik mengambang. Pada
representasi titik tetap, posisi dari titik biner adalah
sudah pasti tetap dalam satu tempat. Pada
representasi titik mengambang posisi biner dapat
berada di mana saja. Bilangan titik tetap dikenal
dengan bil. Integer atau bilangan bulat, dan bil. Titik
mengambang di sebut bil. Pecahan atau desimal.

7. Keuntungan bilangan titik mengabang dibandingkan
bilangan titik tetap
Dengan jumlah bit data yang diberikan, nilai
maksimum dan minimum yang dapat di
representasikan dalam representasi bilangan titik
mengambang lebih tinggi daripada bil. Titik tetap.
Bilangan ini berguna untuk keperluan bilangan yang
sangat besar atau bilangan yang sangat kecil.
Representasi bil. Titik mengambang lebih akurat
dalam operasi aritmatika.

8. Aritmatika Bilangan Titik-Tetap
Pada bilangan titik tetap, posisi biner adalah tetap,
tetapi tdk ditunjukkan secara eksplisit pada
komputer.
Jenis-jenis Representasi Bilangan Titik-tetap.
Bilangan titik tetap dapat berupa bilangan
bertanda atau bilangan tak bertanda. Ada tiga jenis
representasi bilangan titik tetap :
1. representasi Signed magnitude
2. Representasi komplemen-1
3. Representasi komplemen-2

9. Representasi Signed Magnitude
Biasa juga disebut representasi benar karena
pola bit yang digunakan tidak ada perubahan
sepanjang bit tandanya. Contoh ilustrasi berikut
adalah bentuk signed magnitude( posisi bit tanda
ditunjukkan oleh panah).

10. Jika kita memiliki 1 bit tanda dan 2 bit untuk
besaran ( magnitude) maka rentang bilangan yang
dapat di presentasikan oleh sistem 3 bit ini dalam
bentuk signed magnitude adalah dari -3 sampai +3
seperti ditunjukkan berikut :
Jika n bit digunakan untuk merepresentasikan
besaran, maka rentang yang dapat di representasikan
oleh signed magnitude adalah -(2²⁺ᴵ -1) hingga +(2² ̄ᴵ-
1)

11. Lanjutan Representasi Signed Magnitude

12. Representasi Komplemen-1
Komplemen-1 sebuah ilangan diperoleh dengan
cara melakukan pembalikan setiap bit, semua bit 1
diubah menjadi 0 dan semua bit 0 diubah menjadi 1.
contoh berikut mengilustrasikan pembentukan
komplemen-1 :

13. Representasi Komplemen-2
Komplemen-2 suatu bilangan diperoleh dengan
menambahkan 1 pada komplemen-1 bilangan
tersebut. Contoh berikut mengilustrasikan
pembentukan komplemen-2 :

14. Bilangan Titik Mengambang
Representase bilangan titik mengambang
mempunyai tiga bagian :
1. Mantissa
2. Basis
3. Eksponen
Mantisa dan eksponen di representasikan secara
ekplisit dalam komputer, tetapi basisnya adalah
yang digunakan oleh komputer tersebut. Umumnya
komputer mengikuti basis 2. pada umumnya
sebuah bilangan f direpresentasikan sebagai f = m x
rᵉ.
Contoh :

16. Aritmatika bilangan titik tetap
Penjumlahan Integer
Dua jenis penjumlahan yang dibutuhkan
didalam ALU :
1. Penjumlahan bilangan tak bertanda.
2. Penjumlahan bilangan bertanda.
Untuk membangun sirkuit aritmatika
komputer maka dibutuhkan sirkuit adder (
penjumlah) dasar yaitu hal adder dan ful
adder.

17. Half adder
Sebuah penjumlahan yang melakukan
penjumlahan dua bilangan biner 1 bit.
Contoh :

18. Full adder
• Penjumlah yang melakukan penjumlahan tiga
bilangan biner 1 bit, yaitu dengan masukan A dan B,
serta masukan ketiga berasal dari carry in (Cin).
Dibawah ini ini di tunjukkan blok full adder. SUM (S)
dan carry out (Cout):

20. Serial Adder
• Hanya mempunyai sebuah penjumlah bit
tunggal.serial adder digunakan untuk penjumlahan
dua bilangan secara sekuensial bit demi bit yang
dimulai dari LSB.

21. Parallel adder
Sebuah penjumlahan yang mempunyai beberapa
full adder terpisah yang dikaskadekan menjadi satu
grup. Parrallel adder melakukan penjumlahan dari
multi fulladder secara simultan. Mekanisme
penjumlahan internal berbeda pada setiap jenis
parallel adder. Pada dasarnya ada dua jenis parallel
adder :
1. Ripple carry adder
2. Carry look-ahead adder
Perbedaan keduanya pada cara carry bit
dibangkitkan

22. Ripple carry adder
Preosesnya adalah sebagai berikut : ada n-bit full
adder yang dihubungkan dengan cara kaskade.
Setiap carry out dari full adder menjadi carry in bagi
full adder bit berikutnya. Setiap tingkat melakukan
penjumlahan untuk salah satu bit dari dua bilangan
dan carry dari posisi bit sebelumnya. Setiap tingkat
adder menghasilkan satu bit hasil-jumlah dan satu
bit carry.

23. Kaskade ripple carry adder
Ditunjukkan kontruksi adder 2n-bit menggunakan dua
adder n-bit dari jenis ripple carry adder. Kedua modul
melakukan penjumlahan secara simultan dan kemudian
mengizinkan perambatan carry dari satu modul ke modul
berikutnya.

25. Carry look Ahead adder
Penjumlahan kecepatan tinggi yang mengikuti suatu
strategi khusus untuk membangkitkan carry yang cepat pada
setiap tingkat tanpa menunggu carry dari tingkat
sebelumnya.dia menggunakan determinasi/penentuan dini
carry in ke suatu tingkat tanpa menggunakan carry out dari
tingkat sebelumnya.
Contoh :
C₀=A₀B₀; C₁ = A ₁ C ₀+A ₁ B ₁ +B ₁ C ₀=A ₁ B ₁ +C₀(A ₁ +B ₁ )
C₀ adalah carry out dari LSB yaitu adder tingkat 0
C ₁ adalah carry out tingkat 1.
Jika adder dengan tingkat i, maka carry out dari tingkat ini
dinyatakan dengan
Cᵢ = AᵢBᵢ + (Aᵢ+Bᵢ) Cᵢ- ₁