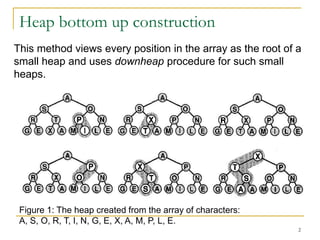
The document describes the heap bottom-up construction method for building a heap from an array in linear time O(M) where M is the number of elements. It works by viewing each element in the array as the root of a small heap and using a downheap procedure to satisfy the heap property from the bottom up. Starting from the lowest levels with single element heaps, it calls downheap on progressively larger heaps until the full array is a valid max heap.

1. Appendix A: Heap Bottomup Construction
Course: Algorithm Analysis and Design
1

2. Heap bottom up construction
This method views every position in the array as the root of a
small heap and uses downheap procedure for such small
heaps.
Figure 1: The heap created from the array of characters:
A, S, O, R, T, I, N, G, E, X, A, M, P, L, E.
2

3. Heap bottom-up construction procedure
procedure build_heap;
begin
for k:= M div 2 downto 1 do
downheap(k);
end
M: the number of elements in the heap.
The keys in a[ (M div 2)+1 .. M] each form heaps of one
element, so they satisfy the heap condition and don’t
need to be checked.
3

4. Property: Bottom-up heap construction is lineartime.
For example: To build a heap of 127 elements, the
method calls downheap on
- 64 heaps of size 1
- 32 heaps of size 3
- 16 heaps of size 7
- 8 heaps of size 15
- 4 heaps of size 31
- 2 heaps of size 63
- 1 heaps of size 127
So the method needs 64.0 + 32.1 + 16.2 + 8.3 + 4.4 +
2.5 + 1.6 = 120 “promotions”.
0.26 + 1.25 + 2.24 + 3.23 + 4.22 + 5.21 + 6.20

4

5. 0.26 + 1.25 + 2.24 + 3.23 + 4.22 + 5.21 + 6.20
(M= 127 = 27 -1) m = 7
For M = 2m, an upper bound on the number of comparisions is
(1-1)2m-1 + (2-1)2m-2 + (3 -1)2m-3+… + (k-1)2m-k + … (m-1-1)2m-(m-1)
+ (m -1)2m-m.
= 1.2m-2 + 2.2m-3 +3.2m-4+ 4.2m-5 +…+ (k-1)2m-k + …
(m-2)21 + (m -1)20
= (2m-2 + 2m-3 + …+ 20) + (2m-3 + …+ 20) + (2m-4 + …+ 20) …+(22 + 21
+ 20) + (21 + 20) + 1
= (2m-1 -1)+ (2m-2 -1) + … (23-1) + (22-1) +(21-1)
= (2m-1 + 2m-2 + … 22 + 21)– m +1
= (2m-1 + 2m-2 + … 22 + 21+1) – m
= (2m -1) – m < M
So the complexity of heap bottom-up building is O(M).
5