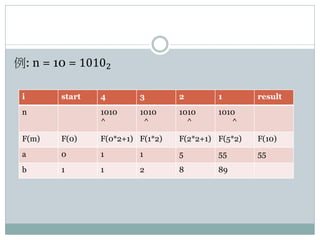
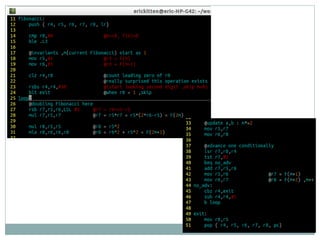
This document describes an algorithm for calculating Fibonacci numbers in O(log n) time using matrix multiplication and fast doubling. It involves representing the Fibonacci sequence as a matrix and using the properties that F(2k) = F(k)[2F(k+1) - F(k)] and F(2k+1) = F(k+1)^2 + F(k)^2. Pseudocode and an ARM assembly implementation are provided. Examples are given to calculate F(10) using this fast doubling approach.

1. 吳 哲 綱
2015.3.17
Fast doubling Fibonacci : arm
assembly實作

2.  複雜度𝑂(log 𝑛)
 不需要floating point運算

3. 公式
 矩陣表示式
1 1
1 0
𝑛
=
𝐹(𝑛 + 1) 𝐹(𝑛)
𝐹 𝑛 𝐹(𝑛 − 1)
 Fast doubling
𝐹 2𝑘 = 𝐹(𝑘)[2𝐹(𝑘 + 1) − 𝐹(𝑘)]
𝐹(2𝑘 + 1) = 𝐹(𝑘 + 1)2
+ 𝐹(𝑘)2

4. 證明-矩陣表示式
 以數學歸納法證明：
1 𝑛 = 1;
1 1
1 0
1
=
𝐹(2) 𝐹(1)
𝐹(1) 𝐹(0)
2 設
1 1
1 0
𝑛
=
𝐹(𝑛 + 1) 𝐹(𝑛)
𝐹 𝑛 𝐹(𝑛 − 1)
成立
⇒
1 1
1 0
𝑛+1
=
𝐹(𝑛 + 1) 𝐹(𝑛)
𝐹 𝑛 𝐹(𝑛 − 1)
1 1
1 0
=
𝐹 𝑛 + 1 + 𝐹 𝑛 𝐹 𝑛 + 1
𝐹 𝑛 + 𝐹 𝑛 − 1 𝐹 𝑛
=
𝐹 𝑛 + 2 𝐹 𝑛 + 1
𝐹 𝑛 + 1 𝐹 𝑛

5. 證明-fast doubling
由矩陣表示式可知
𝐹 2𝑛 + 1 𝐹 2𝑛
𝐹 2𝑛 𝐹 2𝑛 − 1
=
1 1
1 0
2𝑛
=
1 1
1 0
𝑛 2
=
𝐹(𝑛 + 1) 𝐹(𝑛)
𝐹 𝑛 𝐹(𝑛 − 1)
2
=
𝐹(𝑛 + 1)2 + 𝐹(𝑛)2 𝐹(𝑛 + 1)𝐹(𝑛) + 𝐹(𝑛)𝐹(𝑛 − 1)
𝐹(𝑛)𝐹(𝑛 + 1) + 𝐹(𝑛 − 1)𝐹(𝑛) 𝐹(𝑛)2 + 𝐹(𝑛 − 1)2
比較前後式可得：
1 𝐹 2𝑛 + 1 = 𝐹(𝑛 + 1)2 + 𝐹(𝑛)2
2 𝐹 2𝑛 = 𝐹 𝑛 𝐹 𝑛 + 1 + 𝐹 𝑛 − 1
= 𝐹 𝑛 𝐹 𝑛 + 1 + 𝐹 𝑛 + 1 − 𝐹 𝑛
= 𝐹(𝑛)[2𝐹(𝑛 + 1) − 𝐹(𝑛)]

6. 演算法
Fast_Fib(n)
a = 0; b = 1; //m=0
for i = (number of binary digit in n) to 1
t1 = a*(2*b-a);
t2 = b^2 + a^2;
a = t1; b = t2; //m*=2
if(current binary digit == 1)
t1=a+b; //m++
a = b; b = t1;
return a;

7. 例: n = 10 = 10102
i start 4 3 2 1 result
n 1010
^
1010
^
1010
^
1010
^
F(m) F(0) F(0*2+1) F(1*2) F(2*2+1) F(5*2) F(10)
a 0 1 1 5 55 55
b 1 1 2 8 89

8. Assembly實作
 省略 F(0)，從F(1)開始
 clz：計算leading zeros以求位數
 cbz：if(Ra==0) goto label
 利用rsb (reverse subtract) + barrel shifter

10. 參考資料
 ARM instruction quick reference --
http://users.ece.utexas.edu/~valvano/Volume1/QuickRefe
renceCard.pdf
 Project Nayuki : Fast Fibonacci algorithms --
http://www.nayuki.io/page/fast-fibonacci-algorithms
 Wiki : Fibonacci number --
https://en.wikipedia.org/wiki/Fibonacci_number
 The first 300 Fibonacci numbers --
http://www.maths.surrey.ac.uk/hosted-
sites/R.Knott/Fibonacci/fibtable.html