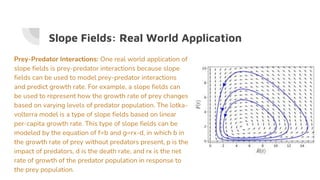
This document provides information about arc length and slope fields. It discusses arc length in three paragraphs, including its real-world applications in physics for studying particle nature and calculating travel distance. Slope fields are defined in three sentences. Real-world applications of slope fields include modeling prey-predator interactions and sales analysis. Careers that utilize arc length and slope fields, such as astronomy and meteorology, are discussed in two paragraphs.

1. Module Seven
Final Project
By: Nimansha Verma
05/04/2023

2. Topic 1: Arc Length
● Arc length is the distance between two
points along a section of a curve (the
distance you would travel if you were
walking along the path of the curve)
● We can draw tiny little tangent lines to
the curve at many different places along
the curve and thereby break down the
curve into tiny little straight lines.

3. Arc Length Real World Applications
Studying Particle Nature in Physics: One real world application
of arc length is studying particle nature. For example, suppose a
vector-valued function describes the motion of a particle in
space. In order to determine how far the particle has traveled
over a given time interval, it can be described by the arc length
of the path it follows. Similarly, given a smooth curve, such as a
plane or space curve, the arc length formula can be used to
describe the curve over a given interval in two or three
dimensional form. A smooth curve means that the vector-valued
function is differentiable with a non-zero derivative. The only
difference would be that for the space curve, there would be
three component functions instead of two because it would
three dimensional. The formula, however, can only be applied to
smooth curves because the soothness guarantees that the curve
has no cusps that could make the formula problematic.

4. Arc Length Real World Applications Continued
Travel Distance: Another real world application
of arc length is distance traveled when a rocket
launched along a parabolic path. Moreover,
suppose that the vector-valued function
describes a road we are building and we want to
determine how sharply the road curves at a given
point. This is described by the curvature of the
function at that point. We begin by calculating
the arc length of curves defined as functions of x,
then we examine the same process for curves
defined as functions of y, in which process is
identical, with the roles of x and y reversed.

5. Arc Length in Career
Astronomer: Astronomy is a natural science that studies celestial
objects and phenomena. It uses mathematics, physics, and chemistry
in order to explain their origin and evolution. An astronomer uses arc
length for many things such as finding the radius of the planets, sun,
and moon, finding the distance between two planets, estimating the
distance traveled by objects and planets in space, and calculating arc
length for a curve in space. Astronomers express their research in
mathematical terms so, when representing the distance of a smooth
curve for a theory about a space event, they can use the arc length
formula to represent this research in mathematical terms. Also,
astronomers use trigonometry to determine how far away from Earth
the stars and planets are. Therefore, is any places along the path are
smooth curves, astronomers can represent their information found
using the arc length formula.

6. Topic 2: Slope Fields
● Slope fields are a graphical representation of the solutions
to a first-order differential equation of a scalar function.
Solutions to a slope field are functions drawn as solid
curves.
● A first derivative expressed as a function of x and y gives
the slope of the tangent line to the solution curve that goes
through any point in the plane.
● For example, dy/dx=x+y so, by local linearity when we
zoom in close to (0, 1) the solution curve has to look a lot
like the line with slope one that passes through (0, 1).
● We know what the slope of the tangent line is at each
point in the plane. So, we can draw very short line
segments with the appropriate slope at each point in the
plane.

7. Slope Fields: Real World Application
Prey-Predator Interactions: One real world application of
slope fields is prey-predator interactions because slope
fields can be used to model prey-predator interactions
and predict growth rate. For example, a slope fields can
be used to represent how the growth rate of prey changes
based on varying levels of predator population. The lotka-
volterra model is a type of slope fields based on linear
per-capita growth rate. This type of slope fields can be
modeled by the equation of f=b and g=rx-d, in which b in
the growth rate of prey without predators present, p is the
impact of predators, d is the death rate, and rx is the net
rate of growth of the predator population in response to
the prey population.

8. Slope Fields Real World Application
Continued
Sales: Another real world application of slope
fields is for sales because many companies
use slope fields to manage and analyze the
sales that they have made per year. This is
possible because a slope field is a visual
representation of a differential equations so,
they can determines the nature of a function.

9. Slope Fields in Career
Meteorologist and Atmospheric Scientist: Research
meteorologists study atmospheric phenomena such as
lightning. Atmospheric scientists study the weather and
climate. They may compile data, prepare reports and forecasts,
and assist in developing new data collection instruments.
Meteorologist and atmospheric scientist use slope fields
because weather mapping technology uses programs similar to
slope fields to graph/show wind, temperatures, and moving
storm systems. Slope fields above, look very similar to the
vector, or directional wind maps. The difference is that instead
of singling out the solution at one point, most maps will show
all outcomes, or all of the wind patterns at the same time. Each
arrow points in the direction, or slope of the wind at that point.
If we group slope fields in with vector fields, then the process
of finding solutions and drawing the slope field model weather
patterns.

10. Works Cited
● https://math.libretexts.org/Bookshelves/Calculus/Map%3A_Calculus__Early_Transcendentals
_(Stewart)/08%3A_Further_Applications_of_Integration/8.03%3A_Applications_to_Physics_
and_Engineering
● https://www.bartleby.com/subject/math/calculus/concepts/arc-length
● https://resources.weboffice.vertigis.com/Documentation/WebOffice10R3/HTML/measure_arc
_length.htm
● https://prezi.com/uyk_zhr9171w/slope-fields/
● http://blogs.neisd.net/rkamata2020/2019/12/16/predicting-the-weather-how-slope-fields-
make-up-your-morning-news-
cast/#:~:text=Weather%20mapping%20technology%20uses%20programs,temperatures%2
C%20and%20moving%20storm%20systems.
● https://prezi.com/p8ezl_yllwta/slope-fields-application/
● https://teachingcalculus.com/2015/01/09/slope-fields/

11. The End!!!
Thank you for your time and
attention!