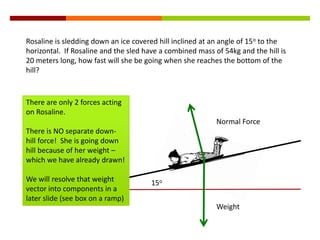
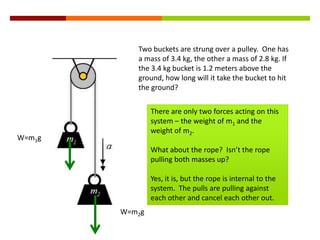
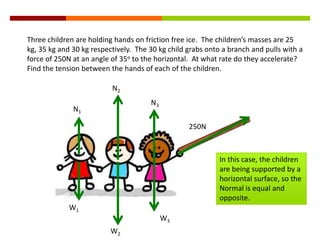
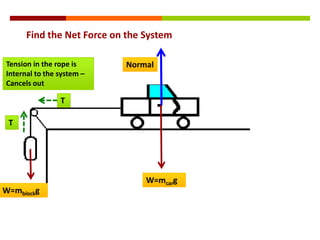
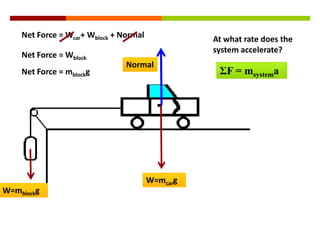
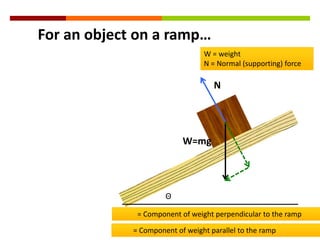
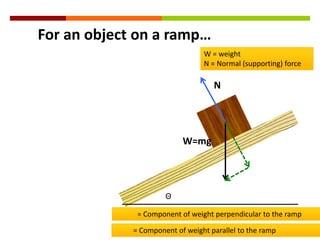
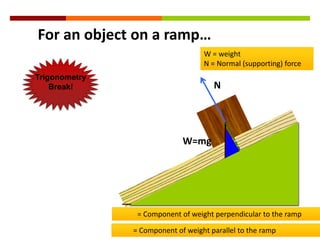
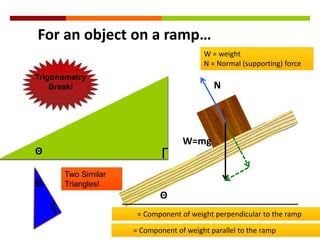
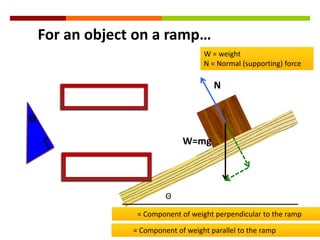
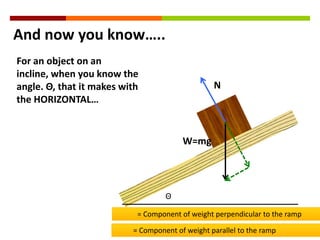
Newton's three laws of motion are summarized as follows: (1) an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force, (2) the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, and inversely proportional to the mass of the object, (3) for every action, there is an equal and opposite reaction. The document then provides examples of using free body diagrams and applying Newton's laws to solve various physics problems involving forces, motion, and kinematics.

1. Newton’s Three Laws of Motion(Cliff Notes Version)First law Inertia: a=0Second LawF=maThird Law Action-Reaction FA=-FR

2. Drawing Force DiagramsDraw all of the objects in the systemDraw the weight (w=mg)Draw the supporting Forces (N, T)The normal force is always drawn perpendicular to the supporting surface. It may not be equal to the weight – only when the object is completely supported by the normal is it equal in magnitude.Draw any additional external forces

3. Rosaline is sledding down an ice covered hill inclined at an angle of 15o to the horizontal. If Rosaline and the sled have a combined mass of 54kg and the hill is 20 meters long, how fast will she be going when she reaches the bottom of the hill?There are only 2 forces acting on Rosaline. There is NO separate down-hill force! She is going down hill because of her weight – which we have already drawn!We will resolve that weight vector into components in a later slide (see box on a ramp)Normal Force15oWeight

4. Two buckets are strung over a pulley. One has a mass of 3.4 kg, the other a mass of 2.8 kg. If the 3.4 kg bucket is 1.2 meters above the ground, how long will it take the bucket to hit the ground? There are only two forces acting on this system – the weight of m1 and the weight of m2. What about the rope? Isn’t the rope pulling both masses up? Yes, it is, but the rope is internal to the system. The pulls are pulling against each other and cancel each other out.W=m1gW=m2g

5. Three children are holding hands on friction free ice. The children’s masses are 25 kg, 35 kg and 30 kg respectively. The 30 kg child grabs onto a branch and pulls with a force of 250N at an angle of 35o to the horizontal. At what rate do they accelerate? Find the tension between the hands of each of the children. N2N3N1250NIn this case, the children are being supported by a horizontal surface, so the Normal is equal and opposite. W1W3W2

6. In a clever attempt to foil the enemy, James Bond (mass 85 kg) skis down a hill that makes a 23.0o angle and is 15 meters in length. He then skis on a level surface for 10 meters until he skis off of a cliff that is 6 meters high and lands in a moving snowmobile. The snowmobile travels at a constant rate of 2 m/sec in a direction parallel to James’ path of decent If James and the snowmobile start at the same point in time, how far from the base of the “catch point” must the snowmobile start? NormalSame as Problem #123.0oWeight

7. Find the Net Force on the SystemNormalTension in the rope is Internal to the system – Cancels outTTW=mcargW=mblockg

8. Net Force = Wcar+ Wblock + NormalAt what rate does the system accelerate?Net Force = WblockNormalΣF = msystemaNet Force = mblockgW=mcargW=mblockg

9. For an object on a ramp…W = weight N = Normal (supporting) forceNW=mgΘ = Component of weight perpendicular to the ramp = Component of weight parallel to the ramp

10. For an object on a ramp…W = weight N = Normal (supporting) forceNW=mgΘ = Component of weight perpendicular to the ramp = Component of weight parallel to the ramp

11. For an object on a ramp…W = weight N = Normal (supporting) forceTrigonometryBreak!NW=mgΘ = Component of weight perpendicular to the ramp = Component of weight parallel to the ramp

12. For an object on a ramp…W = weight N = Normal (supporting) forceTrigonometryBreak!NW=mgΓΘTwo Similar Triangles!ΘΘΓ = Component of weight perpendicular to the ramp = Component of weight parallel to the ramp

13. For an object on a ramp…W = weight N = Normal (supporting) forceNΘΓW=mgΘ = Component of weight perpendicular to the ramp = Component of weight parallel to the ramp

14. And now you know…..For an object on an incline, when you know the angle. Θ, that it makes with the HORIZONTAL…NW=mgΘ = Component of weight perpendicular to the ramp = Component of weight parallel to the ramp

15. Analyzing the Force DiagramsGoal: Find the Net ForceGoal 2: Use the net force to find AccelerationGoal 3: Use acceleration to answer kinematics Questions

16. The EndAnswers to Problem Set 21-2210 m/s1.6 sec2.3 m/sec2, 138N and 58N9.7m