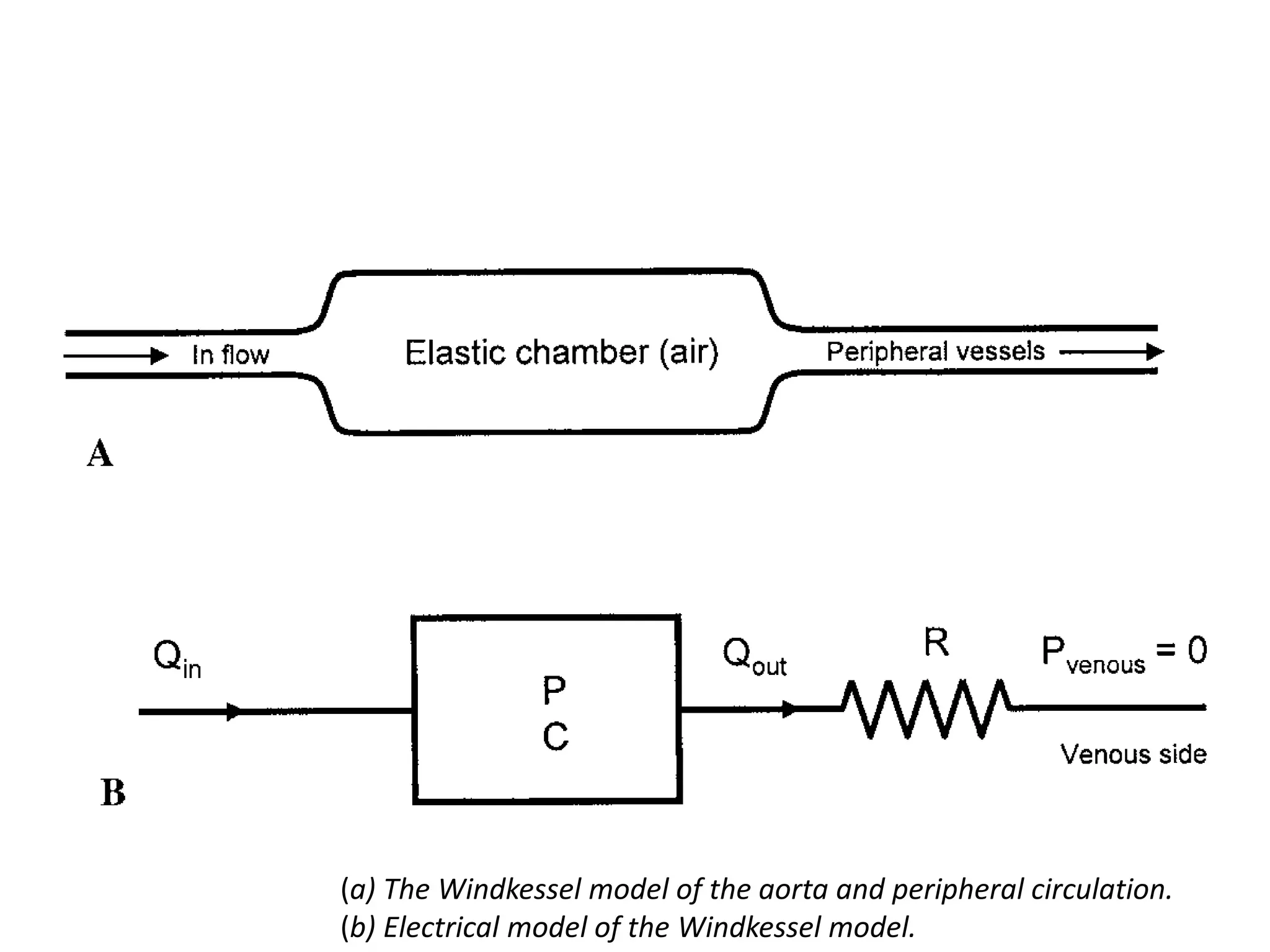
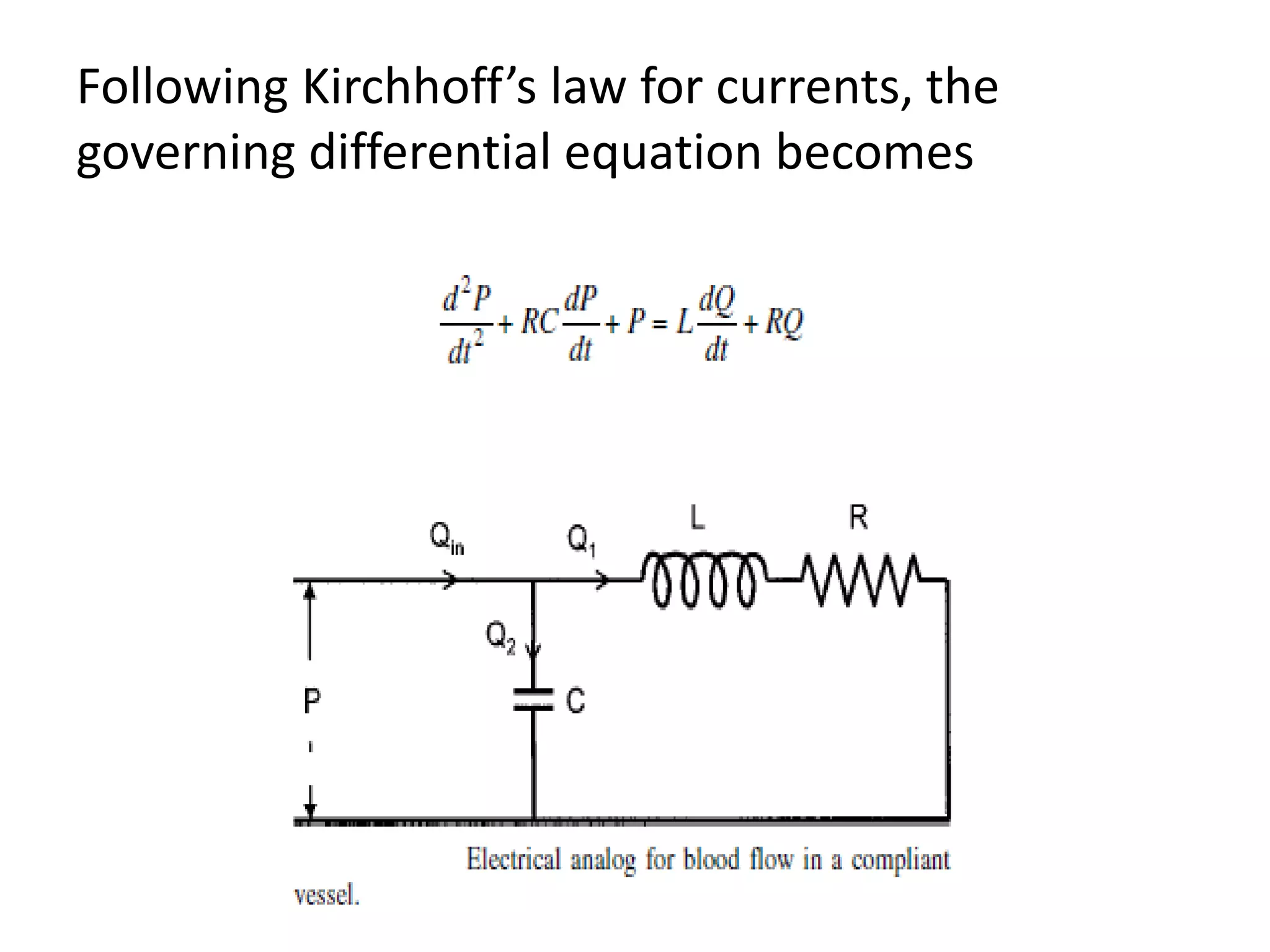
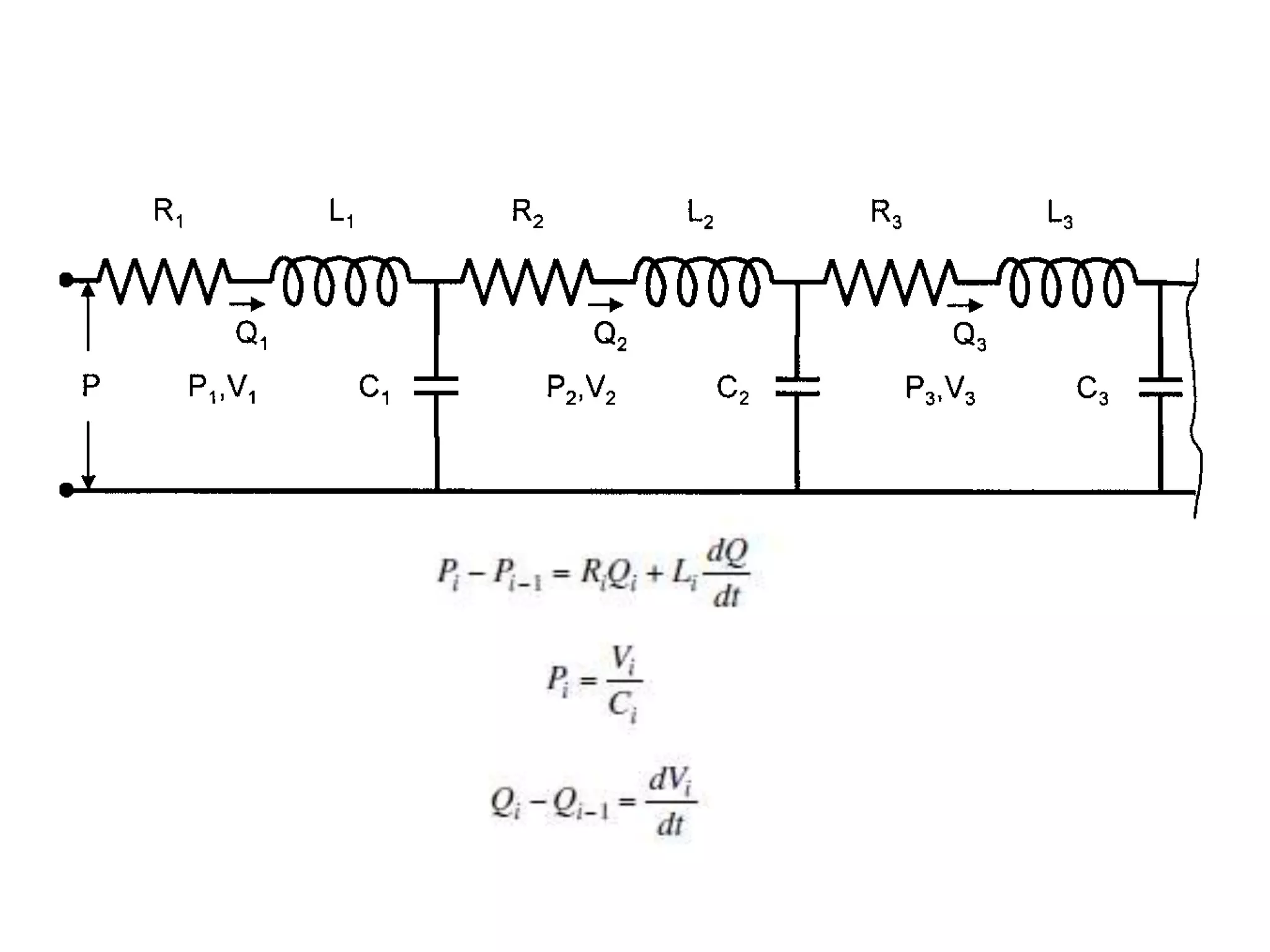
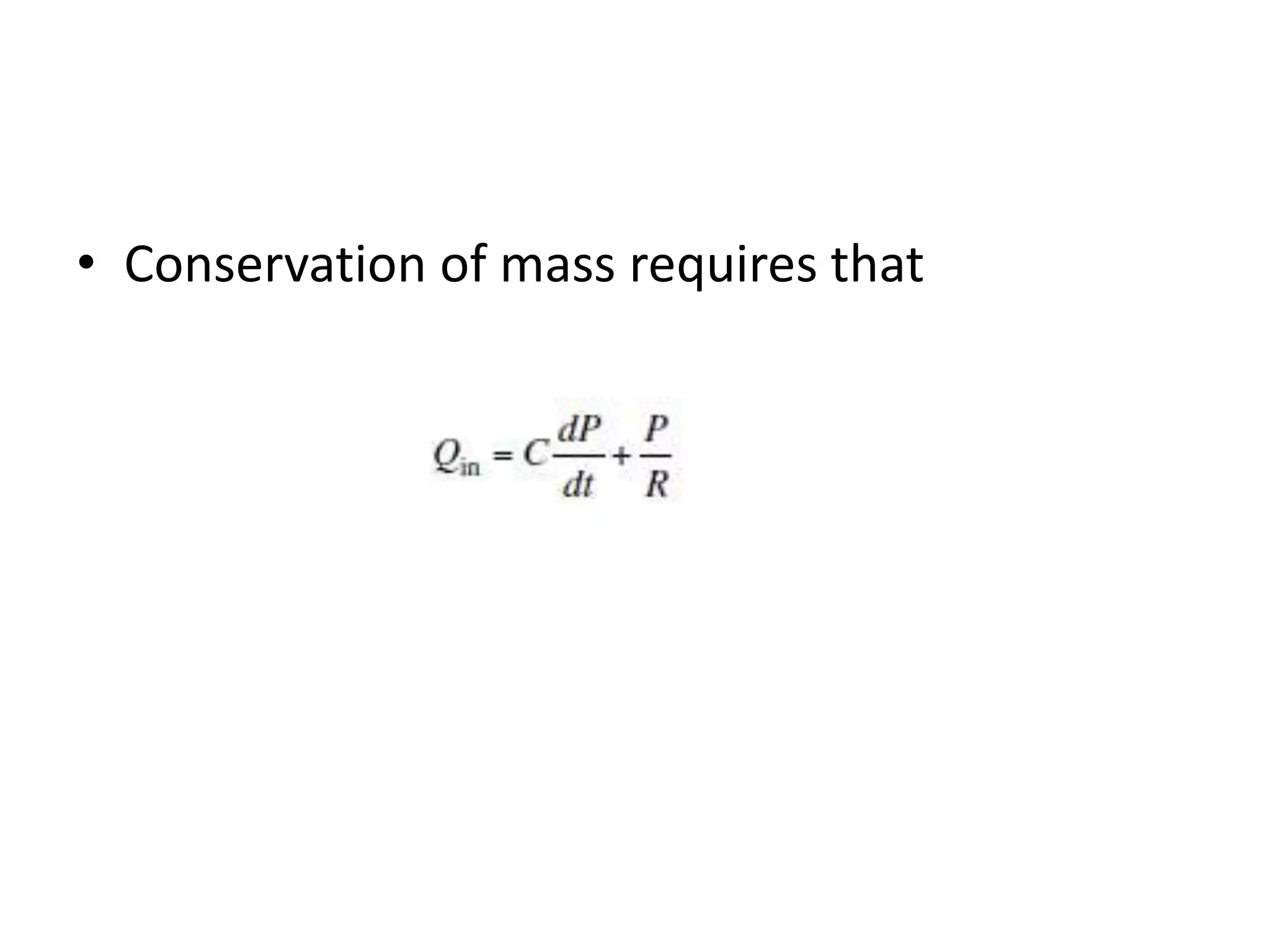The document describes two analog models used to model blood flow: mechanical and electrical models. The mechanical (Windkessel) model represents the aorta and peripheral vessels as a compliant air cell and rigid tube with resistance. Blood flow and pressure are modeled with linear equations. The electrical model represents vessel resistance as resistors, compliance as capacitors, and inertia as inductors to investigate blood flow phenomena through analogous linear differential equations. Kirchhoff's law is then used to derive the governing differential equation.

1. ANALOG MODELS OF BLOOD
FLOW
Gilu Francis

2. Mechanical Models (Windkessel)
• Suggested by Otto Frank (1899)
• The aorta and large blood vessels are represented
by a linear compliant air-cell
• Peripheral vessels are replaced by a rigid tube
with a linear resistance
• V= C. P
• Qout =P/R
• where V, P, and C = volume, pressure, and compliance of the
air-cell and are linearly related
• Qout = outflow of the air-cell
• R = linear resistance of the rigid tube
• Pvenous = 0

3. (a) The Windkessel model of the aorta and peripheral circulation.
(b) Electrical model of the Windkessel model.

4. • Conservation of mass requires that

5. Electrical Models
• In order to investigate linear approximations of
complex blood flow phenomena, electrical analogs,
which result in analogous linear differential equations,
were developed (Dinnar, 1981).
• In these models the vessel resistance to blood flow is
represented by a resistor R, the tube compliance by a
capacitor C, and blood inertia by an inductance L.
Assuming that blood flow and pressure are analogous
to the electrical current and voltage, respectively,
blood flow through a compliant vessel (e.g., artery or
vein) may be represented by an electrical scheme.

6. Following Kirchhoff’s law for currents, the
governing differential equation becomes