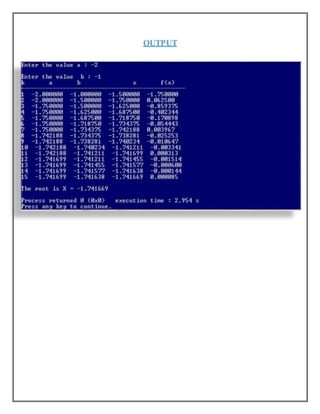
The document outlines steps for finding the root of a function using the bisection method. It defines a function f(x), reads bounds a and b, calculates the midpoint xk between a and b, evaluates f(xk), and updates the bounds based on the sign of f(a) and f(xk). It repeats until the difference between iterations is less than a tolerance value, then prints the root.

2. Steps Task
01 Define ( )f x
02 Read a ‘The lower bound of the desired roots’
03 Read b ‘The upper bound of the desired roots’
04 Set 1k 
05 Calculate
2
k
a b
x


06 Calculate  k kf f x
07 Print , ,k kk x f
08 If 1 0.0001k kx x   then
GOTO Step 11
Else if
 . 0kf a f  then kb x .
Else
 . 0kf b f  then ka x .
End if
09 Set 1k k 
10 GOTO Step 05
11 Print ‘Required root, kx ’
12 STOP

3. #include<stdio.h>
#include<math.h>
#define eqn x*x-4*x-10
#define esp 0.0001
float f(float x)
{
float ans;
ans=eqn;
return ans;
}
int main()
{
float a,b;
int k=1;
printf("nEnter the value a : ");
scanf("%f",&a);
printf("nEnter the value b : ");
scanf("%f",&b);
float xk,fk;
if(f(a)*f(b)>=0)
{
printf("nWrong Interval");
return;
}

4. printf("ktatbttxtf(x)n");
printf("-----------------------------------------------n");
while(k)
{
xk=(a+b)/2;
fk=f(xk);
printf("%d %f %f %f %f n",k,a,b,xk,fk);
if(fabs(f(xk))<esp)
{
printf("nThe root is X = %f n",xk);
break;
}
else if(f(a)*fk<0)
{
b=xk;
}
else
{
a=xk;
}
k++;
}
}

5. OUTPUT