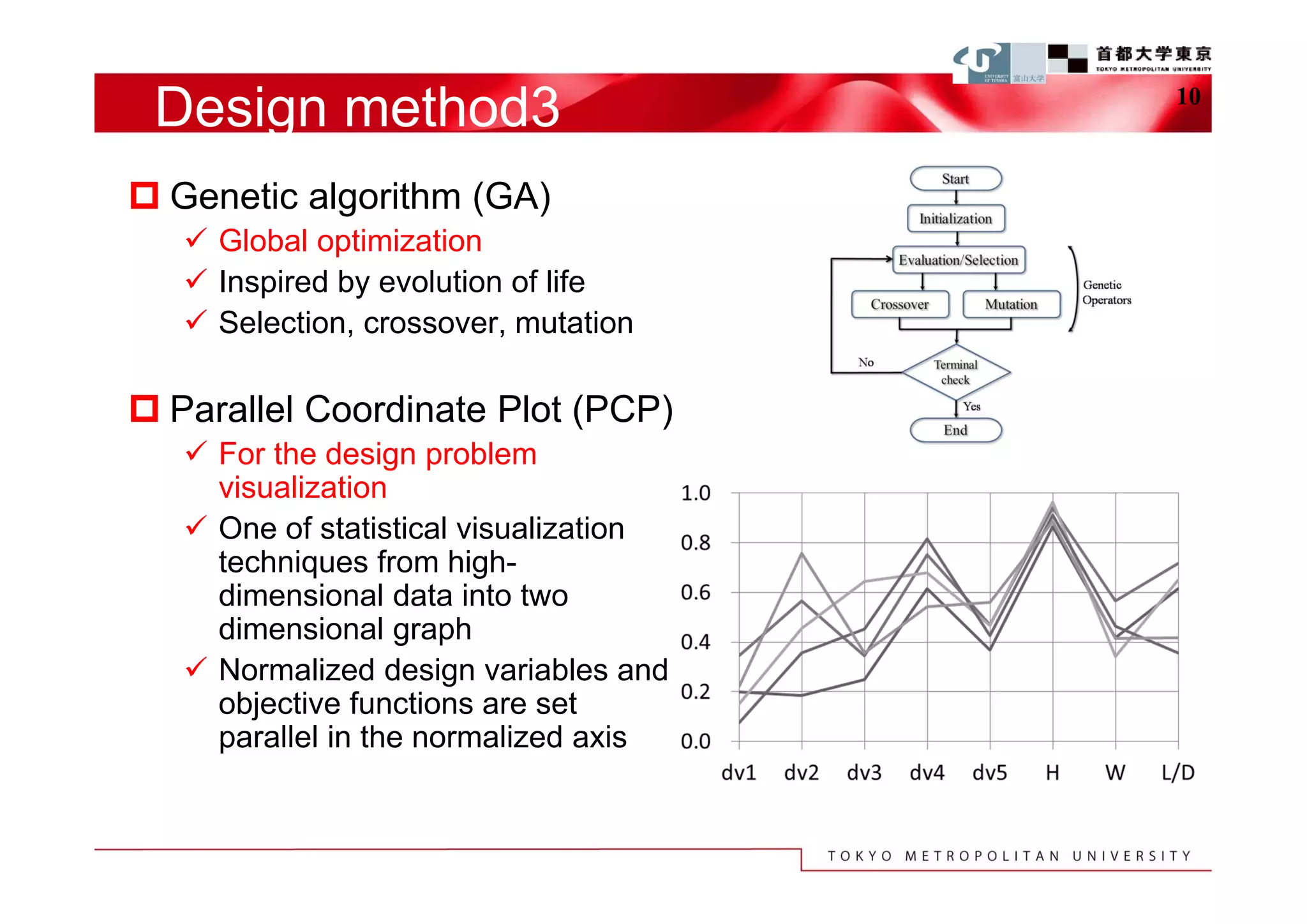
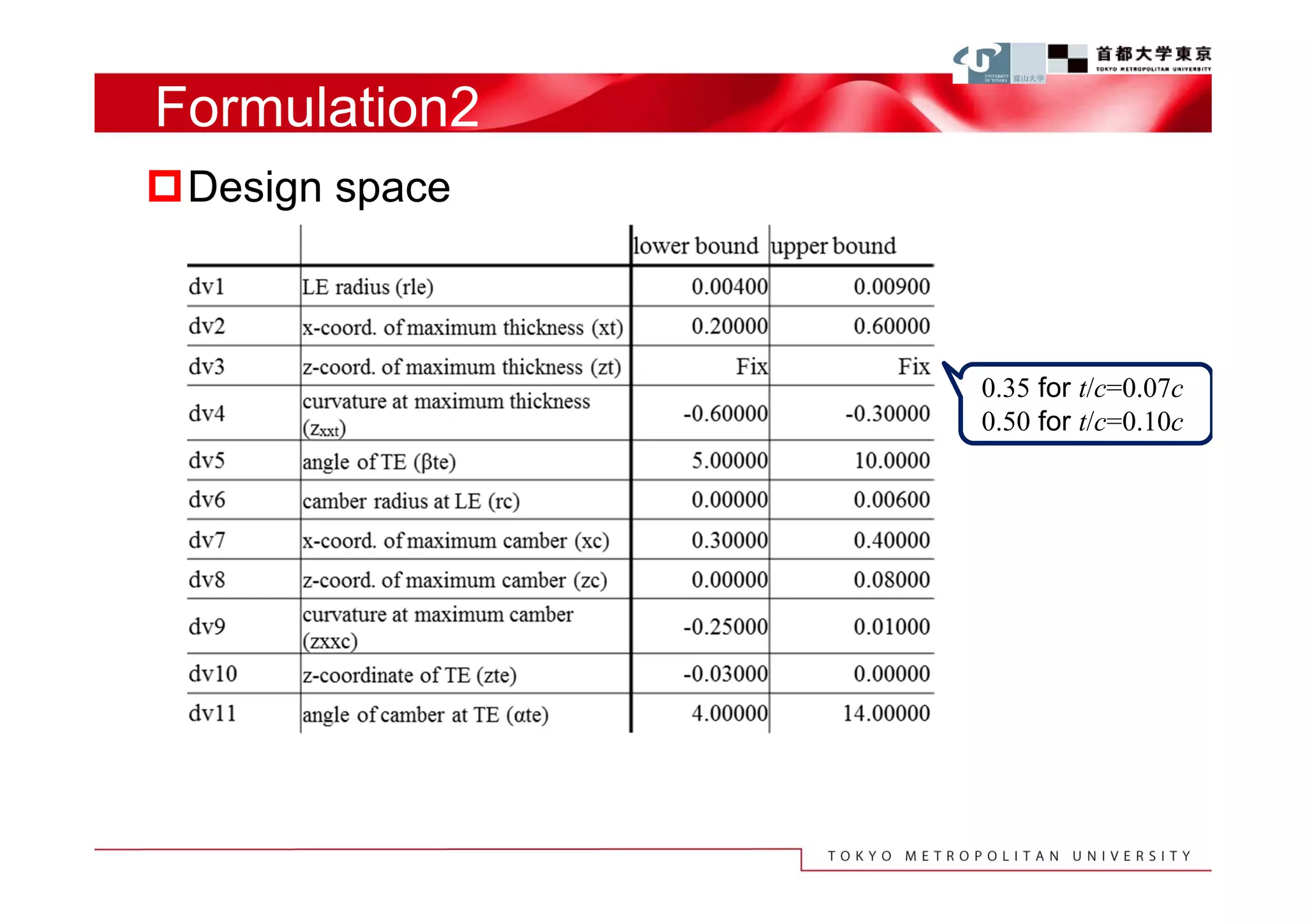
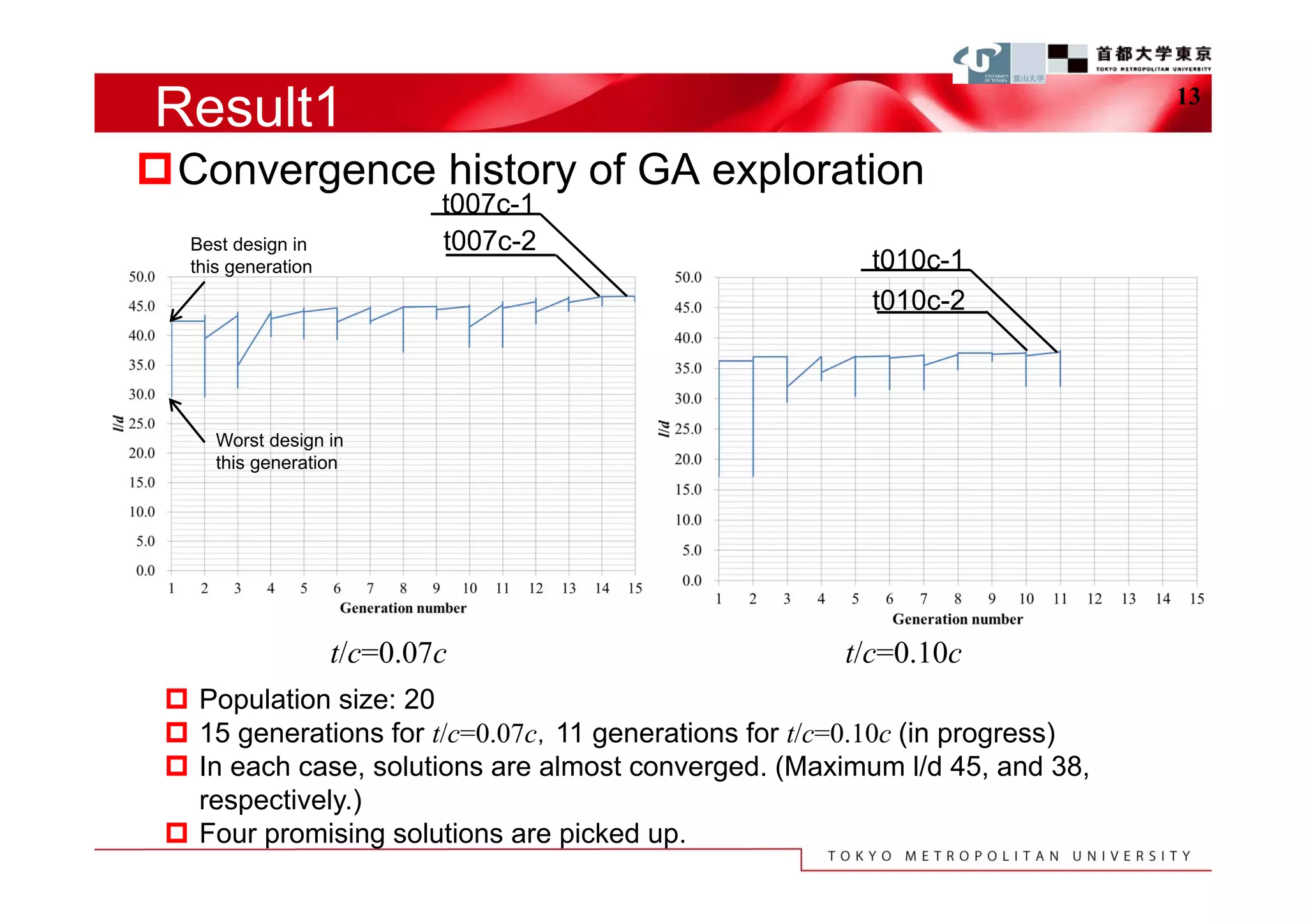
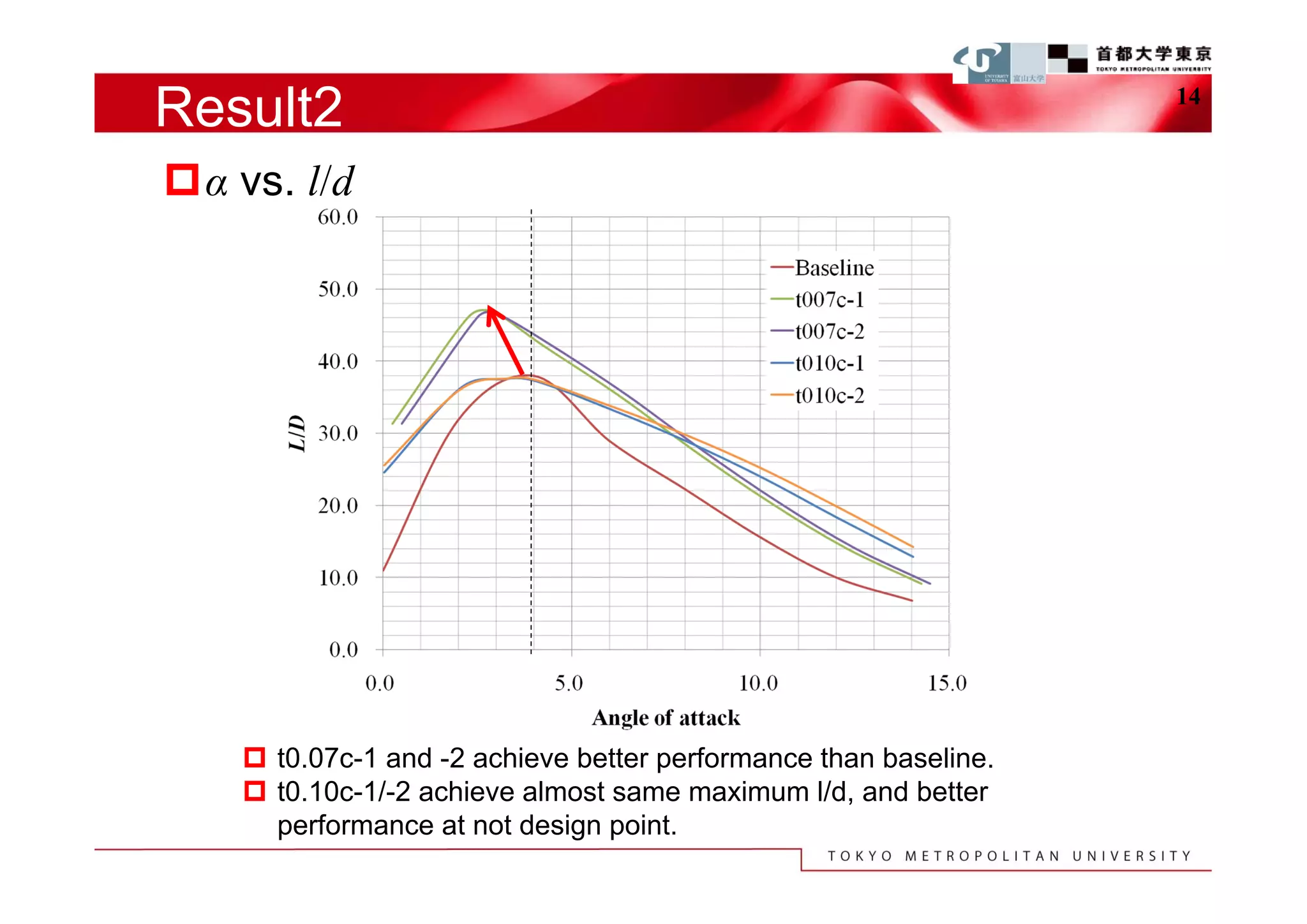
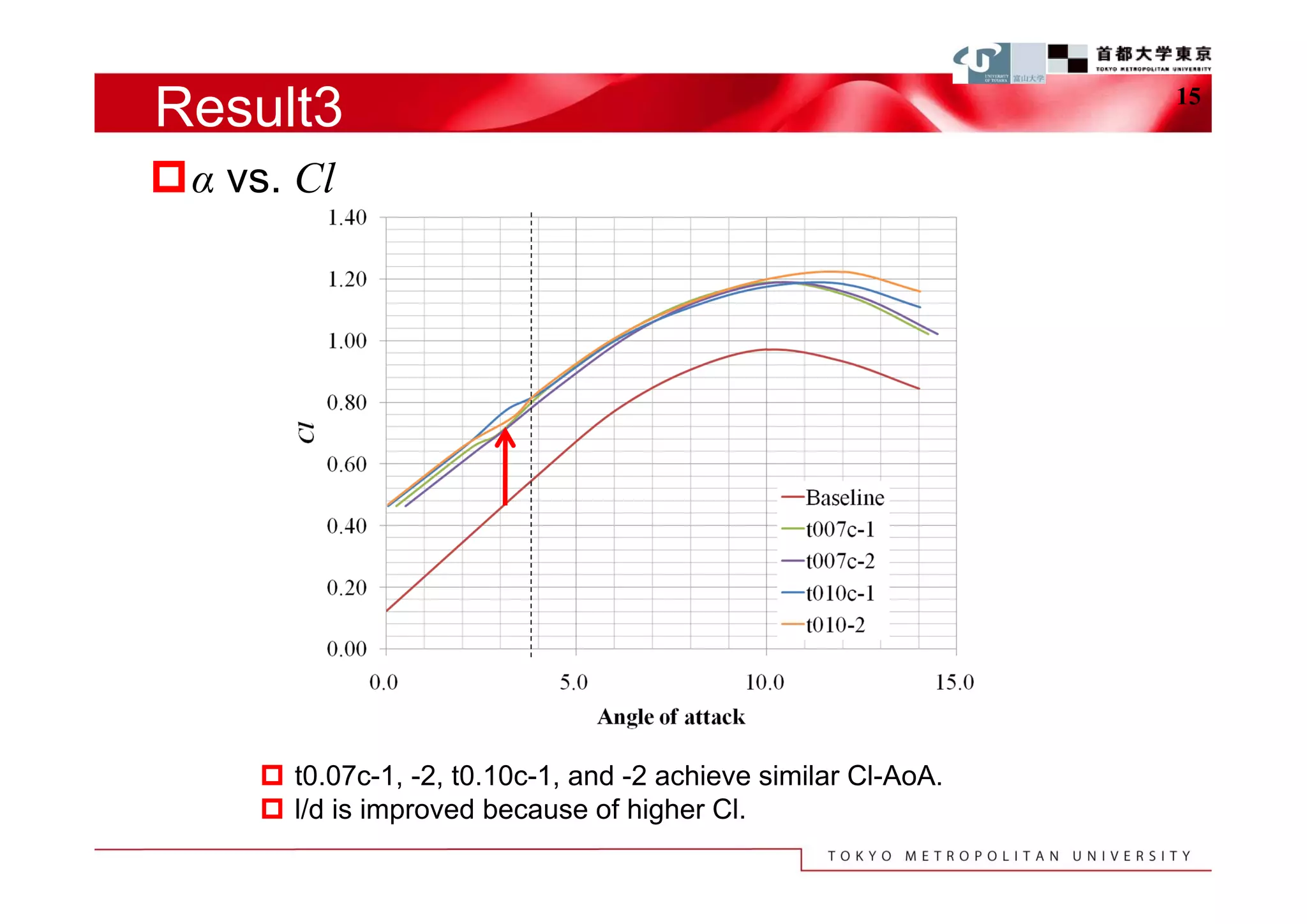
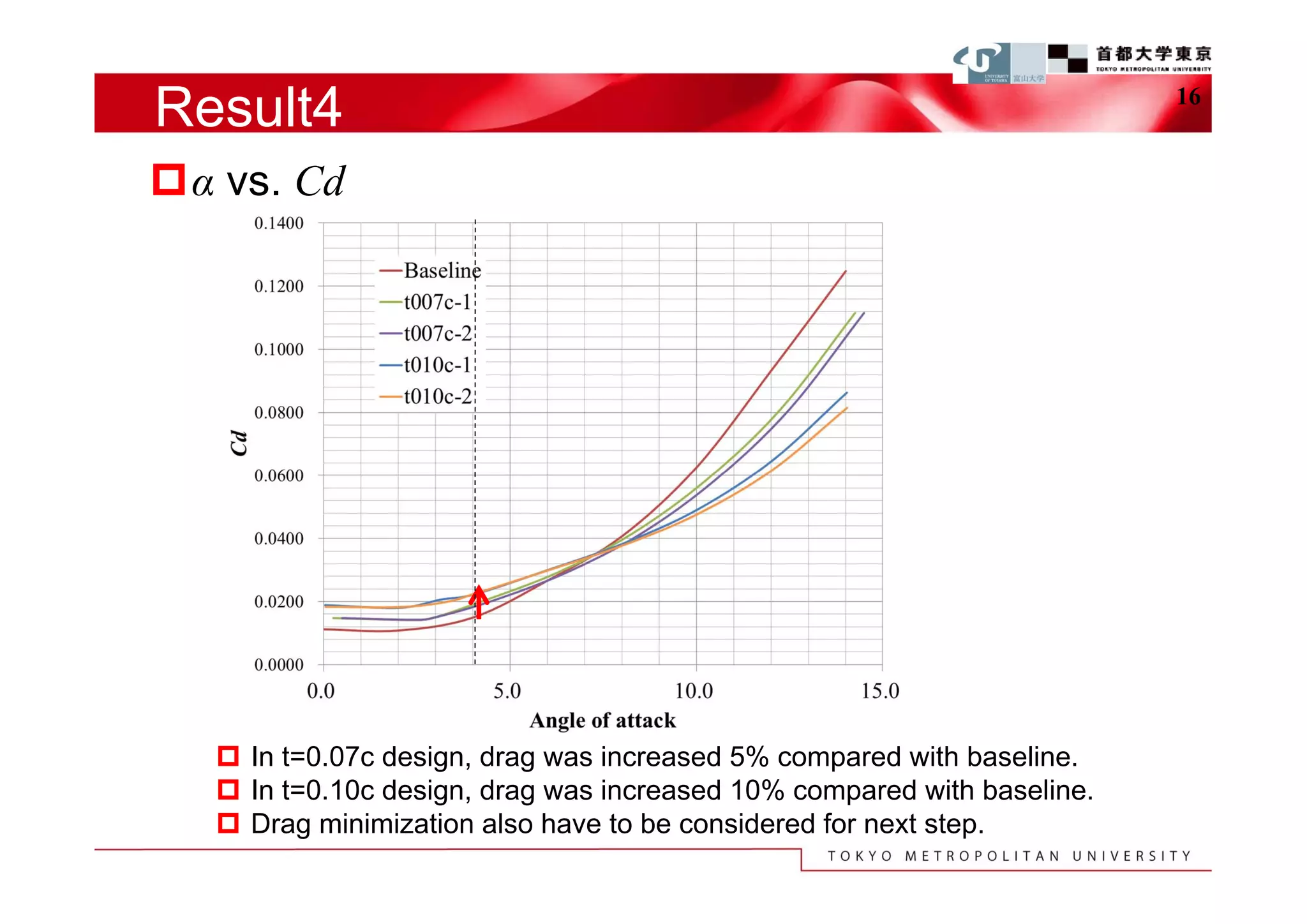
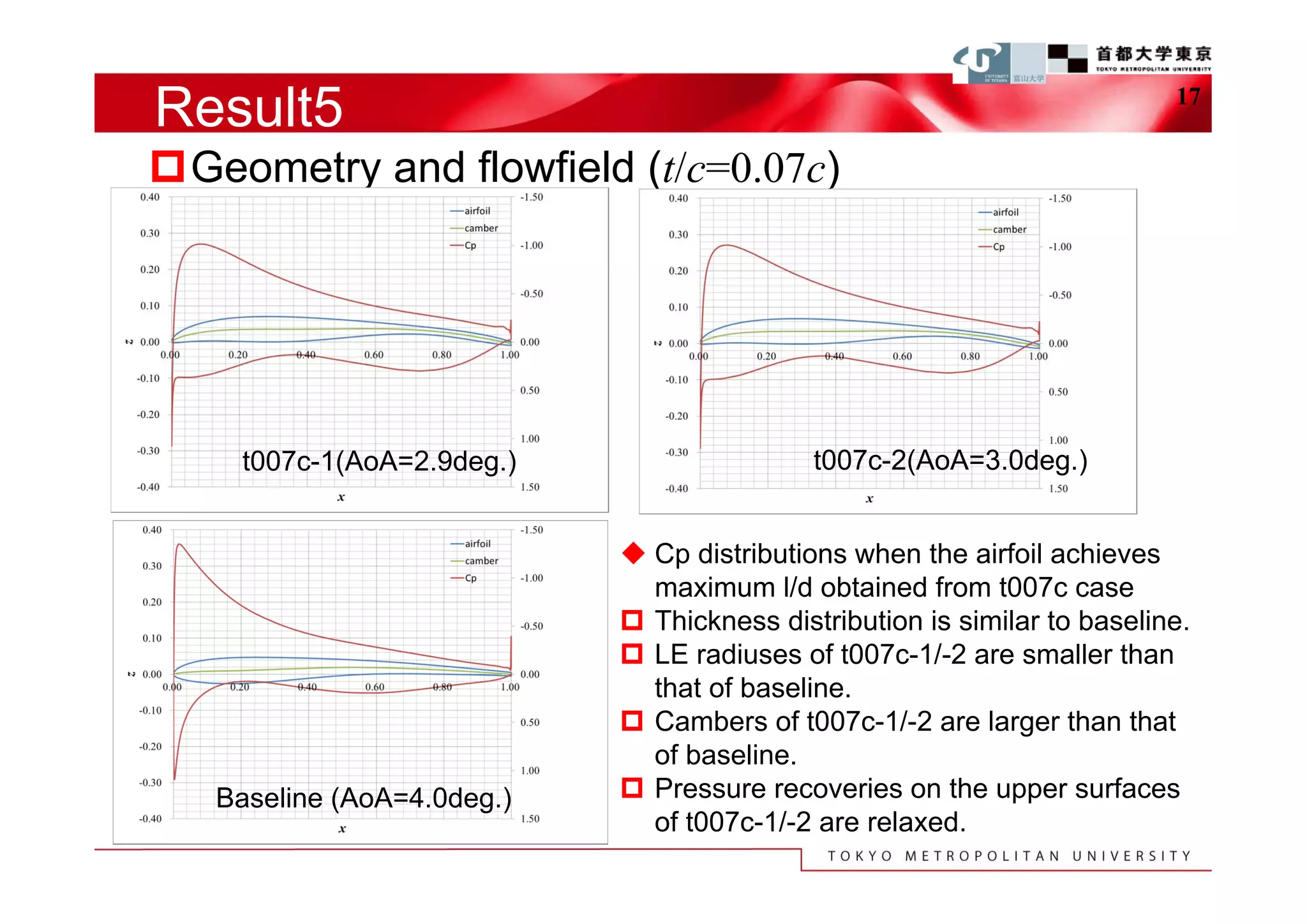
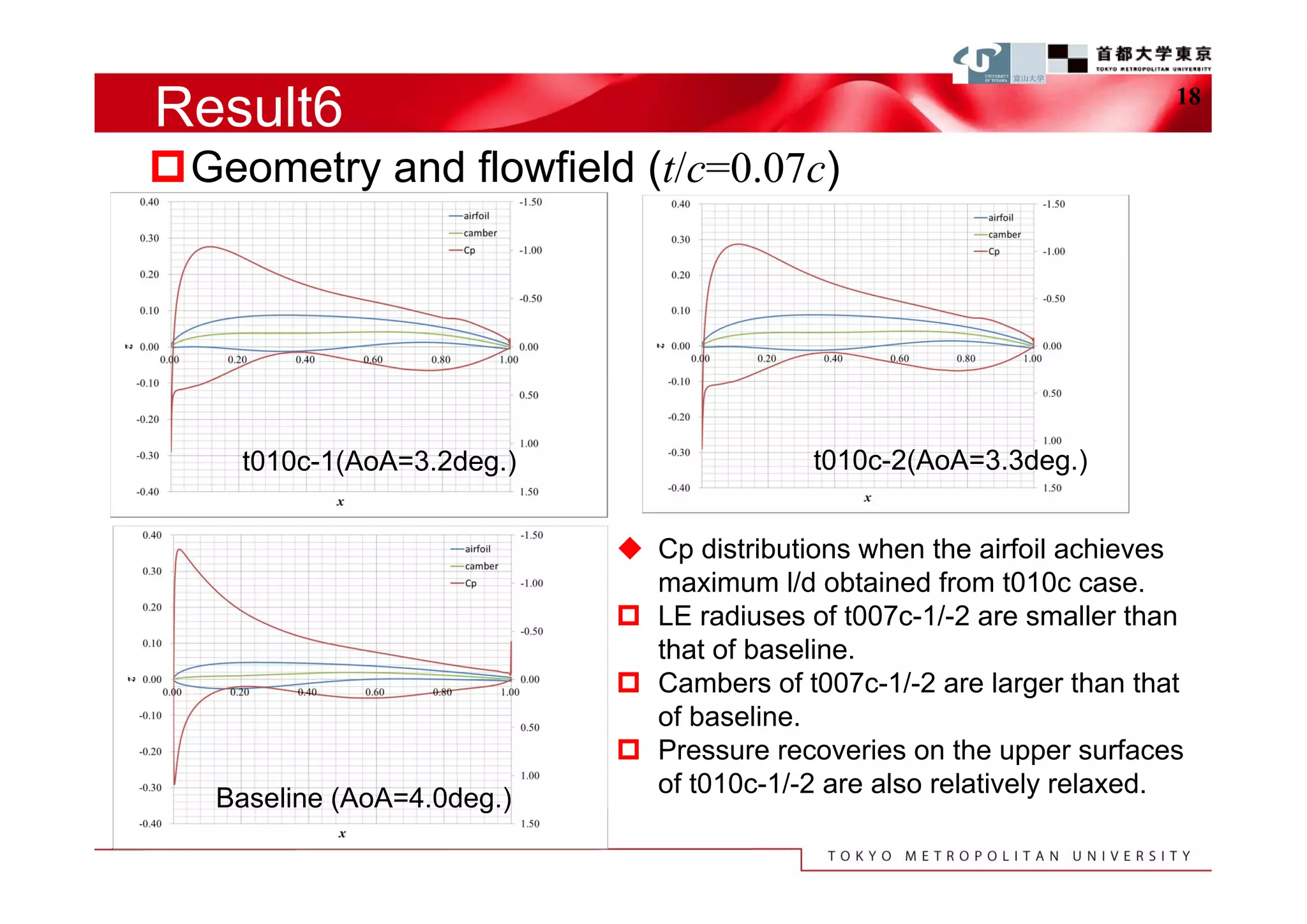
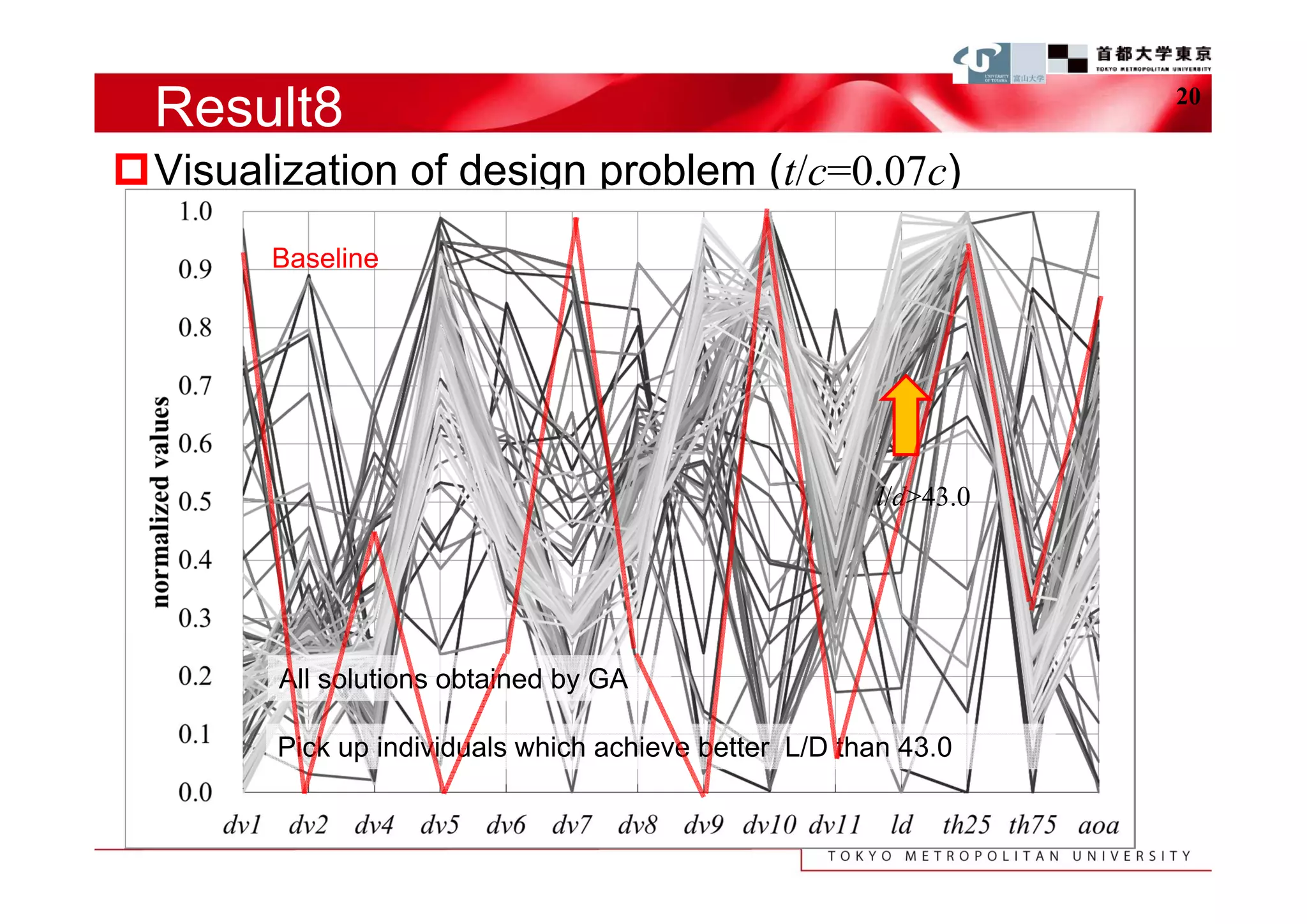
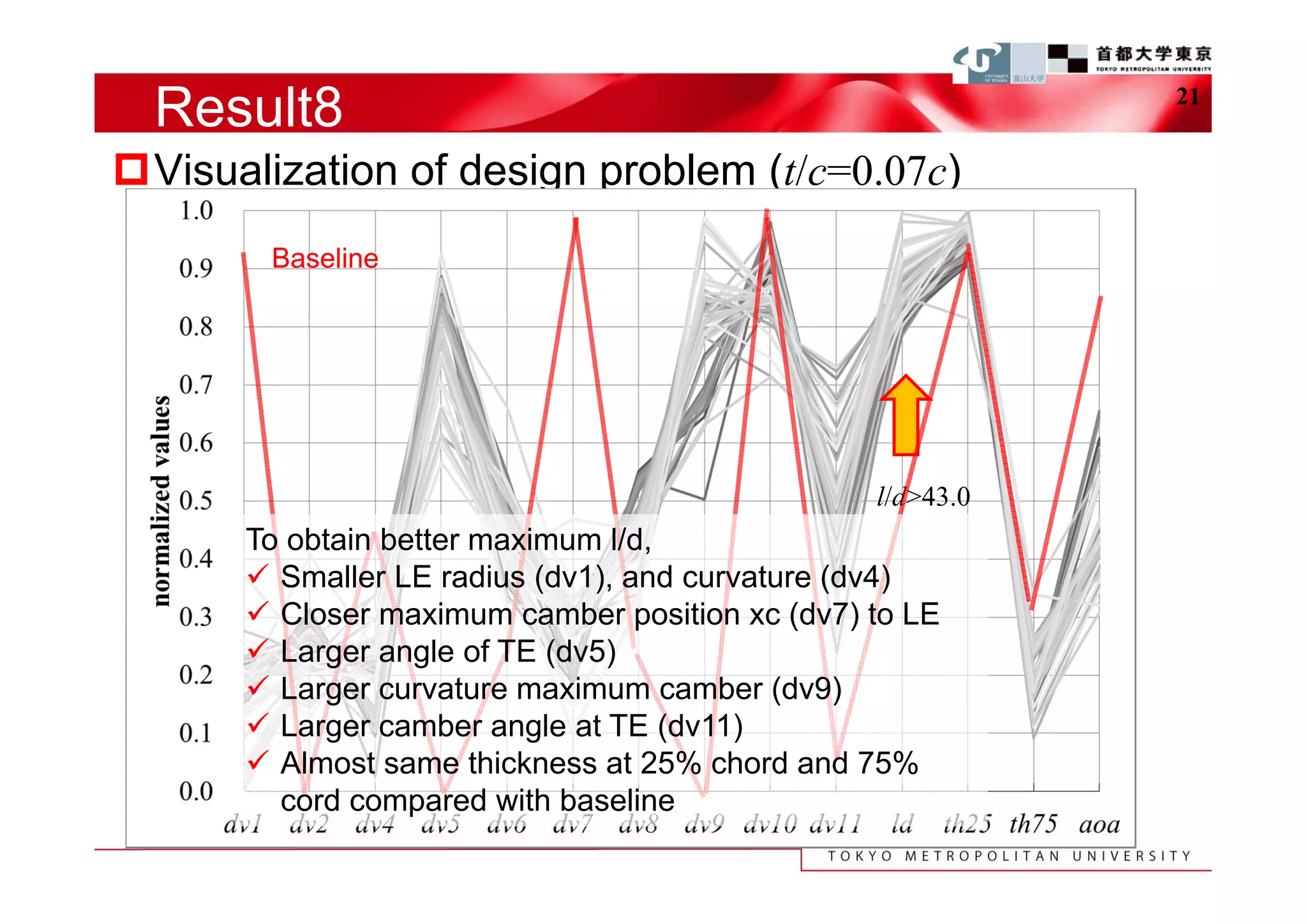
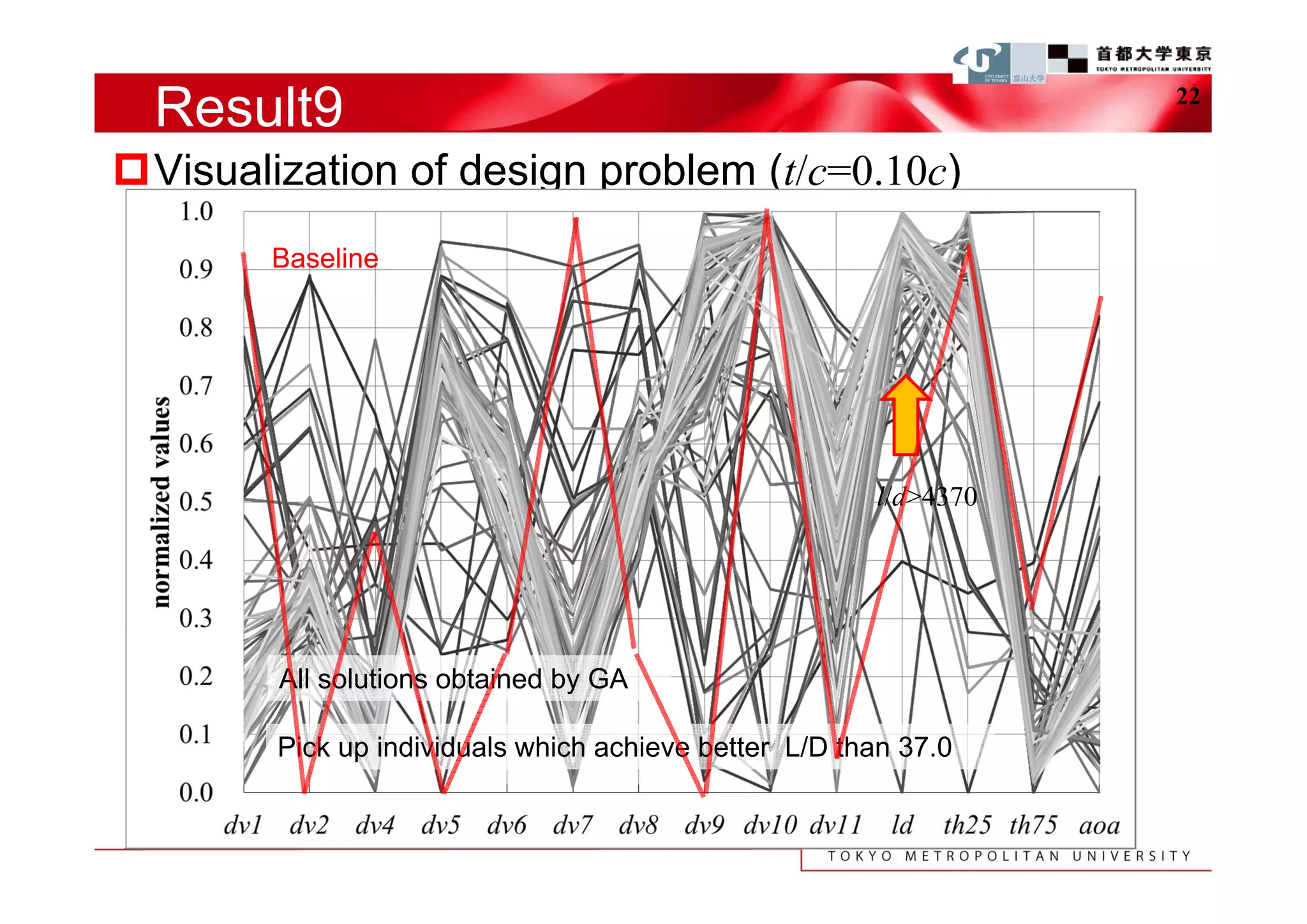
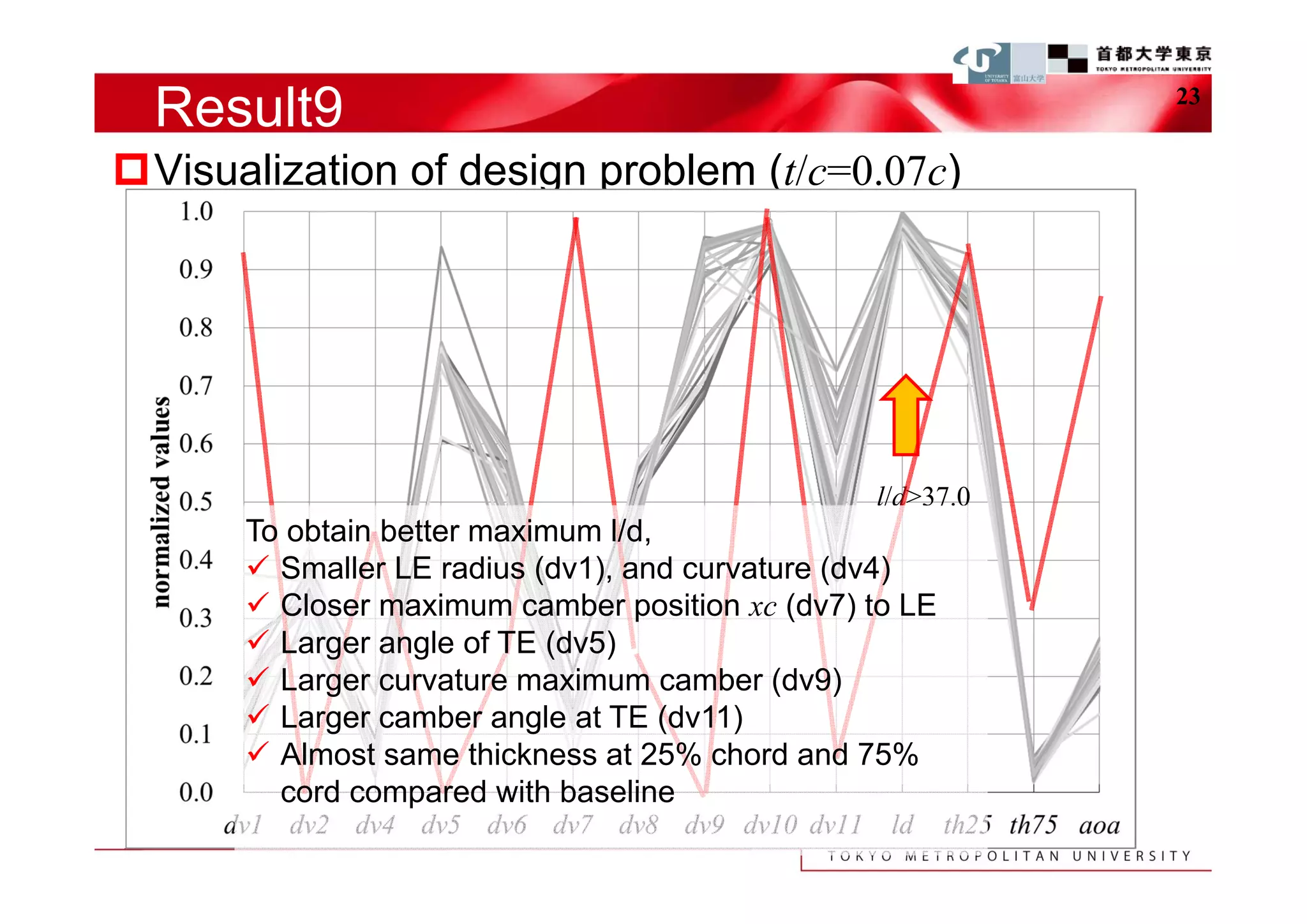
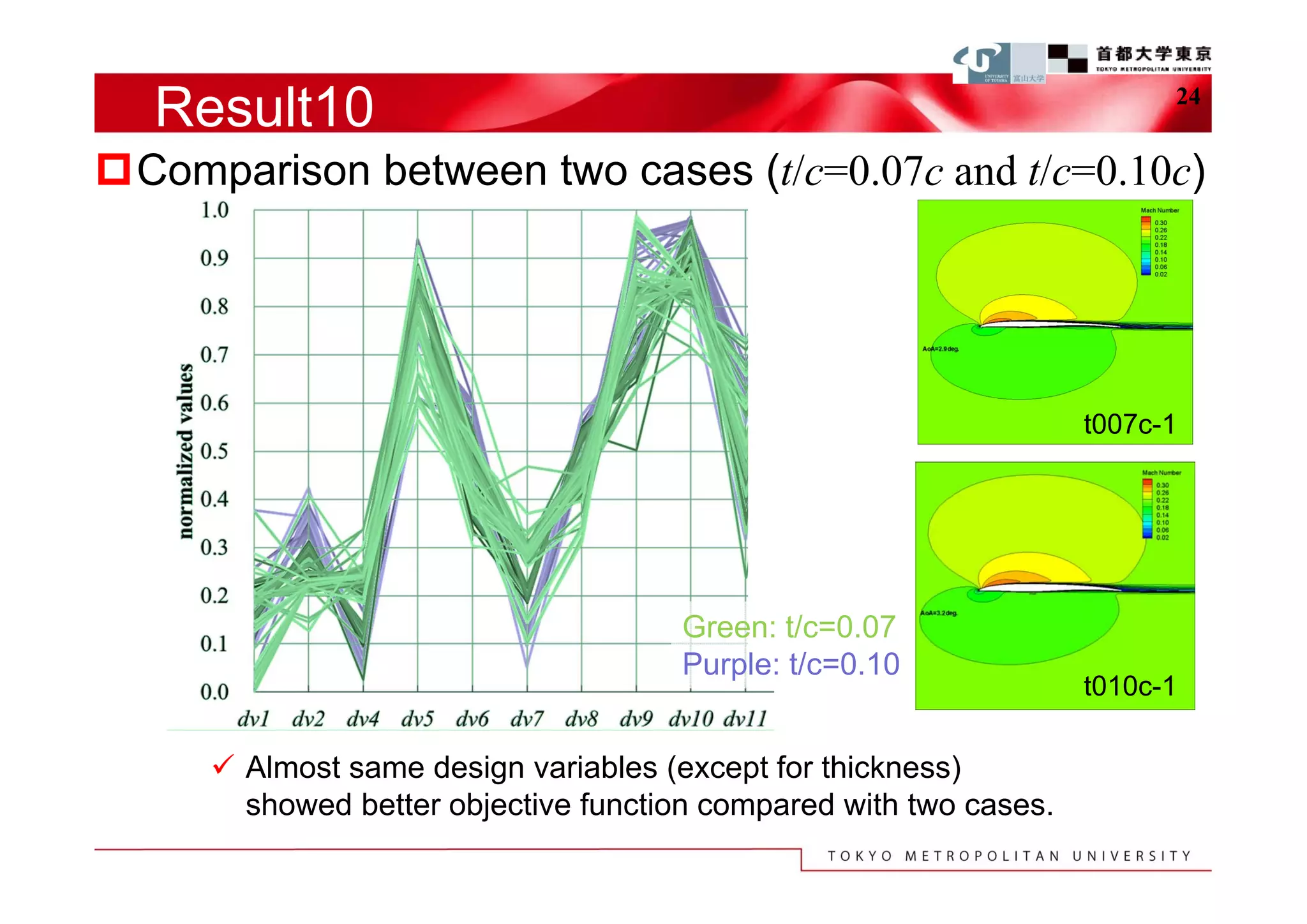
The document describes a study that used computational fluid dynamics and genetic algorithms to optimize airfoil designs for aircraft intended to fly on Mars. The study represented airfoils using a modified PARSEC method and evaluated designs based on their maximum lift-to-drag ratio. The optimization process produced designs with higher lift-to-drag ratios than the baseline design, achieving this through design changes like smaller leading edge radii, increased camber, and more relaxed upper surface pressure recovery. Visualization of the results provided insight into which design parameters most affected lift-to-drag ratio. The study demonstrated an efficient method for exploring unknown airfoil design problems to achieve higher performing designs for Mars aircraft.

1. Airfoil Design for Mars Aircraft
Using Modified PARSEC Geometry Representation
Masahiro Kanazaki
Tokyo Metropolitan University
Tomoyoshi Yotsuya
Tokyo Metropolitan University
Kisa Matsushima
University of Toyama

2. Contents 2
 Background
 Objectives
 Design methods
 Airfoil representation by modified PARSEC method
 Evaluation by computational fluid dynamics (CFD)
 Design optimization by genetic algorithm (GA)
 Knowledge discovery by scatter plot matrix (SPM)
 Formulation
 Results
 Maximization result of maximum lift to drag ratio (t/c=0.07c, 0.10c)
 Visualization result by Parallel Coordinate Plot (PCP)
 Conclusions

3. Background1 3
Image of MELOS  ”Mars airplane” is proposed
as a part of the MELOS.
 Technical challenges
 Propulsion
 Aerodynamic design
 Structure
・What kind of airfoil/wing
geometry achieves higher
performance?
・Ishii airfoil is one of the promising
design.

4. Background2 4
Difficulty of flight in the Martian atmosphere
gravity density Viscosity Sonic speed atmospheric
[m/s2] [kg/m3] [10-5Pa・s] [m/s] constituent
The Earth 9.8 1.17 1.86 345 N2，O2
The Mars 3.2 0.0118 1.36 258 CO2
 1/3 gravity of the earth → Required lift is 1/3.
 1% density of the earth → Lift is required to be
hundredfold increased.
⇒ Lift of the Mars-airplane have to be about 33rd
times lift as much as that of the Earth-airplane.
3/4 speed of sound → Compressibility should be
considered even for relative slow flight.
 Knowledge has to be acquired for unknown design problem.
 Efficient design method is required for Mars-airplane design.

5. Background3 5
Airfoil representations for unknown design problem
 B-spline curve, NURBS
 Good for use in CAD software
 Not good for use with data mining
 PARSEC(PARametric SECtion) method*
 Parameterization geometrical character
based on knowledge of transonic flow
 Separately definition upper surface
and lower surface
 Easy to introduce automated design
method such as genetic algorithm
 Aerodynamic performances can be
explained based on design variables.
 A few geometrical parameters around the
leading-edge
*Sobieczky, H., “Parametric Airfoils and Wings,” Notes on Numerical Fluid Mechanics, pp. 71-88, Vieweg 1998.

6. Background4 6
Modification of PARSEC representation**
 Separately defined thickness distribution and camber
 This definition is in theory of wing section
 Successful representation of supersonic airfoil
 Maintain the beneficial feature of original PARSEC
 A few numbers of design variables
 Aerodynamic performances can be explained by design
variables.
** K. Matsushima, Application of PARSEC Geometry Representation to High-Fidelity Aircraft Design by CFD,
proceedings of 5th WCCM/ ECCOMAS2008, Venice, CAS1.8-4 (MS106), 2008.

7. Objectives 7
Design exploration of airfoil for Mars-airplane
using modified PARSEC airfoil representation
Design exploration using CFD and GA
Selection of promising designs and
comparisons of their performances with
baseline (Ishii airfoil)
Knowledge discovery by means of PCP

8. Design methods1 8
 Airfoil representation by modified PARSEC method
 Designed by thickness distribution and camber .
 The leading edge radius center is always on the camber.
 The thickness distribution is same as symmetrical airfoil by PARSEC.
 The camber is defined by a quintic equation.
 By adding the root term for root camber, the design performance of the
leading-edge is improved.
 Number of design variables is 12.
Thickness 6 Camber
2 n1 5
z t   an  x 2
zc  b0  x   bn  x n
n 1 n 1
＋

9. Design method2 9
Evaluation by CFD
 Two dimensional Reynolds averaged Navier-Stokes flow
solver (RANS)

 QdV  F  nds  0
t 
 Time integration : LU-SGS implicit method
 Flux evaluation : Third-order-accuracy upwind differential
scheme with MUSCL method
 Turbulent model : Baldwin-Lomax model
 Grid : C-H type structured grid
 Grid size: 11,651 points
Computational grid

10. Design method3 10
 Genetic algorithm (GA)
 Global optimization
 Inspired by evolution of life
 Selection, crossover, mutation
 Parallel Coordinate Plot (PCP)
 For the design problem
visualization
 One of statistical visualization
techniques from high-
dimensional data into two
dimensional graph
 Normalized design variables and
objective functions are set
parallel in the normalized axis

11. Formulation1
Design problem (Single objective)
Maximize maximum L/D
subject to t/c=target t/c (t/c=0.07c, 0.10c)
Computational condition
Martian atmosphere
Density=0.0118kg/m3
Temperature=241.0K
Speed of sound=258.0m/s
Free stream
Velocity=60m/s
Reynolds number：208,235.3
Mach number：0.233

12. Formulation2
Design space
0.35 for t/c=0.07c
0.50 for t/c=0.10c

13. Result1 13
Convergence history of GA exploration
t007c-1
Best design in t007c-2
this generation t010c-1
t010c-2
Worst design in
this generation
t/c=0.07c t/c=0.10c
 Population size: 20
 15 generations for t/c=0.07c，11 generations for t/c=0.10c (in progress)
 In each case, solutions are almost converged. (Maximum l/d 45, and 38,
respectively.)
 Four promising solutions are picked up.

14. Result2 14
α vs. l/d
 t0.07c-1 and -2 achieve better performance than baseline.
 t0.10c-1/-2 achieve almost same maximum l/d, and better
performance at not design point.

15. Result3 15
α vs. Cl
 t0.07c-1, -2, t0.10c-1, and -2 achieve similar Cl-AoA.
 l/d is improved because of higher Cl.

16. Result4 16
α vs. Cd
 In t=0.07c design, drag was increased 5% compared with baseline.
 In t=0.10c design, drag was increased 10% compared with baseline.
 Drag minimization also have to be considered for next step.

17. Result5 17
Geometry and flowfield (t/c=0.07c)
t007c-1(AoA=2.9deg.) t007c-2(AoA=3.0deg.)
 Cp distributions when the airfoil achieves
maximum l/d obtained from t007c case
 Thickness distribution is similar to baseline.
 LE radiuses of t007c-1/-2 are smaller than
that of baseline.
 Cambers of t007c-1/-2 are larger than that
of baseline.
Baseline (AoA=4.0deg.)  Pressure recoveries on the upper surfaces
of t007c-1/-2 are relaxed.

18. Result6 18
Geometry and flowfield (t/c=0.07c)
t010c-1(AoA=3.2deg.) t010c-2(AoA=3.3deg.)
 Cp distributions when the airfoil achieves
maximum l/d obtained from t010c case.
 LE radiuses of t007c-1/-2 are smaller than
that of baseline.
 Cambers of t007c-1/-2 are larger than that
of baseline.
 Pressure recoveries on the upper surfaces
of t010c-1/-2 are also relatively relaxed.
Baseline (AoA=4.0deg.)

19. Result7
 Comparison of parameters among solutions and baseline
 Modified PARSEC represents Ishii like airfoil by parameter
identification.
t007c-1 t007c-2 t010c-1 t010c-2 Ishii like airfoil
dv1 LE radius (rle) 0.0040 0.0042 0.0042 0.0053 0.0086
x-coord. of maximum
・x coordinate (dv7) of maximum camber
dv2 thickness (xt)
0.2891 0.2891 0.3322 0.3333 0.2000
LE radius small
comes up to LE.
dv3
z-coord. of maximum
thickness (zt)
0.0350 0.0350 0.0500 0.0500 0.0350
・ LE camber (dv6), maximum camber,(dv8) -0.5837
dv4
curvature at maximum
thickness (zxxt )
-0.5275 -0.5276 -0.5841 -0.4600
and TE camber (dv11) tend to be large.
dv5 angle of TE (βte) 7.9650 7.9649 8.7658 8.7707 5.0000
dv6 camber radius at LE (rc) 0.0024 0.0024 0.0033 0.0023 0.0016
x-coord. of maximum camber
dv7 (xc)
0.3276 0.3244 0.3124 0.3123 0.5200
z-coord. of maximum camber
dv8 (zc)
0.0352 0.0332 0.0375 0.0379 0.0200
curvature at maximum camber
dv9 (zxxc)
-0.0269 -0.0212 -0.0049 -0.0077 -0.2500
dv10 z-coordinate of TE (zte) -0.0045 -0.0087 -0.0007 -0.0008 0.0000
dv11 angle of camber at TE (αte) 9.3007 9.1802 10.2644 11.2638 4.5000

20. Result8 20
Visualization of design problem (t/c=0.07c)
Baseline
l/d>43.0
All solutions obtained by GA
Pick up individuals which achieve better L/D than 43.0

21. Result8 21
Visualization of design problem (t/c=0.07c)
Baseline
l/d>43.0
To obtain better maximum l/d,
 Smaller LE radius (dv1), and curvature (dv4)
 Closer maximum camber position xc (dv7) to LE
 Larger angle of TE (dv5)
 Larger curvature maximum camber (dv9)
 Larger camber angle at TE (dv11)
 Almost same thickness at 25% chord and 75%
cord compared with baseline

22. Result9 22
Visualization of design problem (t/c=0.10c)
Baseline
l/d>4370
All solutions obtained by GA
Pick up individuals which achieve better L/D than 37.0

23. Result9 23
Visualization of design problem (t/c=0.07c)
l/d>37.0
To obtain better maximum l/d,
 Smaller LE radius (dv1), and curvature (dv4)
 Closer maximum camber position xc (dv7) to LE
 Larger angle of TE (dv5)
 Larger curvature maximum camber (dv9)
 Larger camber angle at TE (dv11)
 Almost same thickness at 25% chord and 75%
cord compared with baseline

24. Result10 24
Comparison between two cases (t/c=0.07c and t/c=0.10c)
t007c-1
Green: t/c=0.07
Purple: t/c=0.10
t010c-1
 Almost same design variables (except for thickness)
showed better objective function compared with two cases.

25. Conclusions 25
 Design exploration of airfoil for Mars-airplane
 Design optimization using CFD and GA
 Selections of promising designs and investigations of their
performances
 Improvement of maximum l/d in t/c=7% case
 Acquirements of airfoils which achieves relaxed pressure recovery on
the upper surface
 Higher Cl, but higher Cd than baseline
 Knowledge discovery by means of ANOVA and SPM to obtain better
maximum l/d
 Smaller LE radius, and uppersurface curvature
 Closer maximum camber position xc to LE
 Larger angle of TE
 Larger curvature maximum camber
 Larger camber angle at TE
Further study: Consideration of Cd minimization

26. Acknowledgement 26
We thank members of the Mars-airplane working
group in ISAS/JAXA for giving their experimental
data and their valuable advices.
Thank you very much for your kind attention.