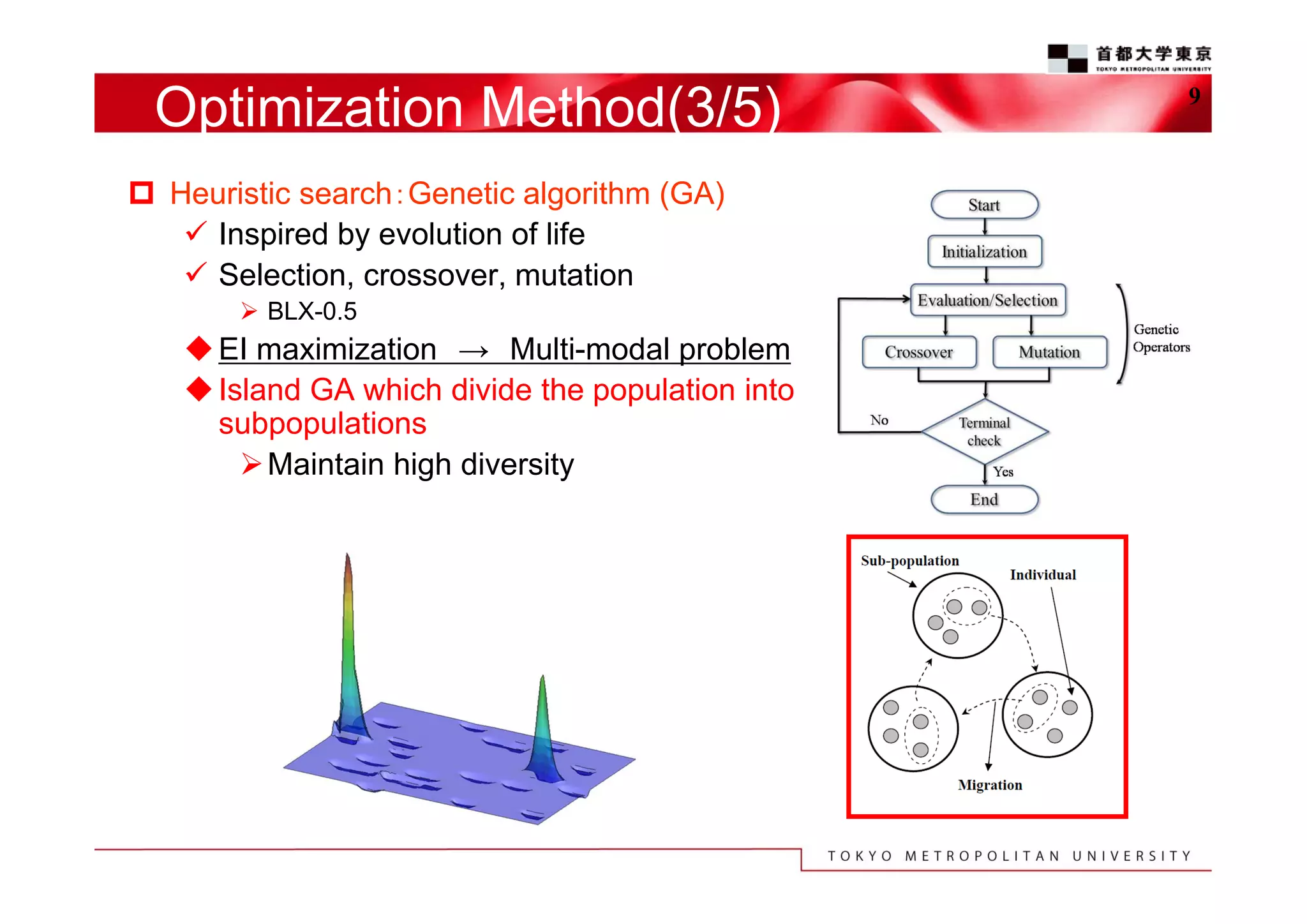
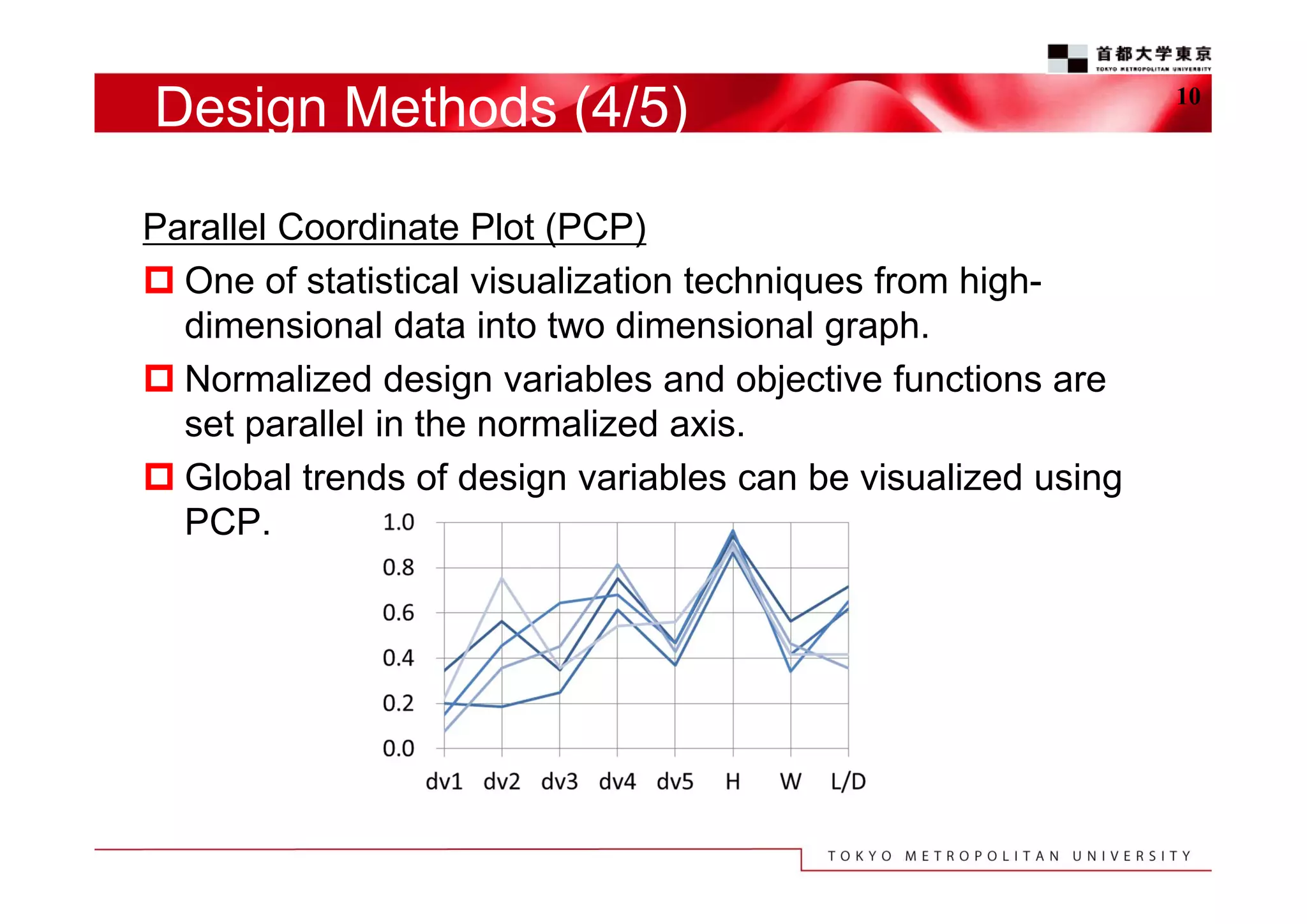
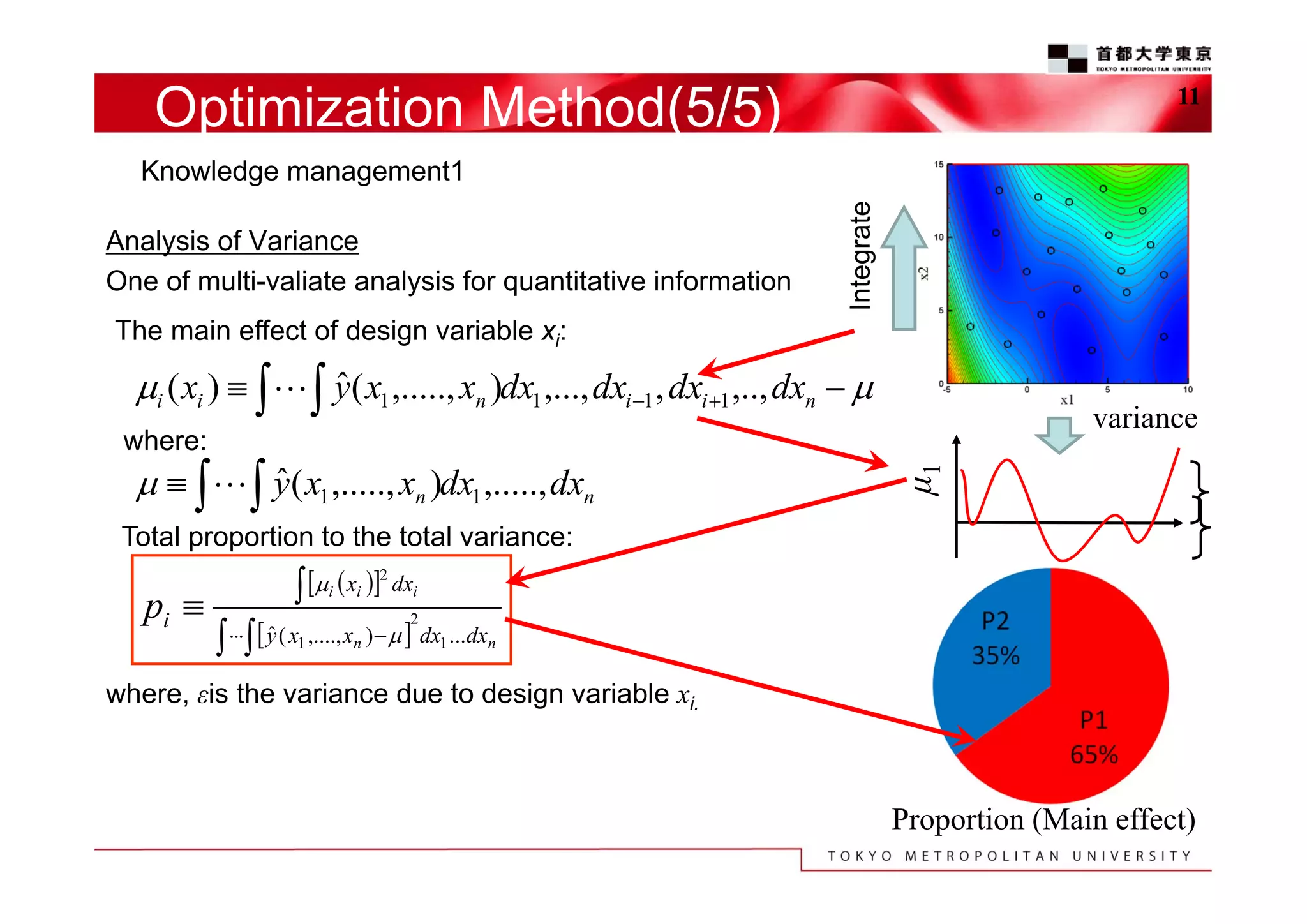
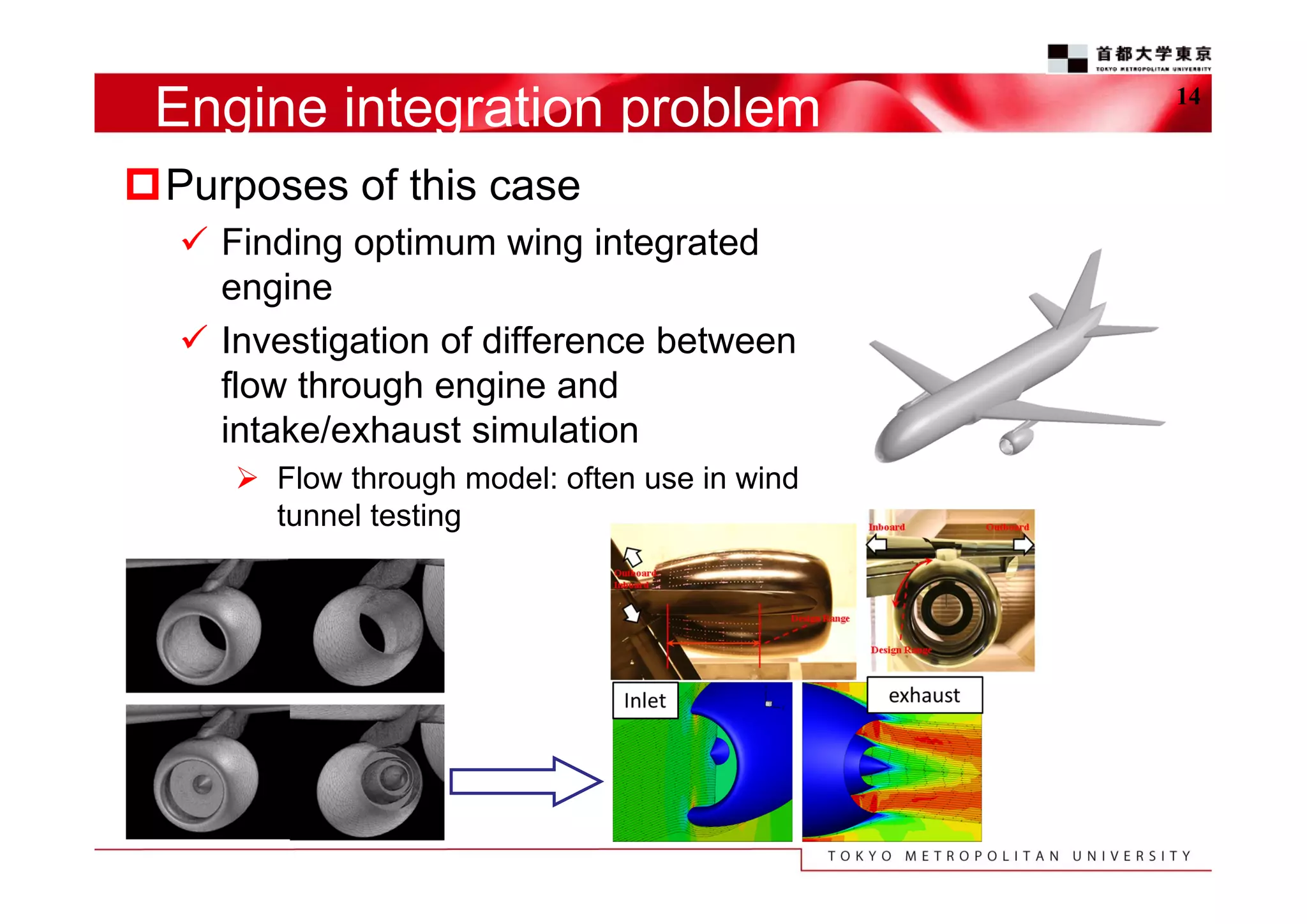
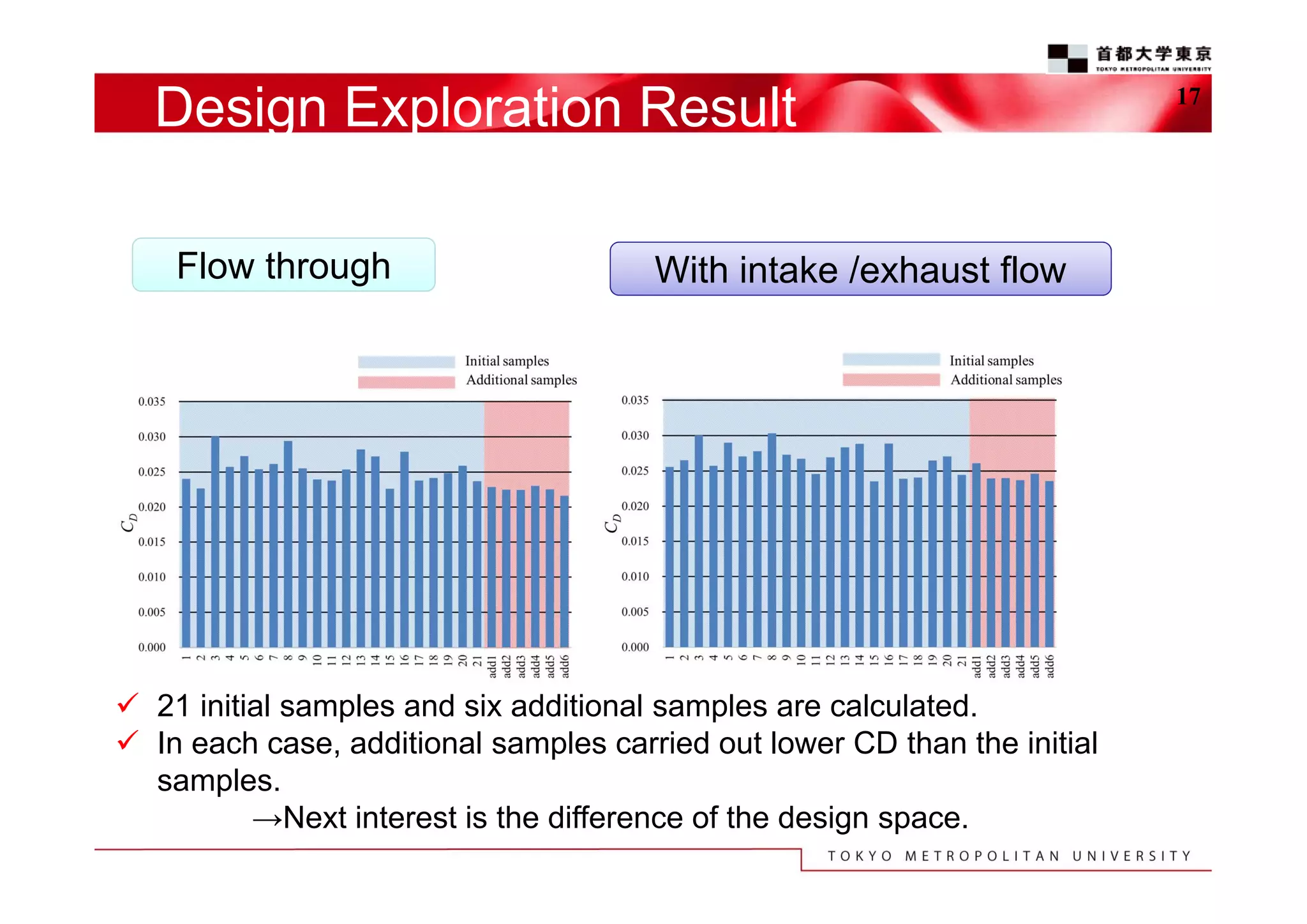
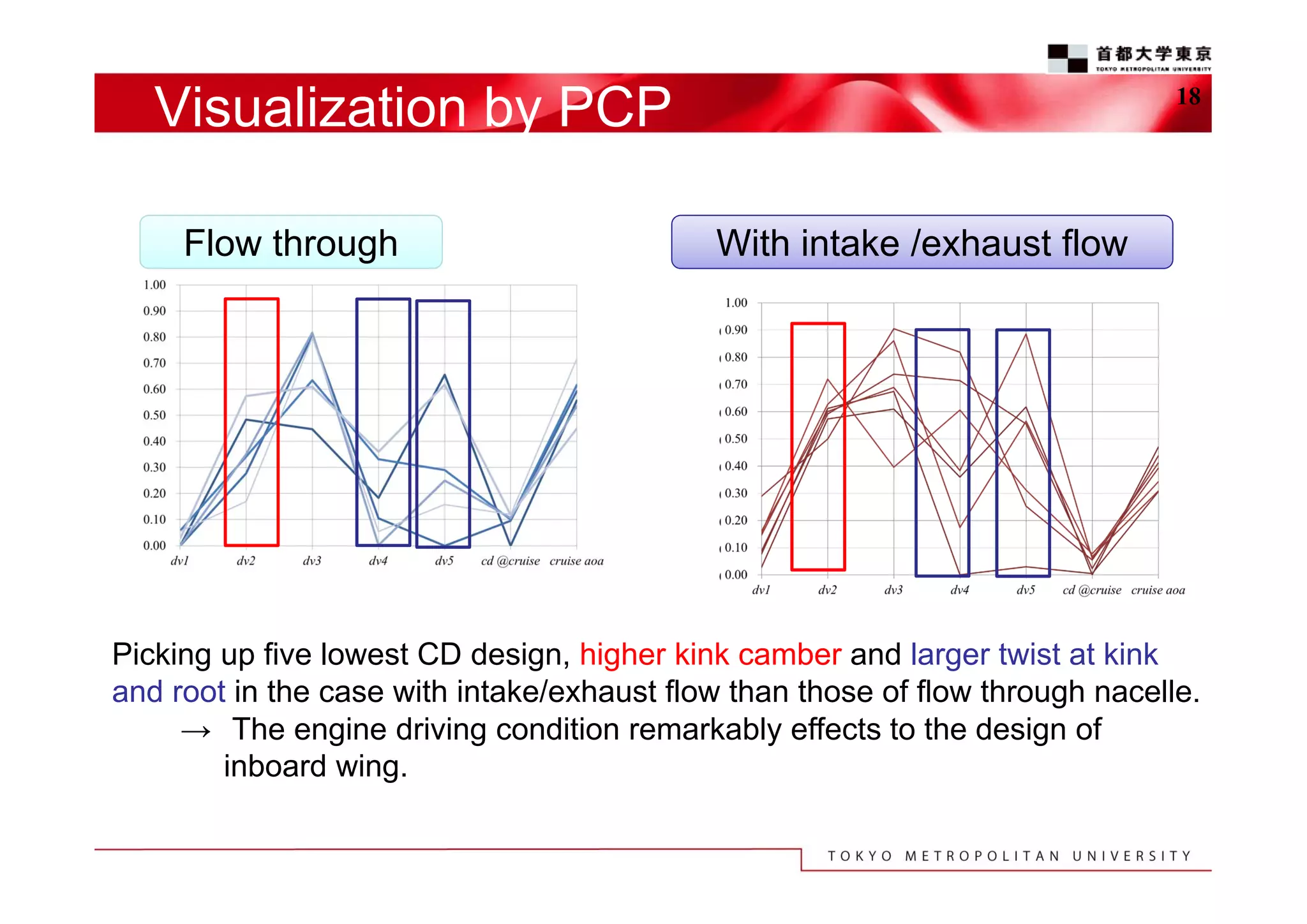
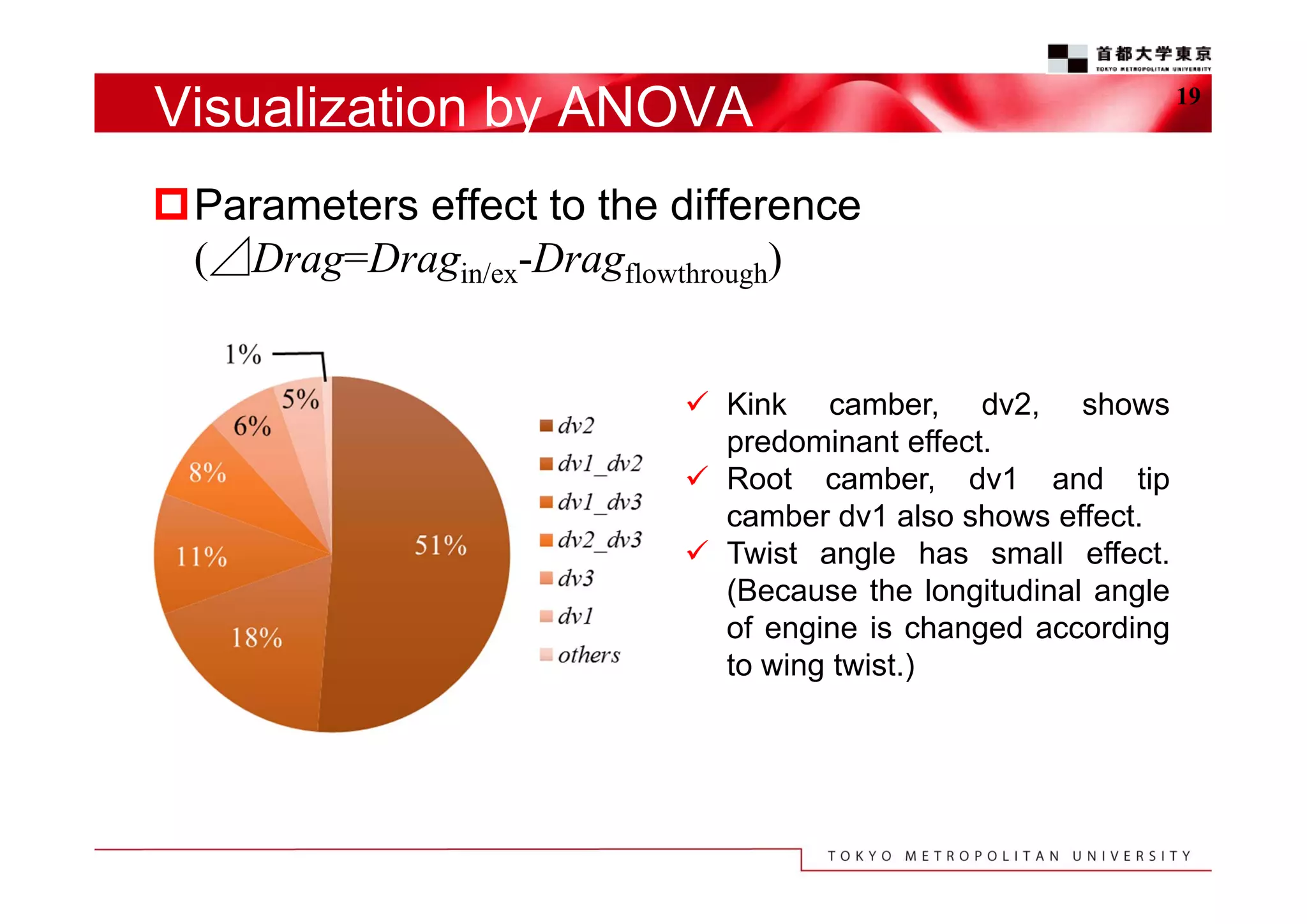
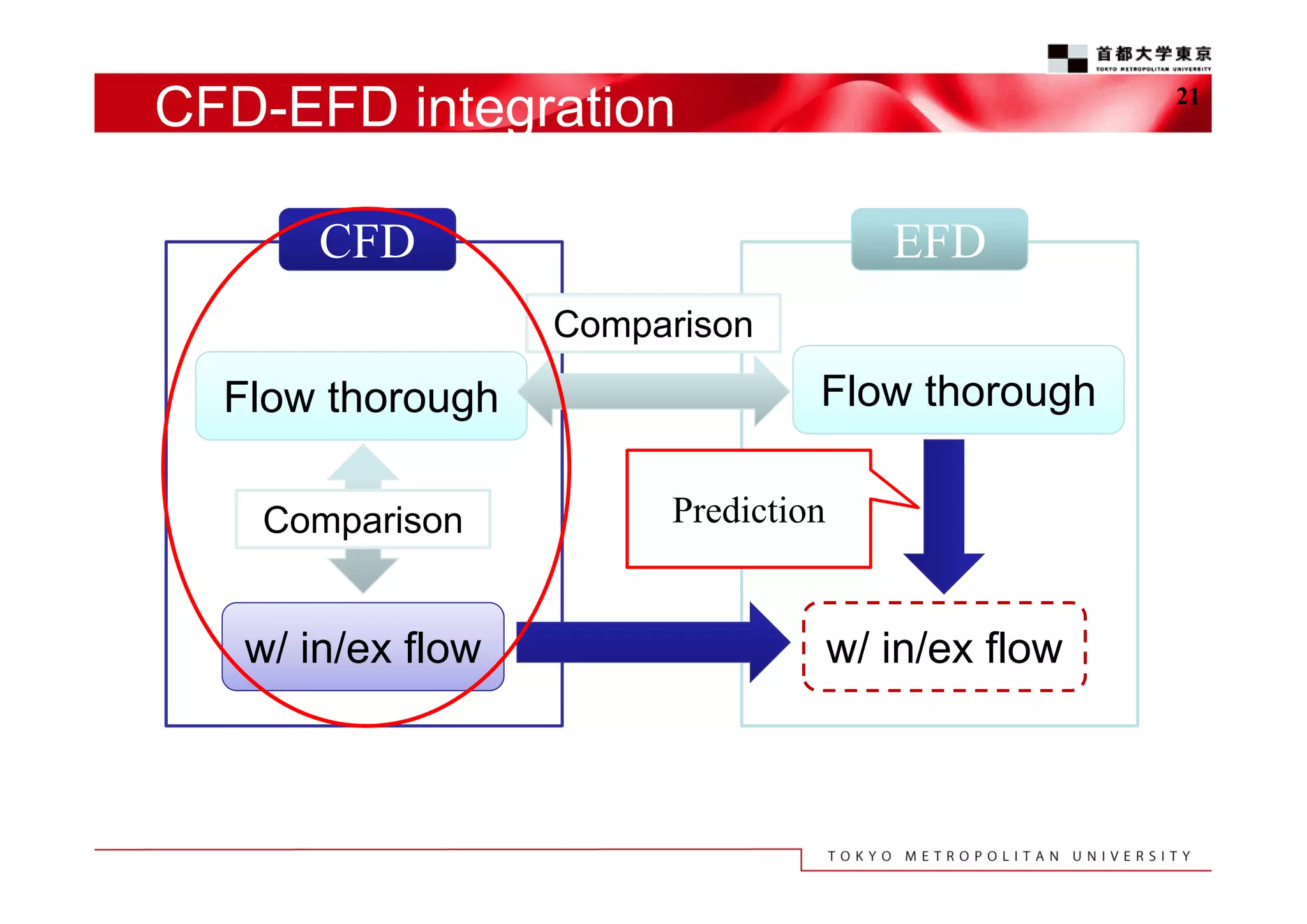
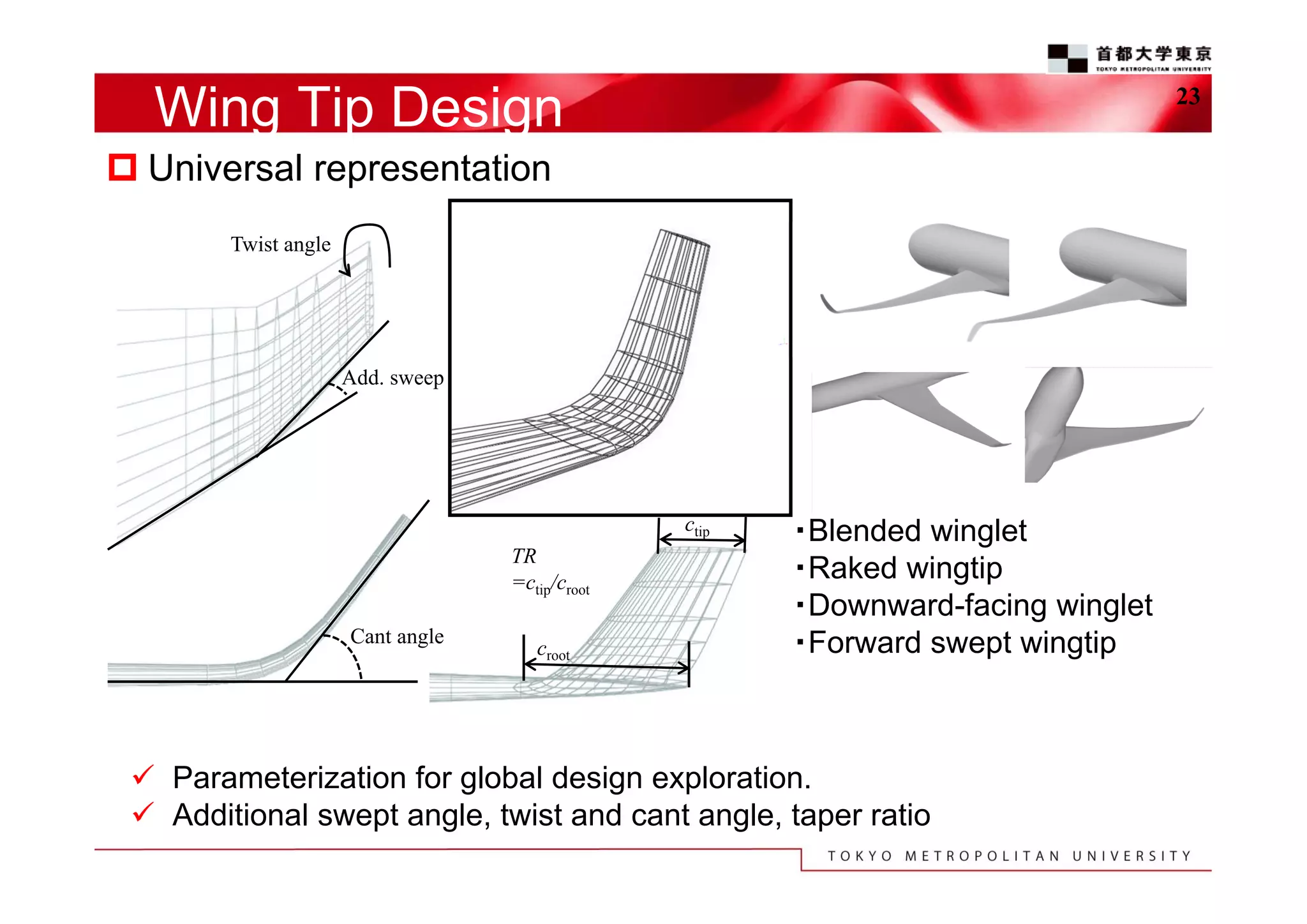
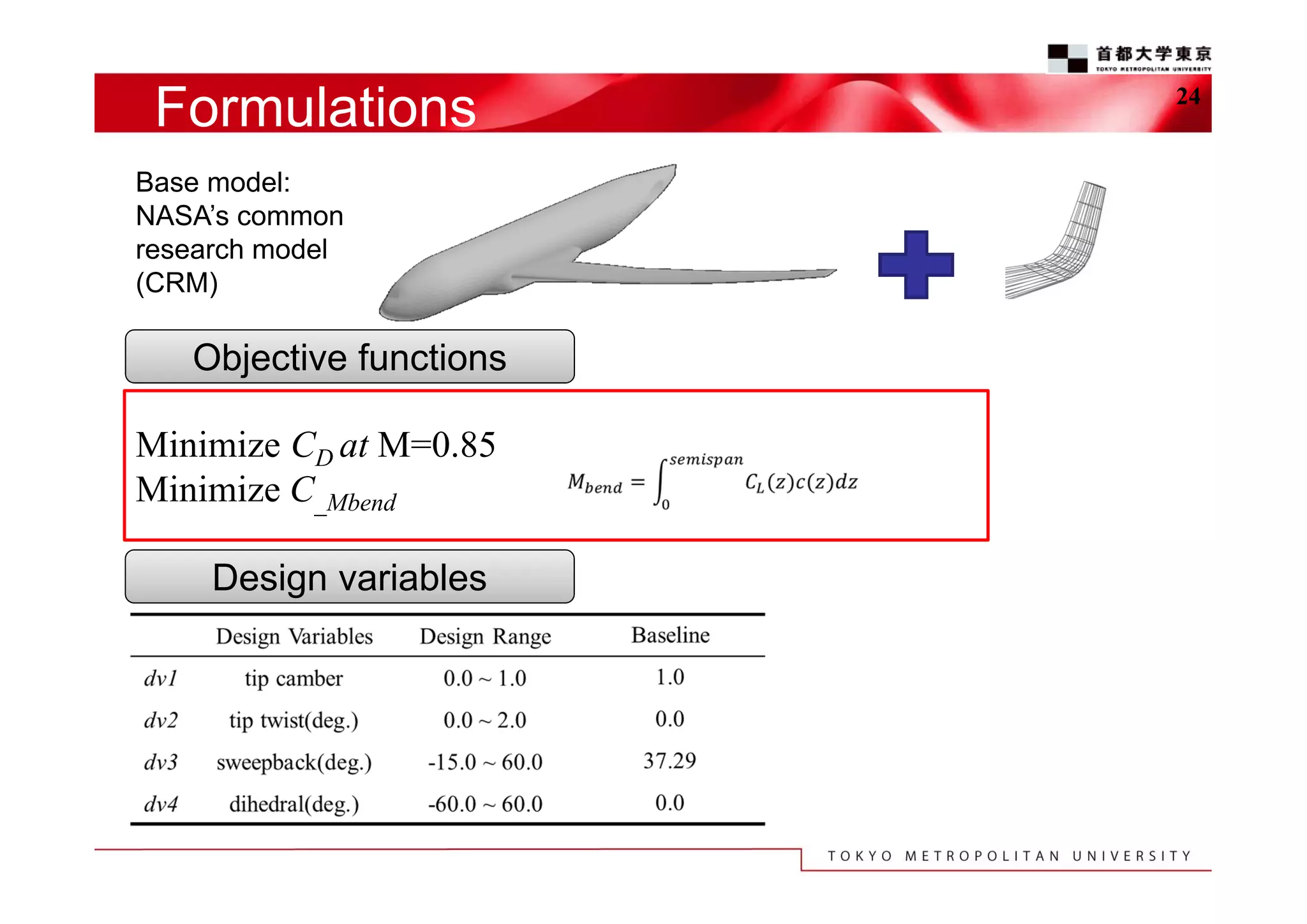
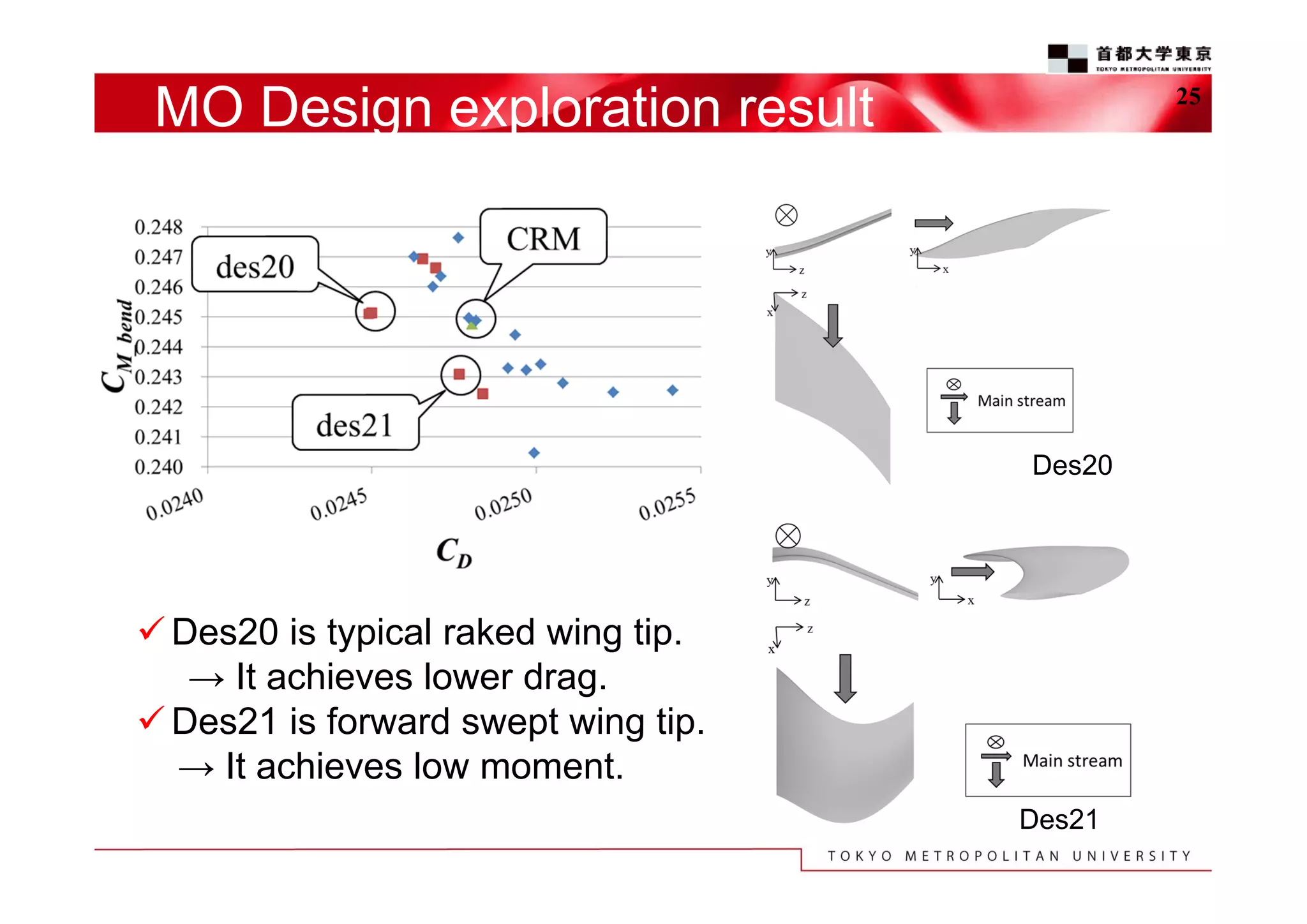
The document discusses the efficient design exploration for civil aircraft using a kriging-based genetic algorithm. It presents two case studies focused on optimizing the aerodynamic design of a wing integrated engine nacelle and multi-disciplinary design of wing tips, employing efficient global optimization methods. The findings emphasize the significance of design variables affecting drag and the importance of integrating knowledge discovery techniques for enhancing design processes.

1. Eurogen 2013
October 7–9, 2013, Las Palmas de Gran Canaria, Spain
Efficient Design Exploration for Civil Aircraft
Using a Kriging-Based Genetic Algorithm
Mashiro Kanazaki
Tokyo Metropolitan University

2. Contents
Introduction
Aerodynamic Design of Civil Transport
Optimization method
Efficient Global Optimization
Data mining
Flow solver
Case1: Optimization of wing integrated engine
nacelle
Case2: Multi-disciplinary design of wing tip
Conclusions
2

3. Introductino1
3
Aerodynamic Design of Civil Transport
 Design Considering Many Requirement




High fuel efficiency
Low emission
Low noise around airport
Conformability
 Computer Aided Development
 For higher aerodynamic performance
 For noise reduction
Time consuming computational
fluid dynamics (CFD)
Efficient and global optimization is desirable.

4. Introduction2
4
Cl
Efficient design
Many requirements for real world problem: cost, efficiency,
emission, noise..
Many constraint, such astarget lift, minimization of bending
and torsion moments → several evaluations for one case
(10-30hours)
target Cl
Cd
x
Genetic algorithm with surrogate model is realistic method
for aerodynamic design in aeronautical engineering

5. Introduction3
Several efficient and global optimization
Combination of heuristic optimization and
surrogate model
Efficient Global Optimization(Jones, D. R., 1998)
Analysis design problem using data mining
Multi-Objective Design Exploration (Obayashi, S. and
Jeong, S., 2005)
5

6. Objectives
Introduction of efficient global optimization with high
fidelity flow solver (such as Navier-Stokes solver)
Kriging model
Genetic Algorithm
Knowledge discovery using ANOVA and SOM
Application of realistic design problem
Wing design for an engine nacelle installed under
the wing (Case1)
Multi-disciplinary design of wing let (Case2)
6

7. Optimization Method(1/5)
7
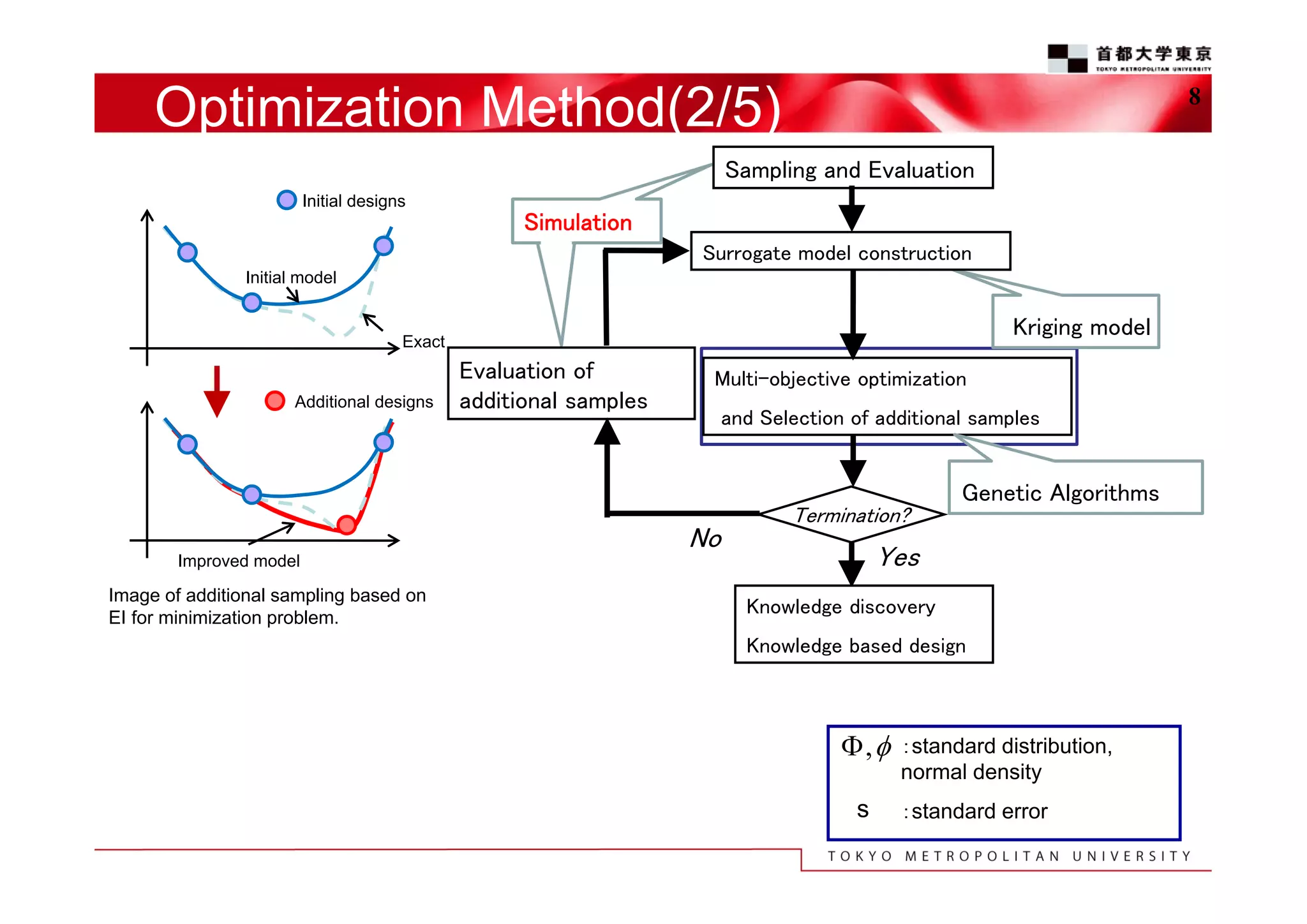
 Surrogate model：Kriging model
 Interpolation based on sampling data
 Standard error estimation (uncertainty)
y (xi )     (xi )
global model
localized deviation
from the global model
 EI(Expected Improvement)
 The balance between optimality and uncertainty
 EI maximum point has possibility to improve the model.
Improvement at a point x is
I=max(fmin-Y,0)
Expected improvement E[I(x))]=E[max(fmin-Y,0)]
To calculate EI,
Jones, D. R., “Efficient Global
Optimization of Expensive BlackBox Functions,” J. Glob. Opt., Vol.
13, pp.455-492 1998.

8. Optimization Method(2/5)
8
Sampling and Evaluation
Initial designs
Simulation
Surrogate model construction
Initial model
Kriging model
Exact
Additional designs
Improved model
Image of additional sampling based on
EI for minimization problem.
Evaluation of
additional samples
Multi-objective optimization
and Selection of additional samples
No
Termination?
Genetic Algorithms
Yes
Knowledge discovery
Knowledge based design
,
s
：standard distribution,
normal density
：standard error

9. Optimization Method(3/5)
 Heuristic search：Genetic algorithm (GA)
 Inspired by evolution of life
 Selection, crossover, mutation
 BLX-0.5
 EI maximization → Multi-modal problem
 Island GA which divide the population into
subpopulations
 Maintain high diversity
9

10. Design Methods (4/5)
Parallel Coordinate Plot (PCP)
 One of statistical visualization techniques from highdimensional data into two dimensional graph.
 Normalized design variables and objective functions are
set parallel in the normalized axis.
 Global trends of design variables can be visualized using
PCP.
10

11. Optimization Method(5/5)
11
Analysis of Variance
One of multi-valiate analysis for quantitative information
Integrate
Knowledge management1
The main effect of design variable xi:
ˆ
i ( xi )     y( x1 ,....., xn )dx1 ,..., dxi 1 , dxi 1 ,.., dxn  
variance
ˆ
     y( x1 ,....., xn )dx1 ,....., dxn
μ1
where:
Total proportion to the total variance:
pi 
 i  xi  dxi
2


ˆ
  y ( x1 ,...., xn )    dx1 ...dxn
2
where, εis the variance due to design variable xi.
Proportion (Main effect)

12. Aerodynamic evaluation
Navier-Stockes Solver for complex geometry
 Governing equation: Reynolds Averaged Navier-Stokes
solver
Turbulent model: Spalart-Allmaras model
Time integration: LU-SGS
Flux evaluation HLLEW
Computational Grid
 Tetra based Unstructured Grid
Total number of grid about 7 million.
12

13. 13
Case１
Wing design for an engine nacelle
installed under the wing

14. Engine integration problem
Purposes of this case
 Finding optimum wing integrated
engine
 Investigation of difference between
flow through engine and
intake/exhaust simulation
 Flow through model: often use in wind
tunnel testing
14

15. Evaluation of Boundary Condition
 Intake
 Neumann condition
according to the flow in
front of intake
 Exhaust
 Calculate by / 0 , / 0
,
0,
: total pressure and temperature at boundary.
0: total pressure and temperature of main stream.
15

16. Formulations
16
 Optimization for two cases
 With flow through engine
 With simulating of intake/exhaust flow
Objective functions
Minimize CD (Drag coefficient)
Subject to CL = 0.3
Design variables
Design Variables
Design range
dv1
Camber (Wing root)
0.00~1.00
dv2
Camber (Wing kink)
0.00~1.00
dv3
Camber (Wing tip)
0.00~1.00
dv4
Twist angle at kink
0.01~0.50
dv5
Twist angle at tip
0.50~2.00

17. Design Exploration Result
Flow through
With intake /exhaust flow
 21 initial samples and six additional samples are calculated.
 In each case, additional samples carried out lower CD than the initial
samples.
→Next interest is the difference of the design space.
17

18. Visualization by PCP
Flow through
18
With intake /exhaust flow
Picking up five lowest CD design, higher kink camber and larger twist at kink
and root in the case with intake/exhaust flow than those of flow through nacelle.
→ The engine driving condition remarkably effects to the design of
inboard wing.

19. Visualization by ANOVA
Parameters effect to the difference
(⊿Drag=Dragin/ex-Dragflowthrough)
 Kink camber, dv2, shows
predominant effect.
 Root camber, dv1 and tip
camber dv1 also shows effect.
 Twist angle has small effect.
(Because the longitudinal angle
of engine is changed according
to wing twist.)
19

20. CFD-EFD integration
These knowledge will be useful for
simulation/experiment integration.
DAHWIN system developed in JAXA
Visit: http://integration2012.jaxa.jp/
http://www.aero.jaxa.jp/eng/
20

21. CFD-EFD integration
21
CFD
EFD
Comparison
Flow thorough
Comparison
w/ in/ex flow
Flow thorough
Prediction
w/ in/ex flow

22. 22
Case2
Wing tip design considering the
bending moment

23. Wing Tip Design
23
 Universal representation
Twist angle
Add. sweep
ctip
TR
=ctip/croot
Cant angle
croot
・Blended winglet
・Raked wingtip
・Downward-facing winglet
・Forward swept wingtip
 Parameterization for global design exploration.
 Additional swept angle, twist and cant angle, taper ratio

24. Formulations
Base model:
NASA’s common
research model
(CRM)
Objective functions
Minimize CD at M=0.85
Minimize C_Mbend
Design variables
24

25. MO Design exploration result
25
Des20
 Des20 is typical raked wing tip.
→ It achieves lower drag.
 Des21 is forward swept wing tip.
→ It achieves low moment.
Des21

26. Flow visualizations M=0.85
26
 Impact of swept angle to flowfield
 Smaller vortex with raked wing tip (Des20)
 Diffused vortex with forward swept wing tip (Des21)
des1
des20
des21

27. Conclusions
 High-efficient design procedure for aerodynamic design.
 Employment of EGO’s efficient global search
 Genetic algorithm, and Kriging surrogate model
 Knowledge discovery techniques, such as ANOVA and PCP
 Design knowledge management
 Two cases could successfully solved.
 Effect of the difference to the wing design due engine
driving condition
 Multi-disciprinaly design of wing tip.
27