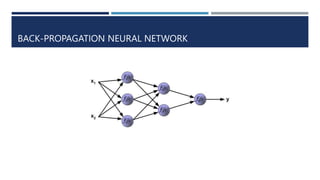
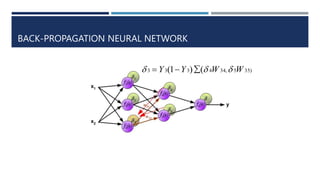
The document discusses agent adaptability, defining an adaptive agent as one that can respond to stimuli in its environment. It differentiates between simple reactive agents and more advanced reasoning and learning agents, outlining techniques like genetic algorithms, reinforcement learning, and back-propagation in neural networks. Additionally, it covers methods of clustering, including k-means and DBSCAN, in the context of adaptable agent technologies.

1. AGENT ADAPTABILITY
ASMA KANWAL
LECTURER
GC UNIVERSITY, LAHORE

2. AGENT ADAPTABILITY
 An agent is considered adaptive if it is capable of responding to other agents and/or its environment to
some degree. At a minimum, this means that an agent must be able to react to a simple stimulus to
make a direct, predetermined response to a particular event or environmental signal. Thermostats,
robotic sensors, and simple search bots fall into this category.
 Beyond the simple reactive agent is the agent that can reason. Reasoning agents react by making
inferences and include patient diagnosis agents and certain kinds of data-mining agents.
 More advanced forms of adaptation include the capacity to learn and evolve. These agents can change
their behavior based on experience. Common software techniques for learning are neural networks,
Bayesian rules, credit assignments, and classifier rules. Examples of learning agents would be agents that
can approve credit applications, analyze speech, and recognize and track targets.
 A primary technique for agent evolution usually involves genetic algorithms and genetic programming.

3. TECHNIQUES FOR ADAPTABILITY
 Reinforcement Learning
 Clustering
 Rote Learning
 Version Spaces
 Grammatical Inference

4. BIOLOGICAL NEURON STRUCTURE

5. PERCEPTRON LAW
Working of single neuron consist on four steps
Step-1: Net Calculation  𝑛𝑒𝑡𝑓(𝑒) = 𝑥1 ∗ 𝑤1 + 𝑥2 ∗ 𝑤2
Step-2: Output Calculation  𝑦𝑓 𝑒 = 𝑖𝑓 𝑛𝑒𝑡𝑓(𝑒) > θ 𝑡ℎ𝑒𝑛 𝑦𝑓 𝑒 = 1 𝑒𝑙𝑠𝑒 𝑦𝑓(𝑒) = 0
Step-3: Error Calculation  δ𝑓(𝑒) = 𝑡𝑎𝑟𝑔𝑒𝑡 − 𝑦𝑓(𝑒)
Step-4: Weight Update 𝑤1
𝑛𝑒𝑤
= 𝑤1
𝑜𝑙𝑑
+ δ𝑓(𝑒) ∗ α ∗ 𝑥1
Key Steps:
Weights assignment
Learning Rate
Threshold
Biased error

6. THRESHOLD FUNCTIONS [TRANSFER FUNCTION]

7. STRUCTURE OF NEURAL NETWORK
 Layers
 Input Layer [based on input features]
 Hidden Layers
 Output Layer [based on output]
Learning Rate

8. BACK-PROPAGATION NEURAL NETWORK

9. SUB-STEP OF BACKPROPAGATION

10. BACK-PROPAGATION NEURAL NETWORK

11. BACK-PROPAGATION NEURAL NETWORK
𝑦1 = 𝑁𝑒𝑡1 > θ 𝑡ℎ𝑒𝑛 𝑦1 = 1 𝑒𝑙𝑠𝑒 𝑦1 = 0
Net 1

12. BACK-PROPAGATION NEURAL NETWORK
𝑦2 = 𝑁𝑒𝑡2 > θ 𝑡ℎ𝑒𝑛 𝑦2 = 1 𝑒𝑙𝑠𝑒 𝑦2 = 0
Net 2

13. BACK-PROPAGATION NEURAL NETWORK
𝑦3 = 𝑁𝑒𝑡3 > θ 𝑡ℎ𝑒𝑛 𝑦3 = 1 𝑒𝑙𝑠𝑒 𝑦3 = 0
Net 3

14. BACK-PROPAGATION NEURAL NETWORK
𝑦4 =
1
1 + 𝑒−𝑛𝑒𝑡(𝜆)
Net 4

15. BACK-PROPAGATION NEURAL NETWORK
𝑦5 =
1
1 + 𝑒−𝑛𝑒𝑡(𝜆)
Net 5

16. BACK-PROPAGATION NEURAL NETWORK
𝑦6 =
1
1 + 𝑒−𝑛𝑒𝑡(𝜆)
Net 6

17. BACK-PROPAGATION NEURAL NETWORK
δ6 = Y6 (1 - Y6)(t- Y6)
t
Y

18. BACK-PROPAGATION NEURAL NETWORK
46
6
4
4
4 )
1
( W
Y
Y 
 



19. BACK-PROPAGATION NEURAL NETWORK
56
6
5
5
5 )
1
( W
Y
Y 
 



20. BACK-PROPAGATION NEURAL NETWORK
)
15
5
,
14
4
1
1
1 (
)
1
( W
W
Y
Y 

 



21. BACK-PROPAGATION NEURAL NETWORK
)
25
5
,
24
4
2
2
2 (
)
1
( W
W
Y
Y 

 



22. BACK-PROPAGATION NEURAL NETWORK
)
35
5
,
34
4
3
3
3 (
)
1
( W
W
Y
Y 

 



23. BACK-PROPAGATION NEURAL NETWORK

24. BACK-PROPAGATION NEURAL NETWORK
weight = weight + learning_rate * error * input

25. BACK-PROPAGATION NEURAL NETWORK

26. BACK-PROPAGATION NEURAL NETWORK

27. BACK-PROPAGATION NEURAL NETWORK

28. BACK-PROPAGATION NEURAL NETWORK

29. REINFORCEMENT LEARNING ANN

30. CLUSTERING
 K-mean Clustering
 DBScan
 Expectation Maximization
 Agglomerative Hierarchical Clustering

31. DBSCAN (DENSITY BASED SPATIAL CLUSTERING APPLICATION WITH
NOISE)