This document presents a novel adaptive sliding-mode control system to control the speed of an induction motor drive. The control system uses vector (field-oriented) control theory for induction motor drives and incorporates an adaptive sliding-mode control law. This adaptive law calculates the sliding gain online without needing to determine an upper bound on system uncertainties. Simulation results show the proposed controller provides high performance, is robust to parameter variations and external load disturbances, and reduces chattering compared to traditional sliding-mode controllers.

1. Journal oftheFranklinInstitute348(2011)300–314
A robustvectorcontrolforinductionmotordrives
with anadaptivesliding-modecontrollaw
Oscar Barambonesa,, PatxiAlkortab
aDpto. Ingenier´ıa deSistemasyAutom atica, EUIdeVitoria,UniversidaddelPa´ıs Vasco,Nievescano12,01006
Vitoria, Spain
bDpto. Ingenier´ıa deSistemasyAutom atica, EUIdeEibar,UniversidaddelPa´ıs Vasco,Avda.Otaola,2920600
Eibar (Gipuzkoa)
Received 4January2010;receivedinrevisedform24November2010;accepted30November2010
Available online7December2010
Abstract
A noveladaptivesliding-modecontrolsystemisproposedinordertocontrolthespeedofan
induction motordrive.Thisdesignemploystheso-calledvector(orfieldoriented)controltheoryfor
the inductionmotordrives.Thesliding-modecontrolisinsensitivetouncertaintiesandpresentsan
adaptive switchinggaintorelaxtherequirementfortheboundoftheseuncertainties.Theswitching
gain isadaptedusingasimplealgorithmwhichdoesnotimplyahighcomputationalload.Stability
analysis basedonLyapunovtheoryisalsoperformedinordertoguaranteetheclosedloopstability.
Finally, simulationresultsshownotonlythattheproposedcontrollerprovideshigh-performance
dynamic characteristics,butalsothatthisschemeisrobustwithrespecttoplantparametervariations
and externalloaddisturbances.
2010 TheFranklinInstitute.PublishedbyElsevierLtd.Allrightsreserved.
1. Introduction
The inductionmotorisacomplexstructurethatconvertselectricalenergy intomechanical
energy. Althoughinductionmachineswereintroducedmorethanahundredyearsago,the
researchanddevelopmentinthisareaappearsto benever-ending.Traditionally,ACmachines
with aconstantfrequencysinusoidalpower supplyhavebeenusedinconstant-speed
applications, whereasDC machineswerepreferredforvariablespeeddrives,sincetheypresent
www.elsevier.com/locate/jfranklin
0016-0032/$32.00 2010 TheFranklinInstitute.PublishedbyElsevierLtd.Allrightsreserved.
doi:10.1016/j.jfranklin.2010.11.008
Correspondingauthor.Tel.: þ34 945013235;fax: þ34 945013270.
E-mail address: ispbacao@ehu.es(O.Barambones).

2. a simplercontrol.Besides,ACmachinespresentedsomedisadvantagesincomparisonwith
DC ones,ashighercost,higherrotorinertiaand maintenanceproblems.Nevertheless,inthe
last twoorthreedecadeswehaveseenextensiveresearchanddevelopmenteffortsinvariable-
frequency,variable-speedAC machinedrivestechnology [1], whichhaveovercomesomeofthe
abovedisadvantagesoftheACmotors.
The developmentoffieldorientedcontrolinthebeginningof1970smadeitfeasibleto
control theinductionmotorasaseparatelyexcitedDCmotor [1–3]. Inthissense,thefield-
orientedtechniqueguaranteesthedecouplingoftorqueandfluxcontrolcommandsforthe
inductionmotor.Thismeansthatwhenthefluxisgovernedbymeansofcontrollingthe
current id, thetorqueisnotaffected.Similarly,whenthetorqueisgovernedbycontrolling
the current iq, thefluxisnotaffectedand,therefore,itcanbeachievedtransientresponse
as fastasinthecaseofDCmachines.
On theotherhand,whendealingwithindirectfield-orientedcontrolofinduction
motors,aknowledgeofrotorspeedisrequiredinordertoorienttheinjectedstatorcurrent
vector andtoestablishanadequatespeedfeedbackcontrol.Althoughtheuseofaflux
estimatorindirectfieldorientedcontroleliminatestheneedofthespeedsensorinorderto
orient theinjectedstatorcurrentvector,thismethodisnotpractical.Thisisbecausethe
flux estimatordoesnotworkproperlyinalowspeedregion.Thefluxestimatorpresentsa
pole ontheoriginofthe S plane (pureintegrator),andthereforeitisverysensitivetothe
offset ofthevoltagesensorandtheparametervariations.
However,thespeedorpositionsensorofinductionmotorstilllimitsitsapplicationsto
somespecialenvironmentsnotonlyduetothedifficultiesofmountingthesensor,butalso
becauseoftheneedoflowcostandreliablesystems.Theresearchanddevelopmentworkon
a sensorlessdriverfortheACmotorisprogressinggreatly.Muchworkhasbeendoneusing
thefieldorientedbasedmethodapproach [4–7]. Intheseschemesthespeedisobtainedbased
onthemeasurementofstatorvoltagesandcurrents.Ontheotherhand,theinductionmotor
modelcanbeobtainedusingaNeuralNetworkapproach.IntheworkofAlanisetal. [8]
a discrete-timenonlinearsystemidentificationviarecurrenthighorderneuralnetworksis
proposed.Inthisworkasixth-orderdiscrete-timeinductionmotormodelinthestatorfixed
referenceframeiscalculatedusingtheproposedrecurrentneuralnetworksscheme.
Nevertheless,therobustnesstoparametervariationsandloaddisturbancesinthe
inductionmachinesstilldeservestobefurtherstudiedand,inparticular,specialattention
should bepaidtothelowspeedregiontransients.
Thus, theperformanceofthefieldorientedcontrolstronglydependsonuncertainties,
which areusuallyduetounknownparameters,parametervariations,externalload
disturbances,unmodelledandnonlineardynamics,etc.Therefore,manystudieshavebeen
made onthemotordrivesinordertopreservetheperformanceundertheseparameter
variationsandexternalloaddisturbances,suchasnonlinearcontrol,optimalcontrol,
variablestructuresystemcontrol,adaptivecontrol,neuralcontrolandfuzzycontrol
[9–13]. Recently,thegeneticalgorithmapproachhasalsobeenusedinordertocontrolthe
electric motors.TheworkofMontazeri-Ghetal. [14], describestheapplicationofthe
geneticalgorithmfortheoptimizationofthecontrolparametersinparallelhybridelectric
vehiclesdrivenbyanelectricinductionmachine.
To overcometheabovesystemuncertainties,the variablestructurecontrolstrategyusing
the sliding-modehasbeenfocussedonmanystudiesandresearchforthecontroloftheAC
servo drivesysteminthepastdecade [15–19]. Thesliding-modecontrolcanoffermanygood
properties,suchasgoodperformanceagainstunmodelled dynamics,insensitivitytoparameter
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 301

3. variations,externaldisturbance rejection andfastdynamicresponse [20]. Theseadvantagesof
the sliding-modecontrolmaybeemployedinthepositionandspeedcontrolofanACservo
system.
The robustpropertiesofthesliding-modesystemsarealsobeenemployedinthe
observersdesign [21]. Inthisworkanobserver-basedsliding-modecontrolproblemis
investigatedforaclassofuncertaindeltaoperatorsystemswithnonlinearexogenous
disturbanceandthecontrolsystemstabilityisdemonstratedusingtheLyapunovstability
theory. IntheworkofBoiko [22] the estimationprecisionandbandwidthofsliding-mode
observersareanalyzedinthefrequencydomainfordifferentsettingsoftheobserverdesign
parameters.Inthispaperanexampleofsliding-modeobserverdesignforestimationofDC
motor speedfromthemeasurementsofarmaturecurrentisconsidered.
A position-and-velocitysensorlesscontrolforbrushlessDCmotorsusinganadaptive
sliding modeobserverisproposedinFuruhashi [23]. Inthisworkasliding-modeobserver
is proposedinordertoestimatethepositionandvelocityforbrushlessDCmotors.Then,
the velocityofthesystemisregulatedusingaPIcontrol.Asensorlesssliding-modetorque
control forinductionmotorsusedinhybridelectricvehicleapplicationsisdevelopedin
Proca etal. [24]. Thesliding-modecontrolproposedinthisworkallowsforfastandprecise
torque trackingoverawiderangeofspeed.Thepaperalsopresentstheidentificationand
parameterestimationofaninductionmotormodelwithvaryingparameters.Inthepaper
[25] a surveyofapplicationsofsecond-ordersliding-modecontroltomechanicalsystemsis
presented.Inthispaperdifferentsecond-ordersliding-modecontrollers,previously
presentedintheliterature,areshownandsomechallengingcontrolproblemsinvolving
mechanicalsystemsareaddressedandsolved.Arobustsliding-modesensorlessspeed-
control schemeofavoltage-fedinductionmotorisproposedinRashedetal. [26]. Inthis
work asecond-orderslidingmodeisproposedinordertoreducethechatteringproblem
that usuallyappearsinthetraditionalsliding-modecontrollers.IntheworkofAuroraand
Ferrara [27] a sliding-modecontrolalgorithmforcurrent-fedinductionmotorsis
presented.Inthispaperisproposedanadaptivesecond-ordersliding-modeobserverfor
speed androtorflux,andtheloadtorqueandtherotortimeconstantarealsoestimated.
Thehigherorderslidingmode(HOSM)proposedinthiswork,presentsomeadvantagesover
standardsliding-modecontrolschemes,oneofthemostimportantisthechatteringreduction.
However intheHOSManaccurateknowledgeofrotorfluxandmachineparametersisthekey
factorinordertoobtainahigh-performanceandhigh-efficiencyinduction-motorcontrol
scheme. Then,thesecontrolschemesrequireamorepreciseknowledgeofthesystemparameters
or theuseofestimatorsinordertocalculatethesystemparameters,whichimpliesmore
computationalcostthantraditionalsliding-modecontrollers.
On theotherhand,theslidingcontrolschemesrequirepriorknowledgeoftheupperbound
for thesystemuncertaintiessincethisboundis employed intheswitchinggaincalculation.
It shouldbenotedthatthechoiceofsuchboundmaynotbeeasilyobtainedduetothe
complicatedstructureoftheuncertainties inpracticalcontrolsystems [28,29]. Moreover,this
upperboundshouldbedeterminedasaccurately aspossible,becausethevaluetobe
considered fortheslidinggainincreaseswiththe bound,andthereforethecontroleffortwillbe
also proportionaltothisbound.Hence,ahigh upperboundforthesystemuncertainties
implies morecontroleffortandtheproblemofthechatteringwillbeincreased.
In ordertosurmountthisdrawback,inthispaperisproposedanadaptivelawinorder
to calculatetheslidinggain.Therefore,inourproposedadaptivesliding-modecontrol
scheme wedonotneedtocalculateanupperboundofthesystemuncertainties,which
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 302

4. greatlysimplifiesthecontrollerdesign.Moreover,thisupperboundcanbeunknownand
can bevariablealongthetimebecausetheslidinggainisadaptedon-line.
In thissense,thispaperpresentsanewsensorlessvectorcontrolschemeconsistingon
the onehandofaspeedestimationalgorithmsothatthereisnoneedforaspeedsensor
and ontheotherhandofanadaptativevariablestructurecontrollawwithanintegral
sliding surfacethatcompensatesfortheuncertaintiesinthesystem.Intheproposed
adaptivesliding-modecontrolscheme,unlikethetraditionalsliding-modecontrolschemes,
the slidinggainisnotcalculatedinadvance,becauseitisestimatedon-lineinorderto
compensatethepresentsystemuncertaintiesthatcanbevariablesalongthetime.
Using thisvariablestructurecontrolintheinductionmotordrive,thecontrolledspeedis
insensitivetovariationsinthemotorparametersandloaddisturbances.Thisvariable
structurecontrolprovidesagoodtransientresponseandexponentialconvergenceofthe
speed trajectorytrackingdespiteparameteruncertaintiesandloadtorquedisturbances.
The closedloopstabilityoftheproposedschemeisdemonstratedusingLyapunov
stabilitytheory,andtheexponentialconvergenceofthecontrolledspeedisalsoprovided.
Thisreportisorganizedasfollows.Therotor speedestimationisintroducedinSection2.
Then, theproposedrobustspeedcontrolwithadaptativeslidinggainispresentedinSection3.
In Section4,somesimulationresultsarepresented.Finally,concludingremarksarestatedin
the lastsection.
2. Rotorspeedcomputation
Many schemesbasedonsimplifiedmotormodelshavebeendevisedtosensethespeedof
the inductionmotorfrommeasuredterminalquantitiesforcontrolpurposes.Inorderto
obtain anaccuratedynamicrepresentationofthemotorspeed,itisnecessarytobasethe
calculationonthecoupledcircuitequationsofthemotor.
Since themotorvoltagesandcurrentsaremeasuredinastationaryframeofreference,it
is alsoconvenienttoexpresstheseequationsinthatstationaryframe.
From thestatorvoltageequationsinthestationaryframeitisobtained [3]:
_c
dr ¼
Lr
Lm
vds
Lr
Lm
Rs þ sLs
d
dt
ids ð1Þ
_c
qr ¼
Lr
Lm
vqs
Lr
Lm
Rs þ sLs
d
dt
iqs ð2Þ
where c is thefluxlinkage; L is theinductance; v is thevoltage; R is theresistance; i is the
current and s ¼ 1L2
m=ðLrLsÞ is themotorleakagecoefficient.Thesubscripts r and s
denoterespectivelytherotorandstatorvaluesreferredtothestator,andthesubscripts d
and q denote the dq-axiscomponentsinthestationaryreferenceframe.
The rotorfluxequationsinthestationaryframeare [3]
_c
dr ¼
Lm
Tr
idswrcqr
1
Tr
cdr ð3Þ
_c
qr ¼
Lm
Tr
iqs þ wrcdr
1
Tr
cqr ð4Þ
where wr is therotorelectricalspeedand Tr=Lr/Rr is therotortimeconstant.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 303

5. The angle ye of therotorfluxvector(cr ) inrelationtothe d-axisofthestationaryframe
is definedasfollows:
ye ¼ arctan
cqr
cdr
ð5Þ
being itsderivative:
_y
e ¼ we ¼
cdr
_c
qrcqr
_c
dr
c2
dr þ c2
qr
ð6Þ
SubstitutingEqs.(3)and(4)inEq.(6)itisobtained:
we ¼ wr
Lm
Tr
cdriqscqrids
c2
dr þ c2
qr
!
ð7Þ
Then, substitutingEq.(6)inEq.(7),andsolvingfor wr we obtain
wr ¼
1
c2
r
cdr
_c
qrcqr
_c
dr
Lm
Tr
ðcdriqscqridsÞ
ð8Þ
where c2
r ¼ c2
dr þ c2
qr.
Therefore,givenacompleteknowledgeofthemotorparameters,theinstantaneous
speed wr can becalculatedfromthepreviousequation,wherethestatormeasuredcurrent
and voltages,andtherotorfluxestimationobtainedfromarotorfluxobserverbasedon
Eqs. (1)and(2)havebeenemployed.
3. Variablestructurerobustspeedcontrolwithadaptiveslidinggain
In general,themechanicalequationofaninductionmotorcanbewrittenas
Jw_ m þ Bwm þ TL ¼ Te ð9Þ
where J and B are theinertiaconstantandtheviscousfrictioncoefficientoftheinduction
motorsystemrespectively; TL is theexternalload; wm is therotormechanicalspeedin
angularfrequency,whichisrelatedtotherotorelectricalspeedby wm=2wr/p where p is the
polenumbers,and Te denotesthegeneratedtorqueofaninductionmotor,definedas [3]
Te ¼
3p
4
Lm
Lr
ðce
drie
qsce
qrie
dsÞ ð10Þ
where ce
dr and ce
qr are therotor-fluxlinkages,thesubscript‘e’denotesthatthequantityis
referredtothesynchronouslyrotatingreferenceframe; iqs
e and ids
e are thestatorcurrents,
and p is thepolenumber.
The relationbetweenthesynchronouslyrotatingreferenceframeandthestationary
reference frameiscomputedbytheso-calledreversePark’stransformation:
xa
xb
xc
2
64
3
75
¼
cosðyeÞ sinðyeÞ
cosðye2p=3Þ sinðye2p=3Þ
cosðye þ 2p=3Þ sinðye þ 2p=3Þ
2
64
3
75
xd
xq
#
ð11Þ
where ye is theanglepositionbetweenthe d-axis ofthesynchronouslyrotatingandthe
stationaryreferenceframes,andthequantitiesareassumedtobebalanced.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 304

6. Using thefield-orientationcontrolprinciple [3] the currentcomponent ids
e is alignedin
the directionoftherotorfluxvector cr, andthecurrentcomponent iqs
e is alignedinthe
directionperpendiculartoit.Undertheseconditions,itissatisfiedthat
ce
qr ¼ 0; ce
dr ¼ jcrj ð12Þ
Fig. 1 shows thevectorialdiagramoftheinductionmotorinthestationaryandinthe
synchronouslyrotatingreferenceframes.Thesubscripts‘s’indicatesthestationaryframe
and thesubscript‘e’indicatesthesynchronouslyrotatingreferenceframe.
Therefore,takingintoaccountthepreviousresults,theequationofinductionmotor
torque (10)issimplifiedto
Te ¼
3p
4
Lm
Lr
ce
drie
qs ¼ KT ie
qs ð13Þ
wherethetorqueconstant, KT, isdefinedasfollows:
KT ¼
3p
4
Lm
Lr
ce
dr ð14Þ
ce
dr being thecommandrotorflux.
With theabove-mentionedfieldorientation,thedynamicsoftherotorfluxisgivenby [3]
dce
dr
dt
þ
ce
dr
Tr
¼
Lm
Tr
ie
ds ð15Þ
Then, themechanicalequation(9)becomes
w_ m þ awm þ f ¼ bie
qs ð16Þ
Fig. 1.Vectorialdiagramoftheinductionmotor.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 305

7. where theparametersaredefinedas
a ¼
B
J
; b ¼
KT
J
; f ¼
TL
J
ð17Þ
Now,wearegoingtoconsiderthepreviousmechanicalequation(16)withuncertainties
as follows:
w_ m ¼ ða þ DaÞwmðf þ DfÞ þ ðb þ DbÞie
qs ð18Þ
where theterms Da, Db and Df representtheuncertaintiesoftheterms a, b and f
respectively.Itshouldbenotedthattheseuncertaintiesareunknown,andthattheprecise
calculationofanupperboundis,ingeneral,ratherdifficulttoachieve.
Let usdefinethetrackingspeederrorasfollows:
eðtÞ ¼ wmðtÞw
mðtÞ ð19Þ
where wm
n is therotorspeedcommand.
Takingthederivativeofthepreviousequationwithrespecttotimeyields
e_ðtÞ ¼ w_ mw_
m ¼ aeðtÞ þ uðtÞ þ dðtÞ ð20Þ
where thefollowingtermshavebeencollectedinthesignal u(t):
uðtÞ ¼ bie
qsðtÞaw
mðtÞf ðtÞw_
mðtÞ ð21Þ
and theuncertaintytermshavebeencollectedinthesignal d(t),
dðtÞ ¼ DawmðtÞDf ðtÞ þ Dbie
qsðtÞ ð22Þ
To compensatefortheabovedescribeduncertaintiespresentinthesystem,asliding
adaptivecontrolschemeisproposed.Intheslidingcontroltheory,theswitchinggainmust
be constructedsoastoattaintheslidingcondition [20,30]. Inordertomeetthisconditiona
suitable choiceoftheslidinggainshouldbemadetocompensatefortheuncertainties.To
select theslidinggainvector,anupperboundoftheparametervariations,unmodelled
dynamics,noisemagnitudes,etc.shouldbegiven,butinpracticalapplicationsthereare
situationsinwhichtheseboundsareunknown,oratleastdifficulttocalculate.Asolution
could betochooseasufficientlyhighvaluefortheslidinggain,butthisapproachcould
cause atoohighcontrolsignal,oratleastmorecontrolactivitythanneededinorderto
achieve thecontrolobjective.
One possiblewaytoovercomethisdifficultyistoestimatethegainandtoupdateitby
means ofsomeadaptationlaw,sothattheslidingconditionisachieved.
Now,wearegoingtoproposetheslidingvariable S(t) withanintegralcomponentas
SðtÞ ¼ eðtÞ þ
Z t
0
ða þ kÞeðtÞ dt ð23Þ
where k is aconstantgain,and a is aparameterthatwasalreadydefinedinEq.(17).
Then theslidingsurfaceisdefinedas
SðtÞ ¼ eðtÞ þ
Z t
0
ða þ kÞeðtÞ dt ¼ 0 ð24Þ
Now, wearegoingtodesignavariablestructurespeedcontroller,thatincorporatesan
adaptiveslidinggain,inordertocontroltheACmotordrive
uðtÞ ¼ keðtÞ^b
ðtÞg sgnðSÞ ð25Þ
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 306

8. wherethe k is thegaindefinedpreviously, ^b
is theestimatedswitchinggain, g is apositive
constant, S is theslidingvariabledefinedinEq.(23)andsgnðÞ is thesignfunction.
The switchinggain ^b
is adaptedaccordingtothefollowingupdatinglaw:
_^b
¼ gjSj; ^b
ð0Þ ¼ 0 ð26Þ
where g is apositiveconstantthatletuschoosetheadaptationspeedfortheslidinggain.
In ordertoobtainthespeedtrajectorytracking,thefollowingassumptionsshouldbe
formulated:
ðA1Þ The gain k must bechosensothattheterm(aþk) isstrictlypositive.Thereforethe
constant k should be k4a.
ðA2Þ Thereexitsanunknownfinitenon-negativeswitchinggain b such that
b4dmax þ Z; Z40
where dmaxZjdðtÞj 8t and Z is apositiveconstant.
Note thatthisconditiononlyimpliesthattheuncertaintiesofthesystemarebounded
magnitudes.
ðA3Þ The constant g must bechosensothat gZ1.
Theorem 1. Consider theinductionmotorgivenbyEq. (18). Then, if assumptions ðA1Þ–ðA3Þ
are verified, the controllaw (25) leads therotormechanicalspeedwm(t) so thatthespeed
trackingerrore(t)=wm(t)wm
n (t) tends tozeroasthetimetendstoinfinity.
The proofofthistheoremwillbecarriedoutusingtheLyapunovstabilitytheory.
Proof. Define theLyapunovfunctioncandidate:
VðtÞ ¼
1
2
SðtÞSðtÞ þ
1
2
~b
ðtÞ~b
ðtÞ ð27Þ
where S(t) istheslidingvariabledefinedpreviouslyand ~b
ðtÞ ¼ ^b
ðtÞb
Its timederivativeiscalculatedas
_V
ðtÞ ¼ SðtÞ_S
ðtÞ þ ~b
ðtÞ
_~b
ðtÞ
¼ S½_e þ ða þ kÞe þ ~b
ðtÞ
_^b
ðtÞ
¼ S½ðae þ u þ dÞ þ ðke þ aeÞ þ ~bgjSj
¼ S½u þ d þ ke þ ð^b
bÞgjSj
¼ S½ke^bgsgnðSÞ þ d þ ke þ ð^b
bÞgjSj
¼ S½d^ bgsgnðSÞ þ ^bgjSjbgjSj
¼ dS^ bgjSj þ ^ bgjSjbgjSj ð28Þ
rjdjjSjbgjSj
rjdjjSjðdmax þ ZÞgjSj
¼ jdjjSjdmaxgjSjZgjSj
rZgjSj ð29Þ
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 307

9. then
_V
ðtÞr0 ð30Þ
It shouldbenotedthatEqs.(23),(20),(25)and(26),andtheassumptions ðA2Þ and ðA3Þ
have beenusedintheproof.
UsingLyapunov’sdirectmethod,since V(t) isclearlypositive-definite, _V
ðtÞ is negative
semidefiniteand V(t) tendstoinfinityas S(t) and ~b
ðtÞ tends toinfinity,thentheequilibrium
at theorigin ½SðtÞ; ~b
ðtÞ ¼½0; 0 is globallystable,andthereforethevariables S(t) and ~b
ðtÞ
are bounded.Then,since S(t) isboundedonehasthat e(t) isalsobounded.
Besides,computingthederivativeofEq.(23),itisobtained:
_S
ðtÞ ¼ _eðtÞ þ ða þ kÞeðtÞ ð31Þ
then, substitutingEq.(20)inEq.(31),
_S
ðtÞ ¼ aeðtÞ þ uðtÞ þ dðtÞ þ ða þ kÞeðtÞ
¼ keðtÞ þ dðtÞ þ uðtÞ ð32Þ
FromEq.(32)wecanconcludethat _S
ðtÞ is boundedbecause e(t), u(t) and d(t) are
bounded.
Now,fromEq.(28)itisdeducedthat
€V
ðtÞ ¼ d_S
ðtÞbg
d
dt
jSðtÞj ð33Þ
which isaboundedquantitybecause _S
ðtÞ is bounded.
Undertheseconditions,since €V
is bounded, _V
is auniformlycontinuousfunction,so
Barbalat’slemmaletusconcludethat _V
-0 as t-1, whichimpliesthat SðtÞ-0 as t-1.
Therefore S(t) tendstozeroasthetime t tendstoinfinity.Moreover,alltrajectories
startingofftheslidingsurface S=0 mustreachitasymptoticallyandthenwillremainonthis
surface.Thissystem’sbehavior,onceontheslidingsurfaceisusuallycalled slidingmode [20].
Whentheslidingmodeoccursontheslidingsurface(24),then SðtÞ ¼ _S
ðtÞ ¼ 0, and
therefore thedynamicbehaviorofthetrackingproblem(20)isequivalentlygovernedby
the followingequation:
_S
ðtÞ ¼ 0 ) _eðtÞ ¼ ða þ kÞeðtÞ ð34Þ
Then, underassumption ðA1Þ, thetrackingerror e(t) convergestozeroexponentially.
It shouldbenotedthat,atypicalmotionundersliding-modecontrolconsistsofa reaching
phase duringwhichtrajectoriesstartingofftheslidingsurface S=0 movetowardsitand
reachit,followedbya slidingphase duringwhichthemotionisconfinedtothissurfaceand
wherethesystemtrackingerror,representedbythereduced-ordermodel(34),tendstozero.
Finally,thetorquecurrentcommand, iqs
en(t), canbeobtaineddirectlysubstitutingEq.(25)
in Eq.(21):
ie
qs ðtÞ ¼
1
b
½ke^ bgsgnðSÞ þ aw
m þ w_
m þ f ð35Þ
Therefore,theproposedvariablestructurespeedcontrolwithadaptiveslidinggain
resolves thespeedtrackingproblemfortheinductionmotor,withuncertaintiesin
mechanicalparametersandloadtorque.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 308

10. 4. Simulationresults
In thissectionwewillstudythespeedregulationperformanceoftheproposedadaptive
sliding-modefieldorientedcontrolversusspeedreferenceandloadtorquevariationsby
means ofsimulationexamples.Inparticular,theexamplepresentedconsistofarepre-
sentativespeedreferencetrackingproblem,combinedwithloadtorquevariationsduring
the evolutionoftheexperimentandconsideringacertaindegreeofuncertainty,inorderto
attain acompletescopeofthebehaviorofthesystem.
The blockdiagramoftheproposedrobustcontrolschemeispresentedin Fig. 2.
The block‘VSCcontroller’representstheproposedadaptivesliding-modecontroller,and
it isimplementedbyEqs.(23),(35),and(26).Theblock‘limiter’limitsthecurrentapplied
to themotorwindingssothatitremainswithinthelimitvalue,anditisimplementedbya
saturationfunction.Theblock‘ dqe-abc’ makestheconversionbetweenthesynchro-
nouslyrotatingandstationaryreferenceframes,andisimplementedbyEq.(11).Theblock
‘currentcontroller’consistsofathreehysteresis-bandcurrentPWMcontrol,whichis
basicallyaninstantaneousfeedbackcurrentcontrolmethodofPWMwheretheactual
current(iabc) continuallytracksthecommandcurrent(iabc
n ) withinahysteresisband.The
block‘PWMinverter’isasixIGBT-diodebridgeinverterwith780VDCvoltagesource.
The block‘fieldweakening’givesthefluxcommandbasedonrotorspeed,sothatthePWM
controllerdoesnotsaturate.Theblock‘ids
en calculation’providesthecurrentreference ids
en
fromtherotorfluxreferencethroughEq.(15).Theblock‘wr estimator’representsthe
proposedrotorspeedandsynchronousspeedestimator,anditisimplementedbyEqs.(8)
and (6)respectively.Finally,theblock‘IM’representstheinductionmotor.
The inductionmotorusedinthiscasestudyisa50HP,460V,fourpole,60Hzmotor
having thefollowingparameters: Rs ¼ 0:087 O, Rr ¼ 0:228 O, Ls=35.5 mH, Lr=35.5 mH,
and Lm=34.7 mH.
The systemhasthefollowingmechanicalparameters: J=1.357kgm2 and B=0.05 N
m s.Itisassumedthatthereisanuncertaintyaround20%inthesystemparameters,which
will beovercomebytheproposedslidingcontrol.
The followingvalueshavebeenchosenforthecontrollerparameters: k=45 and g ¼ 30.
In thisexamplethemotorstartsfromastandstillstateandwewanttherotorspeedto
follow aspeedcommandthatstartsfromzeroandacceleratesuntiltherotorspeedis
Fig. 2.Blockdiagramoftheproposedadaptivesliding-modecontrol.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 309

11. 100 rad/s,thentherotorspeedismaintainedconstantandafter,attime1.3s,therotor
deceleratesuntiltherotorspeedis80rad/s.Inthissimulationexample,thesystemstarts
with aninitialloadtorque TL=0 Nmandattime t=2.3 stheloadtorquestepsfrom
TL=0 to200Nm,andasbefore,itisassumedthatthereisanuncertaintyaround20%in
the loadtorque.
Fig. 3 shows thedesiredrotorspeed(dashedline)andtherealrotorspeed(solidline).
As itmaybeobserved,afteratransitorytimeinwhichtheslidinggainisadapted,therotor
speed tracksthedesiredspeedinspiteofsystemuncertainties.However,attime t=2.3 sa
small speederrorcanbeobserved.Thiserrorappearsbecauseatorqueincrementoccursat
this time,sothatthecontrolsystemlosestheso-called‘slidingmode’becausetheactual
sliding gainistoosmallinordertoovercomethenewuncertaintyintroducedinthesystem
due tothenewtorque.Butthen,afterashorttimetheslidinggainisadaptedonceagainso
that thisgaincancompensateforthesystemuncertaintieswhicheliminatestherotor
speed error.
Fig. 4 presentsthetimeevolutionoftheestimatedslidinggain.Theslidinggainstarts
from zeroandthenitisincreaseduntilitsvalueishighenoughtocompensateforthe
system uncertainties.Besides,theslidingremainsconstantbecausethesystemuncertainties
remain constantaswell.Later,attime2.3s,thereisanincrementinthesystem
uncertaintiescausedbytheincrementintheloadtorque.Therefore,theslidingshouldbe
adapted onceagaininordertoovercomethenewsystemuncertainties.Asitcanbeseenin
the figureaftertheslidinggainisadapted,itremainsconstantagain,sincethesystem
uncertaintiesremainconstantaswell.
It shouldbenotedthattheadaptiveslidinggainallowstoemployasmallerslidinggain,
so thatthevalueoftheslidinggaindonothavetobechosenhighenoughtocompensate
for allpossiblesystemuncertainties,becausewiththeproposedadaptiveschemethesliding
gain isadapted(ifitisnecessary)whenanewuncertaintyappearsinthesysteminorderto
surmount thisuncertainty.
Fig. 5 shows thetimeevolutionoftheslidingvariable.Inthisfigureitcanbeseenthat
the systemreachtheslidingcondition(S(t)=0) attime t=0.13 s,butthenthesystemloses
0 0.511.522.53
0
20
40
60
80
100
120
Time (s)
Rotor Speed (rad/s)
wm *
wm
Fig. 3.Referenceandrealrotorspeedsignals(wm
n , wm).
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 310

12. this conditionattime t=2.3 sduetothetorqueincrementwhich,inturn,producesan
incrementinthesystemuncertaintiesthatcannotbecompensatedbytheactualvalueof
the slidinggain.However,afteratransitorytimeinwhichtheslidinggainisadaptedin
order tocompensatethenewsystemuncertainty,thesystemreachesthesliding
conditionagain.
Fig. 6 showsthecurrentofonestatorwinding.Thisfigureshowsthatintheinitialstate,
the currentsignalpresentsahighvaluebecauseahightorqueisnecessarytoincrementthe
rotor speedduetotherotorinertia.Then,intheconstant-speedregion,themotortorque
only hastocompensatethefrictionandtherefore,thecurrentislower.Finally,attime
t=2.3 sthecurrentincreasesbecausetheloadtorquehasbeenincreased.
0 0.511.522.53
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
Time (s)
Sliding Variable
Fig. 5.Slidingvariable.
0 0.511.522.53
0
2
4
6
8
10
12
14
Time (s)
Sliding Gain
Fig. 4.Estimatedslidinggain ð^b
Þ.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 311

13. Fig. 7 shows themotortorque.Asinthecaseofthecurrent(Fig. 6), themotortorque
has ahighinitialvalueinthespeedaccelerationzoneandthenthevaluedecreasesina
constant region.Later,attime t=1.3 s,themotortorquedecreasesagaininorderto
reduce therotorspeed.Finally,attime t=2.3 sthemotortorqueincreasesinorderto
compensatetheloadtorqueincrement.Inthisfigureitmaybeseenthatinthemotor
torque appearstheso-calledchatteringphenomenon,howeverthishighfrequencychanges
in thetorquewillbefilteredbythemechanicalsysteminertia.
5. Conclusions
In thispapersensorlessrobustvectorcontrolforinductionmotordriveswithan
adaptivevariablesliding-modevectorcontrollawhasbeenpresented.Therotorspeed
0 0.511.522.53
−500
−400
−300
−200
−100
0
100
200
300
400
500
Time (s)
Stator Current
Fig. 6.Statorcurrent(isa).
0 0.511.522.53
−100
−50
0
50
100
150
200
250
300
Motor Torque (N)
Time (s)
Fig. 7.Motortorque(Te).
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 312

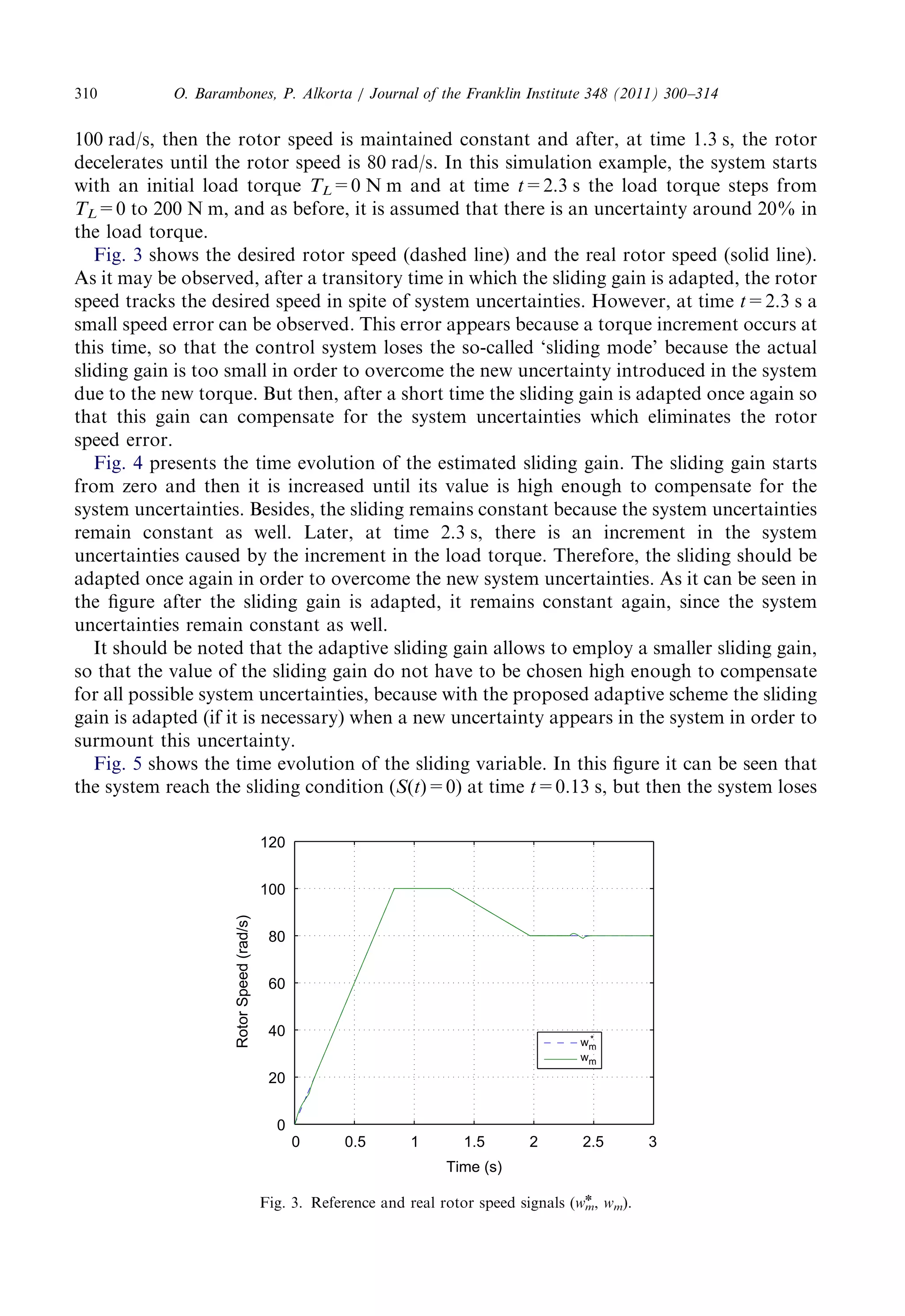
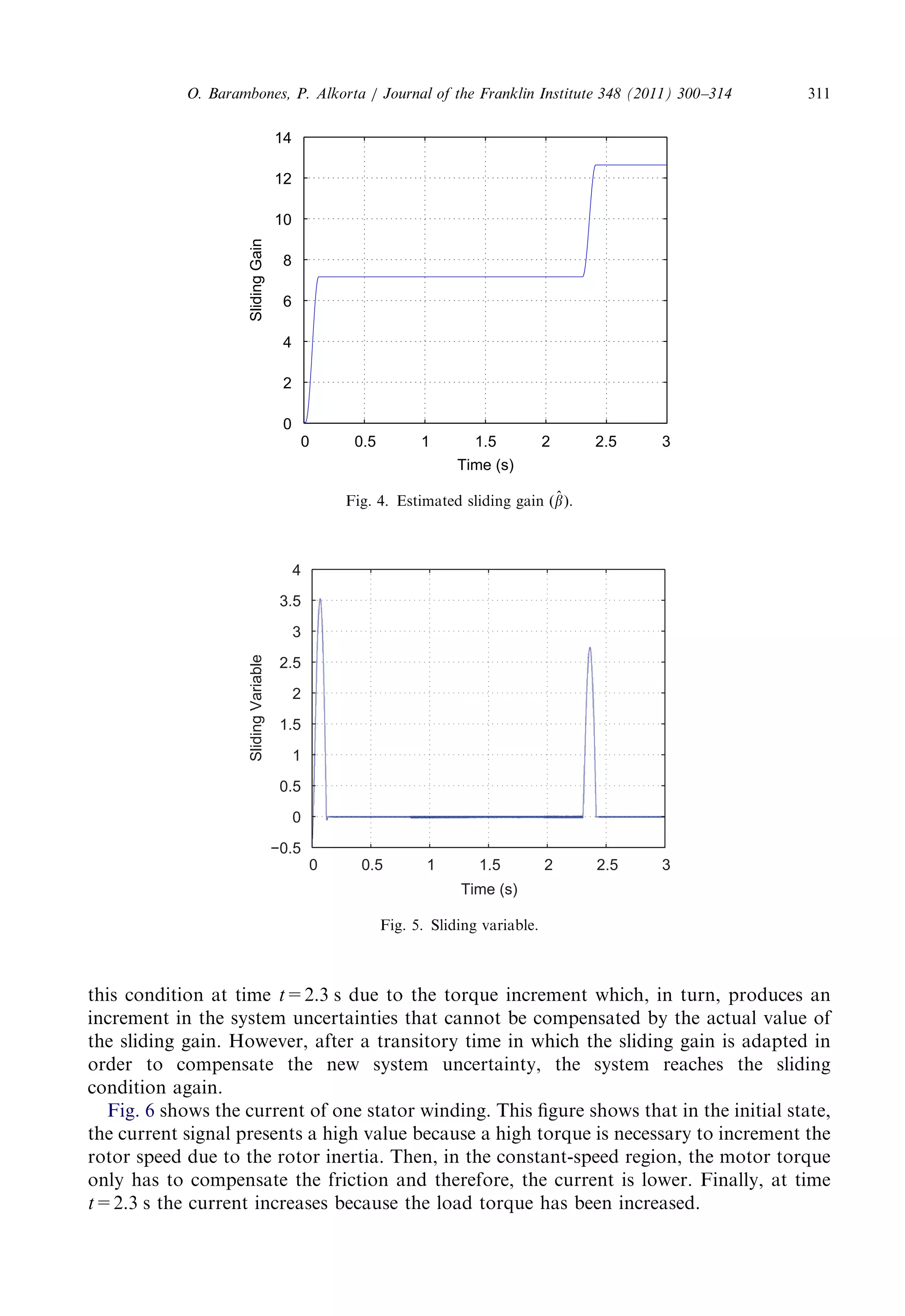
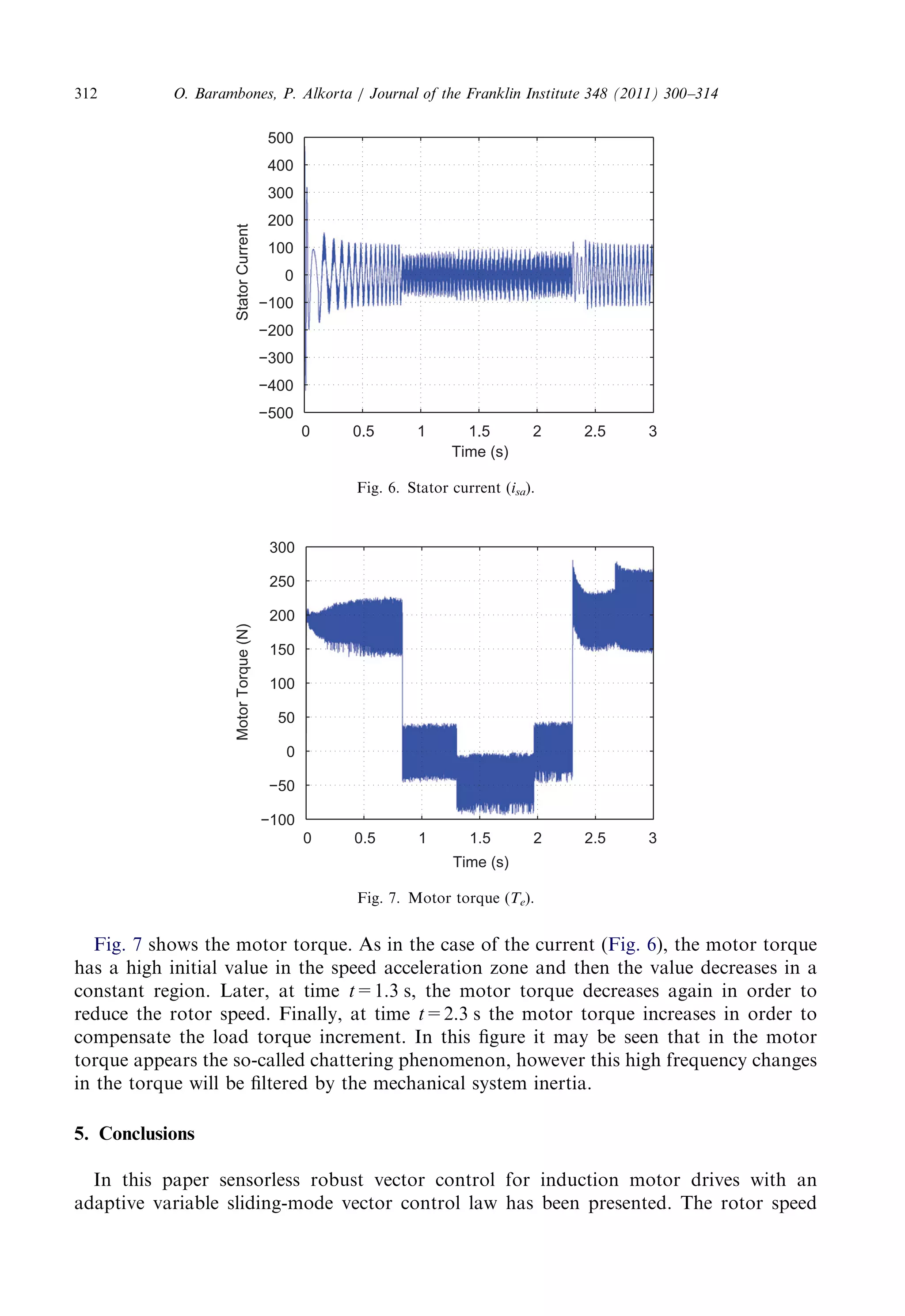
14. estimatorisbasedonstatorvoltageequationsandrotorfluxequationsinthestationary
referenceframe.Itisproposedasavariablestructurecontrolwhichusesanintegralsliding
surfacetorelaxtherequirementoftheaccelerationsignal,thatisusualinconventional
sliding-modespeedcontroltechniques.Duetothenatureoftheslidingcontrolthiscontrol
scheme isrobustunderuncertaintiescausedbyparametererrorsorbychangesintheload
torque. Moreover,theproposedvariablestructurecontrolincorporatesandadaptive
algorithmtocalculatetheslidinggainvalue.Theadaptationoftheslidinggain,ontheone
hand avoidstheneedofcomputingtheupperboundofthesystemuncertainties,andon
the otherhandallowstoemployassmallerslidinggainaspossibletoovercometheactual
system uncertainties.Thenthecontrolsignalofourproposedvariablestructurecontrol
schemes willbesmallerthanthecontrolsignalsofthetraditionalvariablestructurecontrol
schemes,becauseinthesetraditionalschemestheslidinggainvalueshouldbechosenhigh
enoughtoovercomeallthepossibleuncertaintiesthatcouldappearinthesystemalong
the time.
The closedloopstabilityofthedesignpresentedinthispaperhasbeenprovedthought
Lyapunovstabilitytheory.Finally,bymeansofsimulationexamples,ithasbeenshown
that theproposedcontrolschemeperformsreasonablywellinpractice,andthatthespeed
trackingobjectiveisachievedunderuncertaintiesintheparametersandloadtorque.
Acknowledgments
The authorsareverygratefultotheBasqueGovernmentbythesupportofthiswork
through theprojectS-PE09UN12andtotheUPV/EHUbyitssupportthroughproject
GUI07/08.
References
[1] W.Leonhard,ControlofElectricalDrives,Springer,Berlin,1996.
[2] P.Vas,VectorControlofACMachines,OxfordSciencePublications,Oxford,1994.
[3] B.K.Bose,ModernPowerElectronicsandACDrives,PrenticeHall,NewJersey,2001.
[4] R.Beguenane,M.A.Ouhrouche,A.M.Trzynadlowski,Anewschemeforsensorlessinductionmotorcontrol
drives operatinginlowspeedregion,MathematicsandComputersinSimulation71(2006)109–120.
[5] S.Sunter,Slipenergyrecoveryofarotor-sidefieldorientedcontrolledwoundrotorinductionmotorfedby
matrix converter,JournaloftheFranklinInstitute345(2008)419–435.
[6] M.Comanescu,Aninduction-motorspeedestimatorbasedonintegralsliding-modecurrentcontrol,IEEE
Transactions onIndustrialElectronics56(9)(2009)3414–3423.
[7] M.I.Marei,M.F.Shaaban,A.A.El-Sattar,Aspeedestimationunitforinductionmotorsbasedonadaptive
linear combiner,EnergyConversionandManagement50(2009)1664–1670.
[8] A.Y.Alanis,E.N.Sanchez,A.G.Loukianov,E.A.Hernandez,Discrete-timerecurrenthighorderneural
networks fornonlinearidentification,JournaloftheFranklinInstitute347(2010)1253–1265.
[9] T-J.Ren,T-C.Chen,Robustspeed-controlledinductionmotordrivebasedonrecurrentneuralnetwork,
Electric PowerSystemResearch76(2006)1064–1074.
[10] M.Montanari,S.Peresada,A.Tilli,Aspeed-sensorlessindirectfield-orientedcontrolforinductionmotors
based onhighgainspeedestimation,Automatica42(2006)1637–1650.
[11] R.Marino,P.Tomei,C.M.Verrelli,Anadaptivetrackingcontrolfromcurrentmeasurementsforinduction
motors withuncertainloadtorqueandrotorresistance,Automatica44(2008)2593–2599.
[12] J.B.Oliveira,A.D.Araujo,S.M.Dias,Controllingthespeedofathree-phaseinductionmotorusinga
simplified indirectadaptiveslidingmodescheme,ControlEngineeringPractice18(2010)577–584.
[13] M.A.Fnaiech,F.Betin,G.A.Capolino,F.Fnaiech,Fuzzylogicandsliding-modecontrolsappliedtosix-
phase inductionmachinewithopenphases,IEEETransactionsonIndustrialElectronics57(1)(2010)
354–364.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 313

15. [14] M.Montazeri-Gh,A.Poursamad,B.Ghalichi,Applicationofgeneticalgorithmforoptimizationofcontrol
strategy inparallelhybridelectricvehicles,JournaloftheFranklinInstitute343(2006)420–435.
[15] A.Benchaib,C.Edwards,Nonlinearslidingmodecontrolofaninductionmotor,InternationalJournalof
Adaptive ControlandSignalProcesing14(2000)201–221.
[16] O.Barambones,A.J.Garrido,Asensorlessvariablestructurecontrolofinductionmotordrives,Electric
Power SystemsResearch72(2004)21–32.
[17] R.Yazdanpanah,J.Soltani,G.R.ArabMarkadeh,Nonlineartorqueandstatorfluxcontrollerforinduction
motor drivebasedonadaptiveinput–outputfeedbacklinearizationandslidingmodecontrol,Energy
ConversionandManagement49(2008)541–550.
[18] B.Castillo-Toledo,S.DiGennaro,A.G.Loukianov,J.Rivera,Discretetimeslidingmodecontrolwith
applicationtoinductionmotors,Automatica44(2008)3036–3045.
[19] T.Orowska-Kowalska,M.Kami nski, K.Szabat,Implementationofasliding-modecontrollerwithan
integral functionandfuzzygainvaluefortheelectricaldrivewithanelasticjoint,IEEETransactionson
Industrial Electronics57(4)(2010)1309–1317.
[20] V.I.Utkin,Slidingmodecontroldesignprinciplesandapplicationstoelectricdrives,IEEETransactionson
Industrial Electronics40(1993)26–36.
[21] H.Yang,Y.Xia,P.Shi,Observer-basedslidingmodecontrolforaclassofdiscretesystemsviadelta
operator approach,JournaloftheFranklinInstitute347(2010)1199–1213.
[22] I.Boiko,Frequencydomainprecisionanalysisanddesignofslidingmodeobservers,JournaloftheFranklin
Institute 347(2010)899–909.
[23] T.Furuhashi,S.Sangwongwanich,S.Okuma,Aposition-and-velocitysensorlesscontrolforbrushlessDC
motors usinganadaptiveslidingmodeobserver,IEEETransactionsonIndustrialElectronics39(1992)
89–95.
[24] A.B.Proca,A.Keyhani,J.M.Miller,Sensorlesssliding-modecontrolofinductionmotorsusingoperating
condition dependentmodels,IEEETransactionsonEnergyConversion18(2003)205–212.
[25] G.Bartolini,A.Pisano,E.Punta,E.Usai,Asurveyofapplicationsofsecond-orderslidingmodecontrolto
mechanicalsystems,InternationalJournalofControl76(2003)875–892.
[26] M.Rashed,K.B.Goh,M.W.Dunnigan,P.F.A.MacConnell,A.F.Stronach,B.W.Williams,Sensorless
second-ordersliding-modespeedcontrolofavoltage-fedinduction-motordriveusingnonlinearstate
feedback, IEEProceedingsElectricPowerApplications152(2005)1127–1136.
[27] C.Aurora,A.Ferrara,Aslidingmodeobserverforsensorlessinductionmotorspeedregulation,
InternationalJournalofSystemsScience38(2007)913–929.
[28] Y.Xia,Z.Zhu,C.Li,H.Yang,Q.Zhu,Robustadaptiveslidingmodecontrolforuncertaindiscrete-time
systems withtimedelay,JournaloftheFranklinInstitute347(1)(2010)339–357.
[29] M.C.Pai,Designofadaptiveslidingmodecontrollerforrobusttrackingandmodelfollowing,Journalofthe
Franklin Institute347(2010)1838–1849.
[30] J.J.E.Slotine,W.Li,AppliedNonlinearControl,Prentice-Hall,EnglewoodCliffs,NJ,USA,1991.
O. Barambones,P.Alkorta/JournaloftheFranklinInstitute348(2011)300–314 314